箱梁涡振的缩尺效应及振幅修正研究
2021-09-26陈星宇徐昕宇曾永平郑晓龙李永乐
陈星宇,徐昕宇,曾永平,郑晓龙,李永乐
(1.中铁二院工程集团有限责任公司,成都 610031; 2.西南交通大学桥梁工程系,成都 610031)
流线形箱梁具有外形优美、受力明确、颤振稳定性好等优点,已被广泛应用于国内外大跨度桥梁中,目前,我国已建或在建的主跨超过800 m悬索桥也多为流线形箱梁形式。但流线形箱梁的涡振稳定性能较差,如Rio-Niteroi Bridge[1]、Great Belt Bridge[2]、椒江二桥[3]等都曾出现过涡激共振灾害。尽管涡振不会像颤振或驰振那样引起桥梁结构的毁灭性破坏,但涡振的起振风速低、出现概率大,影响桥上行车和行人舒适性[4-5],还可能引起桥梁结构的疲劳性破坏,危害结构安全。
自1940年Tacoma Narrows Bridge风毁事故发生后,桥梁抗风研究得到更多的重视,取得了大量可应用于实际工程的成果,桥梁抗风理论也逐步建立,但到目前为止,尚未能通过理论分析方法得到普遍适用的桥梁涡振解析解[6],风洞试验方法仍然是桥梁涡振研究中最为常用的研究手段[7-14]。风洞实验室空间有限,目前,世界最大边界层风洞(XNJD-3风洞)的高度仅为4.5 m,其余大多数边界层风洞的高度不足3 m。已有研究表明,桥梁断面高度与风洞高度之比(阻塞比)不宜超过5%,建议将其控制在2.5%以内[15]。在风洞试验中,对桥梁结构某些细小构件周围流场的模拟可能与实际情况存在很大差别,且此时缩尺模型风洞试验的雷诺数往往远小于实际桥梁,因此,试验结果可能存在较大误差。现有关于雷诺数效应的研究较为常见,但直接针对风洞试验中桥梁涡振缩尺效应的研究较少,缩尺比对流线形箱梁涡振试验结果的影响尚不明确。
随着计算机性能的飞速提升,数值模拟技术日趋成熟,因其可重复性、可视化及省时省力等优点被广泛应用于桥梁风工程研究中。周帅等[16]对吊杆的软驰振现象进行了数值模拟,模拟结果与试验结果吻合良好。徐枫等[17]采用数值模拟方法研究了不同形状柱体的涡振性能,并验证了模拟结果的可靠性。唐浩俊等[18-21]对桁梁、塔柱等结构进行了颤振和涡振数值模拟计算,验证了数值模拟计算结果。陈星宇等[22-23]对扁平箱梁的涡振性能开展数值模拟研究,基于风洞试验结果对比验证了数值模拟计算结果的准确性。
基于上述原因,以流线形箱梁为研究对象,采用数值模拟方法,建立与风洞边界条件相近的二维数值模型,通过修改尺寸放缩比例,开展不同缩尺比的箱梁竖向涡振研究,提出常见缩尺比对应的涡振振幅修正公式。
1 数值模拟分析模型
1.1 涡振数值模拟的实现
当结构发生涡振时,其竖向振动的结构动力学微分方程可表述为
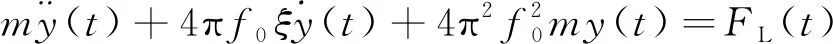
(1)
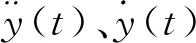
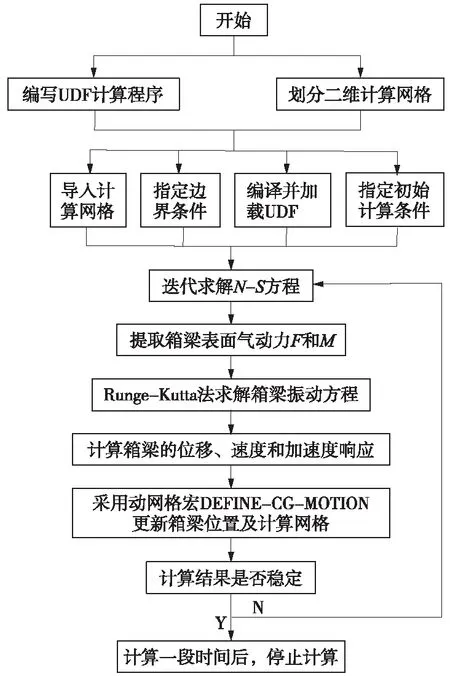
图1 涡振数值模拟计算流程
1.2 数值模型
以某大跨度悬索桥箱梁为研究对象,该箱梁的断面形式如图2(a)所示,B为箱梁宽度;D为箱梁高度(不计附属设施高度);θ为风嘴角度,取θ=45°。
图2(b)展示了模型计算域、边界条件等。计算域为长方形,在垂直来流和平行来流方向上的长度分别为40D和19B。已有研究表明,该箱梁仅在5°攻角下出现涡激共振现象[2],为保证与试验条件相同,也将该箱梁顺时针旋转5°,并将其设置为无滑移壁面边界,上下边界也定义为不透风的壁面边界,将左侧定义为速度入口,右侧设置为压力出口。为保证数值模拟精度并同时兼顾计算效率,将计算域划分为刚体区域、动网格区域及外部区域三类。刚体区域为包含箱梁在内的矩形区域,与箱梁共同运动,区域内网格划分极为细密以保证箱梁表面附近流场的准确模拟,该区域的长和高分别为1.12B和1.25D。为满足动网格技术需要,动网格区域内划分为三角形网格。动网格区域外的其余区域即为外部区域,由于距箱梁相对较远,该区域内均为尺寸稍大的结构化网格。
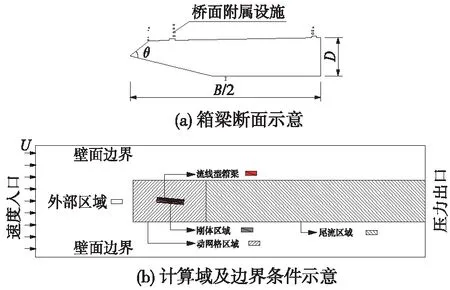
图2 计算区域示意
文献[22-23]针对文中采用数值模型的网格无关性和步长无关性等进行了详细的验证,最终建立的数值模型中,计算域内网格的总数为279 031个,壁面各处Y+值均小于1,数值模拟时间步长取为0.000 445 s。数值模拟中湍流模型等参数设置及模拟结果可靠性验证参考文献[22]。
2 涡激振动的缩尺效应
2.1 计算工况
为研究箱梁涡振风洞试验中缩尺效应对试验结果的影响,分别针对1:1的实桥尺寸及3种风洞试验常用缩尺比下的箱梁断面开展了数值模拟计算。其中,1:20缩尺比多对应于大比尺节段模型,1:50缩尺比往往用于常规节段模型试验中,1:100缩尺比常用于全桥气弹模型试验。基于上节建立的数值模型,将箱梁断面和计算域同时放缩相应倍数,即可得到对应缩尺比下的数值计算模型。在数值模拟计算中,不同缩尺比下箱梁断面的主要参数见表1。
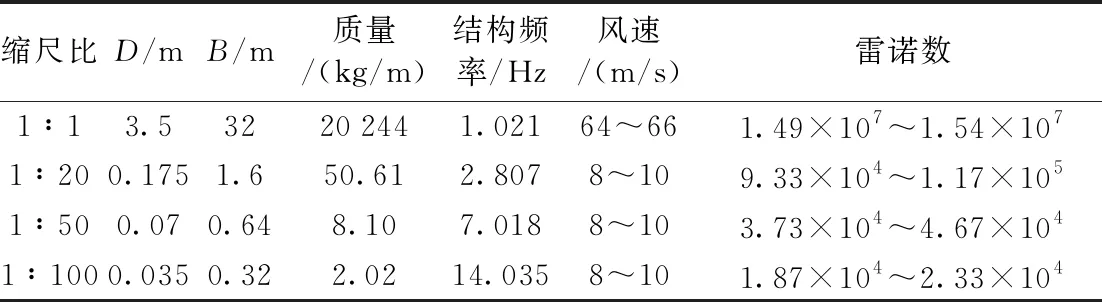
表1 不同缩尺比下箱梁断面的主要计算参数
2.2 静止状态下静力三分力的缩尺效应
如图3所示,在速度为U的流体中,箱梁断面受到阻力FD、升力FL以及力矩M的作用。在风轴坐标系下,阻力系数和升力系数分别为

图3 作用在箱梁上的静力三分力
(2)
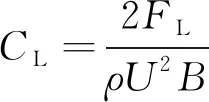
(3)
式中,ρ为空气密度;U为来流平均风速;D和B分别为箱梁的高度和宽度。
不同缩尺比下箱梁气动力系数随攻角的变化曲线如图4所示,不同攻角下气动力系数随缩尺比变化的最大变化率列于表2中。
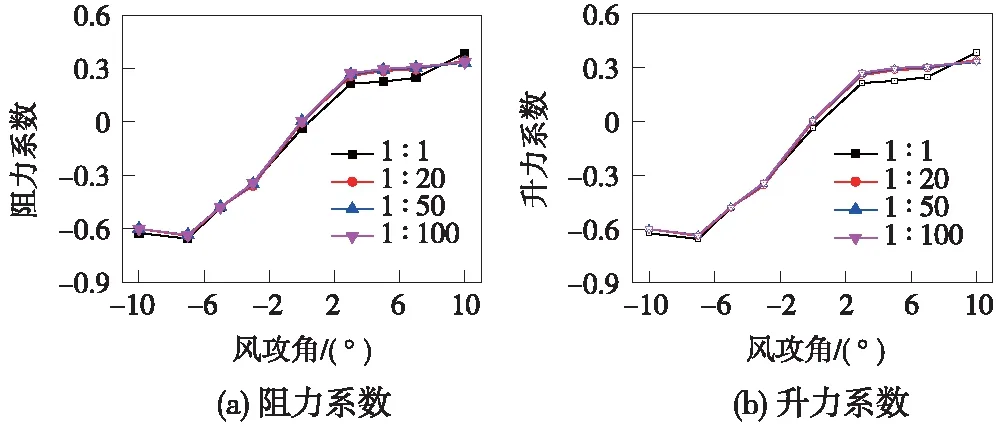
图4 不同缩尺比下箱梁的气动力系数
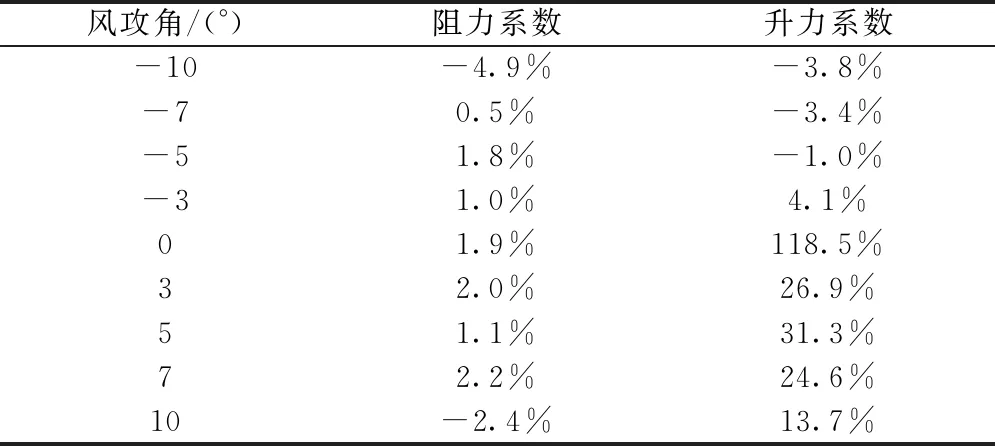
表2 不同攻角下气动力系数随缩尺比变化的最大变化率
由图4及表2可以看出,在0°~8°攻角范围内,缩尺比越小,阻力系数和升力系数越大;随着攻角的继续增大,当攻角超过9°后,缩尺比越小,阻力系数和升力系数越小;在负攻角下,不同缩尺比下三分力系数变化幅度不大。在-10°~10°风攻角范围内,缩尺比改变后,阻力系数的变化幅度在5%以内;而对于升力系数,在0°攻角下其变化幅度超过100%,这是由于此时箱梁的升力系数接近于0,升力系数小幅变化也会引起极大的变化率,而在负攻角下,升力系数的变化率在5%以内,但在正攻角下变化幅度最大达到31.1%。
2.3 涡振状态下动态升力的缩尺效应
图5给出了不同缩尺比下的动态升力时程及频谱。由图5可见,不同缩尺比下箱梁涡振时的动态升力存在显著不同,缩尺比越大,升力系数的峰值越大,振动幅值也更大;1∶20缩尺比下的动态升力明显大于较小缩尺比;1∶50缩尺比下的动态升力略大于1∶100缩尺比。各缩尺比下动态升力的振动频率存在显著差异,这是因为不同缩尺比的箱梁固有频率各不相同。此外,将不同缩尺比情况下的动态升力时程进行傅里叶变换后对比分析,可以发现,缩尺比越大,前四阶频率贡献的能量越大。
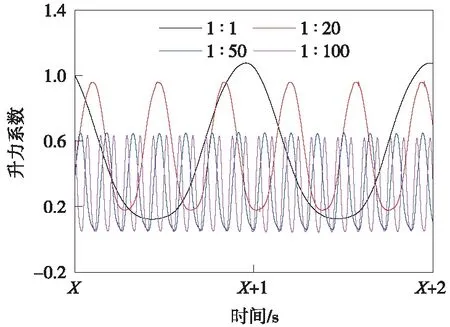
图5 不同缩尺比下的动态升力时程
2.4 涡振振幅的缩尺效应
图6给出了各缩尺比下涡振响应随风速的变化曲线,图6中,涡振振幅和风速分别通过ymax/D和U/fD进行无量纲化处理。由图6可见,不同缩尺比大小的涡振最大振幅出现的风速相近,但缩尺比大小对箱梁涡振振幅影响较大,尤其是1∶1、1∶20和1∶50三种缩尺比下涡振振幅变化较大,1∶50和1∶100缩尺比下的涡振振幅差异相对较小。
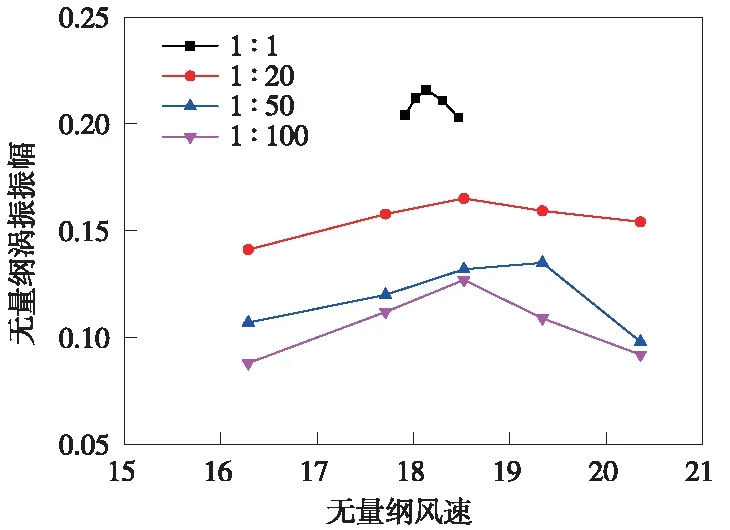
图6 不同缩尺比下箱梁的涡振振幅-风速变化曲线
不同缩尺比下箱梁涡振位移时程及振幅如图7所示,无量纲位移通过涡振位移与箱梁高度之比y/D表示。通过对比不同缩尺比时涡振响应时程可以发现,箱梁从静止发展至稳定振动所需时间随着缩尺比的增大而增大,这是由于涡振需要经历自激、自限幅直至稳定振动的过程,对于本次研究对象而言,涡振由静止发展至稳定大约需40个周期,不同缩尺比时结构频率存在差异,振动一个周期所需时间随缩尺比增大而增大。
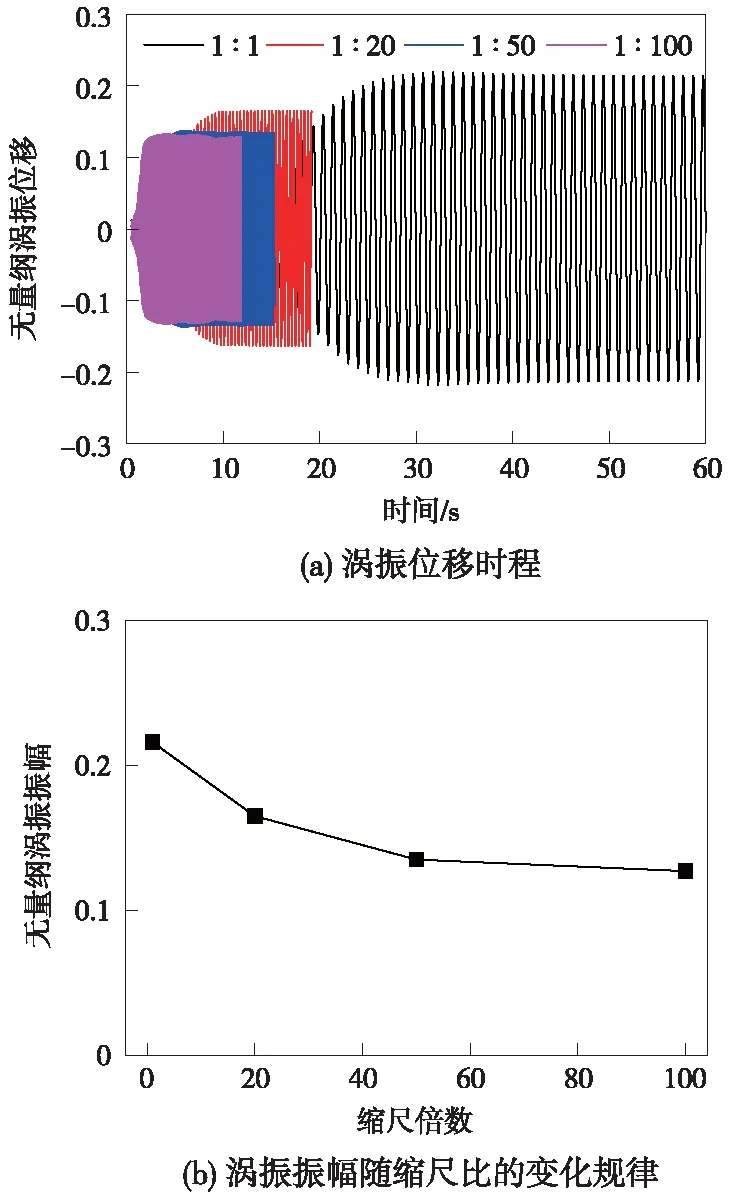
图7 不同缩尺比下的涡振响应
表3列出了不同缩尺比下箱梁涡振的数值模拟结果。首先,不同缩尺比的箱梁涡振时,箱梁的涡振频率与结构固有频率相近,各缩尺比模型的斯托罗哈数(St数)差异很小。其次,当缩尺比为1∶1,涡振最大位移幅值在无量纲风速为18.1时发生,此时雷诺数为1.51×107,涡振最大振幅为0.216D;当缩尺比为1∶20,涡振最大位移幅值发生在无量纲风速为18.5时,对应的雷诺数为1.06×105,涡振最大振幅为0.165D;当缩尺比为1∶50,涡振最大位移幅值发生在无量纲风速为19.3时,对应雷诺数为4.25×104,涡振最大振幅为0.135D;当缩尺比为1∶100,涡振最大位移幅值在无量纲风速为18.5时发生,此时雷诺数为2.12×104,涡振最大振幅为0.127D。由此可见,缩尺比对箱梁的涡振振幅影响显著,缩尺比越小,涡振振幅越小,相比于缩尺比为1∶1时的涡振最大振幅,缩尺比为1∶20时的最大振幅减小了23.6%,在1∶50缩尺比时则减小了37.5%,缩尺比为1∶100时最大振幅减小了41.2%。
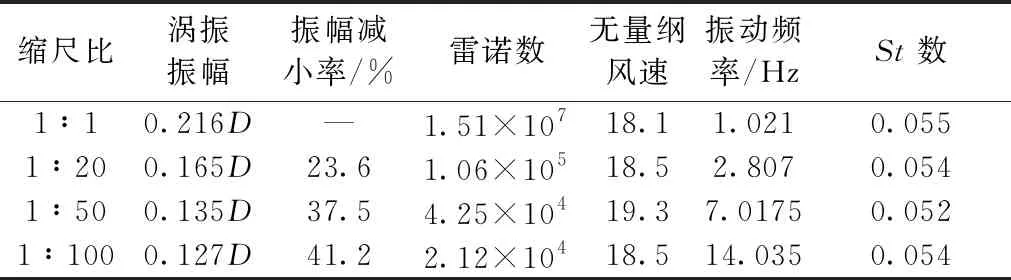
表3 不同缩尺比下箱梁涡振的数值模拟结果
3 涡振振幅修正
缩尺比对箱梁涡振振幅的影响较为明显,随着缩尺比的减小,涡振振幅减小。由此可见,相比于实际尺寸的箱梁而言,小比例尺箱梁模型的涡振风洞试验得到的涡振振幅将偏小,将试验结果直接运用于实际工程中,可能存在不安全因素。因此,有必要对不同缩尺比下的涡振振幅进行修正,使结果更接近于真实情况。
以1∶1缩尺比下涡振振幅为基准,计算各缩尺比下的修正系数,得到了缩尺比修正系数随缩尺比的变化规律,并进行拟合。如图8所示,图中横坐标缩尺倍数为缩尺比中的分母项。图8中涡振振幅的缩尺比修正系数拟合公式如式(4)所示。在箱梁的缩尺模型涡振试验中,试验测得的涡振振幅可乘以式中的缩尺比修正系数,换算为实桥比例尺下的涡振振幅,如式(5)所示。
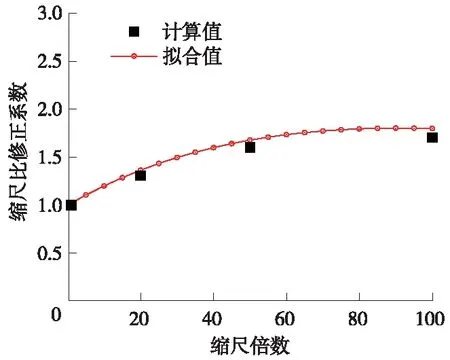
图8 涡振振幅随缩尺倍数变化规律
kSC=2 145e-0.007 996xSC-2 144e-0.008 01xSC
1≤xSC≤100
(4)
(y/D)实桥=kSC·(y/D)SC
(5)
式中,kSC为涡振振幅的缩尺比修正系数;xSC为缩尺倍数。
4 结论
(1)缩尺比的变化对箱梁静力三分力存在一定影响。在0°~8°攻角范围内,缩尺比越小,阻力系数和升力系数越大;当攻角超过9°后,随着攻角继续增大,缩尺比越小,阻力系数和升力系数越小;负攻角时,不同缩尺比下三分力系数变化幅度不大。
(2)缩尺比对箱梁的涡振振幅影响显著,缩尺模型的涡振振幅小于实桥尺寸下的涡振振幅,且缩尺比越小,涡振振幅越小。相比于缩尺比为1∶1时的涡振最大振幅,缩尺比1∶20时的最大振幅减小23.6%,缩尺比1∶50时则减小37.5%,缩尺比1∶100时减小41.2%。
(3)建立了箱梁的涡振振幅缩尺比修正系数计算公式,可对箱梁涡振风洞试验结果进行修正,确保试验结果在实际工程中应用的可靠性。
结论可指导箱梁抗风试验结果的修正,为箱形主梁的抗风设计提供参考。
