爆炸荷载作用下钢筋混凝土构件缩尺效应的数值模拟研究

刘子超 吴俊，* 喻君 冯晓伟

爆炸荷载作用下钢筋混凝土构件缩尺效应的数值模拟研究

刘子超1吴俊1，*喻君2冯晓伟3

（1.上海工程技术大学城市轨道交通学院，上海 201620； 2.东南大学土木工程学院，南京 210008； 3.中国工程物理研究院总体工程研究所，绵阳 621999）

基于一组用于爆炸荷载下钢筋混凝土构件动力响应的无量纲相似准则，结合已有钢筋混凝土板缩尺抗爆试验数据，采用显式动力有限元软件LS-DYNA及弹塑性混凝土损伤本构模型，建立爆炸荷载作用下原型和缩尺钢筋混凝土板有限元模型，研究缩尺效应中缩尺系数、材料断裂能和材料应变率对钢筋混凝土板动力响应相似性的影响。结果表明：①采用弹塑性损伤本构模型能有效反映钢筋混凝土构件动力响应的缩尺效应，且缩尺模型的破坏形式及位移满足相似率；②当缩尺系数为0.2时，缩尺数值模型无法有效表征原型构件的损伤分布及位移响应，使其不满足钢筋混凝土板动力响应的相似率；③混凝土材料断裂能对构件动力响应的相似率影响不大，而混凝土应变率对缩尺模型的动力响应具有较大影响。研究结果可为钢筋混凝土构件抗爆试验中缩尺系数和模型材料选择、有限元模型中相关材料断裂能和应变率选取提供有效建议。

爆炸， 缩尺效应， 钢筋混凝土板， 混凝土损伤模型

0 引 言

近年来恐怖袭击、意外爆炸事故在世界范围内频繁发生。爆炸事故不仅对建筑结构造成巨大破坏，更使人身安全、财产受到重大损失。故结构抗爆性能是防护工程的主要研究方向之一。由于结构的原型抗爆试验受到人力、成本和时间等因素限制，采用缩尺模型是研究结构抗爆性能的有效方法。为获得缩尺模型和原型之间的相似性，必须要求关键物理现象在两个尺寸上相同，这可通过确定无量纲量来实现。因此，采用无量纲分析法是进行缩尺模型设计的重要准则之一［1］。

在20世纪60年代，国外学者进行了大量现场测试用于分析爆炸冲击波的缩尺效应。研究得出可采用立方根缩尺法则对爆炸荷载进行缩尺描述［2］。虽然立方根缩尺法则已广泛用于表征爆炸荷载缩尺效应，但钢筋混凝土（Reinforced Concrete，RC）结构在爆炸荷载作用下动力响应的可缩尺性尚不明确，尤其是如果假设混凝土的性能是由其强度和断裂能决定，那么在不同尺度上使用相同材料就违反了相似法则。鉴于此，国内外学者做了一系列现场缩尺模型试验研究工作。Zhang等［3］开展了缩尺系数0.8和0.6的RC梁野外爆炸试验，结果表明，虽然不同缩尺系数的RC梁破坏模式相似，但较大尺寸下RC梁的损伤更显著，且损伤程度和位移值并不满足相似关系。Forsén［4］进行了原型和缩尺系数0.25的RC板接触爆炸实验，探讨相似准则在接触爆炸分析中的适用性，研究表明，存在与缩尺系数无关的板开坑尺寸和炸药量之间的函数关系。Wachtell等［5］对缩尺系数0.3、0.2、0.125和0.1的4种RC挡墙结构进行了现场爆炸试验，研究得出当缩尺系数为0.3和0.1时，缩尺模型可较好预测原型结构的承载力。Wang等［6］对缩尺系数0.8和0.6的RC板进行了现场爆炸试验，研究RC板缩尺效应的影响，试验结果表明，原型与缩尺RC板具有相似的破坏模式，且缩尺RC板损伤程度小于原型，表明RC板存在缩尺硬化效应，但也发现随着缩尺系数减小，RC板的局部损伤范围变大，因此建议当采用缩尺RC板的损伤参数（位移、开坑尺寸等）预测原型结果时，应考虑材料应变率和断裂能的影响，对缩尺RC板的结果进行修正。

随着有限元技术的发展，使其可用于研究爆炸荷载作用下RC结构的动力响应及缩尺效应。荆松吉等［7］通过相似理论建立多层混凝土/土复合介质内爆炸的缩尺模型，并运用LS-DYNA对其原型和缩尺模型的毁伤效应进行了数值模拟，研究表明，缩尺模型与原型的毁伤参量具有较好的相似性；在选取合适缩尺系数的条件下，通过缩尺试验对原型试验的毁伤效应进行论证分析是可行的。Pang等［8］采用LS-DYNA对内部爆炸作用下深埋RC拱结构的缩尺效应进行了数值模拟研究，具体研究了重力、材料断裂能及应变率对原型及缩尺模型的影响。研究表明，对于深埋条件下的RC拱结构，其重力及钢筋应变率对缩尺模型的动力响应有较大影响，谢述春等［9］基于量纲分析法建立了多层混凝土介质内爆炸毁伤效应的模型，并对其毁伤效应参量和毁伤形态的相似性进行了数值模拟研究，结果表明，不同装药深度下的原型与缩尺模型的毁伤形态相同，毁伤效应参量符合相似规律；随着缩尺系数的减小，毁伤效应参量与原型的偏离程度增大，因此建议应选用缩尺系数大于0.25的模型试验结果预测原型的内爆炸毁伤效应。

综上，目前对于RC结构的抗爆分析，主要为现场试验和数值模拟。考虑到开展原型足尺试验的条件及成本有限，往往进行野外缩尺模型试验，继而通过有限元模型验证缩尺试验结果，使其可用于预测原型结构的抗爆动态响应。因此，对缩尺模型进行有限元数值模拟时，应该考虑模型缩尺效应的影响，从而使其用于原型结构动力响应的预测更加准确。然而，此方面的研究并不多，一方面缺乏缩尺效应项，如缩尺系数、材料断裂能和应变率对缩尺模型动态响应相似率的影响分析；另一方面，在进行有限元方法分析缩尺效应时，其材料本构模型及相关参数的确定未有深入探讨。因此，本文首先以爆炸荷载立方根缩尺准则和RC结构无量纲相似理论（Π项）为基础，利用有限元软件LS-DYNA［10］，采用弹塑性损伤本构模型表征混凝土，建立原型及不同缩尺系数下RC板的有限元模型，通过与已有试验中RC板的损伤形式及位移值比较，探讨并验证原型及缩尺有限元模型的合理性。进一步采用验证的缩尺有限元模型研究相似系数0.8～0.2条件下，RC板抗爆动力响应的相似关系，论证采用有限元模型进行缩尺模型研究的可行性。最后，讨论了违反缩尺法则项（材料断裂能和应变率）对原型和缩尺RC板动力响应相似率的影响，从而为指导爆炸荷载作用下缩尺RC结构的相关试验设计和数值模型建立提供理论依据。

1 缩尺准则

1.1　爆炸荷载缩尺

式中，表示常数。

假设空气中由球形炸药引起爆炸冲击波所涉及的变量有爆炸物半径、超压峰值、冲量和持续时间。在某处响应涉及的变量有爆距、炸药质量（通常采用等效TNT质量）、空气的密度0和声速0，基于3个国际制基本量纲（即SI制长度、时间和质量），可由Π定理得出爆炸荷载的无量纲量表达式［12］：

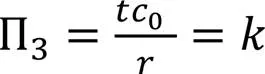
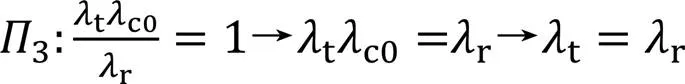
炸药量的缩尺系数可通过4获得：

最后冲量缩尺系数可通过5获得：

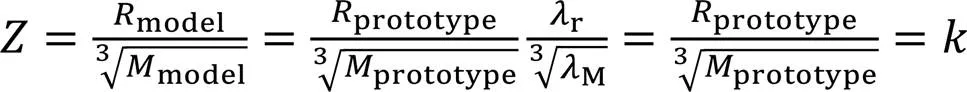
可见比例距离虽不是无量纲项，但立方根缩尺法则对爆炸波缩尺效应的描述与Π定理保持一致［11］。

1.2　RC构件缩尺

由上述Π项可知，RC模型构件的尺寸可由Π6，Π7和Π8项确定，其中Π6项为几何缩尺因子，与爆炸波缩尺效应中Π1项一致；如果在缩尺构件中采用的混凝土与原型的材料相同，则混凝土密度保持不变，结构质量（Π7）缩尺系数为3；对于钢筋，由Π8项可知只要保持钢筋横截面积与两个长度量的乘积之间的比例恒定（保持配筋率恒定）即满足要求。另外，在原型和模型中使用相同的材料，可使其抗压强度和失效应变满足相似率（Π9和Π11项），但缩尺模型中材料断裂能过大（Π10项）。因此在静载试验中，违反材料特性的断裂能缩尺项（Π10）通常用于解释RC构件的力学响应不成比例，即尺寸效应［14-15］。此外，Π12项表明在缩尺模型中，材料具有更高的应变率（为缩尺系数的倒数），从而导致缩尺模型中材料强度的提高。这两种违反相似性的现象（Π10和Π12项）将会导致通过缩尺模型结果预测原型结果与实际的原型结果有一定误差。由于实验室或现场缩尺模型试验中，无法定性分析上述2项对理论结果的影响，因此本文将采用数值计算方法对模型中无法缩尺项进行探讨。

2 RC板数值计算模型

2.1　有限元模型

采用LS-DYNA有限元软件对RC板进行建模及计算分析。Wang等［6］对RC板抗爆缩尺效应进行了野外爆炸试验，图1为试验现场布置图，其中RC板两端为槽钢固定，炸药放置于板中心上方。试验中RC板原型尺寸为1 250 mm×1 250 mm×50 mm，缩尺系数0.8和0.6的RC板尺寸分别为1 000 mm×1 000 mm×40 mm和750 mm×750 mm×30 mm。板中双向布置直径为6 mm的HRB335级钢筋，间距75 mm。考虑对称性，建立1/4有限元模型，其中原型RC板长和宽均为625 mm，板厚为50 mm。钢板长度为625 mm，截面尺寸厚度为20 mm，宽度为200 mm。基于网格收敛性分析，原型RC板的网格尺寸为3 mm，有限元模型及钢筋布置如图2所示。

图1　RC板试验布置图［6］

图2　RC板有限元模型（1/4模型）

2.2　材料本构模型及参数

在近年的研究中，学者们提出了许多混凝土材料模型［16-19］用于表述材料在强动载作用下的动态性能。LS-DYNA中KCC模型［16，20］能较好地模拟混凝土材料在动荷载作用下的应变硬化、应变软化及应变率效应。因此，本文拟采用KCC材料模型模拟混凝土材料，该模型有3个独立强度面：峰值强度面、屈服面以及残余强度面［16］。

对于普通混凝土材料参数可采用KCC模型自动生成参数［21-24］。本文中普通混凝土主要力学性能参数见表1，将其输入到材料模型中，即可得普通混凝土的强度面等参数，如表2所示，其中压缩和拉伸损伤因子1和2用于描述材料在压、拉峰值后的断裂能的变化，可根据相关计算方法得出［20-21］。材料应变率效应通过在模型中输入强度增长曲线（Dynamic Increase Factor，DIF）的方法表征，本文采用的混凝土DIF曲线如图3所示。

表1　 试验中混凝土强度

表2　 KCC中38 MPa混凝土强度面参数

图3　普通混凝土DIF曲线

数值模型中板的纵向受力钢筋选用HRB335级钢筋，采用塑性随动（Plastic-Kinematic）模型模拟，屈服强度484 MPa。支座处槽钢为刚体，与混凝土板端部设置自动面对面接触（AUTOMATIC _SURFACE_TO_SURFACE），其静、动摩擦系数分别取为0.3和0.2。对于原型RC板，按现场试验考虑比例距离为0.518 m/kg1/3和0.591 m/kg1/3的2种工况，爆炸波通过关键字LOAD_BLAST_ENHANCED的方式施加于RC板的表面。

3 计算模型验证

3.1　原型RC板模型

原型RC板在不同比例距离下的损伤形式如图4（a）和图4（b）所示。图4（a）为比例距离0.591 m/kg1/3下RC板破坏模式，由图可知RC板主要呈现弯曲破坏，迎爆面产生一条居于中心的主裂缝，而背爆面有一定程度的剥离破坏产生，同时一些斜剪裂缝沿中心向外扩散。由图4（b）可知，当比例距离为0.518 m/kg1/3时，RC板在现场试验中呈现弯曲和背部剥离破坏，需注意的是由于数值模型未采用侵蚀算法（Erosion），因此没有显示出RC板迎爆面开坑状态。但从裂缝发展趋势与损伤范围来看，该数值模型仍可较好地反映现场实测的情况，验证了原型RC板数值模型的有效性。

图4　现场爆炸试验中原型RC板破坏形式

表3给出了现场试验和数值模型中原型RC板在不同比例距离下跨中最大位移值。可看出数值模拟结果与试验结果的误差均在10%以内，表明本文建立的原型RC板数值计算模型的正确性。之后，将对上述原型RC板数值模型进行缩尺，进一步验证缩尺RC板数值模型的有效性。

表3　 不同比例距离下原型RC板跨中最大位移对比

3.2　缩尺RC板模型

Wang等［6］对RC板进行了缩尺系数0.8和0.6的现场爆炸试验，比例距离分别为0.591 m/kg1/3和0.518 m/kg1/3。需要说明的是，在现场爆炸试验中，缩尺RC板的长、宽和厚度严格按照比例缩尺，而钢筋尺寸和间距没有进行缩尺，所有工况均使用直径为6 mm的钢筋，并且其间距固定为75 mm。因此对于缩尺RC板数值模型，首先将钢筋尺寸和间距与试验工况保持一致。对原型RC板数值模型中3 mm网格尺寸进行缩尺，当缩尺系数为0.8和0.6时，其有限元网格尺寸分别为2.4 mm和1.8 mm，从而保证所有模型中网格数量相同。调整炸药质量及高度，使之满足缩尺准则。模型计算结果如图5和图6所示。

由图5和图6可知，在2种比例距离下，RC板表现为弯曲破坏，其中正面有一条主裂缝，背面由中间向四周扩散形成细裂缝。随着缩尺系数减小，试验与数值模型结果均表明构件中部损伤分布范围有一定的减少，表明数值模型的准确性。表4给出了不同缩尺条件下RC板跨中最大位移，当比例距离为0.591 m/kg1/3时，缩尺系数0.6的RC板数值模型结果与试验结果有一些误差，这可能是由于在现场试验中对于缩尺系数0.6的试件，实际采用130 g而不是按照比例缩尺的138 g的炸药当量（数值模型采用138 g炸药当量），因此使数值计算结果大于试验结果。

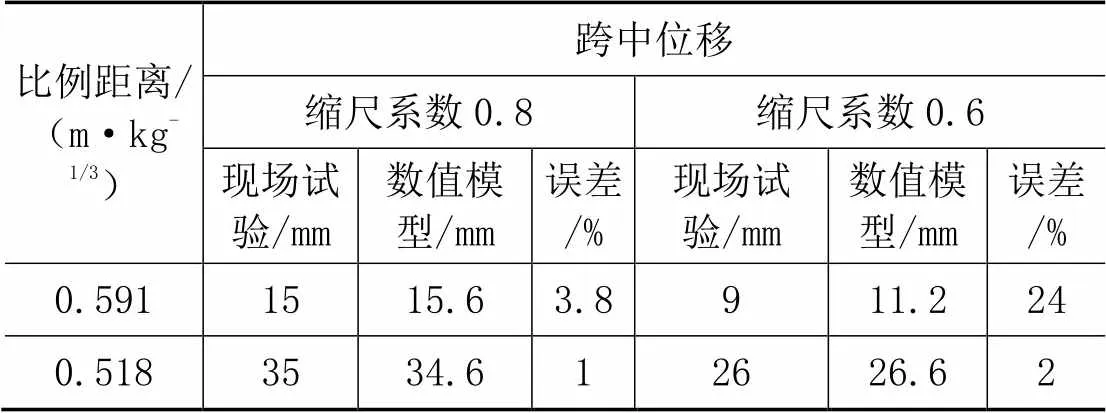
表4　 缩尺系数0.8和0.6条件下现场试验及数值模拟RC板最大挠度对比

需要注意的是现场试验中缩尺RC板的钢筋尺寸和间距与原型RC板一致，并没有严格遵循缩尺准则，从而使现场缩尺RC板的配筋率要高于原型。因此，进一步对上述2种比例距离的缩尺数值模型进行修正，即把缩尺数值模型中的配筋率进行缩尺，得到修正后的缩尺计算模型，其最大位移如图7所示。图中“缩尺曲线”为参考线，代表RC板在理论缩尺系数下的位移值（即根据原型数值计算结果分别乘以缩尺系数得到的相应位移值），同时在每个缩尺系数对应的理论位移值处标出了±10%误差区间；“修正数值模型”代表对RC板的配筋率进行缩尺后的计算模型。可以看出，2种比例距离条件下，修正数值模型计算结果与理论值接近，并且大于试验值，说明试验中未按配筋率缩尺将导致RC板硬化。对于比例距离0.591 m/kg1/3，修正数值模型的计算结果与缩尺曲线具有较好的吻合度，而现场试验由于未考虑配筋率的缩尺，与理论曲线有较大的误差，特别是随着缩尺系数减小，钢筋配筋率对计算结果有较大影响。当比例距离为0.518 m/kg1/3时，修正数值模型与理论值也吻合较好，说明修正缩尺RC板数值模型的准确性。但也可看出，现场试验虽未对构件配筋率进行缩尺，其试验结果与理论值亦在10%的误差范围内。这可能是随着比例距离减小，RC板从整体破坏过渡到局部损伤破坏。而对于局部损伤破坏，钢筋对RC构件的抗爆承载力贡献不大［25］。

图7　缩尺系数0.6和0.8条件下RC板跨中最大位移图

4 RC板缩尺效应影响因素

4.1　缩尺系数

基于第3节中验证的原型和缩尺RC板数值模型，分别采用缩尺系数0.8、0.6、0.4和0.2对原型RC板进行缩尺，研究缩尺系数对RC板动力响应的影响。考虑比例距离=0.591 m/kg1/3和=0.518 m/kg1/3共2种工况，其中板的几何尺寸、配筋率和爆炸荷载均考虑缩尺，以满足第2节中相似准则。但对断裂能和应变率项（Π10和Π12项），由于假设缩尺及原型模型中均采用相同材料，因此数值模型中这2项不缩尺，稍后章节将会重点讨论这2项对理论结果的影响。对应上述缩尺系数的缩尺模型网格尺寸分别为2.4 mm、1.8 mm、1.2 mm和0.6 mm，使不同缩尺模型中网格数相同。

表5总结了不同缩尺模型在同一比例距离下的损伤破坏形式。可以看出，不同缩尺系数下RC板跨中均有一条主裂缝，呈现弯曲破坏，表明破坏形式具有相似性，迎爆面中心损伤范围随着缩尺系数减小亦有一定减少，表明RC板具有缩尺硬化效应。对于背爆面，裂缝从中心部向外径扩展，形成一系列细小裂纹，损伤分布较一致。但需注意的是随着缩尺系数减小，两个比例距离下RC板迎爆面的损伤范围有向外扩展的趋势，主要原因可能是在爆炸荷载作用下RC构件损伤效应存在压碎和剥离破坏等面效应［7］，用于面效应的能量在总能量中所占的比例随缩尺模型的变小而增大，即缩尺模型越小，面效应越强，对几何相似律的破坏越严重。因此，从数值模型计算结果来看，随着缩尺系数减小，RC板中心主裂缝周围的细裂缝逐渐增多，损伤范围逐步扩展，从而导致缩尺系数为0.2时，其中心裂缝外的损伤程度与原型有较大不同。

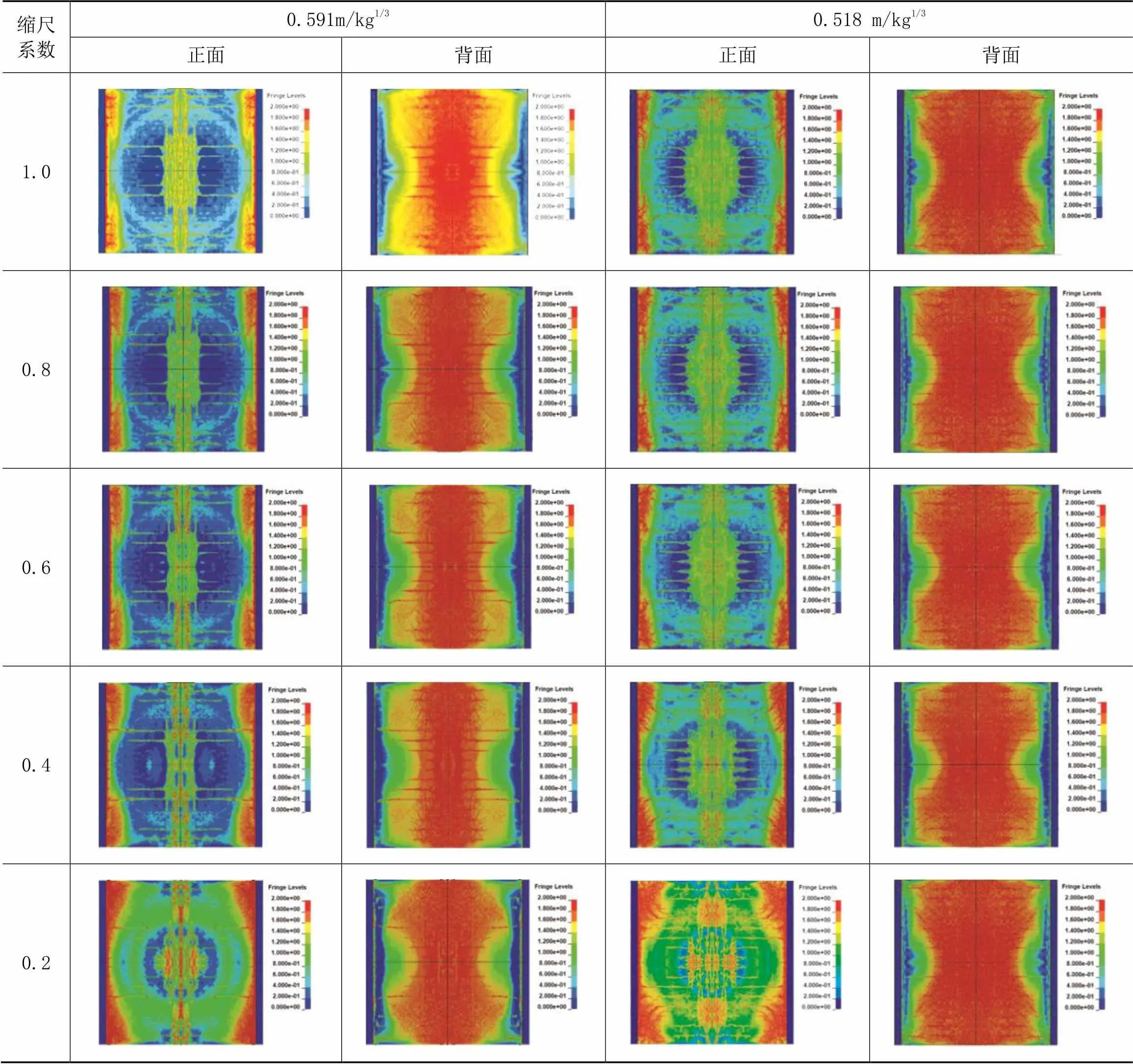
表5　 不同比例距离下缩尺模型结果对比

图8给出了2种比例距离下，不同缩尺模型的最大位移。可以看出缩尺数值模型（除缩尺系数0.2外）的跨中最大位移满足相似关系，与理论值均在10%误差范围内。当缩尺系数为0.2时，数值模型计算结果与理论值之间的误差大于10%。结合上述损伤分布结果可表明对于缩尺数值模型，当缩尺系数为0.2时，其损伤分布和位移均不能有效反映原型RC板的动力响应，使其不具有相似性。

4.2　混凝土材料断裂能

缩尺试验中采用与原型相同的材料，故混凝土材料断裂能项（Π10）无法满足缩尺准则。因此本节拟采用数值计算的方法，研究材料断裂能对RC板缩尺效应的影响，并主要考虑混凝土材料压缩断裂能（c）和拉伸断裂能（f）。KCC模型中可通过调整参数1和2分别描述材料在压缩和拉伸条件下断裂能变化。原型中混凝土材料压缩和拉伸断裂能分别为13.83 MPa·mm和0.15 MPa·mm。基于Π10项，不同缩尺条件下的压缩和拉伸断裂能取值如表6示。

图8　不同缩尺系数下RC板跨中最大位移趋势图

表6　 缩尺模型中断裂能及b1和b2取值

图9显示了断裂能缩尺后的数值模型计算结果，其中“缩尺曲线”为严格按照缩尺理论下的位移值，与3.2节定义一致；“修正数值模型”为3.2节验证过的缩尺RC板的数值模型，即RC板的尺寸、配筋率和爆炸波均严格按照缩尺理论，但材料断裂能和应变率不缩尺；“断裂能缩尺”为数值模型中，仅应变率项不缩尺，其余参数均按照缩尺准则缩尺。由图9可知，在2种工况下，断裂能缩尺对理论结果影响不大（误差<10%），表明当进行缩尺RC板数值模拟时，混凝土材料断裂能项（Π10）虽然违反缩尺准则，但其结果与原型RC板的位移值满足相似率。另一方面，对于现场缩尺试验，如采用与原型相似的材料，即保持材料抗压强度和失效应变一致，缩尺模型结果仍可满足相似率。但必须注意的是当缩尺系数为0.2时，即使数值模型中考虑材料断裂能缩尺，其计算结果与理论值的误差仍大于10%，表明该条件下的缩尺模型无法有效反映原型构件的动态响应。

4.3　混凝土材料应变率

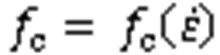
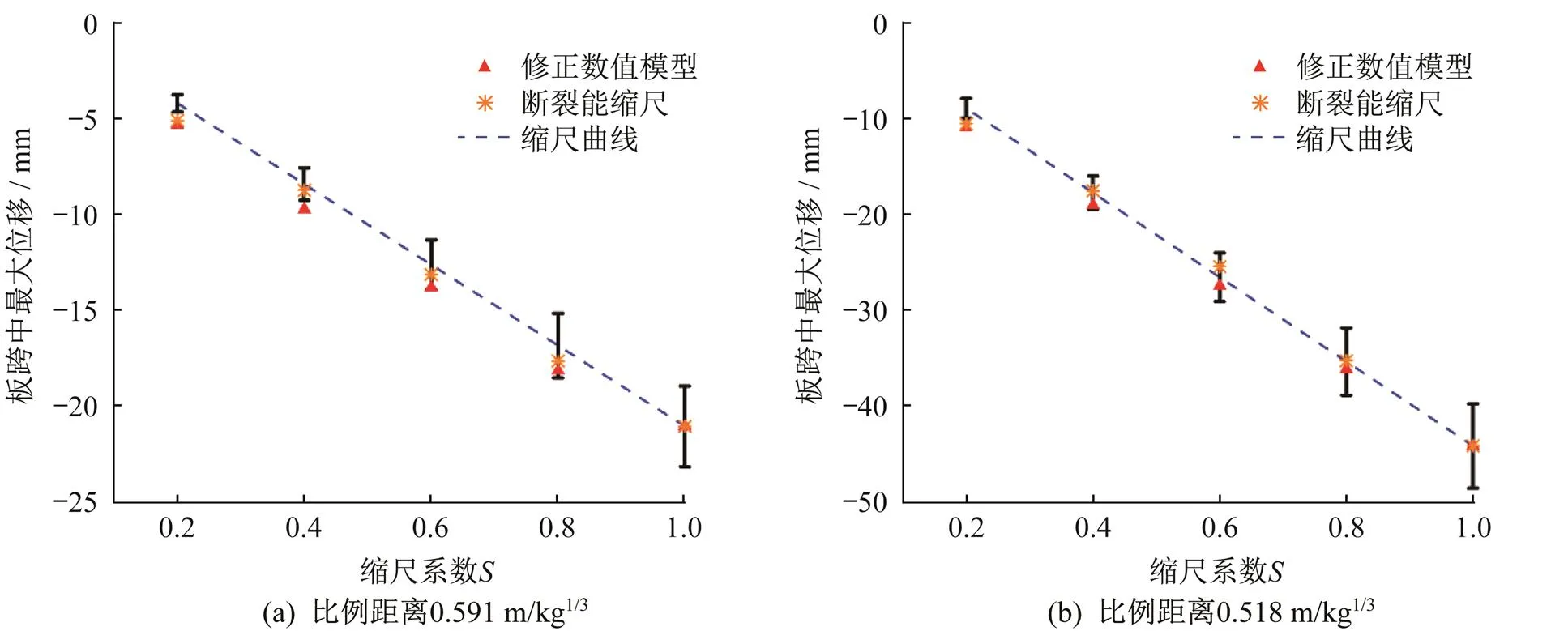
图9　不同比例距离下断裂能缩尺结果曲线图

图10　不同缩尺模型中应变率均值（比例距离0.591 m/kg1/3）

图11　数值模型中输入的混凝土抗压与抗拉DIF曲线

图12给出了RC板跨中最大位移图。由图可知，当DIF不缩尺，其计算结果与理论值较接近，位移值满足相似率；当缩尺模型中DIF=1和动态增长系数为DIF×缩尺系数时，数值计算结果与理论值具有一定的误差。对于DIF=1，由于不考虑材料应变率，缩尺RC板最大位移值远大于理论值，表明在进行原型和缩尺RC构件数值模拟时，应考虑混凝土材料的应变率。当缩尺模型中动态增长系数为DIF×缩尺系数时，其计算结果与理论值有一定偏离，且随着缩尺系数越小偏差越大，表明DIF随缩尺减小将会造成RC构件软化。特别是当缩尺系数为0.2时，RC板跨中最大位移与DIF=1工况结果接近，这主要是由于在缩尺0.2时输入的DIF拉伸曲线与DIF=1的模型相似，也可看出材料动态拉伸强度对爆炸荷载下RC板位移有较大影响。

以上结果表明，在数值模型中如果考虑缩尺后混凝土材料强度系数减小（即输入曲线为DIF×缩尺系数），将导致缩尺条件下应变率效应减弱，使计算结果与实际不符，且不满足相似率。因此对于缩尺数值模型，仅输入与原型材料一致的DIF，其计算结果可满足RC构件动态响应相似率，但相似系数为0.2时，缩尺模型无法有效反映原型构件的动态响应。

图12　三种DIF工况下RC板跨中最大位移曲线图

5 结 论

本文基于一组用于缩放爆炸荷载下RC结构的无量纲项（Π项），结合已有RC板缩尺抗爆试验数据，采用动力有限元软件LS-DYNA及弹塑性混凝土损伤本构模型，对原型和缩尺模型抗爆性能的缩尺效应进行数值模拟分析，讨论了数值模型中缩尺系数、材料断裂能和材料应变率对构件动态响应相似率的影响，得出以下结论：

（1） 采用弹塑性损伤本构模型的有限元模型能有效反映现场爆炸试验中缩尺模型的强化效应。

（2） 在满足缩尺准则的条件下，缩尺系数0.4～0.8的缩尺有限元模型能够较准确地反映原型RC板的动态响应（破坏形式、损伤分布和位移值）且满足相似率，而当缩尺系数为0.2时，缩尺有限元模型无法有效预测原型构件的动态响应。

（3） 有限元模型中，材料断裂能对模型的动态响应相似率影响不大，表明虽然混凝土断裂能无法满足缩尺准则，现场缩尺模型试验仍可有效地反映原型构件的抗爆动态响应。

（4） 有限元模型中，混凝土材料应变率对构件动态响应的相似率有较大影响，因此建议当采用缩尺有限元模型分析预测原型结构动态响应时，可采用与原型材料相同的动态强度提高系数函数。

缩尺试验是研究RC结构抗爆响应的有效方法，而采用数值模型可研究在现场试验中违反相似准则因素的影响。由此，可通过基于建立在满足缩尺法则的有限元模型对预期结果进一步分析。

［1］ Bridgman P W.Dimensional analysis［M］.Yale University Press，1922.

［2］ Kingery C N.Air blast parameters versus distance for hemispherical TNT surface burst［R］.Ballistic Research Laboratories，Report No.1344.Aberdeen，Maryland，1966.

［3］ Zhang D，Yao S J，Lu F Y，et al.Experimental study on the scaling of RC beams under close-in blast loading［J］.Engineering Failure Analysis，2013（33）：497-504.

［4］ ForséN R.Experiments used for comparison of blast damage to full scale and one fourth scale reinforced concrete structures［R］.Minutes of the 24th Explosive Safety Seminar 2，St.Louis，Missouri，1990.

［5］ Wachtell S.Comparison of blast response-scaled vs.full-size concrete structures［J］.Annals of the New York Academy of Science，1968，152（1）：829-850.

［6］ WANG W，ZHANG D，LU F Y，et al.Experimental study on scaling the explosion resistance of a one-way square reinforced concrete slab under a close-in blast loading［J］.International Journal of Impact Engineering，2012（49）：158-164.

［7］荆松吉，卢芳云，张震宇，等.混凝土复合介质内爆炸毁伤效应的模化方法研究［J］.弹箭与制导学报，2008，28（2）：93-96.

Jing Songji，Lu Fangyun，Zhang Zhenyu，et al.Research on modeling method of damage effect of explosion in concrete composite medium［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2008，28（2）：93-96.（in Chinese）

［8］ PANG S，ABRAHAM C，YANG Y，LIEW J.Scaling of buried composite arch structure under internal blast loading［C］//5thInternational conference on Protective Structures，Ponan，Poland，Aug.19-23，2018，486-493.

［9］谢述春，姜春兰，王在成，等.多层混凝土介质内爆炸相似性分析［J］.兵工学报，2019，06-1198-09.DOI：10.3969/j.issn.1000-1093.2019.06.010

Xie Shuchun，Jiang Chunlan，Wang Zaicheng，et al.Analysis of similarity law of explosion in multi-layer concrete medium［J］.Acta Armamentarii，2019，06-1198-09.（in Chinese）

［10］ Hallquist J.LS-DYNA keyword user's manual［M］.Livermore Software Technology Corporation （LSTC），2007.

［11］ Baker W E，Westine P S，Dodge F T.Similarity methods in engineering dynamics［J］.Hayden Book Company，1973：383-385.

［12］ Coutinho C P，Baptista A J，Rodrigues J D.Reduced scale models based on similitude theory：a review up to 2015［J］.Engineering Structures，2016（119）：81-94.

［13］ Benjamin S，Christoph R，Werner R.Scaling rules for the analysis of blast loaded concrete structures-a critical literature review［C］//6th International Conference on Design and Analysis of Protective Structures，Nov.29-Dec.01，2017，Melbourne，Australia，504-513.

［14］ BažAnt Z P.Size effect in blunt fracture： concrete rock，metal［J］.Journal of Engineering Mechanics，1984.110：518-535.

［15］ Carpinteri A.Fractal nature of material microstructure and size effects on apparent mechanical properties［J］.Mechanics of Materials，1994（18）：89-101.

［16］ Malvar L J，Crawford J E，Wesevich J W，et al.A plasticity concrete material model for dyna3d［J］.International Journal of Impact Engineering，1997，19 （9-10）：847-873.

［17］ Polanco L M，Hopperstad O S，Berstad T，et al.Numerical predictions of ballistic limit for concrete slabs using a modified version of the HJC concrete model［J］.International Journal of Impact Engineering，2008（35）：290-303.

［18］ Riedel W，Kawai N，Kondo K.Numerical assessment for impact strength measurements in concrete materials［J］.International Journal of Impact Engineering，2009 （36）：283-293.

［19］ Holmquis T J，Johnson G R，Cook W H.A computational constitutive model for concrete subjected to large strains，high strain rates，and high pressures［C］//JACKSON N，DICKERT S.The 14th International Symposium on Ballistics.Quebec： American Defense Preparedness Association，1993：591-600.

［20］ Wu J，Chew S H.Field performance and numerical modelling of multi-layer pavement system subject to blast load［J］.Construction and Building Materials，2014（52）：177-188.

［21］吴俊，李亮，杜修力.爆炸荷载作用下新型多层道面体系动力响应的三维数值模拟［J］.北京工业大学学报，2016，42（9）：1355-1362.

Wu Jun，Li Liang，Du Xiuli.Three-dimensional numerical simulation on the dynamic response of a multi-layer pavement system subject to blast loading［J］.Journal of Beijing University of Technology，2016，42（9）：1355-1362.（in Chinese）

［22］吴俊，李亮，杜修力，复合道面结构抗冲击性能试验与数值模拟［J］.建筑科学与工程学报，2018，35（2）：71-78.

Wu Jun，Li Liang，Du Xiuli.Experiment and numerical simulation on impact resistance of composite pavement slab［J］.Journal of Architecture and Civil Engineering，2018，35（2）：71-78.（in Chinese）

［23］ Yu J，Gan Y，Wu J，Wu H.Effect of concrete masonry infill walls on progressive collapse performance of reinforced concrete infilled frames［J］.Engineering Structures，2019（191）179-193.

［24］ Hu G，Wu J，Li L.Advanced concrete model in hydrocode to simulate concrete structures under blast loading［J］.Advances in Civil Engineering，2016，1-13.

［25］ Clifton J R.Penetration resistance of concrete-a review［S］.Special Publication，National Bureau of Standards，Washington D C，1982：480-485.

Numerical Study on the Scaling Effect of Reinforced Concrete Members under Blast Load

LIUZichao1WUJun1，*YUJun2FENGXiaowei3

（1.School of Urban Railway Transportation，Shanghai University of Engineering Science， Shanghai 201620， China； 2.School of Civil Engineering， Southeast University， Nanjing 210008， China； 3.Institute of Systems Engineering，China Academy of Engineering Physics， Mianyang 621999， China）

Based on a set of dimensionless terms and the existing test data of the reinforcement concrete slab under blast load，the LS-DYNA and the damaged elastic-plastic concrete constitutive model were adopted to establish the finite element model of prototype and scaled reinforced concrete slabs under blast load. The influence of scale effects on the blast resistance of reinforced concrete slabs and its corresponding was studied. The factor of scale factor，material fracture energy and material strain rate in the numerical model on the similarity of damage pattern and damage parameters of prototype and scaled reinforcement concrete slabs were discussed. The results show that： ① The numerical model could effectively reflect the scale strengthening effect of reinforced concrete components，and the similarity of damage pattern and damage parameters of prototype and scaled reinforced concrete slabs can be achieved； ② When the scale factor was less than 0.2， the scaled numerical model cannot effectively characterize the damaged situation and displacement response of the prototype component； ③ The scale of the fracture energy of concrete materials had little effect on the dynamic response of the prototype member， whereas the concrete strain rate had a greater influence on the results of the scaled model. The research results can provide effective suggestions for determining scale factor of the reinforced concrete components in field blast test，and the relevant parameters of fracture energy and strain rate in the finite element model.

explosion， scale effect， reinforced concrete slab， concrete damaged model

2021-03-01

国家自然科学基金（51978246，52078288）

刘子超，男，研究方向为混凝土结构抗爆。E-mail：liuzichao0507@163.com

联系作者：吴 俊（1980-），男，博士后，教授，研究方向为混凝土结构抗爆抗冲击。E-mail： cvewujun@163.com