机器人在轨装配无标定视觉伺服对准方法

2021-07-07贾庆轩段嘉琪陈钢

航空学报 2021年6期

贾庆轩，段嘉琪，陈钢

北京邮电大学自动化学院，北京 100876

随着对太空开发的不断深入，空间结构的大型化是未来航天事业发展的主要趋势。许多科学研究计划都要求有大型的空间结构作为基础，如空间站需要千米级尺寸的太阳能电池阵列来提供充裕的能量[1]；高分辨率对地观测需要百米级的星载天线来提高精度[2-3]；深空探测飞行器需要用超轻薄膜构成的巨型太阳帆来利用太阳光子作为动力[4-5]。但是受运载火箭整流罩尺寸的限制，这类大型空间结构无法由运载器直接送入太空，需要由桁架在轨装配而成[6-10]。

桁架在轨装配过程中，空间机器人不可避免地需要利用视觉伺服完成大量对准工作。传统的机器人视觉伺服系统都是在对相机模型和机器人模型标定的基础上实现的，但在轨装配过程中无法实现对系统的精确有效标定，譬如美国用于在轨装配的Sky-worker机器人[11]有一只手臂专门搭载相机。每次进行装配对准时，该机械臂就会规划运动到相关位置完成“看”的动作。因此每次对准操作手眼之间的关系都不确定，而重新标定十分复杂难以实现且会导致装配效率低下，继续沿用原标定结果则会产生很大误差[12]。除此之外已标定结果也会受空间恶劣环境的影响而发生退化进而影响装配精度，如相机标定参数会受到高辐射的影响而退化。无标定视觉伺服可在不预先对相机模型、机器人模型和手眼关系标定的前提下，直接利用图像上的系统误差，设计控制器驱动机器人运动，使系统收敛到一个容许的误差域内[13]。无标定视觉伺服省去了繁琐的标定过程，在控制效率、应用便利性及性能上均有较大的优势[14]。

此外，一方面考虑到机器人每次进行桁架对准操作时，所持桁架随着装配进行其形状质量都会发生变化，可能是尚未装配连接的简单桁架，也可能是已部分搭建完成的大型桁架。因此在轨装配视觉伺服系统控制对象的惯性参数不确定性。另一方面用于在轨装配的机器人通常为带有机械臂的独立航天器。虽然这类航天器可以在进入太空前完成系统参数的标定，但随着在轨装配的进行，航天器燃料会逐渐消耗、目标桁架会被释放，机器人系统的惯性参数会发生变化[15]。传统的基于机器人与被操作对象模型的控制方法未将其考虑在内，导致对准精度不高甚至是对准失败的问题。滑模控制凭借其快速响应、对参数变化及扰动不灵敏、无需系统在线辨识及物理实现简单等优点被广泛应用于参数未定的机器人控制领域[16]。对于在轨装配的无标定视觉伺服系统而言，最为直接的思路就是将滑模控制方法扩展到无标定视觉伺服控制中。但图像特征点的深度信息以倒数形式非线性的呈现在图像雅可比矩阵中，无法满足滑模控制中对未知参数线性化表述的要求。

国内外学者针对参数不定的无标定视觉伺服展开了研究：Cheah等[17]研究了当特征点的深度信息保持不变时，用于描述机器人关节空间与图像空间的系统模型可以使用未知参数进行线性化描述，这为自适应控制用于无标定动力学视觉伺服提供了有力的理论支撑；在此基础上，Cheah等[18]最早对无标定视觉伺服进行了研究，在目标深度信息缓慢变化时实现无标定视觉伺服，但该方法雅可比矩阵自适应估计通常需要假设深度信息为固定值或者是缓变值，以便于未知变量的线性参数化与自适应律对这些变量进行在线估计。Santamaria等[19]将相机焦距与深度信息的比值作为参数，并利用PnP(Perspective-n-Point)算法，对该比值进行在线估计，在相机光轴位置与垂直度弱假设的条件下，该方法可以对雅可比进行较好的近似，在无人机的垂直起降控制中体现出良好的性能。Cheah等[20]对具有运动学和动力学不确定性的机器人设计了基于自适应算法的混合力位控制器，实现对未定参数的在线估计，保证了机器人雅可比矩阵在一定范围内变化时系统仍然是稳定的，但该方法需要经过复杂的参数估计，耗时长，无法满足大型空间结构的快速装配。Liu等[21]提出了深度雅可比矩阵，该深度雅可比矩阵单独提取与深度信息相关的项作为一个比例项，矩阵中不包含深度信息，使得未知参数线性的出现在机器人闭环动力学系统中；Liang等[22]在此基础上引入了自适应控制方法，由于无法获取深度参数的精确值，只能利用估计值进行代替，但是此方法无法从理论上保证系统的渐进性和稳定性。

综上所述，提出的机器人在轨装配无标定视觉伺服对准方法，在传统的无标定视觉伺服基础上，设计了深度估计器，满足了滑模控制对未知参数线性化要求，从而引入滑模控制方法实现对机器人运动状态的控制，解决了机器人及负载惯性参数不定导致对准精度低的问题，使系统能够在复杂的太空环境下完成在轨装配任务。

1 伺服系统原理

图像雅可比矩阵描述机器人关节运动与图像特征变化关系，是研究无标定视觉伺服对准系统的基础。而图像雅可比矩阵存在高度非线性，从简化的角度可以将其视为一系列局部范围内非线性关系的线性近似。图像雅可比矩阵的在线辨识的准确性将直接影响到控制系统性能的好坏。因此，本节将简单介绍图像雅可比矩阵的推导并选用卡尔曼滤波法完成在线辨识。

1.1 图像雅可比矩阵推导

采用针孔相机模型来描述所研究相机。假设空间中任意一点P在相机坐标系Tc中的坐标为(x,y,z)，即P=[xyz]T。点P在图像平面的投影在图像坐标系Ti下表示为Pi，即Pi=[uv0]T，则有

(1)

式中：λ为相机的焦距。定义相机相对于世界坐标系Tg的线速度和角速度分别为v=[vxvyvz]T和ω=[ωxωyωz]T，则空间点P相对于相机坐标系Tc的相对速度为

(2)

联立式(1)和式(2)可得

(3)

式(3)反映了单个特征点图像空间到操作空间的映射关系，设

Jfi=

(4)

式中：Jfi为单个特征点的图像雅可比矩阵，其值与相机的有效焦点长度λ以及目标深度信息z有关。则式(3)可以写为

(5)

式中：fi是某一特征点的2维图像特征矢量；r为相机在任务空间中的坐标参数。

若扩展到m个特征点可得

(6)

式中：Jf为狭义图像雅可比矩阵，f1,f2,…,fm代表m个特征点的2维图像特征矢量。

建立机器人运动学方程，即

(7)

联立式(6)和式(7)可得描述关节运动与图像特征变化关系为

(8)

式中：J为图像雅可比矩阵；n为机器人自由度数。

1.2 图像雅可比矩阵在线辨识

无标定视觉伺服系统的好坏很大程度上取决于图像雅可比矩阵在线辨识的准确度。因为在整个任务空间中，图像雅可比矩阵的变化是相当明显的，如果不能实现在线辨识，将无法保证图像反馈控制器的性能，甚至使系统出现振荡。卡尔曼滤波方法是一种误差方差最小的状态估计方法，普遍应用于实时状态估计、系统参数辨识和目标跟踪领域。相比于其他方法，卡尔曼滤波对图像雅可比的在线辨识具有更高的鲁棒性和抗干扰能力，是目前常用的方法之一。

将式(6)离散化可得

f(k+1)≈f(k)+J(r(k))Δr(k)

(9)

式中：k为连续过程的离散点；Δr(k)为相邻两个离散时间点之间相机坐标参数变化。

定义mn×1维观测矢量

(10)

定义图像雅可比矩阵的观测矢量x(k)为系统状态，机器人运动引起的图像特征变化为系统输出，即y(k)=f(k+1)-f(k)。建立系统状态方程

(11)

式中：C(k)状态变量到观测矢量的转换矩阵；η(k)、v(k)分别为状态噪声和图像观察噪声。

由此可建立基于卡尔曼滤波方法的图像雅可比矩阵的在线辨识递推方程

(12)

2 深度估计器设计

空间在轨装配过程中，伺服对准操作一般发生在粗对准之后，此时目标桁架与对应的接口距离较近，接口特征所在平面与相机成像平面基本平行，但是接口特征的深度信息未知。传统的深度信息估计方法有单目深度估计法和双目深度估计法。其中，单目深度估计法算法复杂、耗时长、实时性差、易受环境影响、估计精度难以保证。而双目深度估计法两个相机的位置距离限制了深度数据的获取，且机器人运动引起的抖动等不稳定因素使得两个相机的对齐困难。因此本小节在图像雅克比矩阵的基础上，利用最小二乘法设计深度估计器，通过对机器人和图像运动的测量数据来在线估计目标特征的深度值。所设计的深度估计器简单易行，只与特征提取精度相关，不受安装位置与机器人运动的影响，且估计精度可以满足对准需求。

根据式(4)建立的单个特征点图像空间到操作空间的映射关系，可得图像雅可比矩阵的前三列与目标特征点的深度值有关，重新整理可得

(13)

式中：Jt为相机平移运动对图像特征矢量的影响；Jw为相机旋转运动对图像特征矢量的影响。

将式(13)重新整理为

(14)

式(14)的右侧是观察到的光流减去由于相机旋转产生的光流。相减得到的剩余光流即为相机平移所导致的光流。将式(14)整理为紧凑的线性方程

Aθ=b

(15)

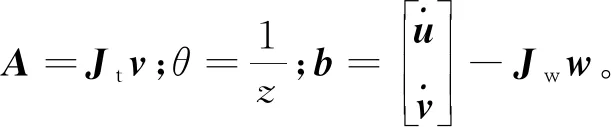
利用最小二乘法对上式中的目标特征深度值求解得

(16)

基于式(16)利用对图像雅可比矩阵的在线辨识结果可以实现对图像特征点深度信息的估计。在已知深度信息的基础上，则可以为引入滑模控制方法实现对动力学参数和负载参数未定情况下机器人关节的自适应控制提供基础。

3 视觉伺服滑模控制

基于前面两小节所研究内容，根据特征点的期望特征矢量即可得到机器人运动的期望关节角。从控制的角度来看，纯运动学的控制由于忽略了机器人的非线性动力学特性，很难保证机器人控制动力学性能与稳定性，无法满足柔顺装配的要求。此外考虑到在轨装配过程中机器人与被操作物惯性参数不定的特点，传统的控制方法未将其考虑在内，可能导致对准精度差甚至是对准失败的问题。而滑模控制具有响应速度快、抗干扰能力强的特点，因此本小节设计视觉伺服的滑模控制器，能够有效克服机器人运动学、动力学参数不确定性和负载惯性参数不定带来的干扰，保证机器人快速有效的完成伺服对准。

在轨装配机器人动力学模型

(17)

式中：H(q)为正定质量惯性矩阵；C(q)为科氏力与离心力项；τ为机器人关节力矩；Fe为机器人进行在轨装配操作时末端输出力。

当不知道机器人的惯性参数以及末端输出力的大小时，根据计算力矩法，取控制律为

(18)

(19)

即

(20)

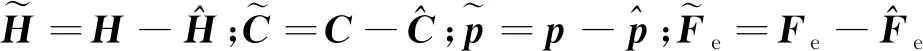
(21)

定义

(22)

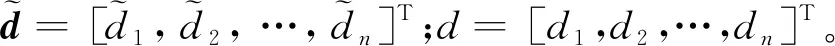
定义滑模控制的滑模面为

(23)

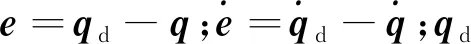
(24)

取

(25)

式中：d为待设计的向量，则

(26)

选取

(27)

式中：η为正定矩阵。则

(28)

由此可以证明，整个控制系统可以从任意初始状态趋向滑模面，满足滑模可达性。

由式(18)和式(25)得无标定视觉伺服滑模控制律为

(29)

4 无标定视觉伺服系统

搭建在轨装配机器人的无标定闭环伺服控制系统：以桁架接口的期望图像特征与图像处理所获得实际特征作为控制系统的输入，利用深度估计器获取当前目标特征点的深度信息，完成图像雅可比矩阵的在线辨识。在此基础上得到下一时刻机器人期望的关节运动，将其输入到视觉伺服系统滑模控制器中以驱动机器人运动。搭载在机器人末端的相机再将得到的图像信息反馈回伺服控制系统，与期望图像特征作对比指导机器人完成桁架的跟踪对准。整个控制系统框图如图1所示。

图1 无标定伺服控制系统框图

定义无标定视觉伺服对准系统误差为

ef(t)=fd(t)-fg(t)

(30)

(31)

将控制量离散化，得到k时刻最优控制量为

u(k)=Δr(k+1)=r(k+1)-r(k)

(32)

式中：r(k)为k时刻相机在任务空间内的坐标参数。

为消除系统跟踪静差，同时克服图像处理时延对桁架跟踪对准性能的影响，引入PI控制策略

(33)

式中：cp、ci分别为PI控制器的比例和积分系数。

5 仿真校验

为了验证所提出的机器人在轨装配无标定视觉伺服对准方法的正确性，利用MATLAB软件对其进行仿真验证。通过2组不同深度信息下特征点在图像空间的运动轨迹与所提方法的仿真结果作对比，验证深度估计器的有效性。接着，通过在机器人系统和被操作物惯性参数不定情况下对引入滑模控制与未引入滑模控制作对比，验证引入滑模控制后对控制精度和控制性能的提升。仿真所用为6自由度机器人，DH参数如表1所示。

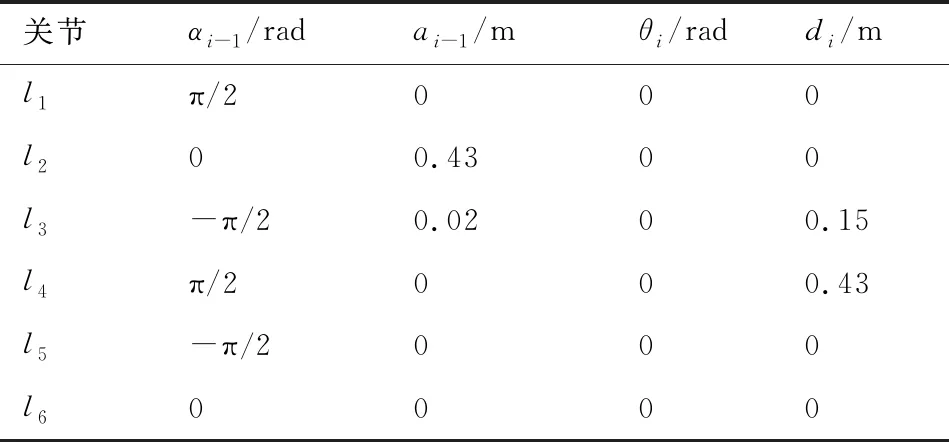
表1 机器人DH参数

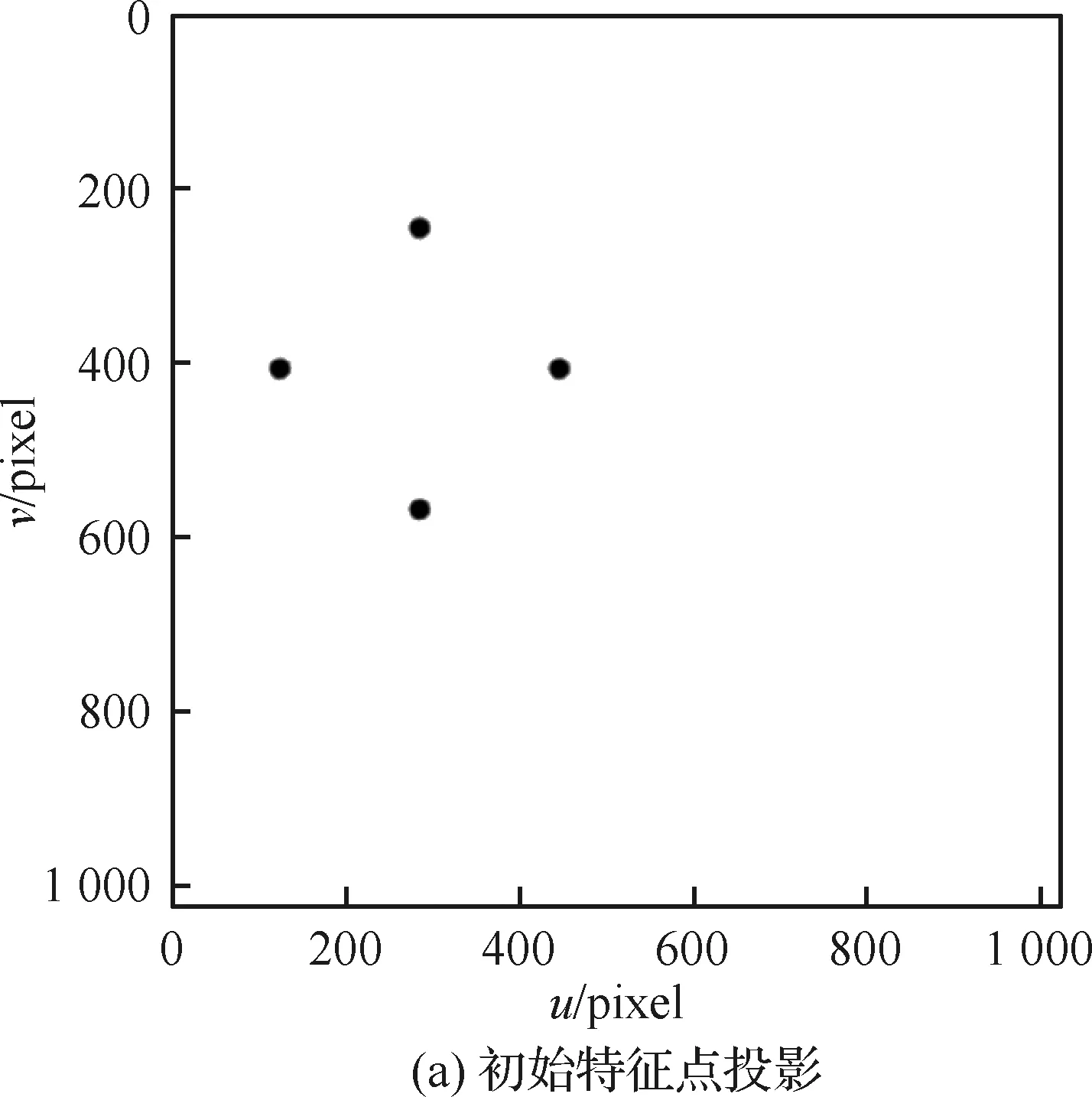
图2 特征点投影变化情况

图3 机器人姿态变化情况

下面将通过2组不同深度信息下特征点的运动轨迹与所提方法作对比：图4(a)为采用所设计的伺服对准控制方法得到的接口特征点的运动轨迹图；图4(b)和图4(c)分别为假设深度信息z=1 m和z=10 m其他条件相同时得到的接口特征点的运动轨迹图。

图4 不同情况下特征点在图像空间的运动轨迹

通过对比可以看出：采用所设计的伺服对准控制方法得到的特征点运动轨迹收敛速度快、运动过程平滑、运动距离最优，特征点在图像空间的运动轨迹明显优于其他两种情况。尤其是z=10 m时的运动轨迹收敛速度很慢且不再是直线。这是因为该情况下图像雅可比矩阵无法很好的近似相机运动与图像特征点运动之间的关系，在相机指引下的机器人每步运动误差都较大，因此特征点的运动轨迹形成了一个锯齿状的路径。而z=1 m时的运动轨迹明显要比z=10 m时的好，这是因为相比于实际深度信息(z=1.3 m)z=1 m比z=10 m的误差更小，更接近于实际深度，因此收敛性要更好。

图5为各个接口特征点的实际深度信息与估计深度信息的变化曲线。从图中可以看出，估计深度在4 s内迅速上升，然后跟踪到实际目标的深度，之后就能在控制器收敛过程中准确跟踪真实深度。由于初始阶段深度信息估计值与实际值相差较大，此时图像雅可比矩阵不能很好的表示相机运动与图像特征点运动之间的关系，从运动轨迹图可以看出特征点的运动方向是有偏差的。

图5 深度估计值与真实值对比

下面将通过在机器人系统和被操作物惯性参数不定情况下对引入滑模控制与未引入作对比：图6(a)为机器人与负载参数未定时采用引入滑模控制方法得到的特征点运动误差图；图6(b)则为未引入滑模控制得到的特征点的运动误差图。通过对比两图可以看出：引入滑模控制后特征点的图像误差在5 s内迅速趋于0，在8 s时所有误差都稳定在0附近。最终的特征点误差数量级为10-8pixel。而传统的控制方法会导致接口4个特征点产生较大偏差，峰值的误差为127 pixel远大于所设计控制方法的峰值误差。在8 s时各特征点基本可以实现稳定跟踪，但仍存在2 pixel误差。得益于无标定视觉伺服闭环特性，最终在10 s时各个特征点的误差都趋于0，但相比于所设计的控制方法收敛速度要慢的多。由此可以证明引入的视觉伺服滑模控制器能实现在轨装配中对接口目标的快速稳定的对准跟踪。