基于Kriging代理模型的约束差分进化算法
2021-07-07叶年辉龙腾武宇飞唐亦帆史人赫
叶年辉,龙腾,2,武宇飞,唐亦帆,史人赫
1. 北京理工大学 宇航学院,北京 100081
2. 北京理工大学 飞行器动力学与控制教育部重点实验室,北京 100081
3. 清华大学 航天航空学院,北京 100084
进化算法通过模拟某些自然界的现象或过程,如变异、繁殖、遗传重组、优胜劣汰等操作,充分探索设计空间,快速高效地求解优化问题。与传统的优化算法(如牛顿法、共轭梯度法等)相比,进化算法无需利用目标函数的梯度信息,运用范围更广泛,但在进化过程中需要消耗大量的计算资源。在几种典型的进化算法中,相比于粒子群优化(Particle Swarm Optimization,PSO)算法、遗传算法(Genetic Algorithm,GA),差分进化(Differential Evolution,DE)算法在鲁棒性、算法控制参数规模等方面具有显著优势[1-2]。此外,为提升差分进化算法的约束处理能力,国内外学者提出了众多约束差分进化算法,主要包括:约束差分进化算法((μ+λ)-Constrained Differential Evolution,(μ+λ)-CDE)[3]、基于ε等级比较机制的差分进化算法[4]、种群协同差分进化算法[5]等。
日益广泛应用的高精度分析模型(计算流体力学、结构有限元、计算电磁学等)不断增加飞行器设计优化问题的计算复杂性,导致差分进化算法难以高效地求解现代飞行器设计优化问题。以全电推卫星平台设计优化问题为例,结构有限元、轨道转移动力学等模型的使用,提高了设计可信度与设计质量,但单次仿真计算成本大大增加,导致设计优化过程计算十分耗时[6]。为了提高计算效率,代理模型(Surrogate或Metamodel)广泛应用于工程设计优化。文献[7-8]从近似精度、鲁棒性、时效性与软件实现难度几个方面,对多项式响应面(Polynomial Response Surface Method,PRSM)[9]、径向基函数(Radial Basis Function,RBF)[10]、Kriging代理模型(KRG)[10]和人工神经网络[11]的综合性能进行了对比研究。研究结果表明,KRG的综合性能相较于其他代理模型具有显著优势。文献[12-13]对KRG代理模型及其优化方法的最新研究进行了全面的介绍,指出目前KRG近似理论研究主要方向包括梯度增强的KRG模型[14]、CoKriging模型[15]、分层KRG模型[16]等。此外,由于KRG可以提供任意点的预测方差,在基于KRG的近似优化方法领域发展了多种优化加点策略,包括期望改善度准则[17]、改善概率准则[18]、均方差准则[12]等。
在代理模型理论基础上,基于代理模型的进化算法(Surrogate Assisted Evolution Algorithms,SAEAs)近年来得以不断发展[19-20]。SAEAs的基本思想是在进化过程中通过进化操作生成后代种群,并利用代理模型预测后代种群的目标函数值,减少对原分析模型的调用次数;同时根据后代种群信息选取部分后代个体作为新增样本点,在种群进化同时动态更新代理模型。目前,SAEAs研究主要关注于求解无约束优化问题。陶良波[21]提出了一种基于双层多代理模型的粒子群优化算法,利用期望改善度(Expected Improvement, EI)准则与混合代理模型,提高了求解低维无约束优化问题(设计变量个数不超过20)的全局收敛性。Liu等[22]结合降维技术提出了一种基于高斯过程的进化算法(Gaussian Process Surrogate Model Assisted Evolutionary algorithm, GPEME),降低了中低维度(设计变量个数在20~50之间)无约束优化问题复杂程度。Yu等[23]在经典PSO算法中结合社会PSO算法,提出了一种基于代理模型的分层粒子群算法,提高了算法对高维无约束优化问题(设计变量个数超过50)的局部搜索能力。田杰等[24]提出了一种基于多目标加点规则的高斯过程模型辅助社会粒子群算法,结合EI准则与统计下限最小准则选取新增样本点,与GPEME相比在高维问题上具有更好的全局收敛性。然而目前面向约束优化问题的SAEAs的研究较少,导致SAEAs在实际工程中的应用受到限制。Wang等[25]利用差分进化分别选取全局与新增搜索样本,提出了一种基于进化采样的优化方法,并结合罚函数方法成功应用于翼型优化问题中。然而,基于罚函数的约束处理方法存在罚系数选取困难的问题,若罚系数选取不当,将造成收敛速度下降甚至无法找到可行改善解。为避免罚系数选取问题,Wang等[26]提出了一种基于全局与局部代理模型的差分进化(Global and Local Surrogate Assisted Differential Evolution, GLoSADE)算法,在全局探索过程中引入可行准则进行个体比较,并利用内点法对种群所有个体进行局部优化,在一定的计算资源情况下可有效求解约束优化问题。然而,该方法每代均需要反复调用原分析模型重估种群,造成计算效率低下、收敛速度缓慢。
为了提高SAEAs在求解飞行器等约束优化问题的计算效率与全局收敛性,本文提出了一种基于KRG代理模型的约束差分进化算法(Kriging assisted Constrained Differential Evolution, KRG-CDE)。通过差分进化操作进行全局探索,并结合约束改善概率与最优适应度选取探索样本,降低代理模型近似误差导致优化性能下降的风险。通过序列二次规划进行局部搜索生成搜索样本,提高种群收敛速度。最后,通过标准测试算例与全电推卫星多学科设计优化问题与国际同类算法进行对比研究,验证了KRG-CDE算法的有效性与工程实用性。
1 基本算法介绍
1.1 差分进化算法
差分进化算法是一种常见的随机搜索算法,通过变异、交叉以及选择操作在进化过程中不断提高种群适应度,逐渐收敛至优化问题最优解附近[1]。
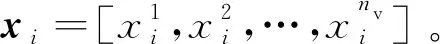

表1 常用变异策略
由交叉操作将xi与对应的vi进行交叉,生成试验个体ui,即
j=1,2,…,nv
(1)
式中:CR为变异概率;jrand为属于[1,d]的随机整数;rj为在[0, 1]内服从均匀分布的随机数。最后,通过选择操作比较xi与ui,选取目标函数值较小者作为下一代父代个体。
1.2 KRG代理模型
KRG代理模型是一种估计方差最小的无偏最优估计插值模型,由全局模型和局部偏差叠加而成[7]。KRG方法的数学表达式为
(2)
式中:μ(x)是设计空间内全局的近似模型,反映原分析模型在设计空间内的总体变化趋势。局部偏差项Z(x)是均值为0、方差为σ2、协方差非零的随机过程,表征在全局近似模型基础上的局部偏差,其协方差矩阵与相关函数为
(3)
μ与σ2的最小二乘估计值可根据式(4)得到
(4)
式中:I为NKRG个元素的单位行向量。KRG方法的具体描述可参考文献[7, 10]。
1.3 径向基函数
RBF是一种插值型代理模型,可表示为径向函数线性加权形式:
(5)
其中,权重系数矢量w可由式(6)求解得到
(6)
式中:NRBF为构造RBF代理模型的样本规模。文献[27]指出选用三次函数作为径向函数的RBF代理模型具有更好的近似性能,因此本文中径向函数为三次函数,即φ(r)=r3。
2 KRG-CDE算法描述
一般的约束工程优化问题的数学模型可描述为
(7)
式中:nv为优化问题维度;f为目标函数;gj为第j个约束函数;xLB与xUB分别为设计变量下界与上界。
2.1 算法优化框架
KRG-CDE算法的流程如图1所示,主要分为全局探索与局部搜索两个阶段:在全局探索阶段,通过KRG代理模型提供的预测方差,构建基于约束改善度与最优适应度的可行准则,从而引导种群向可能存在最优解但样本较为稀疏的区域进化;在局部搜索阶段,为了有效折中代理模型的鲁棒性、近似精度与构造效率[8],采用RBF构造局部优化问题并结合序列二次规划方法求解,从而提高算法的收敛速度。KRG-CDE算法的具体步骤如下。
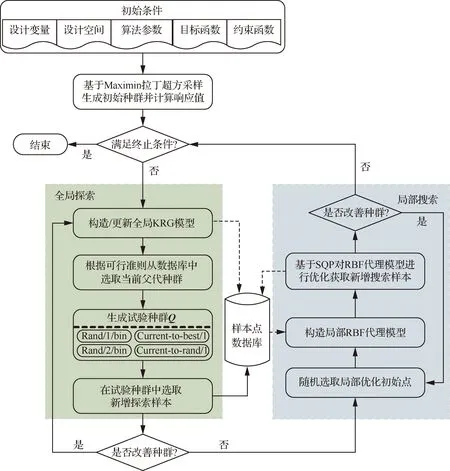
图1 KRG-CDE算法流程图
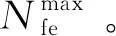
步骤2采用基于Maximin的拉丁超方试验设计方法,在初始设计空间内生成NP个初始样本点。以最小距离最大化作为空间均布性评价指标,即
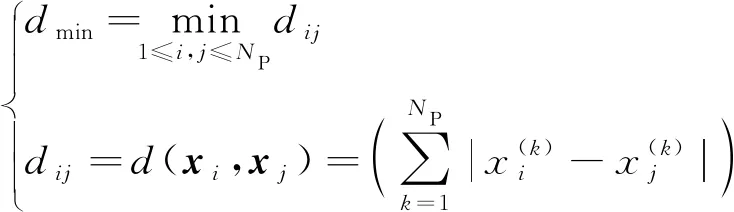
(8)
随机生成50组拉丁超方采样方案,并选取其中空间均布性最优的方案作为初始样本点。计算初始样本点的相应的真实目标、约束函数值,并初始化样本点数据库。
步骤3利用样本点数据库中所有样本点及函数响应值对目标函数及各个约束函数构造KRG代理模型。
步骤4根据式(9)计算样本点数据库中所有样本点的约束违背度。根据可行准则对当前样本点数据库进行排序,并从中选取前Np个个体作为当前的父代种群。
(9)
步骤5分别采用Rand/1/bin、Rand/2/bin、Current-to-rand/1以及Current-to-best/1变异算子与交叉算子生成试验种群Q={QR1∪QR2∪QCtoR∪QCtoB},其中采用Current-to-rand/1以及Current-to-best/1算子生成的变异种群不进行交叉操作直接作为试验种群QCtoR与QCtoB。
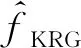
(10)
式中:NKRG为构造KRG代理模型的样本规模。
步骤7根据改进的可行准则从试验种群中选取新增探索样本,具体介绍参见2.2节。计算新增探索样本的真实目标函数与约束函数值并将其添加至样本点数据库中。基于可行准则判断新增探索样本点是否改善当前种群。若种群得到改善,返回步骤3,否则执行步骤8。
步骤8从当前种群中随机选取某个体作为序列二次规划方法的初始点。根据欧氏距离从样本点数据库中选取距离初始点较近的NRBF个样本点分别构造目标函数与约束函数对应的局部RBF代理模型。构造RBF的样本点规模与优化问题的维度相关,计算公式为
(11)
当NRBF大于已有数据库样本规模时,采用数据库中所有样本点构造RBF代理模型。
步骤9根据构造RBF的样本点建立局部优化数学模型如式(12)所示,并采用序列二次规划方法求解该优化问题得到新增搜索样本点。
(12)
步骤10计算新增搜索样本的真实目标函数与约束函数值并将其添加至样本点数据库中。基于可行准则判断新增搜索样本是否改善当前种群。若种群得到改善,返回步骤8,否则执行步骤11。
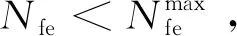
2.2 基于约束改善度与最优适应度的可行准则
在处理约束优化问题时,进化算法通常采用可行准则[28]对种群进行排序或比较。可行准则的比较标准如下:可行个体优于非可行个体;非可行个体间比较时,约束违背度较小的个体更优;可行个体间比较时,目标函数值较小的个体更优。
然而,在求解非线性程度较强的约束优化问题时,代理模型对目标函数以及约束函数的预测精度难以保证,进而影响传统可行准则个体排序结果的可靠性,最终导致种群向错误的方向进化。因此,本文提出了一种基于约束改善度与最优适应度的可行准则。种群不存在可行个体时,利用各约束的改善概率[18]代替约束违背度选取新增探索样本;种群存在可行个体时,构建最优适应度函数选取探索样本,具体步骤如下。
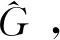
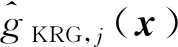
(13)
(14)
步骤3根据式(15)计算可行种群Qfeasi的最优适应度函数。
(15)
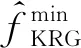
3 算法性能测试
为验证KRG-CDE算法求解约束优化问题的全局收敛性与优化效率,本文选取了12个约束优化问题作为标准测试算例,并与GLoSADE算法[26]以及(μ+λ)-CDE算法进行对比。
3.1 测试问题描述
选取的标准测试算例的基本信息如表2所示[29-30]。标准测试问题的目标函数与约束函数的具体表达式见文献[29-30]。其中包括两个工程标准测试算例,压力容器设计问题(Pressure Vessel Design, PVD4)和齿轮减速箱优化问题(Speed Reducer design, SR7)。
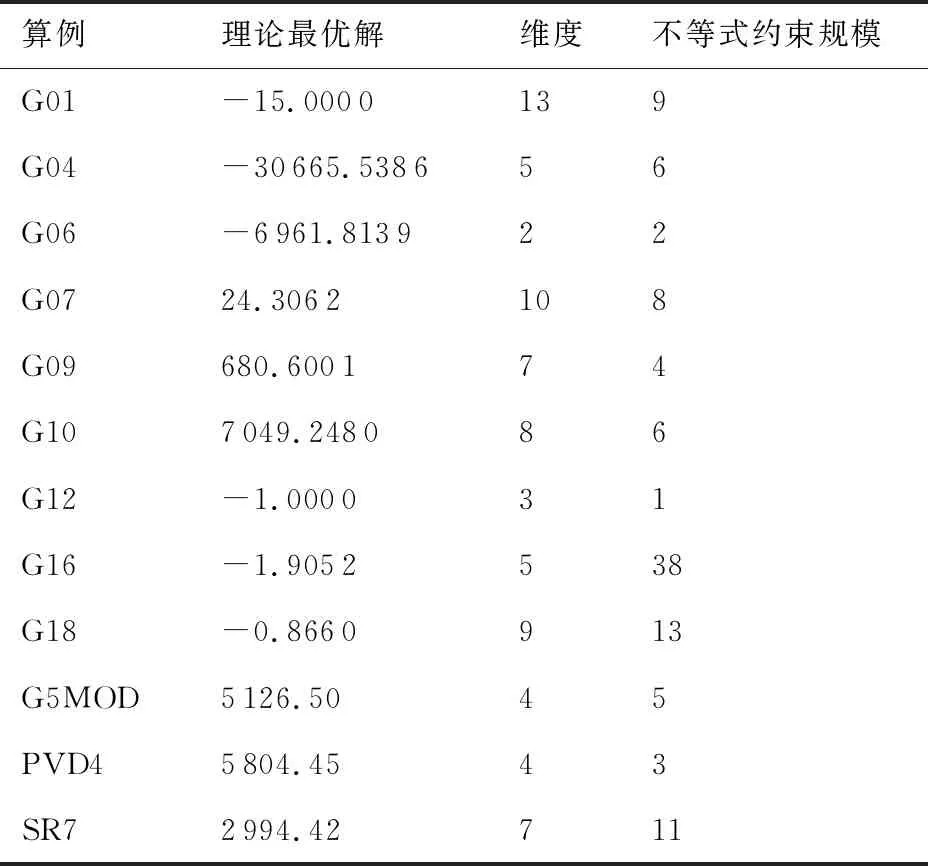
表2 标准测试算例基本信息
3.2 算法参数设置
KRG-CDE算法的参数设置如表3所示。GLoSADE算法[26]为典型约束SAEA,其最大模型调用次数设为400。(μ+λ)-CDE算法[3]是一种能够有效求解约束优化问题的差分进化算法,其最大模型调用次数设为3 000。两种算法的其余参数均与原始文献参数设置一致。为了减少随机误差影响,各算法分别对各算例连续优化25次,统计优化结果中可行解的最优解(Best)、均值(Mean)、最差解(Worst)、标准差(Std)以及可行次数(FeasiNum)进行对比。

表3 KRG-CDE算法参数设置
3.3 优化结果对比分析
分别采用KRG-CDE、GLoSADE与(μ+λ)-CDE算法求解上述约束优化问题,优化结果如表4所示,优化结果箱线图如图2所示。

图2 KRG-CDE、(μ+λ)-CDE与GLoSADE算法优化结果缺口箱线图
结果表明,与无代理模型辅助的约束差分进化算法(μ+λ)-CDE相比,KRG-CDE算法可在较少的计算资源条件下使种群进化至理论可行最优解附近区域。以G01约束优化问题为例,KRG-CDE算法的计算效率与(μ+λ)-CDE算法相比提高了90%,且优化结果均值与理论可行最优解的相对误差仅为0.31%,而(μ+λ)-CDE算法仍未找到理论最优解附近区域。对于可行域极小的约束优化问题G18(可行域占设计空间比例小于0.000 1%[29]),KRG-CDE算法在有限的计算资源条件下均能够找到可行解,然而(μ+λ)-CDE算法在充足的计算资源条件下仍无法找到可行解。
与国际同类的GLoSADE算法相比,KRG-CDE的全局收敛性与计算效率均具有显著的优势。以G06约束优化问题为例,KRG-CDE算法在300次模型调用次数以内均能够找到理论可行最优解,然而GLoSADE在400次模型调用次数的条件下,仍未能够找到理论最优解附近区域。对于可行域极小的G18测试算例,GLoSADE在25次优化中仅17次找到可行解,而KRG-CDE算法25次优化结果均为可行解,进一步验证了KRG-CDE的寻优能力。由箱线图结果可知,除G01、PVD4问题外,对于大多数标准测试算例,KRG-CDE算法均具有更好的鲁棒性,并且其优化结果分布更加接近理论最优解。
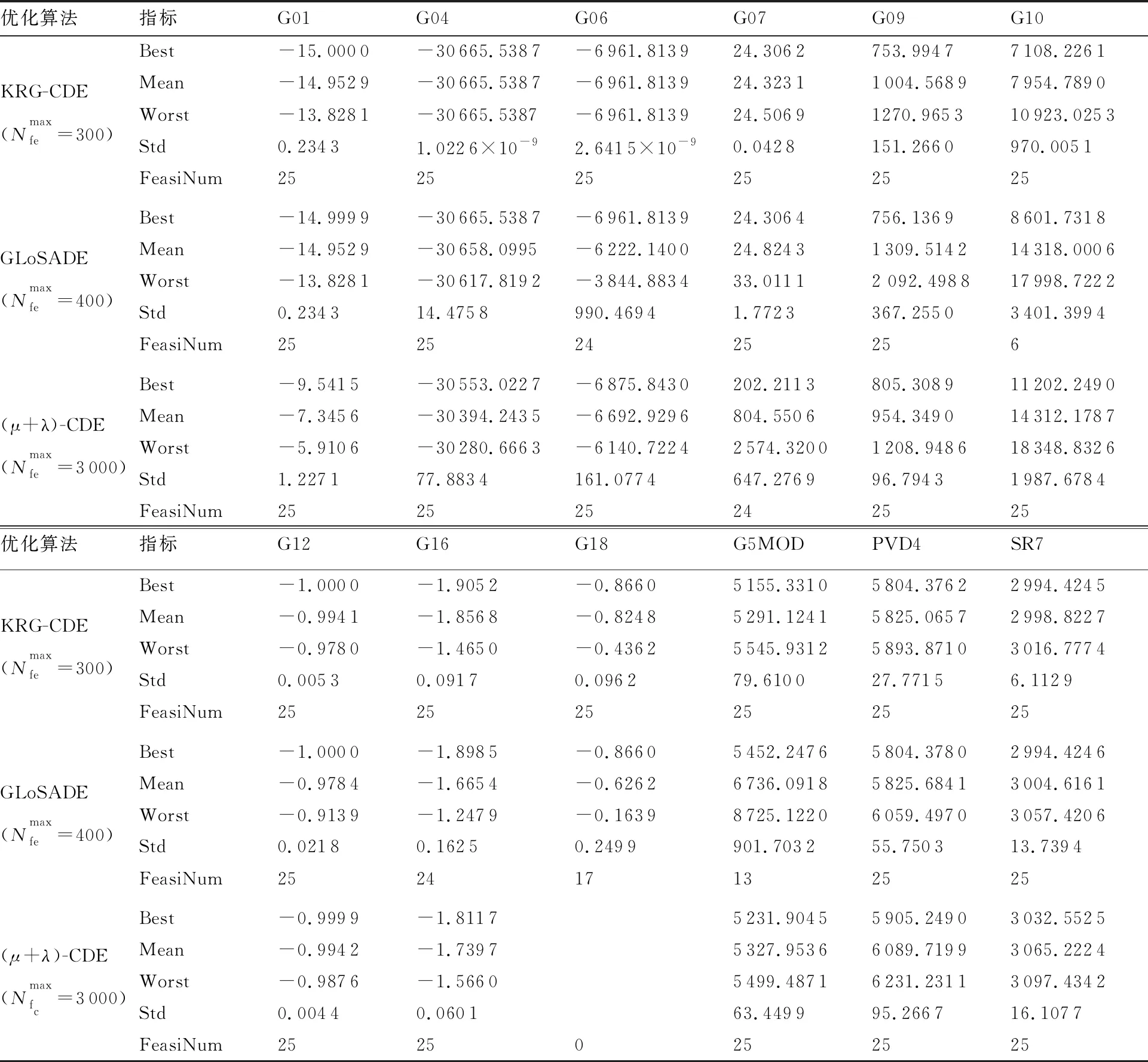
表4 KRG-CDE,(μ+λ)-CDE与GLoSADE算法优化结果
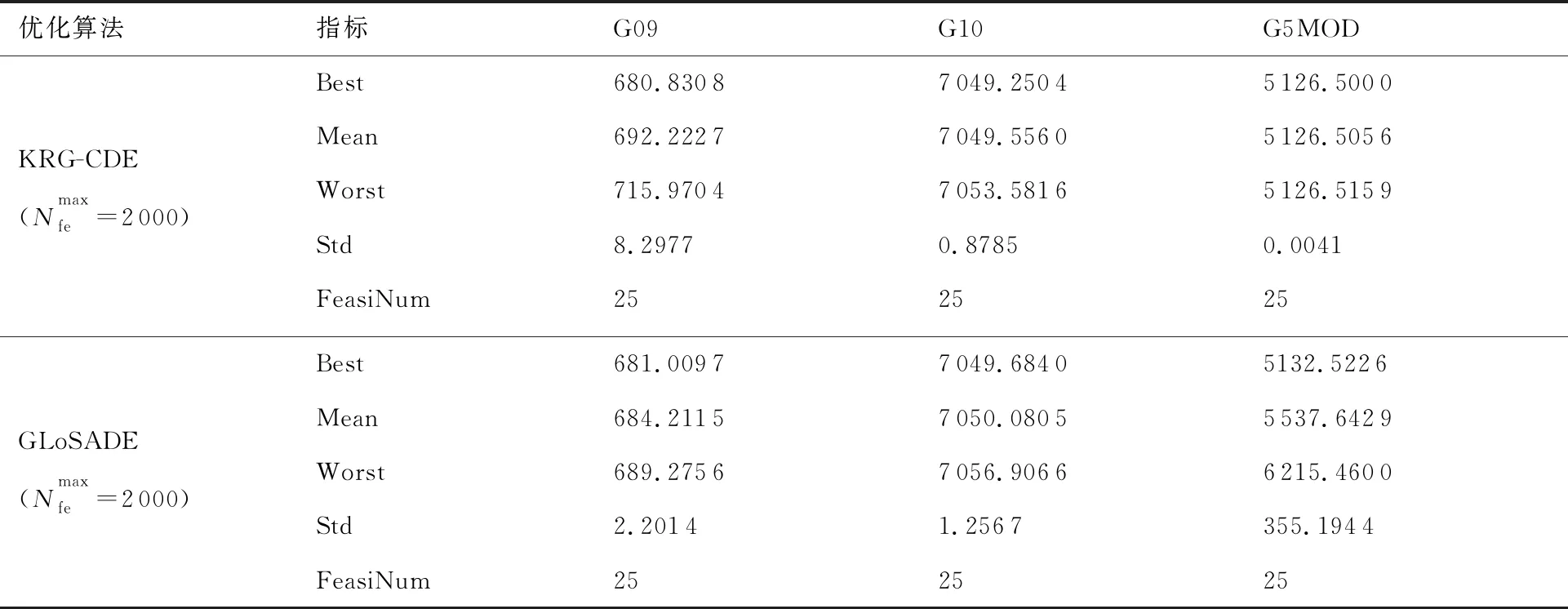
表5 2 000次模型调用下的优化结果对比
由上述优化结果可知,本文提出的KRG-CDE算法在全局收敛性、鲁棒性以及优化效率上具有显著优势。
4 全电推卫星多学科设计优化实例
本节将KRG-CDE算法应用于全电推卫星多学科设计优化(Multidisciplinary Design Optimization, MDO)问题[6],并与GLoSADE、(μ+λ)-CDE算法进行对比。全电推卫星是一个典型的高维多学科耦合系统[31],其多学科分析过程需要通过迭代求解保证学科相容性。此外,全电推卫星MDO问题涉及多个高耗时学科分析模型(有限元模型以及轨道转移动力学模型等),进一步加剧了计算复杂性。本文提出的KRG-CDE求解全电推卫星MDO问题,从而验证本文提出算法的工程适用性。
4.1 优化问题描述
全电推卫星MDO问题旨在通过调整推力器安装位置、GTO轨道推力角等参数,在满足位保精度、结构弯曲频率等约束的前提下降低整星发射质量。该优化问题涉及15个设计变量与11个约束条件,优化模型数学表达式如下[6]:
findX=[α,β,φ,dT,dN,Asa,Cb,Ar,
Hw,HS,HC,HM,PS,PC,PM]T
(16)
式中:相关变量定义详见文献[6];mi为第i个学科的质量;MS为全电推进卫星发射质量,即为优化的目标函数。
4.2 算法参数设置
KRG-CDE算法与GLoSADE算法最大分析模型调用次数设为200以及500次,其余参数保持不变。(μ+λ)-CDE的最大分析模型调用次数设为1 000。
4.3 优化结果对比分析
KRG-CDE算法的优化收敛情况如图3所示,可以看出,虽然初始种群中未存在可行解,KRG-CDE算法仍然能够在优化初期找到可行解。此外,KRG-CDE算法在优化过程中保证了优化结果可行性,同时持续改善卫星的整星质量。
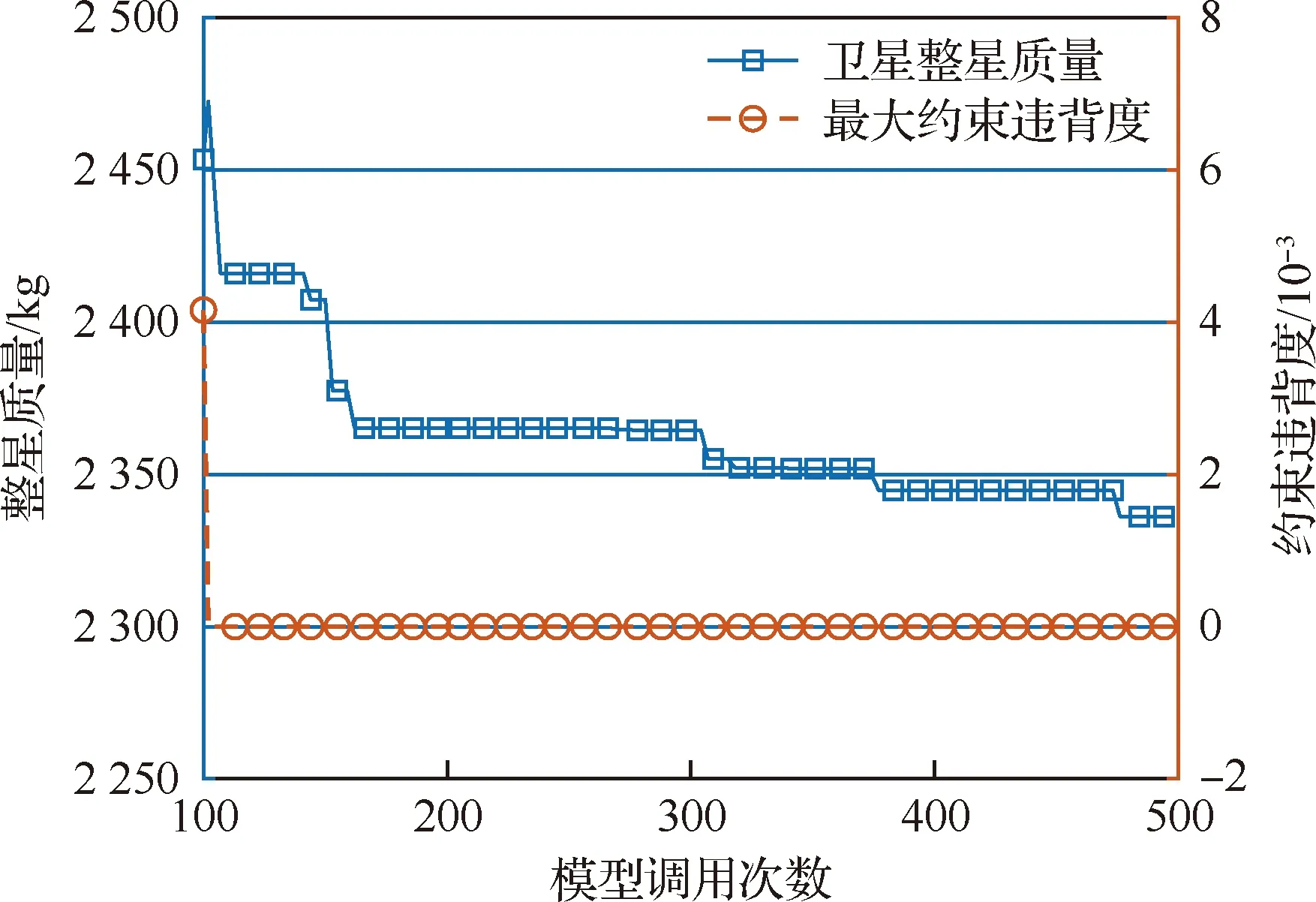
图3 KRG-CDE算法全电推卫星MDO问题收敛曲线
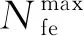
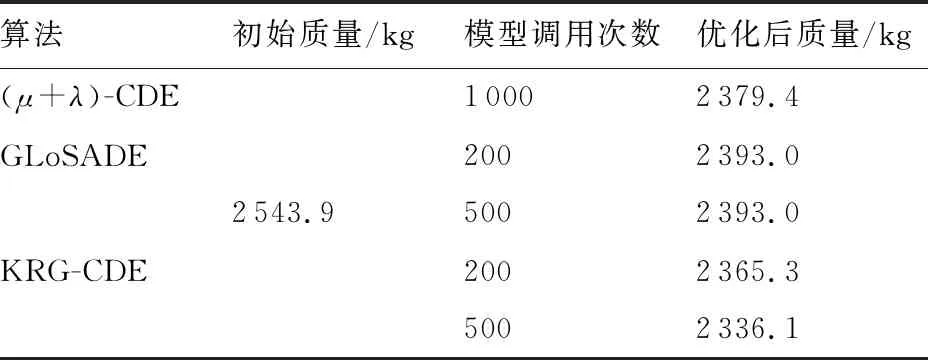
表6 全电推卫星MDO问题优化结果目标函数值
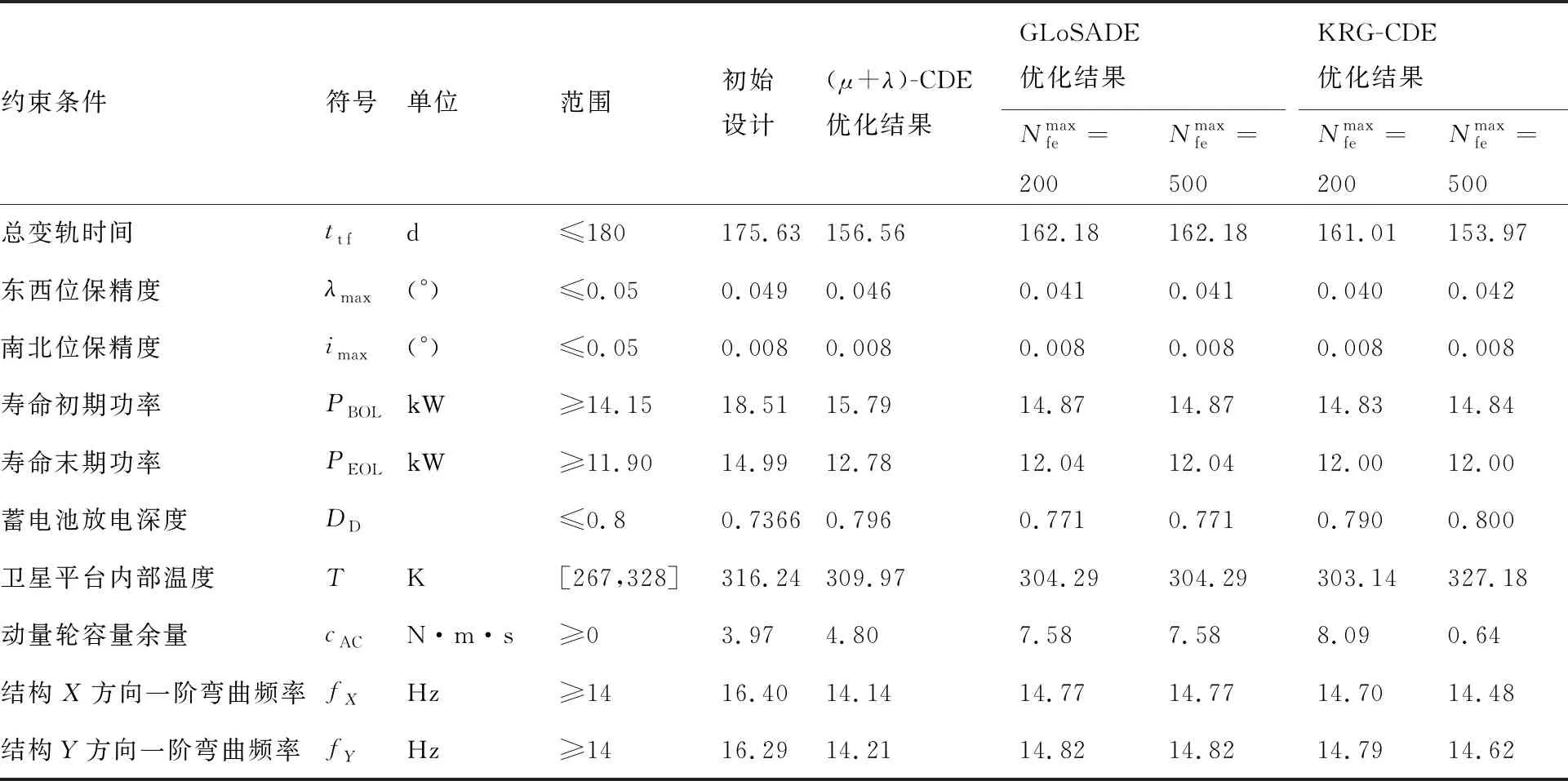
表7 全电推卫星MDO问题优化结果约束函数值
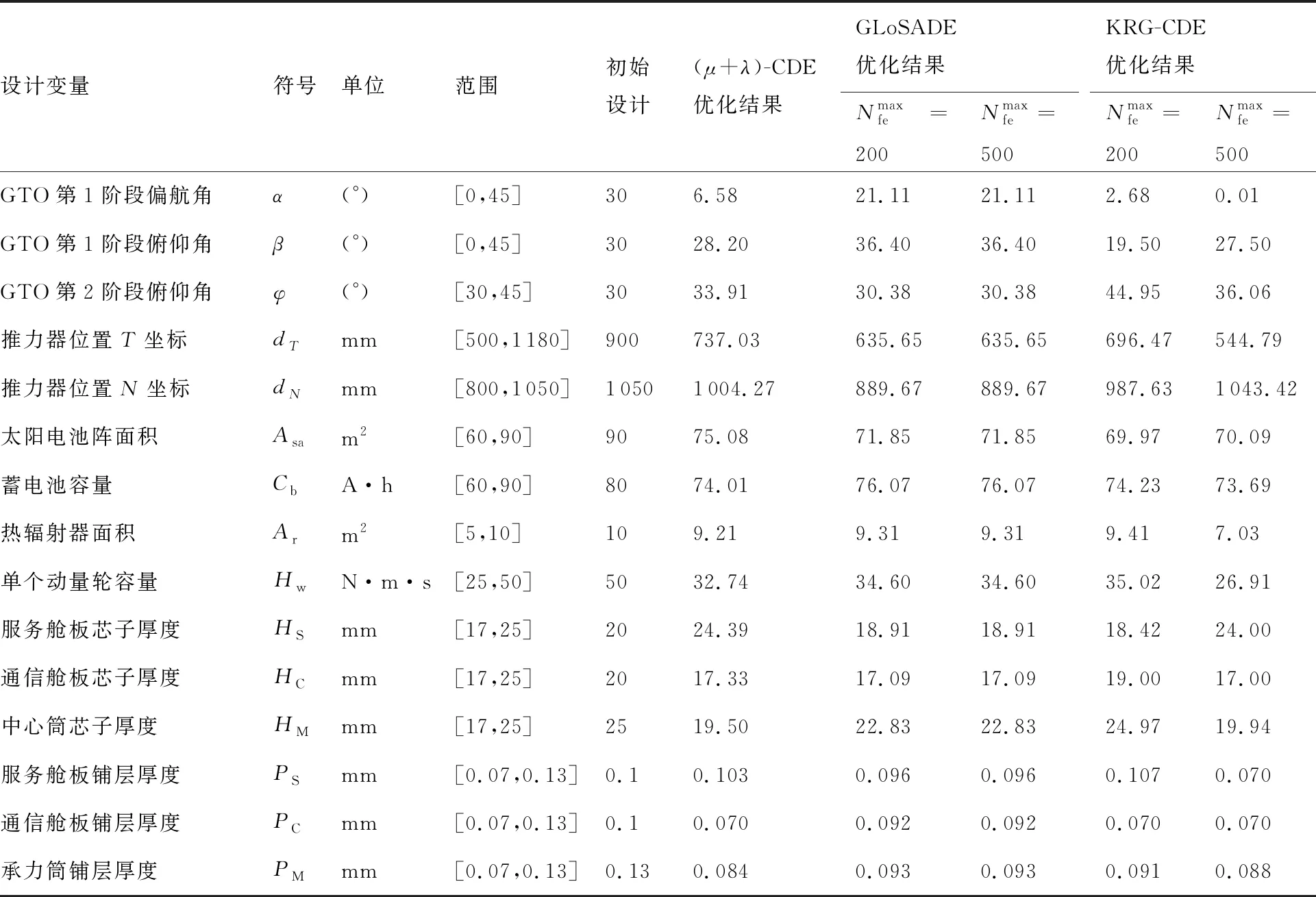
表8 全电推卫星MDO问题优化结果设计变量
5 结 论
1) 针对现有SAEAs难以求解复杂约束优化问题,本文提出了一种基于KRG代理模型的约束差分进化算法KRG-CDE,进一步提高了约束问题的优化效率。
2) 结合了约束改善概率与最优适应度,提出了一种改进的可行准则,提高新增样本点的潜在最优性与可行性,进而提升算法的全局收敛性。
3) 标准测试算例与全电推卫星多学科优化实例的优化结果表明,KRG-CDE算法与GLoSADE、(μ+λ)-CDE算法相比,在全局收敛性以及计算效率方面具有显著优势。
4) 未来将进一步探索基于代理模型的其他智能优化算法(包括遗传算法、粒子群算法等),并将本文提出的算法应用到更多的飞行器优化设计实例当中。
