基于多目标帝国竞争算法的进场排序与调度
2021-07-07张军峰游录宝杨春苇胡荣
张军峰,游录宝,杨春苇,胡荣
南京航空航天大学 民航学院,南京 210016
空中交通需求的持续增长与可用空域资源的长期受限,给空中交通管理(Air Traffic Management,ATM)带来了新的机遇与挑战。以中国繁忙机场的终端区运行为例,完全依赖于管制员指令引导的方式,容易导致管制工作负荷激增、机场运行效率降低、环境影响问题突出。因此,如何有效地优化和调度时空资源,成为空中交通管理领域的研究热点,而进场排序与调度是该领域的典型问题。
进场排序与调度旨在不违反安全间隔的条件下,结合运行约束,合理高效地为进场航空器分配着陆跑道,提供最优着陆次序与时间,以期达到提升跑道容量、减少延误、缓解管制工作负荷的目的[1]。历经近30年,进场排序与调度的研究涵盖了静态优化[2]与动态优化[3],确定型优化[4]与随机型优化[5]、单阶段优化[6](直接优化着陆时间)与两阶段优化[7-8](先确定着陆次序再优化着陆时间)、是否提供相应管制建议[9](即优化时间的可达性)等方面,其求解工具或算法包括:CPLEX[1,7]、分支定界[5]、动态规划[6]、模拟退火[10]、遗传算法[11]、粒子群算法[12]等。
对于进场排序与调度问题,各利益相关方秉持不同的诉求:空管立足运行安全,航司着眼效率优先,机场注重容量增强,民众关切准点运行与环境影响。因此,近年来进场排序与调度的研究重点由单目标优化逐步转向多目标优化。Sam等[13]研究了具有不同目标函数的进场排序与调度问题,并考察了不同性能指标的解决方案之间的差异。Hong等[14]以总飞行时间和序列变化次数最小化为目标,基于混合整数线性规划对着陆次序和时间进行优化。Zhang等[15]采用基于帕累托支配的多目标模拟退火算法(MOSA),解决了在考虑连续航班运行的条件下,最大化跑道运行能力和最小化飞行延误的进场排序问题。带精英策略的非支配排序遗传算法(NSGA-II)在多目标进场排序与调度研究中应用广泛:Mokhtarimousavi等[16]考虑了跑道容量、地面成本和环境成本,基于NSGA-II实现进场排序与调度的多目标优化;马园园等[17]面向延误时间、延误架次和运行公平性的目标,利用NSGA-II求解多目标进场排序与优化;刘继新等[18]在综合考虑空管、航空公司和机场三方的利益需求下,提出一种时隙交换方法,并基于NSGA-II解决不同交通密度情况下的进场排序与调度问题。
上述多目标优化兼顾了诸多利益相关方的诉求,也丰富了进场排序与调度研究的内涵。然而,仍存在两方面问题亟待解决:① 诸多优化目标之间是否存在冗余,优化目标选择能否找到依据;② 如 何评价多目标优化的解集,能否在常用的NSGA-II之外寻求更为精准和高效的多目标优化求解算法。本文拟通过将进场排序与调度问题等效于机器调度问题,借鉴机器调度领域的研究成果,为多目标进场排序与调度的目标选择提供依据;进一步,引入非支配排序,基于近年来广泛应用的帝国竞争算法[19],设计多目标帝国竞争算法(Multi-Objective Imperialist Competitive Algorithm,MOICA),解决进场排序与调度问题;最后,基于通用数据集与实际运行数据构建仿真验证的场景,一方面考虑帕累托最优解集的评价指标,对比分析本文提出的MOICA与进场排序与调度领域广泛使用的NSGA-II及MOSA,另一方面考察了MOICA在实际管制运行中的优化效能。
1 多目标进场调度模型构建
1.1 问题等效
进场航空器的排序与调度问题可视为机器调度问题[20-21]:跑道为机器,进场航空器为工件,其进入终端空域的时间等效于工件的出现时间,航空器的最早、最晚以及计划到达时刻,分别与工件提交时间、最后期限以及交付时间一一对应,而尾流间隔约束则与顺序决定的准备时间相当。为后续阐述方便,相关变量如表1所示。

表1 变量定义
1.2 目标选择
最小化最大完成时间min(maxCi),表明最后优化一架航空器尽早着陆,意味着跑道运行容量的最大化,该目标是机场的关注点。
最小化最大流动时间min(maxFi),表明最小化进场航空器在终端空域飞行的最长时间,意味着对各个航空公司的航空器实施公平的调度。
最小化最大延误时间min(maxTi),表明最小化进场航空器的最大延误,体现对航空器实施公平调度。
Cmax(S*{max})=max(C(S*{Σ}))
证明如下:
首先,设Cmax(S*{max})>max(C(S*{Σ}))。因为Cmax(S*{max})=max(C(S)),定义S为任意一个调度,而S*{Σ}为S的其中一种情况,所以假设Cmax(S*{max})>max(C(S*{Σ}))不成立。
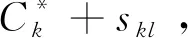
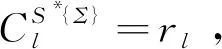
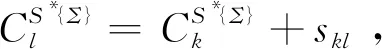
最后,证得推论成立。

1.3 模型构建
基于上述分析,多目标进场优化排序与调度问题可以描述为:对于给定n架进场航空器,当满足着陆时间窗约束、尾流间隔约束、着陆次序的最大位置转换约束等,以最小化进场航空器终端区内的总飞行时间、最小化最大飞行时间、最小化进场航空器的总延误时间为目标,优化进场航空器的着陆序列及时间。构建数学模型如下:
(1a)
(1b)
min maxFi
(1c)
(1d)
(1e)
(1f)
(1g)
(1h)
(1i)
kCPS≤K
(1j)
其中:式(1d)为进场航空器着陆时间的时间窗限制;式(1e)表示着陆次序;式(1f)确保了进场航空器前后机之间的尾流间隔约束;式(1g)与式(1h)表示进场航空器的延误时间定义及约束;式(1i)表示进场航空器在终端空域的飞行时间;式(1j)表示着陆次序调配需要满足的最大位置转换约束。
2 多目标进场调度算法设计
2.1 帝国竞争算法
帝国竞争算法(Imperialist Competitive Algorithm, ICA)[19]是一种社会政治进化算法,该算法将初始解集视为若干个帝国(Emp.),每个帝国由一个殖民国家(Imp.)与若干个殖民地(Col.)组成,其中殖民国家代表该帝国内最优解,通过成本值(Costi=f(Countryi))确定。对于最小化问题,其算法简要流程如下所示:
步骤1初始化。随机产生初始国家集合N,根据成本值选取殖民国家,分配殖民地,组建帝国。
步骤2同化。帝国中的殖民地在一定概率下向殖民国家靠拢。
步骤3革命。帝国中的殖民国家及殖民地在一定概率下发生突变。
步骤4帝国内竞争。更新帝国内殖民国家与殖民地的成本值,成本值最小的成为新的殖民国家。
步骤5帝国间竞争。更新各帝国势力值,将最弱帝国的最弱殖民地转移到最强帝国中。
步骤6帝国消亡。若某帝国中所有殖民地都被掠夺,则此殖民国家沦为殖民地,该帝国消亡。
步骤7验证终止条件。若满足,输出最优殖民国家,否则重复步骤2~步骤6,直到满足终止条件。
帝国竞争算法的优点在于:通过帝国内竞争和帝国间竞争,加强深度搜索和广度搜索,从而提升了邻域搜索和全局优化的能力。
2.2 多目标帝国竞争算法
将帝国竞争算法引入进场排序与调度的多目标优化,相较于传统帝国竞争算法,其特点在于:① 解集的初始化与更新策略;② 面向多目标优化的成本函数的构建;③ 面向多目标优化的帝国势力的衡量。假设多目标帝国竞争算法(MOICA)的最大迭代次数imax,种群数量为npop,殖民国家数量nimp,MOICA的算法流程图如图1所示。
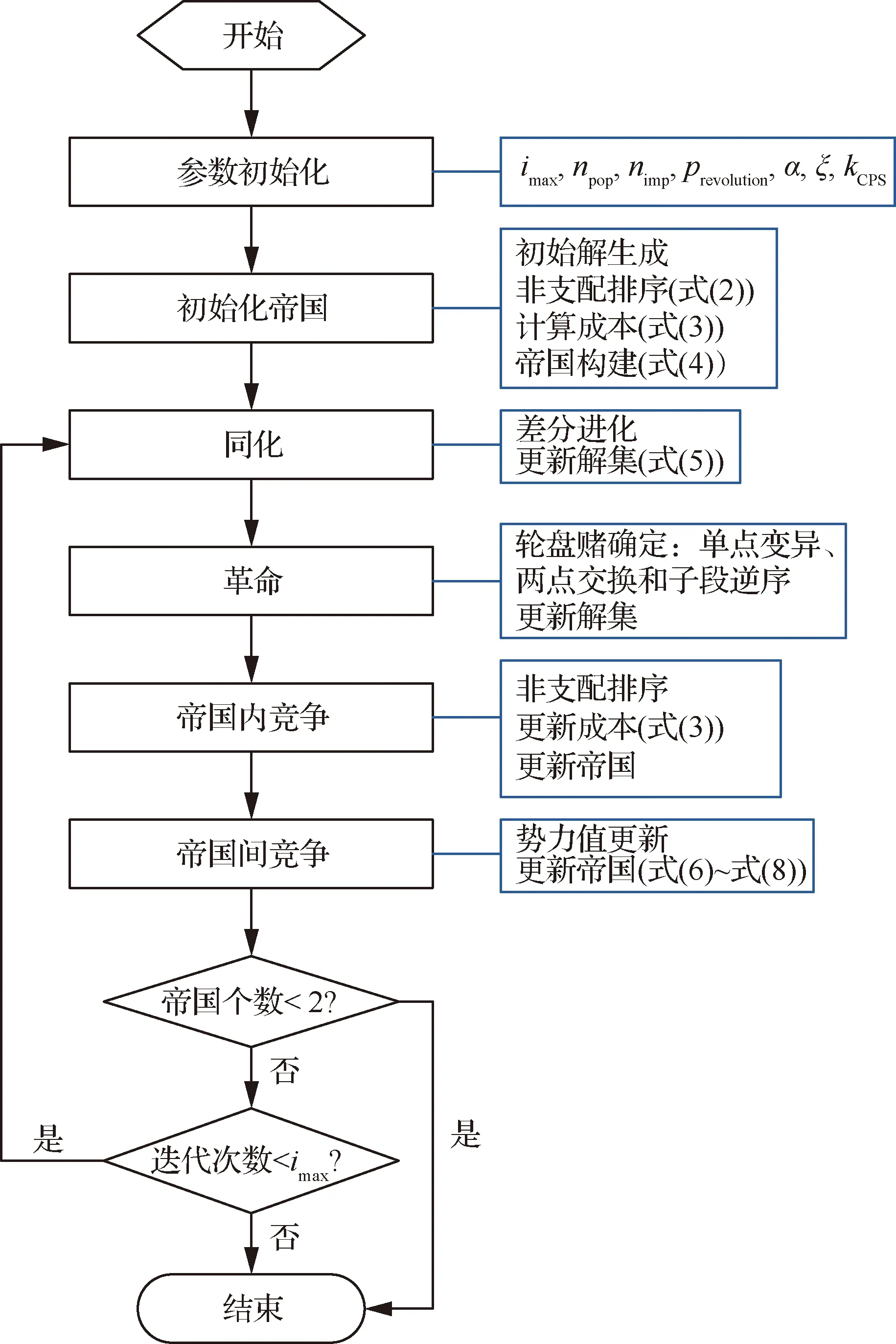
图1 多目标帝国竞争算法流程示意图
1) 初始化帝国
对于进场航空器排序与调度问题,各航空器的优化着陆时间构成一个初始解,即一个国家。生成初始解集时,需要满足时间窗约束(ri,di),本文拟采用线性插值实现解集初始化,如式(2)所示。
Ci=ξdi+(1-ξ)rii∈I
(2)
式中:ξ∈[0,1]。
由于面向多目标优化,常规的基于目标函数构建成本函数的方式并不可行。鉴于此,本文采用非支配排序与拥挤距离实现成本函数的构建,具体包括:
① 基于初始化的解集计算目标函数值,并针对所得的目标值进行快速非支配排序。
(3)
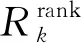
③ 初始化殖民国家,优先从帕累托前沿(Pareto Front,PF)中选取殖民国家,若PF中解的个数小于设定的帝国个数,则从下一层级中依次选择成本值小的解作为补充。
④ 初始化殖民地,采用轮盘赌的方式,利用式(4)将殖民地分配给殖民国家。
(4)
式中:α为选择系数。
如此完成了初始化帝国的工作,每个帝国,即进场排序与调度的初始解集的子集,包含一个PF解和若干个初始解。
2) 同 化
同化过程是帝国内殖民地向殖民国家靠拢的过程,也即进场排序与调度的可行解向帕累托最优解学习的过程。本文采用差分进化的方式,如式(5)所示,实现帝国内的同化。
Col.←Col.+β·rand·(Imp.-Col.)
(5)
式中:β表示差分进化系数;rand为随机数。
3) 革 命
为防止迭代过程中陷入局部最优解,对殖民地进行革命操作,文中主要采用单点变异、两点交换和子段逆序3种算子进行革命。
单点变异算子中,随机选择一个进场航空器,按式(2)分配新的优化着陆时间;两点交换算子中,随机交换两个航空器的优化着陆时间;子段逆序算子中,随机选择一部分航空器的优化降落序列,并逆序。值得注意的是,在实施上述操作需要考虑位置转换约束(Constrained Position Shift, CPS)以及相应的尾流间隔,以确保革命后的解仍是可行解。
4) 帝国内竞争
基于同化和革命的解集更新,计算目标函数值,再次进行快速非支配排序操作,利用式(3)更新国家的成本值。进一步,比较帝国内殖民国家与殖民地的成本,若殖民地的成本优于对应的殖民国家时,那么优秀殖民地成为新的殖民国家,原来殖民国家沦为殖民地。
5) 帝国间竞争
帝国间竞争是各个帝国间殖民地再分配的过程,势力弱小的帝国将被势力强大的帝国逐步吞并,直至消亡。帝国势力值计算过程如下所述:
(6)
Empj.Cost
(7)
(8)
在此过程中,式(6)综合帝国内殖民国家与殖民地的成本计算帝国总成本,其中:μ表示势力值系数; |Empj|表示帝国中殖民地的数目;随后,按照式(7)和式(8)实现势力值的量纲统一,其中式(7)的作用在于防止势力为零的情况,本文λ取值为1.2。
2.3 多目标优化解的评价
如何评价多目标进场排序与调度优化解集的优劣,选择兼顾各利益相关方诉求的优化方案,也是值得深入研究的问题。本文拟从帕累托最优解的收敛性和多样性两个角度出发,通过如下4个指标[23]评估本文提出的多目标帝国竞争算法。
1) 覆盖率 (C-Metric, CM)
覆盖率是衡量帕累托解集收敛性的指标,即
CCM(PFA,PFB)=
(9)
式中:PFA、PFB分别为两组Pareto最优解集。分子表示解集B受解集A支配的解的个数,分母表示解集B中所有解个数。若CCM(PFA,PFB)=1,说明解集B完全受解集A所支配,即解集B收敛性比A差。
2) 空间分布 (SPacing, SP)
空间分布是评估帕累托解集广泛程度的指标,即
(10)
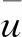
3) 超体积 (Hyper Volume, HV)
超体积是评估帕累托解集收敛性和多样性的综合指标,即
(11)
式中:δ(·)表示勒贝格测度,用来测量体积;Vk表示第k个点与参考点围成的区域超体积。超体积值越大,表明解集越好。
4) 平均理想距离(Mean Ideal Distance, MID)
平均理想距离衡量帕累托解集和理想点之间距离的指标,即
CMID(PF)=
(12)
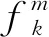
3 仿真验证
仿真验证从2个角度展开,一方面利用进场排序与调度研究领域常用的基准案例——OR数据集(http:∥people.brunel.ac.uk/~mastjjb/jeb/orlib/ airlandinfo.html),考察MOICA的效果,并与多目标进场排序与调度常用的NSGA-II及MOSA进行对比;另一方面采用实际运行数据,验证MOICA的适用性。
MOICA通过MATLAB2014b编程实现,运行环境为:Windows10操作系统,Corei7-7700处理器、3.6 GHz主频和8 GB内存的微机。
3.1 OR数据验证
3.1.1 运行场景
OR数据集中关于进场排序与调度共有13组案例,航空器架次从10~500架不等。由于第1~8组案例不满足进场排序与调度的尾流间隔三角不等式,故采用第9~13组数据,分别有100/150/200/250/500架次航空器,第9~12组数据,构成大规模数据集;拆分第13组数据,构成小规模数据集,拆分的依据在于——进场航空器进入终端空域的时间具有波次效应。进一步,为了反映进场航空器的交通需求特性,引入压缩因子Kd,即
(13)

具体的数据集信息如表2所示,数据集中airland #13.1参数信息详情如图2所示,其中蓝色方框表示航空器进入终端空域时间,黑色星号表示着陆时间窗,红色圆圈表示预计着陆时间。
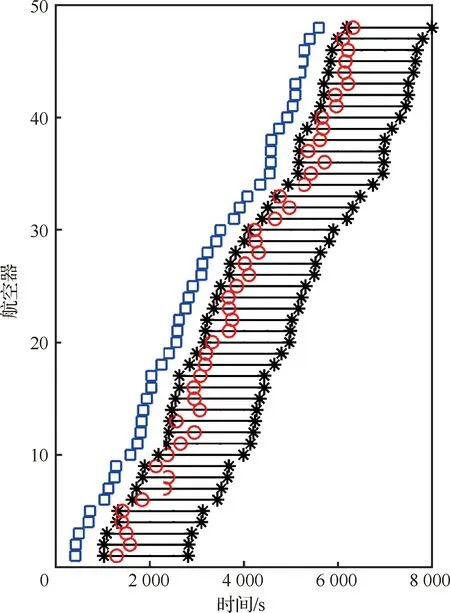
图2 仿真场景示意图
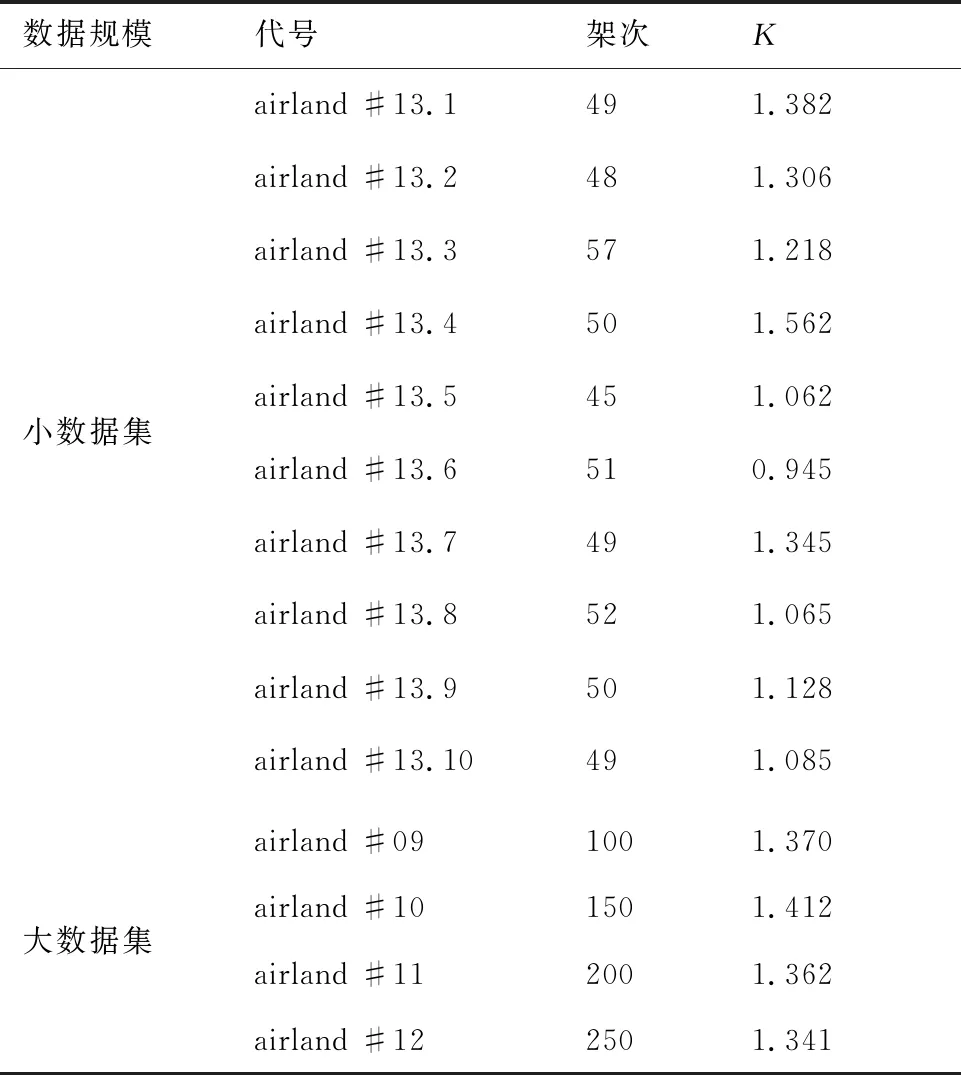
表2 仿真数据集信息
实验中:MOICA应用于大规模数据集时,imax=250、npop=100、nimp=7;应用小规模数据集时,imax=150、npop=75、nimp=5;革命概率选为0.35,选择系数为0.9,同化系数为2,势力值系数μ=0.2。NSGA-II中交叉概率为0.7,变异概率为0.02。MOSA中初始温度值为1 000,冷却系数0.98。
3.1.2 结果分析
首先,针对所有数据集进行MOICA、NSGA-II和MOSA的仿真验证,同时利用多目标优化解的评价指标进行对比,具体如表3所示。由于元启发式算法(如模拟退火、遗传算法、帝国竞争算法)的优化结果与参数以及初始化息息相关,表3的结果基于20次独立仿真的均值进行对比。
由表3可知:对于14组仿真数据集,覆盖率指标(CCM),MOICA全面优于NSGA-II与MOSA;空间分布指标(CSP),MOICA最优,MOSA较劣;超体积指标(CHV),MOICA在12组数据集中占优;平均理想距离(CMID),MOICA在13组数据集中占优。通过计算各组数据在各类指标下的均值可见,MOICA的帕累托最优解相对于NSGA-II与MOSA而言,解集更占支配地位(CCM)、解集的分布更均匀(CSP)、解集的收敛性更好(CHV)、解集的质量更高(CMID)。进一步分析MOICA解集非占优的情况发生在小规模数据集OR#13.1/OR#13.4/OR#13.7,原因在于上述数据集的压缩因子Kd较大,对应进场需求低,排序与调度难度较小。此时,NSGA-II与MOSA也能获得较优解。对于最复杂数据集OR#13.6,本文提出的MOICA表现更好。
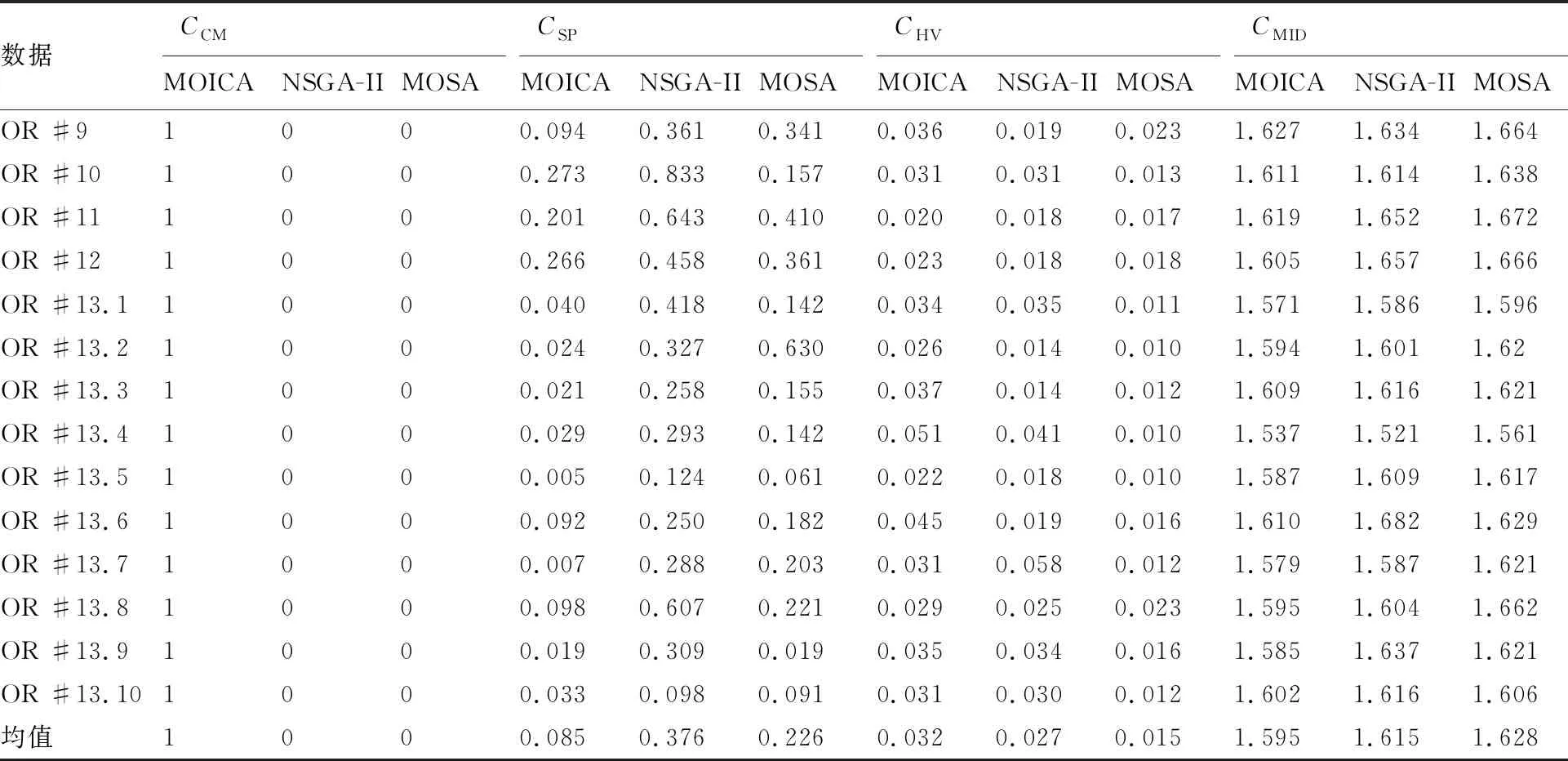
表3 OR数据集仿真结果对比
其次,选取数据组OR #9,应用MOICA、NSGA-II与MOSA分别进行500次独立实验。针对仿真结果计算指标:空间分布、超体积、平均理想距离,并将500组评价指标以四分位图的方式显示仿真结果,如图3所示。

图3 多目标优化解评价指标的四分位图
由图3可知:OR #9数据的500次独立实验结果进一步验证了相对于NSGA-II与MOSA而言,MOICA的优越性。覆盖率指标未列入,原因在于MOICA帕累托解集均占支配地位。
最后,为了考察多目标优化算法的运算效率,图4提供了不同数据集的CPU时间示意图,无论是本文提出的MOICA,还是对比的NSGA-II,小规模数据集的迭代次数设为150次,大规模数据集的迭代次数设为250次。
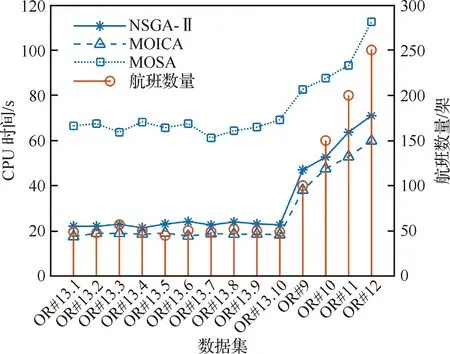
图4 多目标优化运行时间对比
由图4可知:一方面,本文提出的MOICA其算法效率均优于NSGA-II与MOSA;另一方面,多目标优化算法的运行效率主要依赖于迭代次数和航空器架次,当迭代次数一致时(如大规模数据集,imax=250),数据集规模越大其优化时间越长。
3.2 实际数据优化分析
3.2.1 仿真场景构建
以长沙黄花机场(四字码ZGHA))进场运行为例,图5显示了2019年12月26日8:00—2019年12月27日8:00共计233条进场航空器的综合航迹,长沙机场共有5个进港点(BEMTA, LLC, LIG, OVTAN, DAPRO)。
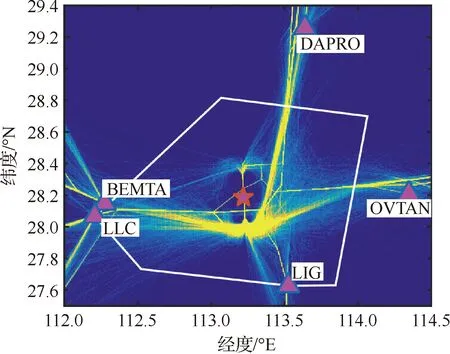
图5 长沙黄花机场进场运行航迹示意图
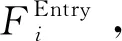
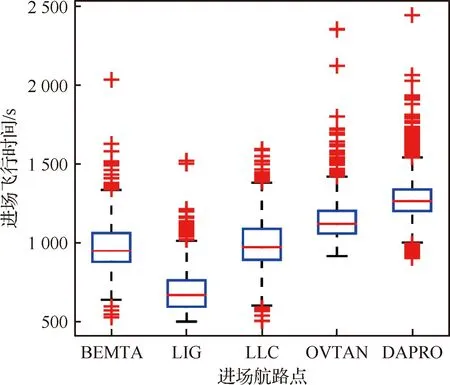
图6 进场航空器飞行时间四分位图
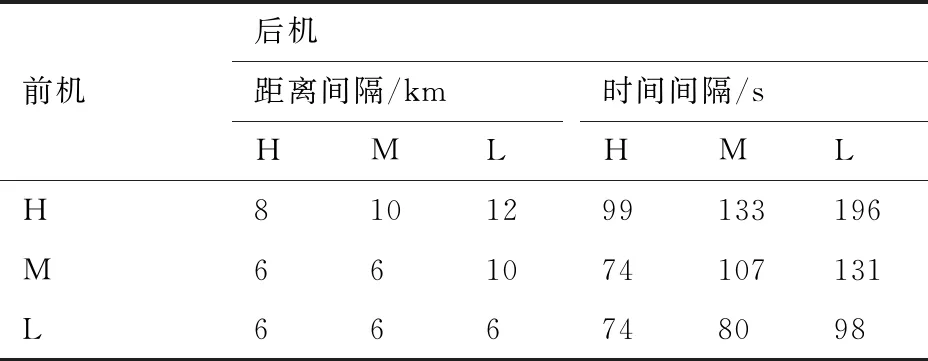
表4 尾流间隔标准[22]
3.2.2 仿真结果分析
利用本文提出的MOICA实现长沙机场的进场排序与调度优化,选取23:00—00:30内的21架进场航空器作为优化对象,相关参数的设定同3.1节的大规模数据集。
在本次的实例仿真中,尾流间隔分别选取表4 对应标准的1.2倍、1.5倍和1.8倍实施验证,其总延误时间,总飞行时间和最大飞行时间的优化结果如表5所示。
由表5可知,利用MOICA实现进场的排序与调度可以有效地提升运行效率与效益,兼顾空管、航司、机场、民众的不同诉求。即便是将尾流间隔限制扩大到现行标准的1.8倍,相对于管制实际运行结果,总延误时间可以降低41.2%、总飞行时间可以减少11.4%、最大飞行时间可以缩短8.6%。

表5 实际案例仿真验证结果
进一步,为考察实际着陆序列与优化着陆序列的变化情况,图7以时序图的形式,展示了1.5倍标准间隔设置下,各进场航空器在不同进港点(Entry-FIX)的出现时间(黑色圆圈所示)与序列、各进场航空器的预计着陆时间(Estimate Time of Arrival, ETA)(绿色三角所示)与序列、各进场航空器的优化着陆时间(Schedule Time of Arrival, STA)(蓝色菱形所示)与序列、各进场航空器的实际着陆时间(Actual Time of Arrival, ATA)(红色方框所示)与序列。
由图7可知,1.5倍的间隔标准与实际管制运行时的安全间隔相仿,引入MOICA的优势在于通过调整着陆次序,最大可能地逼近设置的尾流安全间隔,从而实现总延误时间、总飞行时间以及最大飞行时间地减少。至于管制员在实际运行中未能应用最佳着陆序列的原因,可以通过不同时间点进场航空器态势加以解释,如图8所示。
图8展示了从23:30—23:55这段时间内,10架进场航空器的运行态势。航空器的选择是基于图7的分析。
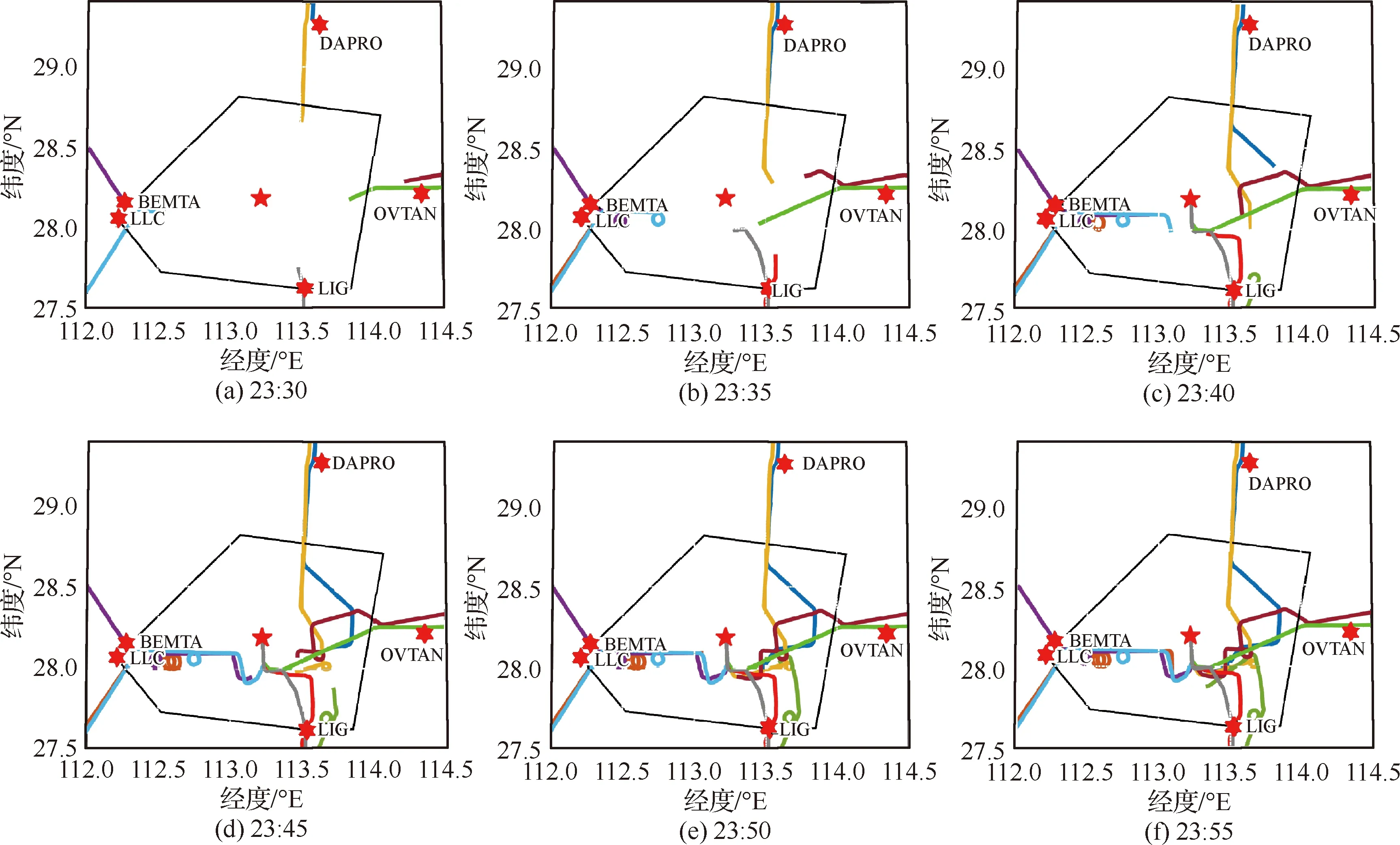
图8 进场航空器不同时刻的态势示意图
由图7可知,进场航空器可以粗略分为3个“波次”,第1波共有12架;第2波共有4架;第3波也是4架。前12架中,可以忽略第一架与最后一架着陆的航空器(均由DAPRO进港),因此余下10架的构成为:2架次DAPRO进港,1架次BEMTA进港,2架次LLC进港,3架次LIG进港,以及2架次OVT进港。管制员对于西向进港(LLC/BEMTA)航空器的调配策略是等待;对于北向(DAPRO)和南向(LIG)进港航空器使用向东侧偏离策略;至于东向进港(OVTAN)航空器则向北侧调配。23:35和23:40时,管制员发现着陆需求较为旺盛,于是分别按既定策略引导进场航空器作机动飞行。此时,管制员引导主要依赖经验,兼之飞行员具体操控航空器时对管制员指令的依从度无法预知,最终导致无法充分利用终端空域以及跑道的容量。因此,MOICA可以为管制员提供着陆序列与时间的决策支持,至于如何给定确切的管制指令,本文拟借助于点融合系统 (Point Merge System, PMS) 实现。
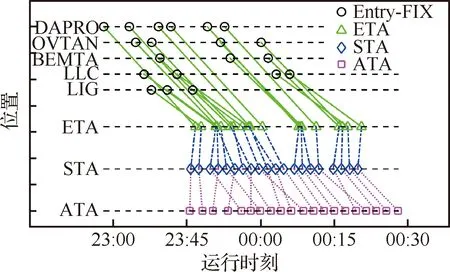
图7 进场航空器着陆时序对比示意图
基于统计分析获取飞行时间或者采用四维航迹预测[24],能够实现进场运行“可见”目标;采用本文提出的MOICA兼顾各利益相关方的诉求开展排序与调度,可以实现进场运行“可优”目标;如何基于优化的着陆序列与时间向管制员提供决策支持,方能实现进场运行“可达”目标。为此,本文拟通过PMS解决优化结果“可达”的问题。图9提供了引入PMS后的进场程序,以及基于该程序和1.2倍间隔标准优化结果的进场航空器运行示意图(注:1.5倍间隔标准的配备需要通过引入标准等待实现)。
由图9可见,PMS的引入具备如下优势:①进 场排序与调度优化结果的可达,根据优化着陆序列与时间反推PMS程序结构下的航空器四维轨迹,为管制员提供决策建议;② 管制决策建议简单有效,将传统的管制指令简化为排序支路上的转弯,降低了管制工作负荷;③ 由于管制引导仅发生在排序支路上,提升了飞行员的态势感知与情境意识;④ 飞行轨迹更为规整有序,有效降低了终端空域进场运行的复杂性。值得注意的是,由于引入PMS导致预计到达时间与着陆时间窗变化,因此表5的相关结论需要另行计算。
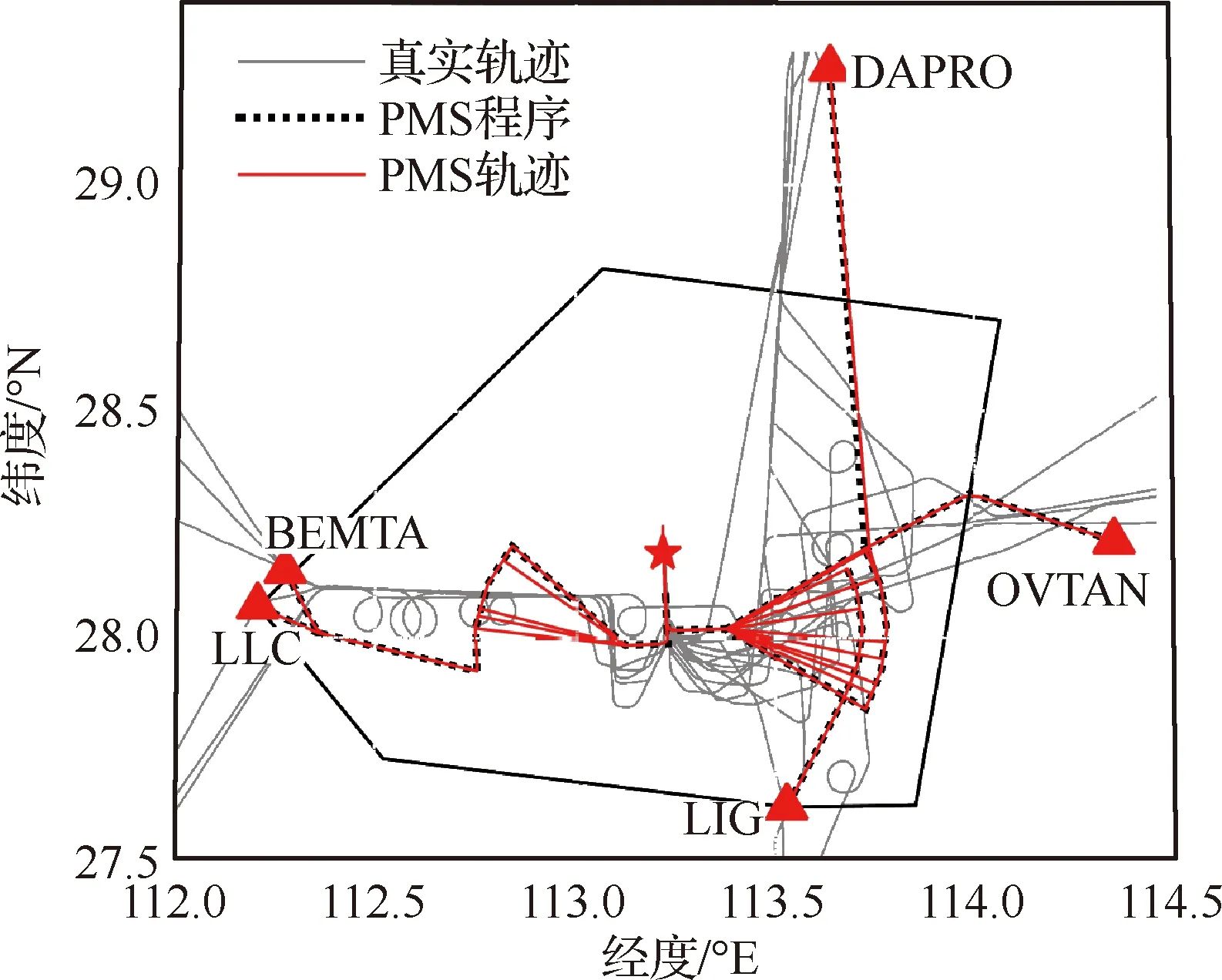
图9 引入PMS的进场排序与调度运行示意图
4 结 论
1) 借鉴机器调度领域的研究成果,梳理和删减进场排序与调度问题所对应的目标函数,最终确定3个指标:最小化总延误时间、最小化总飞行时间、最小化最大飞行时间。从理论角度分析和证明,上述目标能够同时满足空管、航司、机场以及民众的不同诉求。
2) 面向3个目标,考虑着陆时间窗约束、尾流间隔约束、航空器着陆次序的最大位置转换约束等,构建进场排序与调度多目标优化模型,以实现管制工作负荷降低、跑道运行容量增强、航空器正点率提升、各航司调度公平的目的。
3) 基于非支配排序,设计了多目标帝国竞争算法,求解多目标进场排序与调度模型的帕累托解。同时,引入覆盖率指标、空间分布指标、超体积指标和平均理想距离等指标,衡量帕累托解集优劣。
4) 从两个角度实施仿真验证:一方面,利用基准案例(OR数据集)对比多目标帝国竞争算法(MOICA)与多目标遗传算法(NSGA-II)及多目标模拟退火算法(MOSA)的解集质量与求解效率;另一方面,利用实际运行案例考察本文提出方法的有效性,并引入点融合系统保障优化结果的可行性。
5) 本文主要解决了单跑道进场排序与调度问题,未来的研究会扩展到多跑道、进离场、以及多机场终端空域的运行场景。
