考虑电池电-热-放电深度的并联PHEV能量管理策略研究*

解少博，张康康，张乾坤，罗慧冉

（长安大学汽车学院，西安 710064）

前言

插电式混合动力汽车（PHEV）具有节能、减排和克服里程焦虑等特点，还可与电网的“互动”并构成能源网络，展现出巨大的市场潜力。配置有自动机械式变速器（AMT）的并联PHEV还可改善车辆的动力性和经济性，并有效减轻驾驶人的工作负担，在城市公交领域备受青睐［1］。

PHEV包含发动机和电机等多个功率源，为优化系统效率、提升整车经济性，需要设计合理的能量管理策略（EMS）。典型的EMS包括规则型策略、基于全局优化方法如动态规划［2］和庞特里亚金最小值原理［3］以及等效能耗最小化策略［4］等。近年来在工业控制领域越来越受到关注的模型预测控制（MPC）［5］，能在滚动时域内实时优化，既具有实时性且能够实现局部优化，展现出独特的优势。

动力电池成本在整车总成本中占有很高比重。在EMS的开发中充分考虑电池的老化因素以延长其使用寿命，对整车经济性和全生命周期价值的提升意义重大［6］。然而，电池老化受多种因素的影响，例如充放电倍率、环境温度和放电深度等，并且这些因素相互耦合［7］。

研究人员针对考虑电池寿命的EMS已展开了广泛研究。针对HEV，文献［8］中应用PMP使电池健康状态（SOH）保持在合理范围内。文献［9］中通过在目标函数中施加惩罚项来抑制电池温度，优化功率分配关系。文献［10］中针对配备有AMT的纯电动客车，构建了考虑电池老化效应的换挡策略。文献［11］中针对配置有AMT混合动力汽车的能量管理，考虑了充放电和温度等影响电池老化的因素。

对于含AMT的并联式PHEV，为提升经济性，应同时优化挡位选择和转矩分配。一方面，挡位选择和转矩分配是相互影响的，在EMS的设计中需要同时对两者进行优化，即形成二维优化问题。另一方面，对挡位进行优化可以提供额外自由度来选择更合理的功率分配关系，从而有助于抑制电池的充放电电流并减小电池的老化成本。现有针对PHEV考虑电池老化的EMS未能全面考虑影响电池老化的因素，尤其是放电深度。针对并联PHEV的EMS也未能探讨挡位优化对电池老化的抑制作用。

基于上述考虑，本文中针对在固定路线上运行的配置AMT的插电式混合动力公交客车，考虑电池电-热-放电深度等多重耦合因素，确定整个行程的最佳放电深度，同时考虑换挡和转矩分配两个优化变量并构建具有实时性的能量管理策略，从而实现换挡、转矩分配和电池寿命等多重目标的协同优化。

1 并联PHEV动力系统

1.1 动力系统结构

并联PHEV动力系统结构如图1所示。发动机与电机既能单独驱动车辆，也可以将动力耦合实现联合驱动。整车和动力部件的参数如表1所示。

图1 PHEV动力系统结构

表1 整车和动力部件参数

1.2 动力系统模型

柴油发动机的燃料消耗率特性如图2所示，发动机燃油消耗率可表达为转速和转矩的函数［1］。

图2 发动机燃油消耗特性图

电机效率图如图3所示，其效率可表达为转速和转矩的函数。

图3 电机效率特性图

2 电池模型

2.1 电池电路模型

电池由168个单体串联成组，额定容量为100 A·h，总电压为537.6 V。假设电池电路参数不随温度变化，每个电池的开路电压和等效内阻表示为SOC的函数，如图4所示。

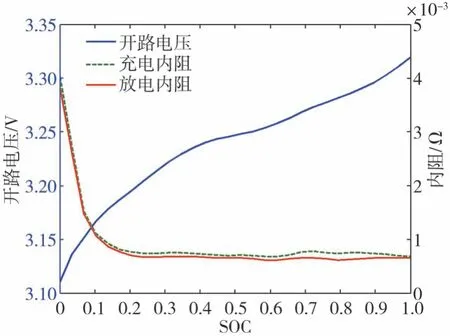
图4 电池单体开路电压和内阻随荷电状态（SOC）的变化

单体电池的电压方程和SOC动力学方程分别为

式中:UL和Uoc分别为端电压和开路电压；Ib为电流；Rin为等效内阻；Qb为电池容量。

2.2 电池热模型

本文中基于圆柱形磷酸铁锂电池（A123 ANR26650M1）的热模型来描述电池的传热动力学，其动力学公式［12］可表达为

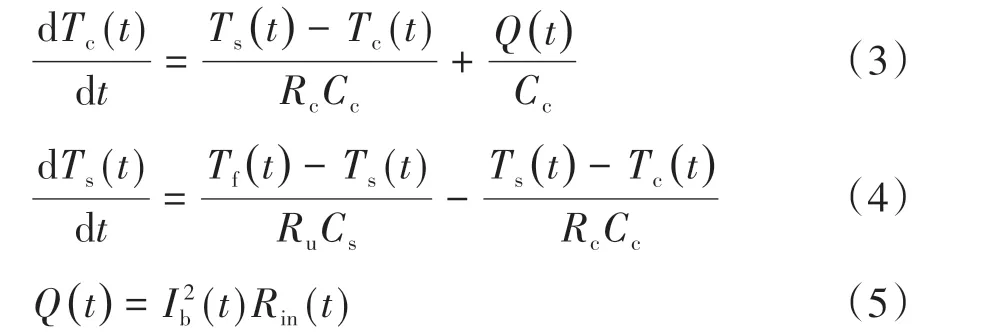
式中:Tc和Ts分别为圆柱形电池的核心温度和表面温度；Tf为电池单体所在环境的温度；Q为焦耳热；Rc和Ru分别为导热电阻和对流电阻；Cc和Cs分别为电芯热容量和表面热容量。

考虑到电池单体与周围介质的换热过程十分复杂，其精确的物理模型很难建立。为此，假设电池单体周围环境温度随车速而变化，可近似表达为［11］

式中:v为车速；Qt为单个电池模块生成的总热量；Qr为电池包向周围介质如空气等散发的热量；Ce为周围介质的等效比热容；mb为周围介质的质量；Aep和Kep分别为等效传热面积和传热系数；Ten为电池包所在环境的温度。当车辆静止时，CT取负常数。

2.3 电池老化模型

若定义20%容量损失表示电池寿命的结束，则标称安时吞吐量Γnom可表示为［10］

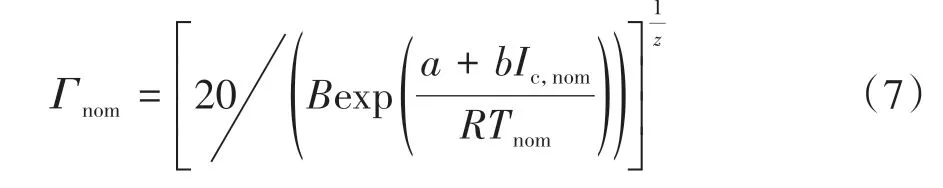
式中:B为指数前因子；Ic，nom和Tnom分别是标称的电池放电速率和核心温度；R为气体常数，J·mol-1·K-1；a和b为拟合系数；z为指数因子。

为量化相对于标称安时吞吐量的电池老化［14］，定义衰减因子σ为

式中Γ为实际工作条件下的安时吞吐量。

3 能量管理策略

3.1 能量管理策略架构

提出的能量管理策略架构如图5所示。首先，对于在固定路线上运行的插电式混合动力客车，根据车速谱并基于电池老化动力学（考虑影响电池寿命的电-热-放电深度等耦合因素）确定最佳放电深度。其次，基于获得的最佳放电深度和短时车速预测对滚动时域内的电池进行放电规划，即SOC规划，从而为模型预测控制提供滚动时域内的SOC边界约束。最后，应用优化算法（PMP）实现滚动时域内挡位选择和转矩分配的协同优化。

图5 考虑电-热-放电深度的并联PHEV能量管理策略架构图

3.2 目标函数

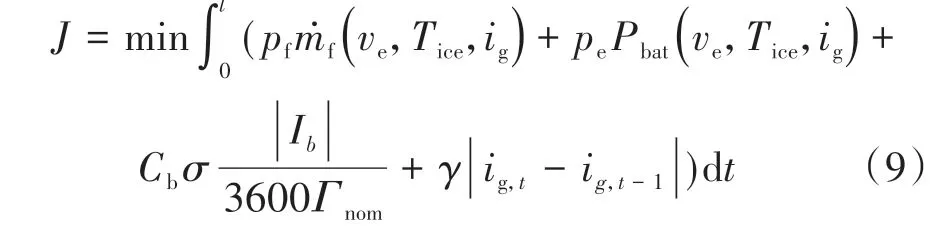
考虑能耗成本、电池老化成本和对频繁换挡的抑制，以滚动时域内三者之和最小化为目标定义目标函数:式中:l为滚动时域长度；pf和pe分别为燃料和电能价格；ṁf为发动机燃油消耗率；Pbat为电池功率；Cb为电池购买成本；γ|ig，t-ig，t-1|为抑制频繁换挡的惩罚项；γ为预设因子；ig为挡位传动比；t为时刻。

4 电池最优放电深度

对电池在整个行程上的最优放电深度进行辨识，从而为滚动时域内的SOC规划提供边界条件。从西安市某固定公交线路（线路总长约为71 km）上采样的真实速度曲线用于计算最佳放电深度，在此选择了5个速度谱（No.1⁃No.5），如图6所示。

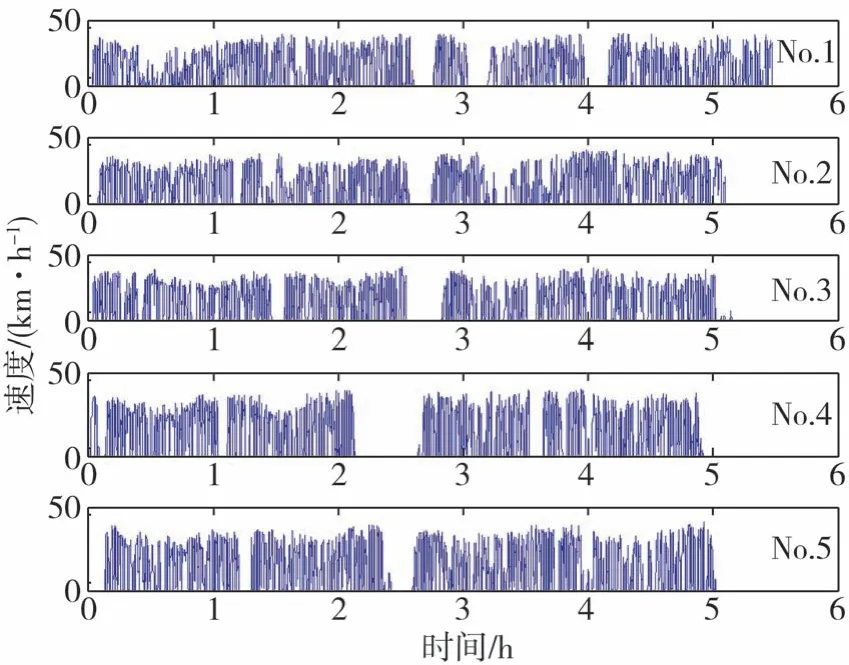
图6 公交线路车速谱

初始SOC设为0.9，气体常数R为8.31 J·mol-1·K-1，环境温度Tf设为298.15 K，系数α和β分别为-31 700和370.3，预指数B为31 630，指数z为0.55。柴油和电能的单价分别设为5.72和0.8 CNY·（kW·h）-1，电池的单位购置成本设为1 900 CNY·（kW·h）-1，导热电阻Rc和对流电阻Ru分别为1.94和3.08 K·W-1，电芯热容量Cc和表面热容量Cs分别设为62.7和4.5 J·K-1，另 设 周 围 介 质 的 等 效 比 热 容Ce为810.0 J·（kg·K）-1，周围介质质量mb为3.1 kg，常数CT设为-3.5×10-4K/s。

以No.1车速谱为例说明最优放电深度（ODOD）的确定过程。在PMP的数值求解过程中，使用自由边界打靶方法得到总成本相对于放电深度（DOD）的变化曲线，如图7所示，其中考虑到了电池温度的变化。可以看到，总成本和DOD近似呈现抛物线关系，原因是能量消耗成本（燃料消耗成本和电能消耗成本之和）和电池老化成本是负相关的，即随着电池使用量的增加，能耗成本将减少，而电池老化成本将增加。

图7 总费用随电池放电深度的变化曲线

表2给出了4个车速谱的计算结果，包括燃料消耗量（FC）、电能消耗量（EC）、电池老化成本（BAC）、总费用、电池温度变化（ΔT）和ODOD。由于每天交通状况不同以及天气、出行量等随机因素的影响，车速谱会有不同，导致每个ODOD略有差异。这里取ODOD平均值表示最优放电深度。

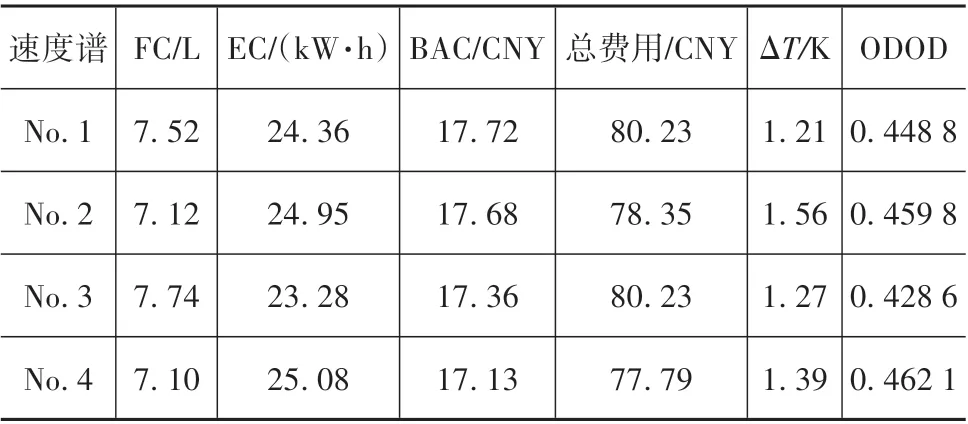
表2 不同速度谱的结果

5 短时车速预测

在滚动时域内对SOC进行规划需要对车速进行预测。使用包含输入层、中间层和输出层的3层BP神经网络用于速度预测［7］，其结构如图8所示。输入层为历史的短时速度序列，输出为未来短时速度序列。

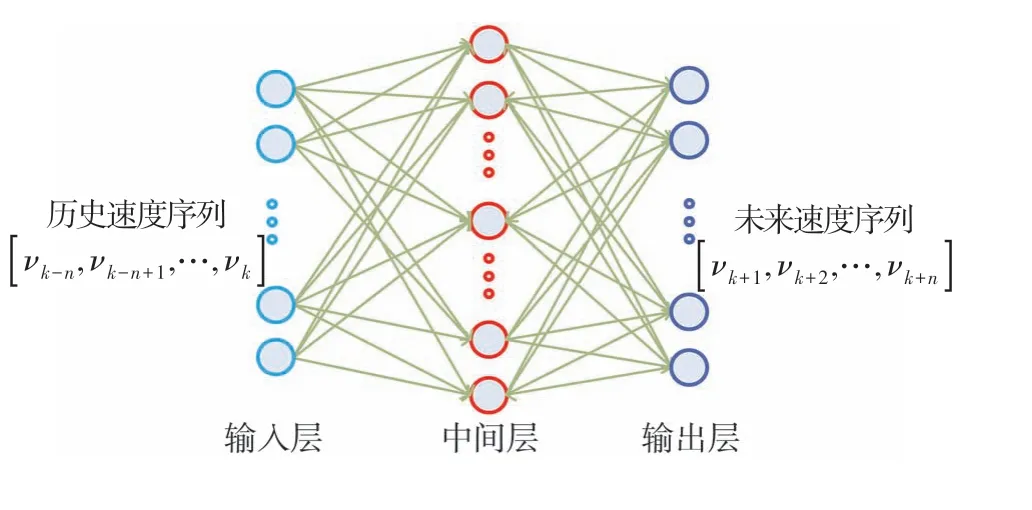
图8 用于速度预测的3层神经网络

以前述4个速度谱（No.1-No.4）为样本进行神经网络的训练，以No.5速度谱进行预测结果的验证。随着预测时域的增大，历史速度序列与未来速度序列之间的关联逐渐变弱，即预测误差随着预测时域的增大而增大，定量的结果表明在3个预测时域下（5、10和15 s）的速度预测均方根误差分别为2.21、5.10和7.09 km·h-1。

6 结果与分析

对于并联PHEV的模型预测控制，首先使用BP神经网络对滚动时域内的车速进行预测，其次在滚动时域内执行PMP优化算法［15］，最后将所得控制序列的第1个元素施加于被控对象，即将预测时域内解的序列的第1个元素（转矩分配关系和挡位选择）提取出来作为车辆动力系统的输入。此外，在求解滚动时域内的优化问题时，应满足SOC的边界约束。本文通过SOC规划得到预测时域内的SOC约束［15］。

以No.5车速谱为例对提出的能量管理策略进行评估。电池初始SOC设为0.9，根据最佳放电深度取SOC下限为0.449 8。同时，对比了3种不同预测时域（5、10和15 s）对MPC性能的影响。

6.1 二维MPC

表3为2D⁃MPC⁃w的结算结果（后缀-w表示考虑电池老化的MPC）。可以看到，3种预测时域的燃料和电耗成本以及电池老化成本均相近，从而总成本也较为接近。预测时域虽然增加，但总成本几乎保持不变，这可以解释为:尽管较长的预测时域可以扩大滚动时域的优化尺度，这有利于降低总成本，但同时会降低速度预测的准确性，进而在两方面综合效果下总成本保持不变。而计算时间随预测时域的增加快速增长。3种情况下电池电芯温度大约增加了1.6 K。

表3 2D⁃MPC⁃w的结果

进一步分析可知，预测时域为5 s时的总成本与其他情况接近，但时间效率更高。综合经济性和计算效率两个方面，选择5 s作为最终的预测时域。发动机和电动机的工作点分别如图9和图10所示。由图可知，发动机的工作点大多集中在最佳燃油消耗率区域，电动机既有电动模式又有发电模式，且大多数工作点都处于高效率区。

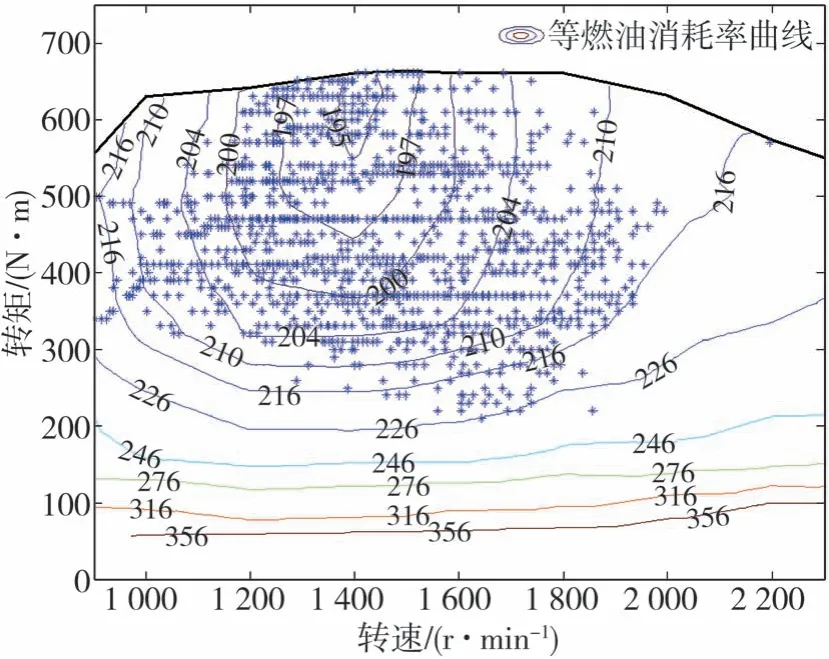
图9 预测时域为5 s时的发动机工作点

图10 预测时域为5 s时的电机工作点

6.2 一维MPC

为与2D⁃MPC⁃w进行比较，基于规则换挡策略的一维MPC（1D⁃MPC⁃w）仅对发动机和电机之间的输出转矩分配进行优化，而换挡策略基于预先设定的规则来实施［1］，其中选择变速器输出轴转矩和转速为换挡的两个参数。

表4为定量计算结果。与2D⁃MPC⁃w相似，1D⁃MPC⁃w产生的能耗、电池老化成本以及电池核心温度变化在3种预测时域下相近，从而总成本也几乎接近。但与2D⁃MPC⁃w的温度上升约1.6 K相比，1D⁃MPC⁃w的电池核心温度上升了约2 K，导致对应的BAC高于2D⁃MPC⁃w。此外，由于规则型换挡策略无法保证发动机和电机始终运行在高效工作区，从而削弱了燃油经济性，因此1D⁃MPC⁃w的总成本比2D⁃MPC⁃w高约1.5 CNY。

表4 1D⁃MPC⁃w的结果

发动机和电机的工作点如图11和图12所示。对比可知，1D⁃MPC⁃w的工作点覆盖的高效区在整体上不如2D⁃MPC⁃w显著。在计算时间方面，1D⁃MPC⁃w所需的时间比2D⁃MPC⁃w有所减少，因为前者无须搜索最佳挡位，从而可以减少对应的计算消耗。

图11 1D⁃MPC⁃w发动机工作点（预测时域为5 s）

图12 1D⁃MPC⁃w电机工作点（预测时域为5 s）

6.3 不同方法比较

进一步将2D⁃MPC⁃w与其他方法进行了比较，包括2D⁃MPC⁃w/o（后缀-w/o表示不考虑电池老化的MPC），1D⁃MPC⁃w，1D⁃MPC⁃w/o，基于DP和PMP的全局优化算法，以及基于规则的CD⁃CS策略，结果见表5。可以看出，电池老化成本在总成本中起着至关重要的作用。以CD⁃CS为例，如果忽略BAC，则能量消耗成本为81.1 CNY，而包括电池老化模型，总成本实际上增加到117.0 CNY，BAC占总成本的30.7%。

对于能耗经济性，PMP⁃w/o和DP⁃w/o作为全局方法形成的总成本最低，而CD⁃CS作为基于规则的策略形成的总成本最高。CD⁃CS策略使电池核心温度上升达6.92 K，这也导致了最高的BAC。PMP⁃w/o和DP⁃w/o策略的总成本十分接近，主要原因是两者都从全局角度考虑能量分配。与CD⁃CS相比，DP⁃w/o和PMP⁃w/o可以使总成本分别降低30.7%和30.7%。

从表5还可以看出，与不考虑电池老化模型的策略相比，考虑老化的策略可以通过调节电池输出功率来降低电池温度，并进一步降低总成本。特别地，与2D⁃MPC⁃w/o相比，2D⁃MPC⁃w可以将总成本从84.63减少至84.06 CNY。

通过将挡位作为另一个优化变量，2D⁃MPC⁃w和2D⁃MPC⁃w/o的总成本分别比1D⁃MPC⁃w和1D⁃MPC⁃w/o降低1.77%和1.05%。与CD⁃CS策略相比，2D⁃MPC⁃w可使总成本降低32.93 CNY，即总成本降低28.2%。同时作为实时预测方法的2D⁃MPC⁃w与全局优化方法PMP⁃w相比，总成本提高了约4.13%，这是因为2D⁃MPC在本质上属于局部优化。

在计算效率方面，2D⁃MPC比1D⁃MPC的计算时间增加约10%，因为2D⁃MPC增加了寻找最佳挡位的计算时间。同时可见，CD⁃CS策略最省时，但总成本最高。

不同方法的SOC曲线如图13所示。其中，CD⁃CS策略首先是电荷消耗阶段，然后是电荷维持阶段，而其他方法的SOC曲线在整个行程中大致呈线性下降。当车辆保持静止时，可以在2.3-2.7 h观察到SOC的平台阶段。

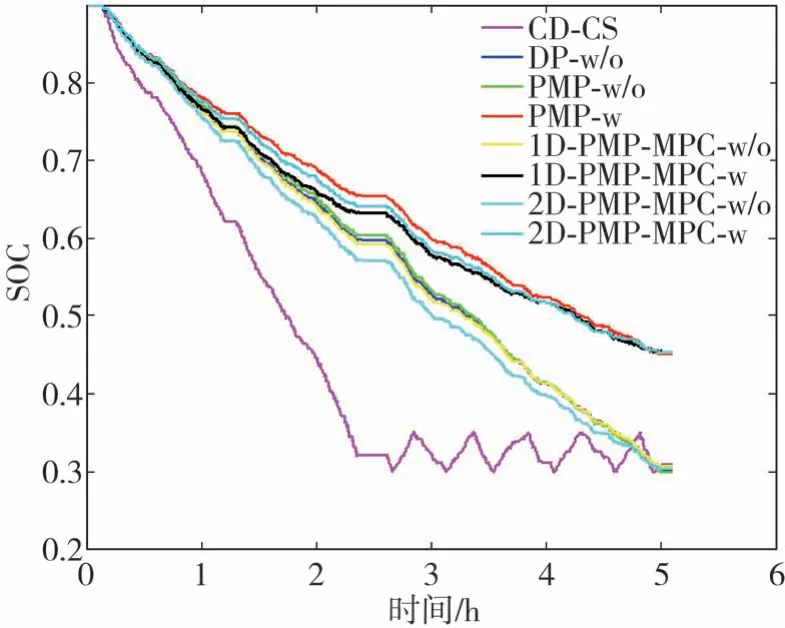
图13 SOC轨迹曲线

图14为不同方法下电池核心温度的变化曲线。总体来看，行程结束后，所有策略的电池温度都会升高，但在行驶过程中也会出现电池核心温度下降的情况，主要因为行驶中出现了停车的情况，在该情况下基于本文电池热模型，其核心温度会通过与外界的换热而下降。对于CD⁃CS方法，整个行程电池温度升高了6.92 K，与其他方法相比，核心温度增长较为显著。这是因为CD⁃CS以规则的形式使用电池，放电电流相对较大，导致核心温度上升明显。对于不考虑电池老化（DP⁃w/o和PMP⁃w/o）的全局方法，两者产生了相似的核心温度上升曲线，最终温度分别上升了2.63和2.66 K。考虑了电池老化模型（PMP⁃w）的全局方法的电池核心温度升高最慢，温度上升1.48 K，因为PMP⁃w在考虑到电池寿命的同时优化了挡位选择和转矩分配。

图14 电池核心温度随时间的增长曲线

与2D⁃MPC⁃w/o相比，2D⁃MPC⁃w形成了缓慢的电池核心温度增长速率。与前者相比，后者温升幅度降低39.3%。在1D⁃MPC⁃w/o和1D⁃MPC⁃w中也发生了类似的现象。这可以解释为:MPC⁃w（2D⁃MPCw和1D⁃MPC⁃w）的目标函数考虑了BAC，与MPC⁃w/o（2D⁃MPC⁃w/o和1D⁃MPC⁃w/o）相比，其能量分配策略有利于抑制放电电流，这也可以从图15的电池输出电流的情况得以反映。可以看出，2D⁃MPC⁃w中流入和流出电池的电流小于1D⁃MPC⁃w，而电池电流与BAC和核心温度上升成正相关关系。这表明前者在降低电池芯温度方面更有优势，因为通过优化挡位选择和转矩分配，2D⁃MPC⁃w能够为抑制电池放电电流提供更多自由度。

图15 1D⁃MPC⁃w和2D⁃MPC的电池输出电流

7 结论

针对含AMT的PHEV，提出考虑电池电-热-放电深度耦合的能量管理策略，对挡位选择和转矩分配同时优化，形成二维优化控制问题。主要结论如下。

（1）考虑电池老化的1D⁃MPC⁃w和2D⁃MPC⁃w分别与不考虑电池老化的1D⁃MPC⁃w/o和2D⁃MPC⁃w/o相比，能够降低电池老化成本及核心温度。此外，与基于规则换挡策略相比，2D⁃MPC有利于降低电池老化成本和电池核心温度，因为换挡选择提供了额外的自由度来限制电池放电电流，有利于温升的抑制。

（2）对于71公里的城市公交路线，所提出的方法（2D⁃MPC⁃w）与基于规则的CD⁃CS策略相比，可以降低总成本（能耗成本和电池寿命损失成本之和）28.2%。此外，与1D⁃MPC⁃w相比，2D⁃MPC⁃w可以降低总成本1.52 CNY。

（3）相比于一维MPC，二维MPC由于将挡位作为另一个优化变量，使其计算时间约增加10%。

换挡策略不仅影响到经济性，还关系到整车的平顺性，在将来的工作中将对这一方面深入研究。