基于数据驱动的双离合器自动变速器换挡过程自适应控制*

2021-07-05刘永刚张静晨万有刚孙冬野秦大同

汽车工程 2021年6期

刘永刚，张静晨，万有刚，孙冬野，秦大同

（1.重庆大学，机械传动国家重点实验室，重庆 400044；2.重庆大学机械与运载工程学院，重庆 400044）

前言

近年来双离合器自动变速器在汽车领域受到广泛关注，一些汽车厂商在燃油车、插电式混合动力汽车上大量应用DCT作为变速器。DCT的换挡通过滑摩控制使动力在两个离合器之间切换来实现，而换挡过程的动力响应速度和产生的冲击较大地影响了驾驶员的主观感受。为解决这一问题，众多学者对换挡过程控制器的设计开展了大量研究。

在基于模型的DCT换挡控制方面，Liu等［1］设计了PID控制器和模糊控制器，对离合器主、从动盘转速进行跟踪控制。赵治国等［2-4］设计了高阶滑模观测器进行离合器转矩估计。Oh等［5-7］设计了自适应滑模控制器进行离合器转矩跟踪控制。Walker等［8-10］设计了联合扩展卡尔曼滤波器和双扩展卡尔曼滤波器进行离合器转矩估计。上述控制器可实现转速或转矩的闭环跟踪控制，但是在DCT系统性态参数随服役时间发生变化或存在内外部干扰时，DCT的换挡品质难以保证。因此，众多学者对DCT换挡鲁棒性控制做了相关研究。

在DCT换挡鲁棒性控制方面，Song等［11］通过对湿式离合器液压系统精确建模，设计了基于非线性状态观测器的换挡过程滑模控制器，结果表明该控制器具有较好抗干扰能力。Hu等［12］通过反步法设计了DCT换挡过程非线性控制器，提高了控制系统鲁棒性。Wu等［13］基于哈密尔顿-雅可比不等式设计了滑模控制器，结果表明该控制器对离合器摩擦因数的变化和外部扰动具有较高的鲁棒性。Kim等［14］设计了自适应鲁棒控制器，解决了存在内外部干扰时的鲁棒控制问题。上述控制器都依赖于复杂的高阶非线性动力学模型，但对于系统性态参数随服役时间的变化规律和内外部干扰下难以准确建模。这也是所有基于模型的控制方法都存在的共性问题，即使通过一些鲁棒性设计可提高控制器性能，但仍存在较大的提升空间。因此，本文中提出一种基于数据驱动的DCT换挡过程自适应控制方法。

以某厂家提供的7速湿式双离合器自动变速器为研究对象，首先开展实车实验获取换挡品质较好的换挡数据，作为控制器的参考转速和转矩；基于无模型自适应控制算法，设计基于数据驱动的DCT换挡过程自适应控制器；建立DCT系统换挡过程仿真模型，对存在内外部干扰和系统性态发生变化的情况进行仿真，验证控制器的控制效果、鲁棒性及自适应能力。

1 数据预处理

以行驶记录仪和AVL客观评价系统为核心建立了DCT车辆的集成数据采集系统，在不同条件下进行多次换挡过程实验，获得换挡过程数据。由于车辆传感器存在噪声，测得的数据无法直接使用，因此需要对所得数据进行去噪处理。同时，统计出每一次换挡的冲击度、滑摩功和持续时间，并筛选出换挡品质较好的数据，在仿真验证时可作为控制器的参考值。

首先，基于小波阈值法对传感器测得的数据进行去噪。小波阈值去噪能够完成信号时域和频域上的变换，提取出可以使用的真实换挡数据。去噪阈值函数是影响小波阈值去噪的重要因素，常用的硬阈值函数会产生附加振荡，软阈值函数误差较大，都存在难以接受的缺陷，因此，结合硬阈值函数和软阈值函数的特性，选用综合性能较好的半软阈值函数进行去噪。半软阈值函数的数学表达式为

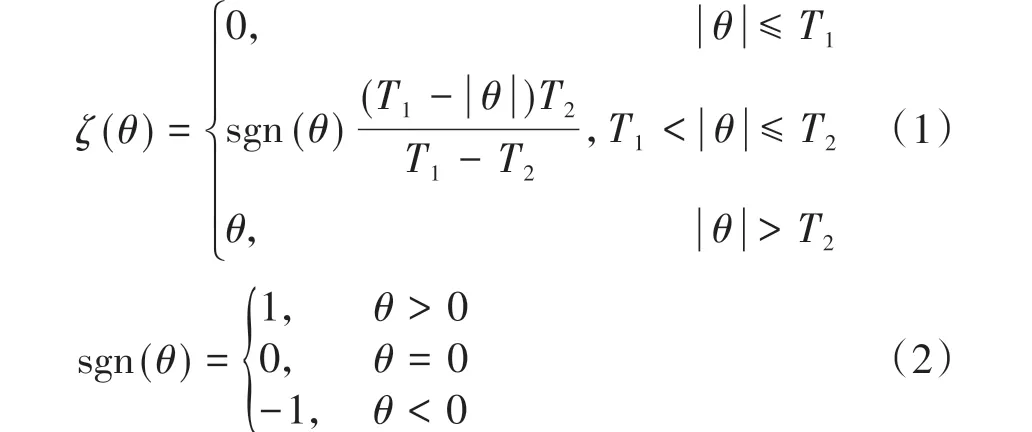
式中:θ为信号的高频部分；T1、T2为常数。

以节气门开度信号为例，小波半软阈值去噪结果如图1所示。

图1 节气门信号及其小波半软阈值去噪结果

在完成数据去噪后，对每一次换挡的品质进行评价，评价指标分别为换挡冲击、滑摩功和换挡持续时间［15］，其中换挡冲击和滑摩功的计算公式如下:

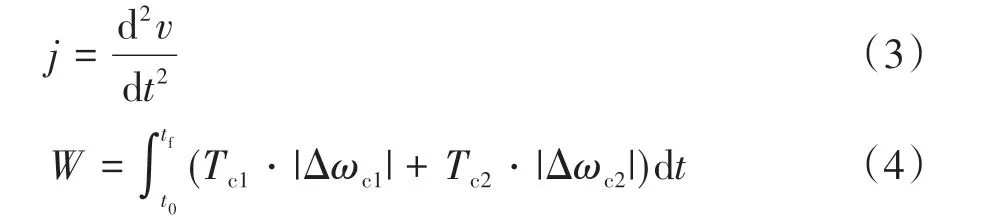
式中:v为纵向车速，m/s；Tc1和Tc2分别为离合器1和离合器2的滑摩转矩，N·m；Δωc1和Δωc2分别为离合器1和离合器2的主、从动盘角速度差，rad/s。

根据上述评价指标，从实验获得的大量换挡数据中，统计出不同油门开度下换挡品质相对较好的换挡曲线。其中，将离合器主、从动盘转速作为控制器的参考转速，将离合器滑摩转矩作为控制器的未补偿初始控制量。

2 DCT换挡过程数据驱动控制器设计

2.1 控制方案

为保证DCT系统在换挡过程中能够准确跟随实验提取的参考转速曲线，并在没有精确动力学模型的条件下完成自适应控制，采用无模型自适应控制（model⁃free adaptive control，MFAC）方法设计基于数据驱动的DCT换挡控制器。

MFAC控制器根据非线性系统的输入输出数据实时构建动态数据模型，实现闭环跟踪控制，并具有鲁棒性强、计算量小的优点［16］。其结构如图2所示。

图2 MFAC控制器结构图

具体控制方案如图3所示，根据实时测得的真实离合器转速与实验获取的离合器参考转速，通过MFAC控制器计算得到离合器补偿转矩，再将补偿转矩与离合器参考转矩加权融合得到系统控制量，实现闭环转速跟踪控制。

图3 换挡过程控制方案

MFAC控制器的核心为控制率的推导和伪偏导数的估计，具体工作流程如图4所示。设离合器滑摩转矩为系统控制量u，离合器滑摩转速为系统输出y。首先，获取k-1时刻的控制输入量u(k-1)和k时刻的系统输出y(k)，通过伪偏导数估计算法计算k时刻的伪偏导数ψ(k)，然后将u(k-1)、ψ(k)和y(k)3个量代入控制率表达式中，计算k时刻的控制量u(k)并施加到DCT系统中。

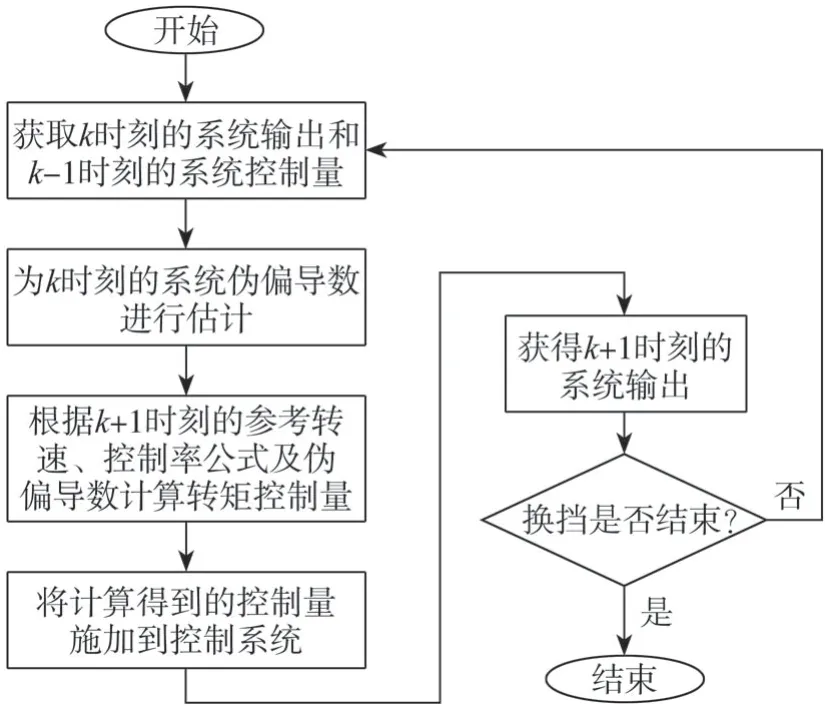
图4 MFAC控制器工作流程框图

2.2 控制率推导

根据MFAC理论，对可用非线性方程描述的DCT系统进行以下假设:

（1）系统真实输出对控制量具有连续的偏导数；（2）系统是可控可观测的；

（3）系统满足广义利普希茨连续条件。

当被控系统满足上述3个假设时，则在k时刻必然存在一个参数ψ(k)，满足下式:

式中:Δy(k+1)为k+1时刻的系统输出与k时刻的系统输出之差；Δu(k)为k时刻的系统控制量与k-1时刻的系统控制量之差。ψ(k)是一个时变参数，被称为伪偏导数，在实际控制过程中，需要对其进行实时估计，以获得DCT系统的动态数据模型。

MFAC控制器的控制目标为消除系统真实输出转速与参考转速之间的误差，实现跟踪控制，同时，由于控制量的变化速度与换挡冲击直接相关，应引入惩罚项对换挡控制量的变化量进行限制。因此，换挡过程控制的目标函数定义为

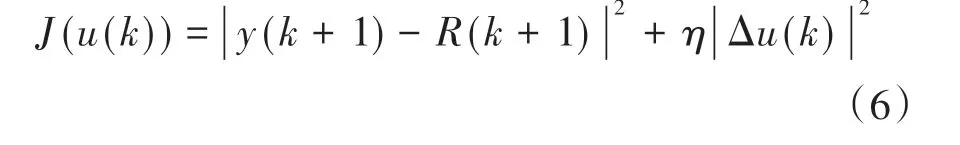
式中:R(k+1)为离合器期望达到的参考转速；η为控制量变化量的惩罚权重。

将式（5）代入式（6）中，并使其对控制量Δu(k)求导，将泛函导数为0所对应的控制量u(k)作为当前时刻的最优控制量，推导出k时刻的控制率如下:

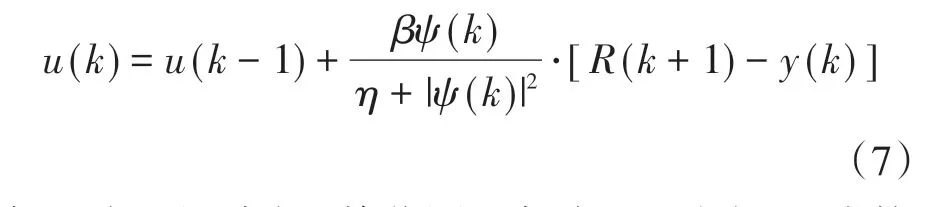
式中:β为可调步长，其范围一般在0～1之间；η为控制量变化权重，防止控制率的某一项分母为0时程序出现错误。

2.3 伪偏导数估计

式（7）中的伪偏导数ψ(k)是一个未知的动态参数，同时也是实现数据驱动控制的核心，因此必须对其进行较为准确的估计。目前已有几类估计算法经调试后具有较高的精度，本文中采用与控制率推导过程相同的极值法进行伪偏导数估计。

根据式（5），伪偏导数估计是为了让ψ(k)Δu(k)与Δy(k+1)的差值尽可能逼近于0，因此，目标函数定义为

式中λ为伪偏导数变化量的惩罚权重，目的是限制伪偏导数变化过快，使其保持在合理的范围内。

对伪偏导数ψ(k)求导，并令导数等于0，得到ψ(k)的估计公式为

式中:ψˉ(k)为ψ(k)的估计值；ζ为可调步长，其范围一般在0～2之间。

在实际控制中，将伪偏导数估计值ψˉ(k)代入到式（7）中，就能得到当前时刻的控制量u(k)，该控制量即为DCT系统的补偿转矩，与参考转矩加权求和后，作为系统输入实现MFAC换挡控制。

3 DCT系统仿真模型

为对所设计的DCT换挡过程数据驱动控制器进行快速验证，并为后续用于对比的基于模型的控制器提供设计依据，根据DCT整车动力学建立DCT系统仿真模型。

由于无模型自适应控制是一种数据驱动控制，控制量只取决于实测的输入输出数据和输出参考值，不依赖于系统的机理模型。因此，仿真模型只用于模拟某种特定参数下的实车运行，不需要十分精确的建模。

DCT系统仿真模型包括发动机稳态转矩仿真模型、离合器滑摩转矩仿真模型、行驶阻力仿真模型和DCT换挡过程仿真模型，DCT系统动力学简图如图5所示。

图5 DCT系统动力学简图

根据发动机实验数据，利用插值法建立发动机稳态转矩模型，如图6所示。

图6 发动机稳态转矩模型

建立离合器滑摩转矩模型如下:

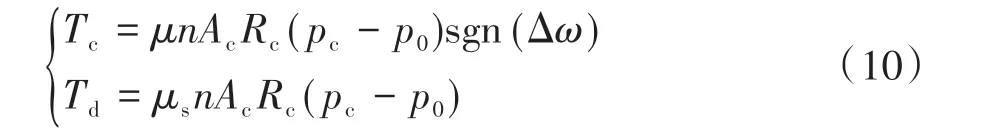
式中:Tc为离合器滑摩状态下传递的转矩；Td为离合器转矩容量；Ac为离合器活塞面积；Rc为离合器等效半径；p0为预充油油压；Δω为离合器主、从动盘的转速差。

行驶阻力模型为

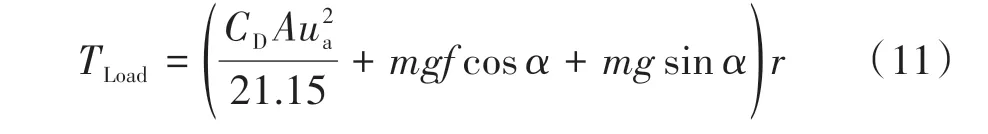
式中:CD为空气阻力系数；A为迎风面积；ua为纵向车速；mg为车辆的总重力；f为滚动阻力系数；α为道路的坡度角。

DCT换挡过程包括转矩相和惯性相。以1挡升2挡为例，在转矩相，离合器1迅速分离，离合器2开始接合；在惯性相，离合器2快速完成同步。

DCT换挡过程转矩相模型如下:

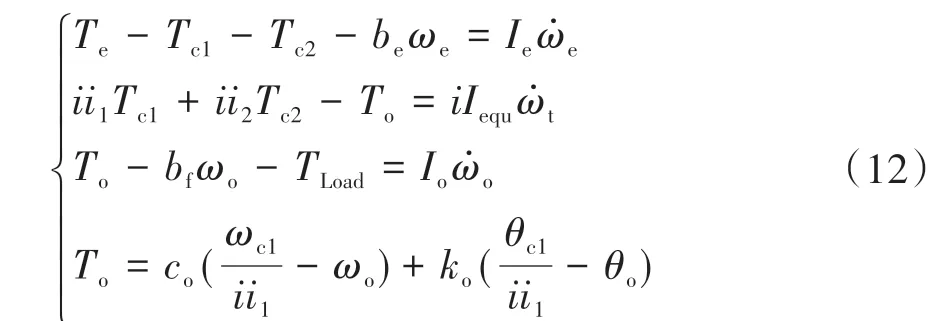
式中:Te为发动机转矩；To为半轴转矩；ωe为发动机角速度；ωt为主减速器从动齿轮角速度；ωc1和θc1分别为离合器1从动盘角速度及对应的角位移；ωo和θo分别为半轴角速度及对应的角位移；i为主减速比；i1和i2分别为1挡和2挡的传动比；be为输入轴的黏性阻尼系数；bf为半轴的黏性阻尼系数；co和ko分别为齿轮系统等效阻尼与刚度；Ie为变速器输入端转动惯量；Io为变速器输出端及整车等效转动惯量；Iequ为齿轮系统等效转动惯量。

式中:Ic1为变速器输入轴1转动惯量；Ic2为变速器输入轴2转动惯量。

DCT换挡过程惯性相模型如下:

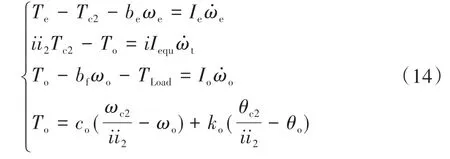
式中:ωc2和θc2分别为离合器2从动盘角速度和对应的角位移。

4 仿真结果分析

在不同油门开度下，对基于数据驱动的DCT换挡过程MFAC控制器的自适应性和鲁棒性进行验证，并与基于模型的控制方法进行对比分析。

基于Matlab/Simulink软件平台，利用S函数模块编写MFAC控制器，并将其嵌入仿真模型中。其中，MFAC控制器的参数如表1所示。

就目前的立法和司法现状来看，虽然我国民事审前程序与其他国家在内容和形式上有所区别，但从程序的角度来说，并无实质性的差异，我们完全可以通过操作层面的改革，借鉴其他国家民事审前程序直接解决纠纷的功能，以实现审前准备程序的庭审准备和纠纷解决的二元性价值。

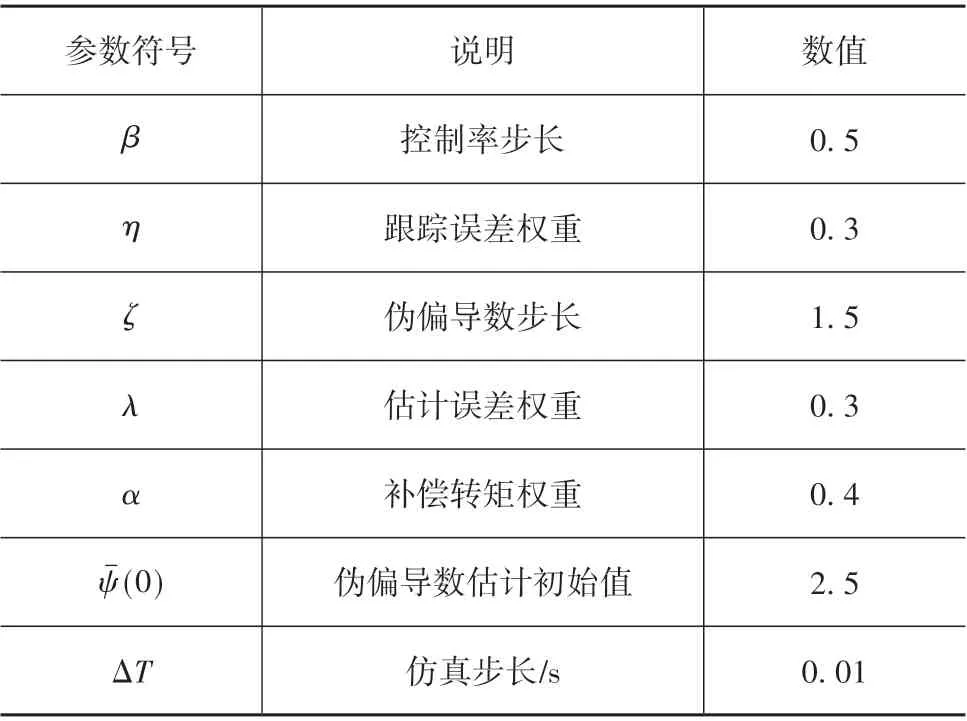
表1 控制器参数

为对比分析数据驱动控制与基于模型的控制，设计了用于DCT换挡过程转速跟踪控制的模型预测控制器（model predictive control，MPC）。MPC控制器的预测模型根据式（10）～式（14）所述动力学模型离散化得到，转速跟踪控制的目标函数同样定义为式（6），滚动优化采用Matlab中的quadprog二次规划函数求解。

首先验证DCT系统性态发生变化后的控制器自适应性。假设整车质量m增加10%，且随着服役时间的增加，离合器产生磨损，相同接合压力pc下离合器传递的滑摩转矩Tc减少5%，同时，发动机也存在一定磨损，相同油门开度下发动机的输出转矩Te减少5%。

按照上述假设对仿真模型进行相应调整，但不改变任何控制器参数。在相同条件下MFAC控制器与MPC控制器的仿真结果进行对比，其中，15%油门开度下升、降挡的仿真结果分别如图7和图8所示。

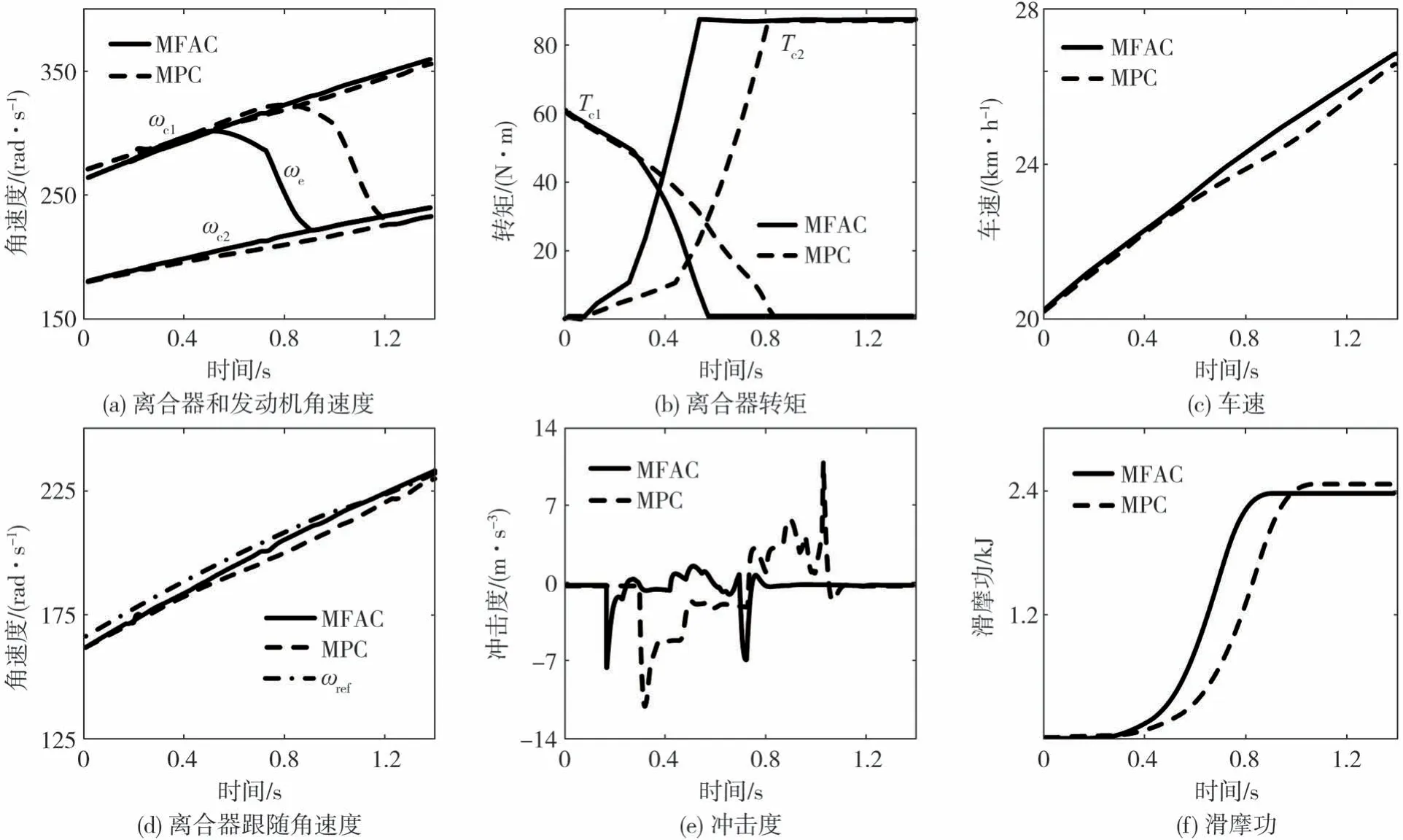
图7 系统性态变化后15%油门升挡对比仿真结果

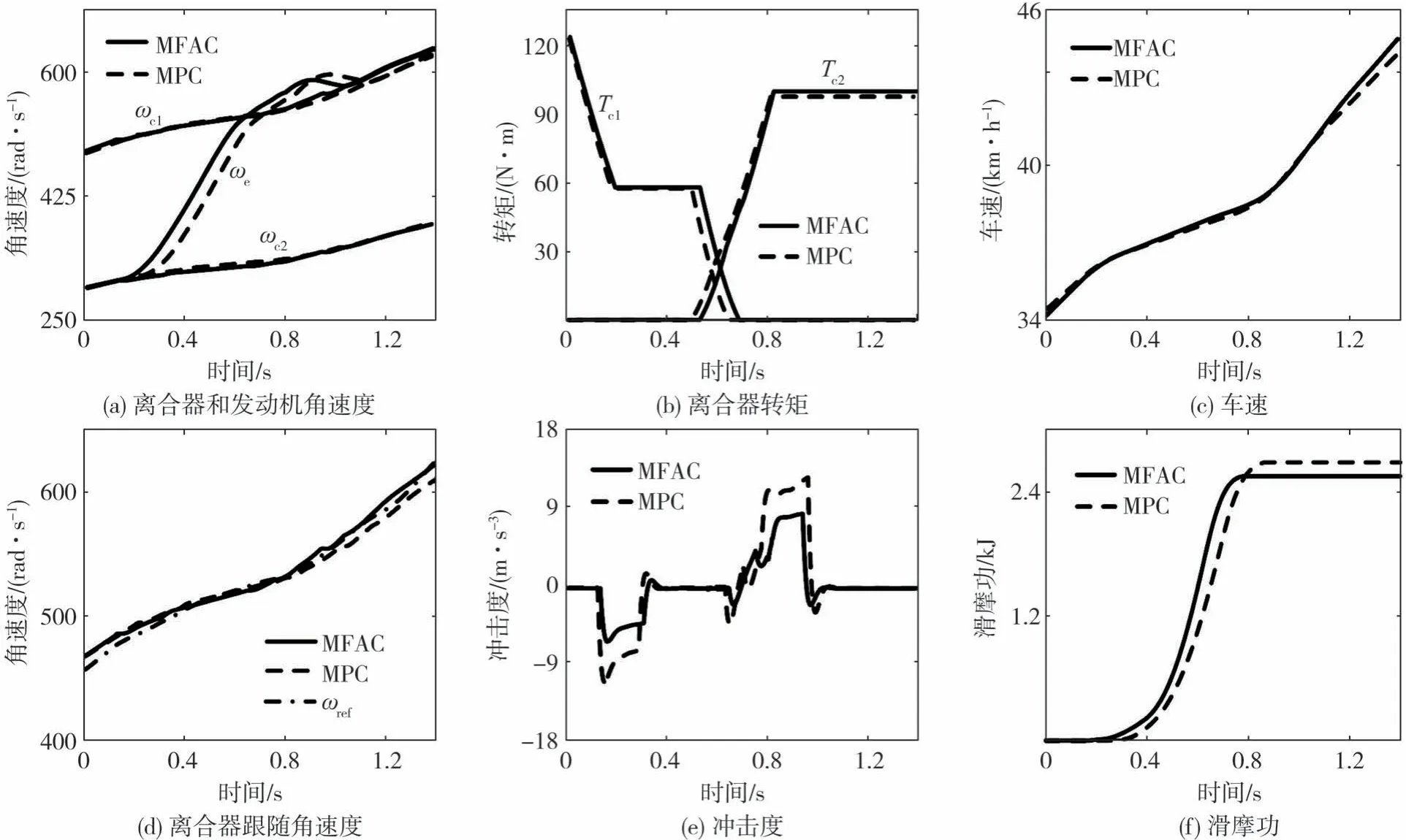
图8 系统性态变化后15%油门降挡对比仿真结果

从图中可知，MPC控制器在模型失准后换挡效果变得较差，离合器真实转速与参考转速间存在较大误差，而MFAC控制器仍保持了良好的换挡性能，离合器真实转速趋近于参考转速，换挡品质受到系统性态变化的影响较小，对模型失准的敏感度较低，具备较强的自适应能力。

接下来验证存在内外部干扰时的控制器鲁棒性。假设整车质量m、离合器1输入轴转动惯量Ic1、离合器2输入轴转动惯量Ic2和变速器输入端转动惯量Ie均存在5%的不确定性，同时，由于转速传感器误差、执行机构控制误差和负载突变等情况，测得的真实转速存在随机干扰信号，如图9所示。

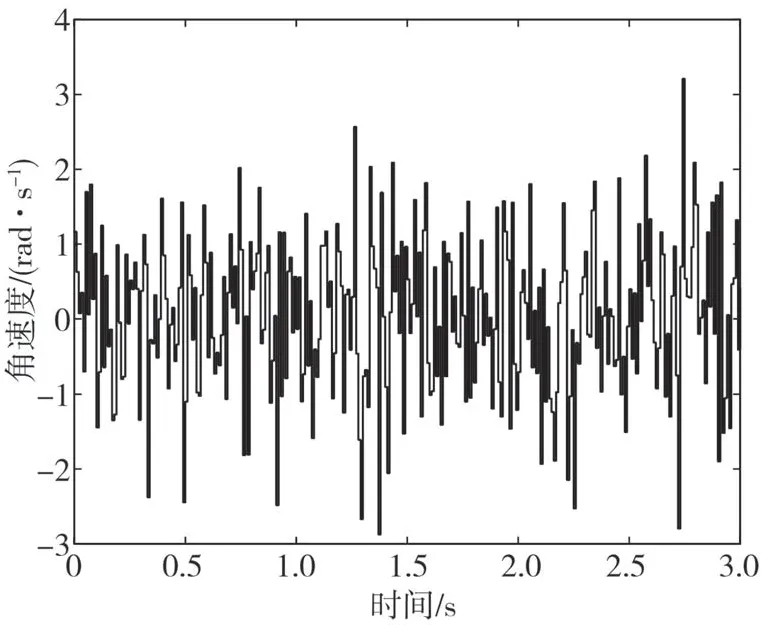
图9 离合器角速度随机干扰信号

按照上述假设对仿真模型进行相应调整，但不改变任何控制器参数。在相同条件下MFAC控制器与MPC控制器进行对比仿真，其中，15%油门开度下升、降挡的仿真结果分别如图10和图11所示。

图10 存在干扰时15%油门升挡对比仿真结果

图11 存在干扰时15%油门降挡对比仿真结果

从图中可知，当DCT系统的输出转速信号存在较大噪声时，MPC控制器对参考转速跟随的效果不佳，且换挡冲击和滑摩功大幅增加，而MFAC控制器未出现失稳，发动机和离合器的控制转矩也未发生突变，虽然转速同样出现了微小的波动，但总体保持平顺，说明该控制器具有较强的鲁棒性和抗干扰能力，在存在内外部干扰时仍能保持良好的换挡品质。

在30%油门和50%油门开度下，上述2种情况的升挡评价指标如表2和表3所示。

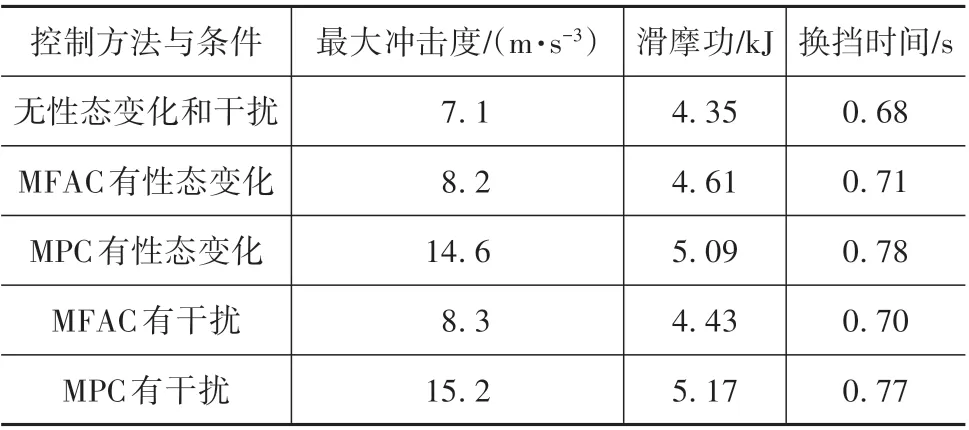
表2 30%油门换挡评价指标对比

表3 50%油门换挡评价指标对比

相同车速下不同油门开度对应着不同换挡意图，从表中可知，在换挡意图变化条件下，MFAC控制器仍能够保持较好的换挡品质。当系统性态发生变化或存在内外部干扰时，MFAC控制器的换挡持续时间变化不大，滑摩功最多增加7.4%，最大换挡冲击最多增加17%，仍在理想范围内。相比之下，依赖机理模型的MPC控制器的最大换挡冲击近乎翻倍，超过了10 m/s3的容许值。

综上，可得出基于数据驱动的MFAC换挡控制器在不同油门开度下，DCT系统性态随服役时间发生改变和存在内外部干扰时，都能保持良好的换挡品质，对系统参数改变具有较好的自适应能力，对内外部干扰具有较好的鲁棒性。