两种常用漂浮式风力机平台动态特性分析
2015-11-18成欣叶舟高月文李春
成欣 叶舟 高月文 李春


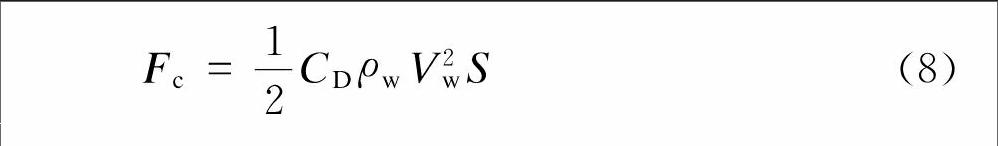
摘 要:分别针对MIT/NREL TLP和UmaineHywind Spar两种海上风力机浮式平台主体的水动力特性进行研究,旨在分析两者的系泊稳定性.基于海洋水动力学和结构动力学理论,建立了平台/缆索系统耦合模型,在水深和外界载荷激励相同的情况下,利用有限元分析ANSYS软件中的水动力学计算模块进行时域、频域响应分析,研究了两种平台在海风、海流和随机波联合作用下的动态响应,并分析了两种平台随波浪频率的响应变化.结果表明:MIT/NREL TLP平台的动态响应较大,而UmaineHywind Spar平台动态响应较小;两平台均在低频波浪作用下产生响应峰值.
关键词:海上风力机; 漂浮式平台; 时域; 频域; 动态特性
中图分类号: TK 83 文献标志码: A
海上有丰富的风能资源和广阔平坦的区域,使得近海风力发电技术成为近年来研究和应用的热点.我国已建成了东海大桥海上风电场,计划建设的近海浅水区域风电场有10多个[1].除渤海外,我国黄海、东海和南海平均水深均在40 m以上,浅水区域有限,非常适合漂浮式风力机系统的开发.海上漂浮式风力机的最大特点是克服了在海床底部安装基础结构时受水深影响的缺点,使海上风电场的建设可向深水区发展[2].在海上风力机平台和开发深海油气的平台中,张力腿平台(TLP)和浮柱式平台(Spar)是公认的优秀平台形式[3].TLP是一种典型的深水平台,以其半固定、半顺应的运动特征在深水海洋工程中广为应用,其最重要的特点是平台的竖向运动很小[4-5].Spar平台属于顺应式平台的范畴,凭借其优良的性能和相对较低的造价,成为世界深海风力机和油气开采的主力平台类型之一[6].近年来,我国风电产业发展迅猛,海上石油开发业从近海走向深海[7],为适应深海平台开发的需要,有关深海平台的相关理论和技术的研究得到了蓬勃发展.
浮式平台的动态特性能够反映平台在外界载荷作用下的响应特性和稳定性,对整个漂浮式风力机系统的稳定性和安全性有重大影响.本文分别选取设计水深相同的MIT/NREL TLP平台和UmaineHywind Spar平台,借助有限元分析ANSYS软件中的水动力计算模块进行时域、频域响应分析计算,分析两种平台在相同风、浪、流作用下的位移动态响应以及平台响应随波浪频率的变化.
1 基本环境载荷
环境载荷指直接或间接由环境作用引起的载荷,包括由环境载荷引起的所有外力,如系泊力、运动惯性力、液舱晃荡力等.漂浮式风力机所受到的环境载荷主要来自风、浪、流,还有内波、地震和海冰(大块浮冰或冰山).本文仅考虑前三种载荷.
1.1 风载荷
海风对海洋结构物的工作影响很大,通常作用在结构上的风载荷是动态的,但一些结构对风载荷的反应几乎为静态形式.在实际工程中常用设计风速法得到结构所受到的海风载荷.根据我国海上移动平台入级规范可计算作用于构件上的风力F,并应确定合力作用点的垂直高度[8],即
式中:S为平台在正浮或倾斜状态时受风构件的正投影面积;Ch、Cs分别为受风构件的高度系数和形状系数;P为风压;V为设计风速.
1.2 波浪载荷
波浪载荷是漂浮式风力机平台所受到的主要环境载荷,且较风载荷更为复杂,这也是与陆上风力机最大不同之处.作用在漂浮式平台上的水动力包括波浪激振力、由结构运动产生的辐射力和考虑波浪高阶效应的漂移力.其中:波浪激振力包括由入射波形成的不稳定压力所引起的F-K力(佛汝德-克雷洛夫力)和由于结构存在影响波浪密度分布产生压差而引起的绕射力;辐射力包括附加质量力和辐射阻尼力.对于大尺度结构,一般采用绕射理论对作用于物体表面上的整个水动压力进行积分计算波浪载荷.在绕射理论中,流场用速度势函数描述,该速度势在流体各处应满足拉普拉斯方程,并满足物体表面、自由表面、海底及无穷远处的边界条件.通常总速度势由入射势、绕射势(假定物体固定)和运动着的物体在静水中产生的辐射势组成,从而得到结构物的运动与作用力.描述波浪运动的理论有许多,根据不同要素可分为线性和非线性、有旋和无旋、规则和不规则、单向和多向、浅水和深水等.漂浮式风力机平台一般远离海岸,局部水深几乎不变;与波长相比,水深相对较大.通常用无旋模型描述一个波浪在其生成区域外的传播或在水池内造波机产生的波浪传播.理想流体和无旋流动的假设可使问题大大简化,其方法是引入速度势函数Φ(x,y,z,t),利用速度势给出速度场V(x,y,z,t)=
Φ(x,y,z,t),于是流动的无旋性自动得到保证.在流域内质量守恒(对于不可压缩流体,divV=0)可表示为速度势函数的拉普拉斯方程[9],即
通过伯努利拉格朗日关系式可得到流域内的压力
式中: p0为参考压力,即大气压力;ρw为海水密度;g为重力加速度.
波浪理论的分类与3个几何参数(波高H、波长L、水深h)有关.浅水理论与深水(或中等水深)理论之间的区别取决于厄塞尔参数Ur,有
式中:A为波幅;k=2π/L;非线性参数ε=A/h;色散参数μ=kh.
当Ur<1,意味着色散效应较非线性效应占优势,用参数kA≡ε对势函数Φ进行展开,可实现对问题的求解,即
式中,(i)为势函数的i阶导数.
这就是所谓的斯托克斯方法,由此可得到斯托克斯规则波模型.相反,当Ur>1,h/L为小参数,从而得到椭圆余弦波模型和孤立波模型.在大部分海洋工程模型中,水深足够大,故可应用斯托克斯模型[10].
小尺度海洋结构上的波浪力Fw通常采用Morison方程计算,由拖曳力和惯性力组成,即
式中:CD、CM分别为曳力系数和惯性力系数;u为垂直于构件轴线水质点的速度分量;D为直立圆柱的直径.
1.3 海流载荷
海流载荷是由海流作用在海洋工程结构物上所产生的载荷.海流力是作用在海洋结构物上的一种流动阻力.根据水下结构物上的阻力是流体动能函数的原理,可按照稳定流动条件下阻力的数学表达式得到海流力,其计算需合理确定海平面以下某深度的海流速度、阻力系数和惯性力系数.其中,海流设计流速应取为在平台作业海区范围内可能出现的最大流速值,包括潮流流速、风暴涌流速和风成流流速,还应考虑作业海区流速的垂向分布.当波浪存在时,还应对无波浪时的流速垂向分布进行修正,以使瞬时波面处的流速保持不变.
当只考虑海流作用时,作用在平台水下部分构件的海流载荷为式中,Vw为设计海流流速.
应注意海流与波浪的相互作用.当采取Morison公式计算波浪载荷时,应将波浪水质点速度与海流速度矢量相加;当采用绕射理论计算波浪载荷时,海流载荷应按式(8)计算,并与波浪载荷矢量相加.
2 平台建模与计算
2.1 平台模型建立
本文研究对象为MIT/NREL TLP和UmaineHywind Spar平台.TLP平台由麻省理工学院设计的张力腿平台改进得到,以混凝土为压舱物,8根缆索分成4组构成4根筋腱,分别连接4根从底部水平延伸而出的辐条和位于海底的桩基,缆索由于预张力作用始终处于完全张紧状态;Spar平台是缅因大学根据国际能源署(IEA)研发的OC3Hywind Spar改变水深以便于试验比较而得来,主体为一深吃水的细长浮筒,周身附连3根悬链线缆索并通过三脚架连接,以增加平台系泊的抗偏刚度,相邻缆索夹角为120°,且在一定预张力作用下处于半张紧半松弛状态[11].
本文采用ANSYS软件中水动力计算模块进行模型导入和表面网格划分,分析中对系泊系统进行了适当简化,忽略了系泊系统的阻力.对UmaineHywind Spar作了去除三角形连接、缆索直接连在浮筒上的简化,这在静态分析中是合适的,但不适用于所有的动态条件[12].计算中没有对缆索进行线性简化.两平台参数如表1所示.图1分别为MIT/NREL TLP和UmaineHywind Spar平台几何模型.
2.2 响应算子与自由度
浮体波频运动6个自由度响应的稳态幅值称为幅值运动响应算子(response amplitude operator).该算子是由波浪激励到船体或浮体运动的传递函数,为船体或浮体运动谱与波浪谱的比值,表征单位波幅的特征响应.对于平动,其幅值响应算子Y2yζ(ω)=Syζ(ω)/Sζ(ω);对于转动,其幅值响应算子Y2θζ(ω)=Sθζ(ω)/Sζ(ω),其中:Syζ(ω)和Sθζ(ω)分别为海上结构物的平动和转动运动谱;Sζ(ω)为波浪谱;ω为入射波浪的频率.
随机波浪可视为无数个振幅、频率不等,初相位随机并沿与x轴成不同角度的方向传播的简单余弦波的叠加.通常把风浪和由此引起的摇荡运动都看成是具备各态历经性的平稳随机过程,平台对任一波浪成分的响应是该成分波波幅的线性函数并与它对其它波浪成分的响应无关.利用平台各自由度的运动幅值响应算子给出在每一个波浪频率下的平台响应并叠加求和,可得到在多个波浪作用下的平台运动方程[13].可用平台位置的幅值响应算子反映在外界环境载荷激励下平台在6个自由度上的运动情况,从而体现平台稳定性.6个自由度上的运动如图2所示.由于风、浪、流均为-180°入射,因此主要分析沿x轴的平动(纵荡)和绕y轴的转动(纵摇)位置幅值响应算子.
2.3 计算工况
在外界激励条件相同时对两种平台进行时域响应分析,风速恒定取为10 m·s-1,设定海流速度从海平面至海底由0.95 m·s-1线性减小至0 m·s-1,随机波谱选择P-M谱,外界海况条件参数如表2所示.利用表2的数据建立平台与缆索在风、浪、流联合作用下的耦合计算模型,分析时间为300 s,时间步长为0.01 s.
3 结果分析
3.1 MIT/NREL TLP平台
3.1.1 时域响应分析
图3(a)、(b)分别为MIT/NREL TLP平台纵荡和纵摇时域位移幅值响应算子,其中纵坐标分别表示对应单位波幅的位移和偏转角.从图3中可看出,平台在风、浪、流载荷作用下绕起始位置作往复运动,纵荡和纵摇运动均在约180 s后开始进入峰值,其中纵荡最大位置幅值响应算子约为5 m·m-1,纵摇最大位置幅值响应算子最大值约为17°·m-1.
3.1.2 频域响应分析
频域响应分析是研究平台随波浪频率变化的运动响应,考虑到载荷的作用方向与平台自身特点,此处分析纵荡、垂荡和纵摇的频域响应.图4(a)、(b)、(c)分别为MIT/NREL TLP平台纵
荡、垂荡和纵摇运动的频域响应算子.从图中可看
出,平台纵荡运动在0.07 rad·s-1左右的波浪频率下产生响应峰值,之后随着波浪频率增大响应急剧降低,约在0.4 ~0.7 rad·s-1之间上升,随后便呈下降趋势;垂荡运动约在波浪频率0.5 rad·s-1时
出现响应峰值,该值前后均为急升急降趋势;而纵摇运动的响应峰值出现在波浪频率0.8 rad·s-1左右;此外,TLP平台的垂荡和纵摇频域响应的峰值接近.
3.2 UmaineHywind Spar平台
3.2.1 时域响应分析
图5为UmaineHywind Spar平台在相同载荷作用下的纵荡和纵摇位置幅值响应算子,其中纵坐标分别表示对应单位波幅的位移和偏转角.从图中可看出,平台在风、浪、流载荷的作用下绕起始位置作往复运动,且比MIT/NREL TLP的运动更为规律.相比于TLP平台,其纵荡位移响应算子均为cm级,平动位移变化很小;由于平台自身结构特性,纵摇位置响应亦很小,最大值不到3°·m-1.
3.2.2 频域响应分析
图6为UmaineHywind Spar平台的纵荡、垂荡和纵摇运动的频域响应算子.由图6可知,
Spar平台纵荡运动在0.07 rad·s-1的波浪频率下即出现响应峰值,且除0.20~0.34 rad·s-1之间有小幅升高外,响应幅值呈下降趋势,且峰值略小于TLP平台的峰值;垂荡运动的响应峰值出现在频率小于0.5 rad·s-1处,峰值较TLP平台的小;纵摇运动的响应峰值出现在频率0.4 ~0.5 rad·s-1之间,
且与TLP平台相比峰值较小;Spar平台的垂荡响应峰值大于纵荡和纵摇的响应峰值.
以上分析说明,在外界风、浪、流载荷作用下:
(1) MIT/NREL TLP平台产生较大动态位移,并引发较大幅度的往复运动和摇摆运动;
(2) UmaineHywind Spar平台动态位移较小,考虑其重心远远低于浮心,稳定性较好;
(3) 两平台的纵荡、垂荡和纵摇运动响应对频率变化均较敏感,并在低频率时出现响应峰值.
4 结 语
本文在给定海况条件下,考虑风、浪、流联合作用,借助有限元分析ANSYS软件中的水动力模块计算分析了两种经典风力机平台的时域和频域响应.当然,由于在计算过程中尚未考虑平台主体与风力机正常运行下的耦合作用,因此实际耦合情况下的稳定性情况尚有待继续分析.若能在后续研究工作中加以解决,并能同时考虑平台与波浪之间的共振效应,则可对这两种经典平台的性能和实用性作出更具现实意义的对比,以期得到在不同海况条件下的最佳平台选择,或者通过对平台的改进以降低危险和建造成本.这将具有更大的实用价值,且将为我国深海漂浮式风力机的发展提供更多有益的参考.
参考文献:
[1] 黄维平,刘建军,赵战华.海上风电基础结构研究现状及发展趋势[J].海洋工程,2009,27(2):130-134.
[2] 高伟,李春,刘全.深海漂浮式风力机的概念设计与气动水动力耦合特性评述[J].能源研究与信息,2011,27(3):168-173.
[3] 唐友刚,张素侠,张若瑜,等.深海系泊系统动力特性研究进展[J].海洋工程,2008,26(1):120-126.
[4] 胡志敏,董艳秋,张建民.张力腿平台波浪载荷计算[J].中国海洋平台,2002,17(3):6-11.
[5] 董艳秋,胡志敏,张翼.张力腿平台及基础设计[J].海洋工程,2000,18(4):63-68.
[6] 王兴刚,孙昭晨,梁书秀,等.水深和螺旋板对Classic Spar水动力特性的影响[J].中国海洋平台,2011,26(1):23-30.
[7] 曾晓辉,沈晓鹏,吴应湘,等.深海平台分析和设计中的关键力学问题[J].船舶工程,2005,27(5):18-21.
[8] 中国船级社.海上移动平台入级规范[M].北京:人民交通出版社,2012.
[9] 唐友刚.海洋工程结构动力学[M].天津:天津大学出版社,2008.
[10] MORLIN B.海洋工程水动力学[M].刘水庚,译.北京:国防工业出版社,2010.
[11] ROBERTSON A N,JONKMAN J M.Loads analysis of several offshore floating wind turbine concepts[C]∥International Society of Offshore and Polar Engineers 2011 Conference,Hawaii,2011.
[12] JONKMAN J.Definition of the floating system for phase IV of OC3[R].NREL/TP-500-47535,2010.
[13] 吴秀恒.船舶操纵性与耐波性[M].2版.北京:人民交通出版社,1999.
