汽车非平稳随机振动统计特性求解的一种新方法*

2021-07-05郭文翠

汽车工程 2021年6期

关键词：挠度车速悬架

李杰，陈涛，郭文翠，赵旗

（吉林大学，汽车仿真与控制国家重点实验室，长春 130025）

前言

路面不平度是沿着道路走向的路面轮廓相对于基准平面的高度变化［1］，反映了道路存在不平的自然和客观状态。路面不平度是道路走向长度的函数，具有平稳随机过程的特性［2］。

路面激励是汽车在道路行驶时的振动输入，反映了路面不平度和车速对汽车的共同作用［3］，也称为路面不平度激励。路面激励是时间的函数，具有随机过程的特性。

当车速不随时间变化时，路面激励具有平稳随机过程特性，对应产生的汽车随机振动，称为汽车平稳随机振动。当车速随时间变化时，路面激励具有非平稳随机过程特性，对应产生的汽车随机振动，称为汽车非平稳随机振动。

汽车平稳随机振动描述的是汽车匀速行驶工况，反映的是汽车匀速行驶的平顺性。然而，除了匀速行驶工况外，汽车还存在着起动、加速和减速等非匀速行驶工况，汽车平稳随机振动研究及其成果不适用于非匀速行驶工况，需要开展汽车非平稳随机振动研究，使其既能适应非匀速行驶工况，也能适应匀速行驶工况。考虑车速变化的汽车非平稳随机振动是更符合汽车实际运行的随机振动，开展汽车非平稳随机振动研究既是汽车平稳随机振动研究的深入，也是非匀速行驶汽车平顺性研究的基础和前提。

Hammond等指出汽车非匀速行驶时路面激励为非平稳随机激励［4］，并且提出建立非平稳路面随机激励模型的协方差等效方法。Harrison等应用协方差等效方法建立了汽车4自由度平面模型的非平稳路面随机激励［5］，说明了协方差等效方法用于汽车4自由度平面模型的可行性。Narayanan等采用协方差等效方法表示非平稳路面随机激励［6］，将其用于研究汽车单自由度单轮模型的非平稳随机振动及其优化。罗明廉等将协方差等效方法用于汽车5自由度平面模型，研究了汽车座椅加速度非平稳随机振动［7］。张立军等以协方差等效方法表示四轮非平稳路面随机激励［8］，随后进行了汽车非平稳行驶动力学和控制的研究［9］。胡启国等将协方差等效方法用于汽车5自由度平面模型［10］，对影响座椅加速度的主要参数进行了仿真分析。然而，由Hammond等提出的协方差等效方法，只能用于求解汽车振动响应，不能用于求解汽车非平稳随机振动的功率谱密度和均方根值。

金先龙研究了非平稳随机振动激励的瞬时功率谱密度，提出了一种非平稳随机振动激励瞬时功率谱密度的表示［11］。赵丁选和刘刚等建立了车辆非平稳随机加速度瞬时功率谱密度和位移功率谱密度之间的关系［12-13］，确定了变车速行驶时车辆非平稳随机加速度的瞬时功率谱密度表示。张立军等提出一种非平稳随机振动响应瞬时功率谱密度计算方法［9］，将时间频率响应特性替换为空间频率响应特性，通过对空间频率进行积分求解响应的瞬时功率谱密度。然而，瞬时功率谱密度方法存在两方面的问题:一方面是只给出理论表示，没有具体应用；另一方面是虽然给出理论表示和具体应用，但理论仍表示存在一定问题。

在前人研究的基础上，本文中基于无论汽车匀速行驶还是非匀速行驶路面不平度都始终具有平稳随机过程的特性，结合汽车振动2自由度单轮模型，建立汽车非平稳随机振动响应统计特性求解的新方法，完成从理论、程序开发到具体应用的全部过程。

1 时间域汽车振动模型

1.1 力学模型

汽车振动2自由度单轮力学模型如图1所示，由车身簧载质量m2、非簧载质量m1、刚度系数为k和阻尼系数为c的悬架、刚度系数为kt的轮胎组成。z2(t)是簧载质量垂直位移，z1(t)是非簧载质量的垂直位移，q(t)是路面激励。

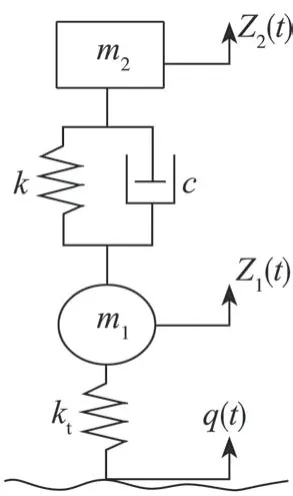
图1 汽车振动2自由度单轮力学模型

1.2 数学模型

针对汽车振动2自由度单轮力学模型，根据拉格朗日方程建立数学模型:

其中:

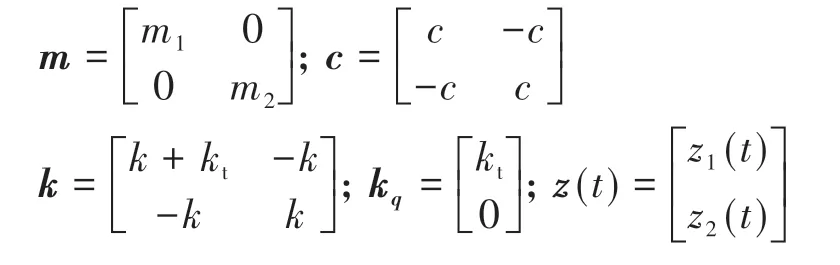
1.3 振动响应量

针对汽车振动2自由度单轮力学模型，将车身簧载质量加速度z̈2、悬架动挠度fd和车轮相对动载Fd/G作为振动响应量［1］。

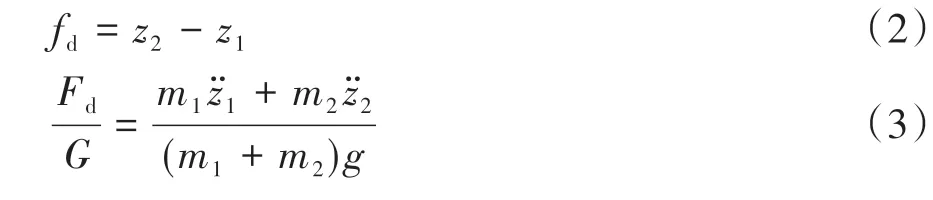
2 空间域汽车振动模型

2.1 变量及其导数的变换关系

设变量z为变量s的函数z=z(s)，而s又为变量t的函数s=s(t)，则z既是变量s的函数又是变量t的函数，即

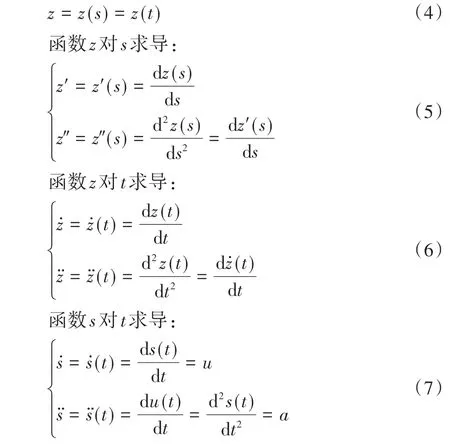
在式（7）中，引入u和a表示s对t的1阶导数和2阶导数。如果s是行驶距离，则u和a分别为行驶车速和行驶加速度。

针对z→s→t的复合函数，根据复合函数的导数运算法则有

将式（4）和式（8）推广到向量得

2.2 空间域汽车振动模型推导

将式（9）代入式（1）有

式（11）是空间域汽车振动模型，当u不随着时间t变化时，其为时不变系统，即M、C和K不随着时间变化；当u随着时间t变化时，其为时变系统，即M、C和K随着时间变化。

3 空间频率响应特性

3.1 汽车振动空间频率响应特性

在空间域内，设n是与行驶距离s对应的空间频率，依据傅里叶变换得

式中:z(n)为z(s)的傅里叶变换；z′(n)为z′(s)的傅里叶变换；z″(n)为z″(s)的傅里叶变换；j= -1。

对式（11）两端进行傅里叶变换，结合式（12），汽车振动空间频率响应特性H(n，t)为

应当说明的是:如果u为t的函数，则H(n，t)既为n的函数，也为t的函数；如果u为常数，则H(n，t)变成H(n)，只为n的函数。

3.2 汽车振动空间频率响应特性展开

对于汽车振动2自由度单轮模型，将m、c和k的具体表示代入式（14）展开和推导。

其中:

3.3 时间域加速度的空间频率响应特性

为了简化表示，省略函数括号中的自变量t或s。对于任意响应z，由式（8）得

3.4 振动响应量的空间频率响应特性

4 振动响应量统计特性

4.1 路面不平度的空间域统计特性

路面不平度q(s)是行驶距离s的函数，其空间域统计特性由空间频率谱密度Gq(n)描述，根据路面分类标准表示为［1］

式中:Gq(n0)为路面不平度系数，由路面分类标准给定［1］；参考空间频率n0=0.1 m-1；频率指数W=2。

4.2 响应和激励的统计特性关系

设平稳随机过程q=q(s)，如果s=s(t)，则由s=s(t)代入q=q(s)得到的q=q(t)就变成特殊的非平稳随机过程。在随机振动理论上，这样的非平稳随机过程q=q(t)称为演变随机过程，由此建立了演变随机过程功率谱密度方法［14-17］。

再设q=q(t)为激励，z=z(t)为响应，则z=z(t)也变成特殊的非平稳随机过程。如果将z=z(t)变换到s的空间频率n所在空间域内，则响应和激励的空间频率响应特性就变成n和t的函数，即H(n，t)z-q。

如果Gz(n，t)为响应的功率谱密度，σz(t)为响应的均方根值，则［14-17］

式中nl和nu为空间频率n的下限和上限。

4.3 振动响应量的时变统计特性

由式（25），各个振动响应量的时变功率谱密度为

5 振动响应量统计特性求解

5.1 汽车参数和行驶工况设置

针对前述理论分析，本文中采用Matlab开发了汽车非平稳随机振动响应量统计特性求解仿真程序，在给定汽车参数、车速时间变化序列和行驶距离初值，选择路面标准给定的任何等级路面后，通过仿真就可以得到车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的功率谱密度和均方根值。

对于汽车振动2自由度单轮模型，采用某汽车参数［18］，m2=878.8 kg，m1=106 kg，k=184082 N/m，c=3 292.8998 N·s/m，kt=762900 N/m。

选择汽车典型行驶工况，如图2（a）所示。由变化的行驶速度和行驶距离初值，可得到汽车的加速度和行驶距离，如图2（b）和图2（c）所示。由图可以看出:首先汽车匀加速行驶，加速度为1 m/s2；然后汽车匀速行驶，加速度为0；最后汽车匀减速行驶，加速度为-1 m/s2。

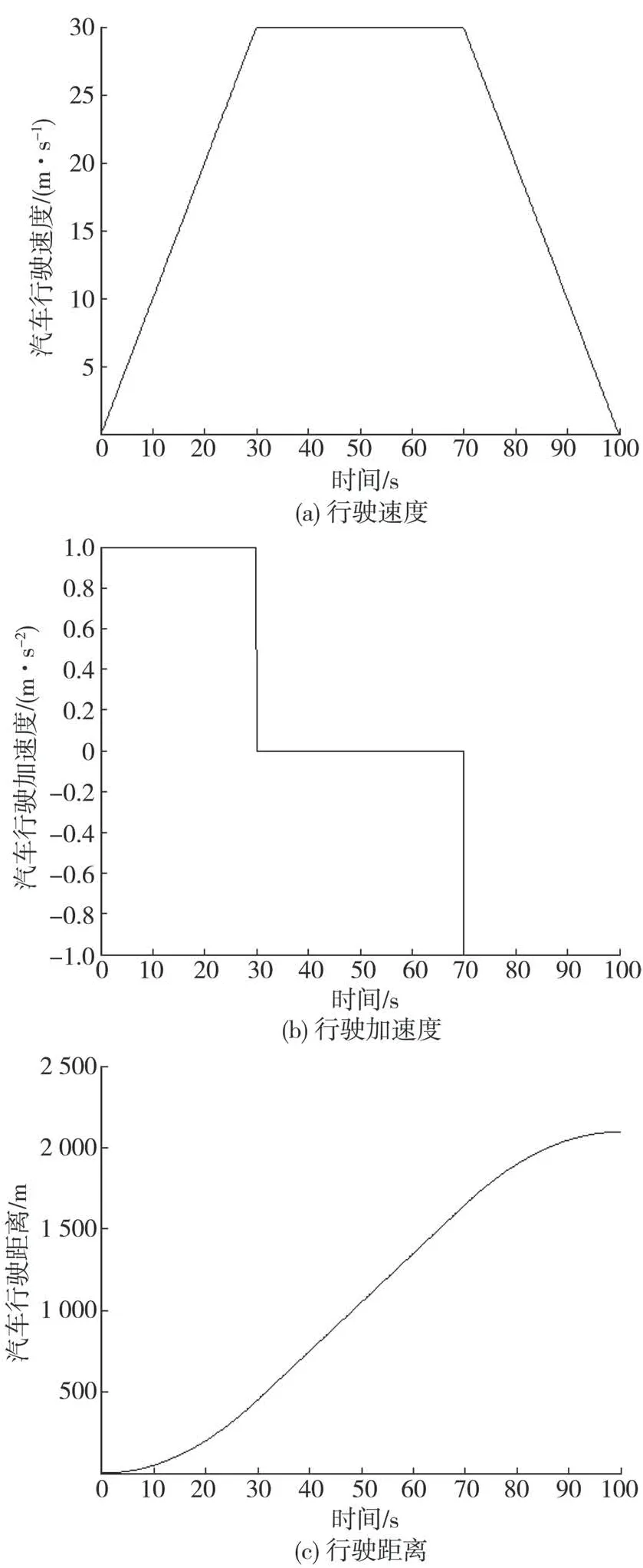
图2 汽车典型行驶工况

5.2 结果分析

对应于典型行驶工况和国内常见的B级路面，非平稳振动响应量的功率谱密度如图3所示。

图3 非平稳振动响应量的功率谱密度

由图3可以看出:非平稳振动响应量的功率谱密度不仅与时间有关，也与空间频率有关；在匀加速行驶时间内，随着车速增加，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的功率谱密度也逐渐变大；在匀速行驶时间内，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的功率谱密度保持不变；在匀减速行驶时间内，随着车速减小，车身簧载质量加速度、悬架动挠度和车轮相对动载的功率谱密度也变小；在匀加速行驶结束和匀减速行驶开始的小段时间内，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的功率谱密度均在较低空间频率时出现波动，说明加速度和减速度对车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的功率谱密度有影响。

由图4可以看出，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的均方根值随着时间变化情况与车速随着时间变化情况相似。在匀加速行驶时间内，随着车速增加，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的均方根值也逐渐增加；在匀速行驶时间内，车速保持不变，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的均方根值也保持不变，符合以往匀速行驶时平稳随机振动响应量为常量的规律；在匀减速行驶时间内，随着车速减小，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的均方根值逐渐变小；在匀加速行驶结束和匀减速行驶开始的小段时间内，车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的均方根值出现小幅波动，说明加速度和减速度对车身簧载质量垂直加速度、悬架动挠度和车轮相对动载的均方根值有影响。