基于樽海鞘算法的教育资源分配

张李玉，贺兴时，杨新社

(1.西安工程大学 理学院，西安 710048；2.密德萨斯大学 科学与技术学院，英国 伦敦 NW4BT)

教育资源配置的均衡化不仅是关乎我国教育事业发展的战略问题，也体现着教育的公平公正。[1]教育的公平公正对于每个人的发展是极其重要的，它决定着个人在未来竞争中的处境，进而因代际传承作用影响到其下一代的发展。[2]公平教育的基本含义就是教育资源能够均等地分配给教育机构和教育群体以 达到教育需求与教育供给的相对均衡。[3-4]教育资源分配的不均衡会导致各种社会问题，如高考移民、社会补习机构的不正规操作等等[5-6]，因此教育资源的均衡分配无论是对当前我国高等教育的发展还是对整个社会的发展都是一项十分严峻的挑战。[7]当前在教育均衡化发展的进程中，大数据技术可以帮助决策管理部门无论是在教育资源的数量上还是教育资源的质量上都能达到最优的分配方案，在教育均衡化发展方面起到重要的影响作用。[8-9]传统的教育资源配置存在分配速度慢、分配不均衡等诸多问题，大数据技术下的分配模型通过对收集到的教育资源数据进行分析和挖掘，有针对性地调整教育资源配置，促使教育资源均衡化发展。所以文章基于樽海鞘算法建立了新的教育资源分配模型，以此来提高教育资源的均衡分配，通过运用樽海鞘算法对假想教育资源分配数据进行数学建模，并将其分配到各个学校使之趋于均衡化，并对实验结果进行对比分析，提出建议。

1 樽海鞘算法

1.1 樽海鞘算法原理

2017 年SEYEDALI Mirjalili 等受樽海鞘在海里群体捕食的生活习性的启发提出了樽海鞘群算法。该算法采用链式结构，链的前端是领导者个体，其余部分是追随者个体外加一个虚拟的移动食物源。[10]因此，樽海鞘算法的基本思想就是通过追踪虚拟的移动食物源来逼近全局最优，实现目标的优化。作为一种新的元启发式算法樽海鞘相较于其他算法来说具有很多优点，比如算法的本身仅有一个主要的控制参数并且计算量小易于操作。算法因为追踪者的渐进运动很难陷入局部最优并且还可以保存当前最好的解，并将其赋值给食物源使得解不会丢失；而且随着迭代的进行控制参数自适应地减小，控制领导者个体在当前食物源周围进行探索和开发[11]。这些优势使得该算法在提出之后很快被广泛研究和应用。文献[12-13]将樽海鞘算法应用于实际问题中，比如参数识别[14]、图像处理[15]、数据挖掘[16]等，证明樽海鞘算法在实际问题中具有很广泛的应用性。

1.1.1 种群初始化

种群的数量表示为N，空间维度表示为D，目标空间则表示为N×D。樽海鞘的位置表示为Xi，所以每个樽海鞘的位置可表示为Xi=[Xi1,Xi2,Xi3,…,XiD],i=1,2,3，…,N;其中虚拟的移动食物源也就是樽海鞘的目标定义为F=[F1,F2,F3,…,FD]；各维度搜索范围的上下界分别为Ub=[ub1,ub2,ub3,…,ubD]以及Lb=[lb1,lb2,lb3,…,lbD]。则初始的种群位置如式(1)表示

XN×D=rand(N,D)×(Ub-Lb)+Lb。

(1)

1.1.2 领导者的位置更新

领导者按照式(2)进行更新

(2)

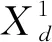
c1=2e-(4×l/lmax)2。

(3)

其中：c2，c3是在[0，1]上产生的随机数，决定领导者位置更新的方向和步长。

1.1.3 追踪者位置更新

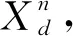
(4)

(5)

1.2 樽海鞘算法步骤

Step 1：随机初始化种群中N个个体教育资源分配方案；

Step 2：计算每一个樽海鞘位置的适度值，目标位置即最优的分配方案F为最小的适度值；

Step 3：根据式(2)和式(5)更新领导者和追随者的位置，计算每一个位置的适度值，并与当前目标位置的适度值相比较，以最小适度值的位置更新最优的方案；

Step 4：不停地迭代重复步骤3，直到迭代次数最大时停止循环并输出当前最优方案。

2 基于樽海鞘算法的教育资源分配模型

我们根据樽海鞘算法步骤1.2中的Step 3设计分配方案。适应度函数的考核标准为各高校比值的均方差大小。初始适应度总值Y=0，分配前各高校的资源数表示为Mi，各高校分配资源数表示为mi，各高校的学生总人数表示为ni，则适应度可以表示为式(6)

(6)

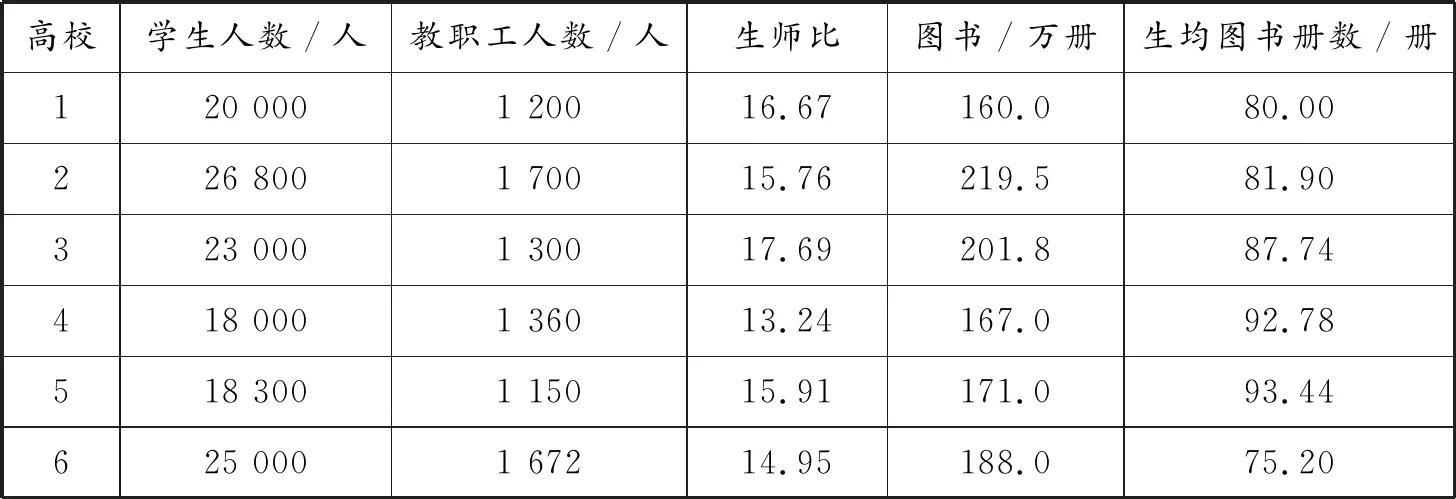
表1 西安市6所高校学生人数、教师人数、图书册数统计表

分配教育资源之前，首先要做的是对各学校现有资源配置的真实调研，在资源分配的过程中，主要目的为均衡各学校之间的资源配置差异，并且以改善现有的资源配置差异情况作为实验结果的优劣分析。

表1中的生师比表示的是学校学生总人数与学校在职的专职教师总人数之间的比值，比值越小则反映该校的专职教师配置情况越好。生均图书册数是该校的总图书册数与总体学生人数的比值，比值越高则反映该校每个学生平均拥有的图书册数越大，即表1中生均图书册数在理论上越大证明该校的图书配置情况越好。结合表1中所统计的6所高校的资源配置情况可以看出，各高校之间的各项配置情况存在较大差异，生师比最大的是高校3为17.69，最小的是高校4为13.24，相差4.45，也就是说高校4平均每个教师要比高校3的多负责4.45个学生而生均图书册数最大的是高校5，为93.44，最小的是高校6，为75.2，相差18.24，也就是说高校5平均每个学生要比高校6的学生多拥有18.24册图书，说明目前教育资源的配置还是处于不均衡的状况。

假设当前有教师1 000名以及新图书10万册需要分配到这6所高校中，为降低生师比较高的高校以及升高生均图书册数较低的高校，以改善统计中这6所高校的教育资源配置，达到较为均衡的状态，我们使用以下方案。

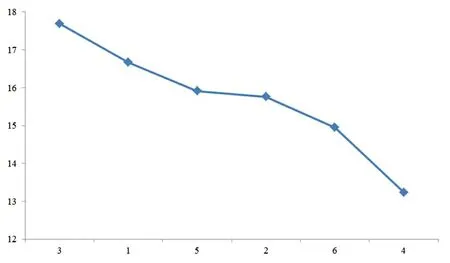
图1 分配之前生师比情况

3 实验过程及结果分析

首先对假设中的1 000名教师进行教育资源分配，将这6所高校的生师比由大到小排序并绘制折线图，如图1所示，图1反映出这6所高校的生师比还是存在较大差距的。

使用基于樽海鞘算法的分配模型对这1 000名待分配的教师进行最优化分配，分配模型的宗旨为均衡各高校的教师资源现状使其达到分配均衡，分配结果如表2所示。

表2 各高校教师分配前后教师人数及生师比变化情况

从表2可以看出，有5所高校不同程度地分配到了新教师，仅有一所高校在前期生师比比较小未分配到新教师，通过进行智能化分配，使得这6所高校的生师比得以均衡化，智能化分配前后的生师比变化趋势折线图如图2所示。

图2 各高校分配前生师比与分配后生师比对比

从各高校分配前后生师比的对比中可以得到，通过此智能分配模型的假想资源分配，可以比较有效地改善各高校在教师资源上的教育资源分配不均衡问题，使得分配之后教师资源达到了较为平均的情况，改善了教师方面教育资源不均衡的问题。

然后对假象的图书资源进行分配，将各高校的生均图书册数从大到小进行排序并绘制折线图，如图3所示。

图3 各高校分配前生均图书册数

图3反映出这6所高校的生均图书册数差异较大，最多的高校5与最少的高校6在图书配置上生均图书相差18.24册，因为这6所高校的教育水平是很接近的，所以存在这样大的差值是不科学的，也从侧面说明教育资源的均衡配置存在较大问题。通过基于樽海鞘算法的分配模型对这10万册待分配的图书进行最优化分配，分配模型的宗旨为减少各高校的生均图书比相差较大的现状，分配结果如表3所示。

表3 各高校图书分配前后图书册数及生均图书比变化情况

从表3可看出，这6所高校都或多或少地分配到了新图书，之前生均图书册数较少的几所学校比起之前生均图书册数相较高的学校上升的幅度更大，随着时间的推移，我们相信国家的教育资源配置也会越来越均衡，现将各高校图书分配前后图书册数及生均图书比变化情况绘制成折线对比图，如图4所示。

图4 各高校分配前后生均图书册数对比

从图4中可以看出，这6所高校在进行分配之后生均图书册数并不是很均衡。造成这种状况的主要原因可能是分配之前这6所高校的总图书册数基数都为几百万，数量比较大，所以模型中假设的分配图书册数较之前各高校拥有的图书册数来说还是太少，想通过分配这10万册新图书来明显地改善生均图书册数不均衡的现状还是有困难的。这也就说明想从根本上改善由于基数过大而造成的教育资源不均衡的问题，应提前预想教育资源分配是否均衡化，而不是亡羊补牢。

教育资源分配总体来说是一项十分复杂、烦琐的工作，随着分配范围的扩大，整个学校,整个城市,整个省甚至到整个国家的教育资源分配，都是需要一套智能化的技术来支持的，因为即使小的范围人为地分配都会存在误差或者错误，更别说分配的范围慢慢扩大了，所以要想在教育资源分配的过程中，改善教育资源配置差异化的问题，必须要借助大数据技术的支持。通过基于樽海鞘算法的分配模型对教育资源进行智能优化分配，在可以不添加人为因素的决策分配中算出各高校的资源现状，教育资源达到最优化的分配结果，从而改善教育资源不均衡的问题。优化智能分配算法为资源分配决策部门提供科学支持，使得分配策略达到均衡化。

4 应用与展望

随着教育现代化水平的不断进步，信息化的教育决策、教育分配也在现实中不断趋于成熟,使得教育教学资源分配变得更加科学。通过建立改进樽海鞘算法的教育资源分配模型对现有的这6所学校存在的教育资源不均衡问题进行改善，并且所建立的模型操作简单便捷，值得推广。

结合各学校教育教学配置现状，建立的大数据技术支撑下教育资源配置模型对教育资源配置更为科学准确。教育资源配置的均衡发展关系着中国教育发展整体性战略布局，随着待分配对象的不断增加，科学地分配模型不仅可以解决人为分配所造成的误差，还可以节约时间，提高教育资源分配任务的效率，这种智能算法的资源配置模型对我国教育资源的均衡化发展有着很大的促进作用。