一般三棱镜最大顶角与折射率的关系
2022-05-30王梦影顾菊观徐海斌
王梦影,顾菊观,徐海斌
(湖州师范学院 理学院,浙江 湖州 313000)
0 引 言
光学教材[1]和光学实验教材[2]对三棱镜的讨论都是针对等边三棱镜在空气中折反射情况的.文献[3]讨论了等边三棱镜偏向角与顶角的关系,获得了棱镜的最大顶角.文献[4]讨论了等边三棱镜在两边折射率为空气的情况下,不同的顶角和棱镜折射率对最小偏向角的影响.文献[5]讨论了等边三棱镜的入射角、棱镜顶角、折射率的变化对偏向角的影响.文献[6]~[8]讨论了等边三棱镜的顶角、最小偏向角、折射率、入射角,以及中空食盐水棱镜的折射率和色散的测量.教材和参考文献几乎没有涉及一般三棱镜及折射率不同的研究.本文主要研究一般三棱镜在顶角和两侧折射率或棱镜折射率不同情况下的最大顶角,并运用几何光学理论、Matlab曲线进行分析讨论,同时与等边三棱镜、等腰三棱镜进行比较.
1 理论分析
1.1 最小入射角
在三棱镜实验中,要求光从AB面入射,在AC面观察到出射光线,并进行测量和计算.如图1,当光入射到AB面的入射角大于一定角度时,在AC面会发生全反射,则在AC面就没有出射光线.因此,对应AB面的入射角不能小于一定角度,否则实验无法进行.

图1 一般三棱镜的光路图(在AC面产生全反射)Fig.1 Schematic diagram of optical path of general prism (in case of total reflection of AC surface)
如图1,由几何关系得:
r1+r2=A.
(1)
由折射定律得:
(2)
当i2=90°时,对应AB面的入射角为最小:
(3)
(4)
因此,当AC面的出射光线沿AC出射时,对应AB面的最小入射角i1min为:
(5)
最小入射角i1min与一般三棱镜角B、C无关,只与一般三棱镜的顶角A和棱镜两侧折射率有关.
当n1=n3=1时,
该结果与文献[3]和[5]一致.

即
(6)
1.2 最大顶角
1.2.1 顶角与折射率的关系
由式(6)可得:
(7)
化简得:
(8)
(9)
(10)
1.2.2 折射率的要求
n1
(11)
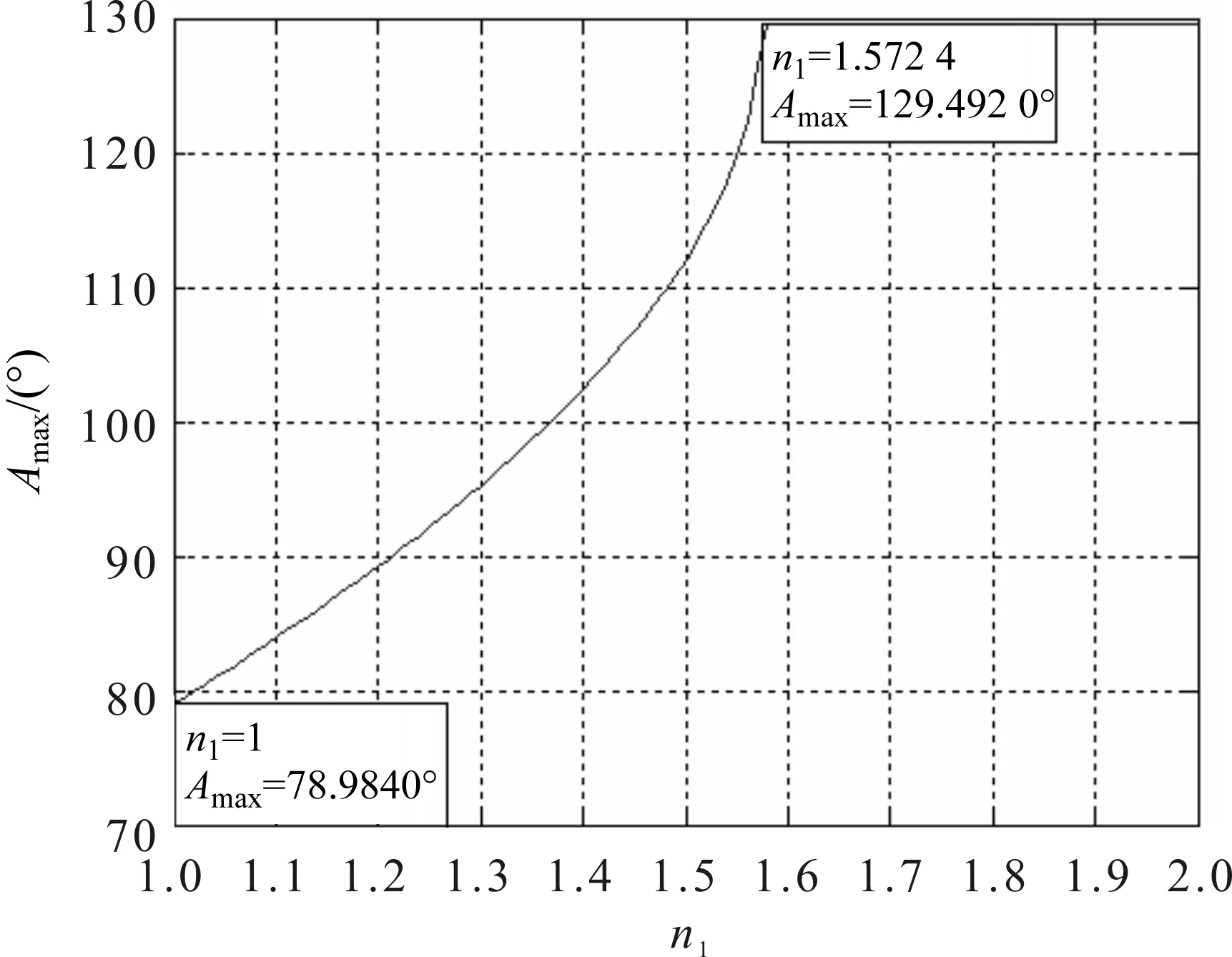
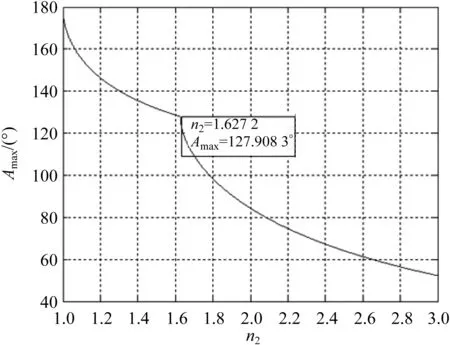
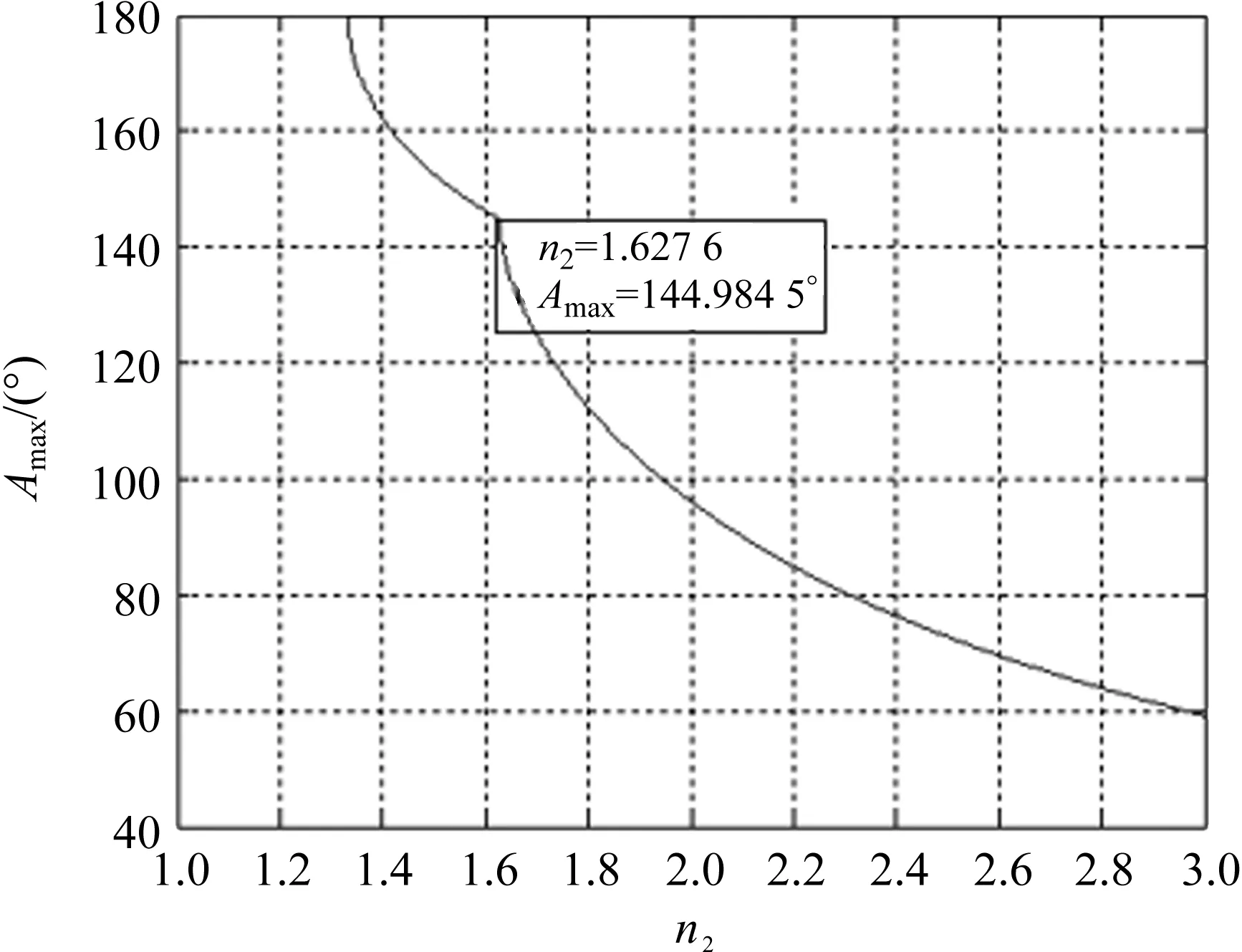
n1>n2 (12) 对式(12),当光从AB面入射时,在AC面不可能产生全反射,而在AB面可以产生全反射(图2(a)),这不能满足题意(在AC面产生全反射)要求,故舍去这个条件.因此,对这种情况,不能用测量最小偏向角(偏向角定义为出射光线以锐角逆时针转至入射光线对应的夹角,且为正值)的方法来计算棱镜的折射率,应用测量入射角和出射角的方法来计算(图2(b)). 图2 一般三棱镜折反射情况(n1>n2 在选择棱镜折射率和两侧折射率时,若要求在AC面观察到出射光线,且能用最小偏向角法测量折射率,则须满足式(11)的要求. 1.2.3 最大顶角 由式(10)将式(9)表示为: (13) 满足式(13)的条件为: (14) 经运算得: (15) 或 (16) 经运算得: (17) 式(15)和式(17)都要满足条件式(11).在式(11)条件下,式(17)对应的顶角A等于或接近180°(若n1=n3=1 一般三棱镜的顶角A应满足式(15),才能满足式(13),此时最大顶角为: (18) 式(18)表明了棱镜最大顶角与棱镜折射率、两侧折射率的关系,即棱镜最大顶角与折射率的关系是非线性的. 根据式(18),应用Matlab可以得到最大顶角与折射率的关系曲线. 当n1=1、n3=1、n2=1.572 4时,对应的三棱镜最大顶角与棱镜折射率的关系曲线如图3所示.由图3可知,当n2=1时,Amax=180°,这相当于在同种介质中,光沿着直线传播,且没有折射;当n2=1.572 4时,对应的棱镜最大顶角为Amax=78.984 0°,且棱镜的最大顶角Amax随着n2的增大而非线性地减少.这为三棱镜顶角和折射率的选择提供了参考,即给定的棱镜折射率对应的顶角不能大于理论得到的最大顶角,否则无法应用最小偏向角法进行实验和研究. 由图4可知,当1≤n1<1.572 4时,棱镜的最大顶角Amax随着n1的增大而非线性地增大;当n1=1.572 4时,Amax=129.492 0°,相当于平面一次折射(光密介质到光疏介质),而非三棱镜的两次折射;当n1>1.572 4时,不能满足条件式(11),则Amax无值. 图3 棱镜最大顶角Amax与棱镜折射 率n2的关系曲线(n1=1,n3=1)Fig.3 Relation curve between maximum vertex angle of prism Amax and refractive index of prism n2(n1=1,n3=1) 图4 棱镜最大顶角Amax与折射率n1的 关系曲线(n2=1.572 4,n3=1)Fig.4 Relation curve between maximum vertex angle of prism Amax and refractive index of prism n1(n2=1.572 4,n3=1) 由图5可知,当n3=1.572 4时,Amax=129.492 0°,相当于平面一次折射(光疏介质到光密介质),而非三棱镜的两次折射. 由图6可知,当n2<1.627 6时,不满足式(11)的要求,Amax也不满足本文题意的要求;若满足式(11)的要求,折射率须满足n2>1.627 6,且Amax随着n2的增大而非线性地减少;当n2=n1=1.627 6时,相当于一次平面折射,此时Amax=127.908 3°. 图6 棱镜最大顶角Amax与折射率n2的 关系曲线(n1=1.627 6,n3=1)Fig.6 Relation curve between maximum vertex angle of prism Amax and refractive index of prism n2(n1=1.627 6,n3=1) 由图7可知,当n2≥1.627 6时,满足式(11)的要求,且Amax随着n2的增大而非线性地减少;当n2取值在1~1.333 0之间时,满足式(12)的要求,不满足本文题意的要求;当n2的取值在1.333 0~1.627 6之间时,不满足式(11)或式(12)的要求,也不满足本文题意的要求. 图7 棱镜最大顶角Amax与折射率n2的关系曲线(n1=1.627 6,n3=1.333 0)Fig.7 Relation curve between maximum vertex angle of prism Amax and refractive index of prism n2(n1=1.627 6,n3=1.333 0) 本文运用折射和全反射定律推导一般三棱镜的最小入射角与顶角的关系,以及棱镜最大顶角与折射率的关系,并运用Matlab得到了棱镜折射率、两侧折射率、棱镜最大顶角的选择范围及其相互之间的关系曲线,其理论分析与模拟结果一致.本研究能够加深学生对一般三棱镜的偏向角与顶角、折射率等关系的理解,提高学生的创新实验设计能力和Matlab软件应用能力.研究结果可为教学、实验和研究中棱镜顶角和折射率的选择、棱镜仪器的设计等提供理论依据.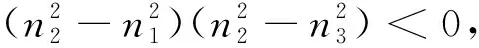


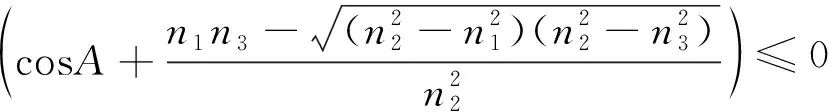
2 利用Matlab模拟最大顶角与折射率的关系
2.1 三棱镜顶角与棱镜折射率的关系曲线(在空气中)
2.2 棱镜最大顶角与折射率n1的关系曲线

2.3 棱镜最大顶角与折射率n3的关系曲线
2.4 棱镜最大顶角与折射率n2的关系曲线(n1=1.627 6,n3=1)
2.5 棱镜最大顶角与折射率n2的关系曲线(n1=1.627 6,n3=1.333 0)
3 结 论
