基于NSGA-Ⅱ算法的低通滤波器优化

袁 爱 霞，房 少 军，刘 浩 然，段 云 梦

(1.大连海事大学 信息科学技术学院，辽宁 大连 116026；2.大连工业大学 信息科学与工程学院，辽宁 大连 116034)

0 引 言

无线通信系统中，滤波器性能的优劣影响到一个通信设备的整体质量，因此，对滤波器性能的优化提出了更高的标准[1]。LC滤波器的优化是一个多约束、非线性的规划问题[2]。该问题具有目标相互耦合，互相制约的特点。如需得到最优解，运算量大，传统的运算已经无法满足滤波器优化的要求。国内外学者采用不同的算法对各类型滤波器进行了优化，如基于混沌遗传算法、量子遗传算法、自适应遗传算法的滤波器优化[3-5]。

NSGA-Ⅱ算法是在第一代非支配排序遗传算法改进的多目标优化算法，提出了精英保留的策略，扩大了种群迭代的选择范围，避免了最优个体的缺失，提高了算法的运行速度，很大程度地降低该算法计算过程的复杂度，改进了传统算法的性能[6]。目前对NSGA-Ⅱ算法进行了较多的研究[7-14]。Zhang等[8]利用改进的NSGA-II完成了对陷波器的多目标优化设计，引入了不同目标重要性向量；肖怀硕等[10]基于改进的NSGA-Ⅱ对故障限流器进行了配置优化，提出了局部微分法提高搜索能力。但没有关于如何选取最优解的论述。因此，提出了一种采用NSGA-Ⅱ算法，对滤波器的多个目标进行优化设计的方案。

本研究针对一个截止频率为50 MHz，特征阻抗为的50 Ω的5阶π形定K型低通滤波器，用NSGA-Ⅱ算法进行了优化。算法首先设定初始化种群，对算法中群体的多样性和全局搜索能力进行改进，确定适应度函数和目标函数，建立约束条件，对滤波器的插入损耗、反射损耗、群时延进行优化；并完成优化结果的仿真与性能分析，优化后的滤波器性能较初始设计有了明显的改善。

1 优化前滤波器性能分析

截止频率50 MHz，特征阻抗50 Ω的5阶π形定K型低通滤波器[15]，如图1所示，这种滤波器存在着截止频率不准确、性能较差等问题。但是这种滤波器元件种类少，级数易于增加，制作简单。如图1所示低通滤波器的仿真结果为插入损耗3 dB，截止频率为45.6 MHz，不是初始计算时规定的50 MHz截止频率，如图2所示。因此针对这个滤波器的截止频率不准确等性能指标进行优化，使滤波器更加符合需求。

图1 5阶π形定K型低通滤波器Fig.1 Fifth order π-shaped fixed K-type low pass filter

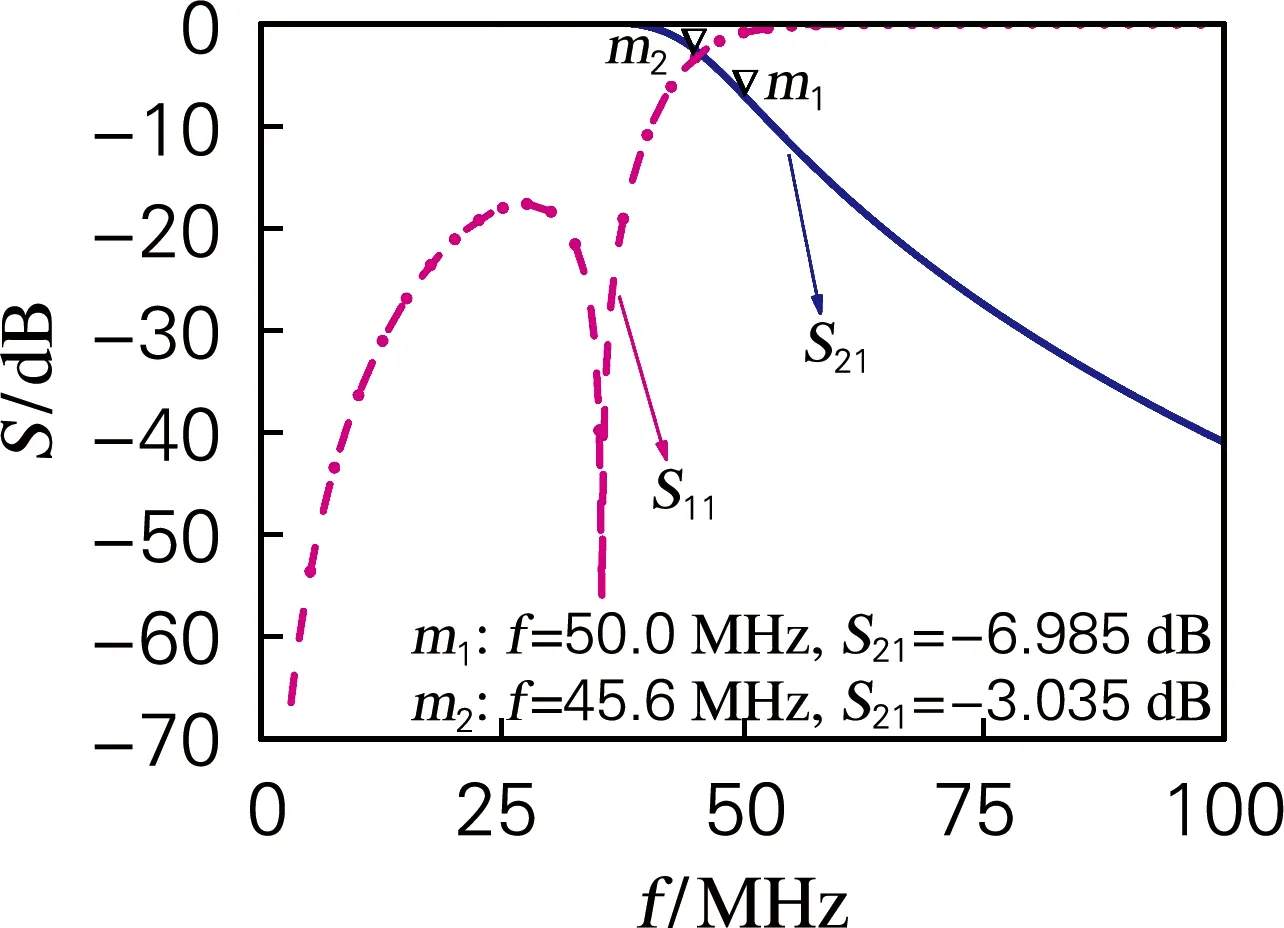
图2 5阶低通滤波器截止特性和反射损耗Fig.2 Cut-off characteristics and reflection loss of 5th order low pass filter

2 基于NSGA-Ⅱ的滤波器优化

2.1 初始种群的产生

随机产生N个个体，作为开始进行迭代运算的初始种群。初始种群数量的规模大小，会影响算法优化后产生结果和运行效率[16]。

在初始种群产生时，初始个体的决策变量通过min(i)+(max(i)-min(i))×rand(1)产生，其中max(i)为个体中决策变量的最大值，min(i)为个体中决策变量的最小值，由于rand(1)为随机值，这就有可能造成初始值相差很小或相等，改进的算法对每个产生的值和其他已产生的值进行相减并取绝对值，如果该绝对值小于(max(i)-min(i))/N，该值就会舍弃，这样就会保证个体密度值的均匀，确保了种群个体的多样性，提高了算法的全局搜索能力。

2.2 适应度函数的确定

采用非负函数的变换，把最小值通过取反加上最大值，变为函数的最大值的形式求取。

(1)

式中：Cmax为f(x)中取值的最大值。

2.3 确定目标函数

将滤波器的插入损耗S21、反射损耗S11和群时延作为优化的目标函数。S21和S11用[ABCD]矩阵表示，可根据式(2)～(4)写出5阶低通滤波器电路的目标函数。

(2)

(3)

(4)

式中：Z0表示滤波器的特征阻抗，H(jω)表示滤波器的传输函数。

2.4 建立约束条件

在NSGA-Ⅱ算法优化过程中对电感、电容的取值约束可以保证优化效率，同时得到最优结果。电感和电容的约束条件如式(5)、式(6)所示。

Cimin≤Ci≤Cimax

(5)

Limin≤Li≤Limax

(6)

式中：i=1，2，…，n，表示不同的元件；Cimin为电容容量的下限；Cimax为电容容量的上限；Limin为电感容量的下限；Limax为电感容量的上限。

2.5 NSGA-Ⅱ算法实现步骤

用NSGA-Ⅱ算法对低通滤波器进行优化，首先设定变量，种群总数为200，优化代数为400，竞争个体数为2，交叉算子为20，变异算子为20。根据约束条件产生初始种群，针对优化目标，通过优化算法从中获得一组最优解，基于最优解x=[C1，L2，C3，L4，C5]，实现该滤波器的优化。NSGA-Ι算法的优化流程如图3所示。

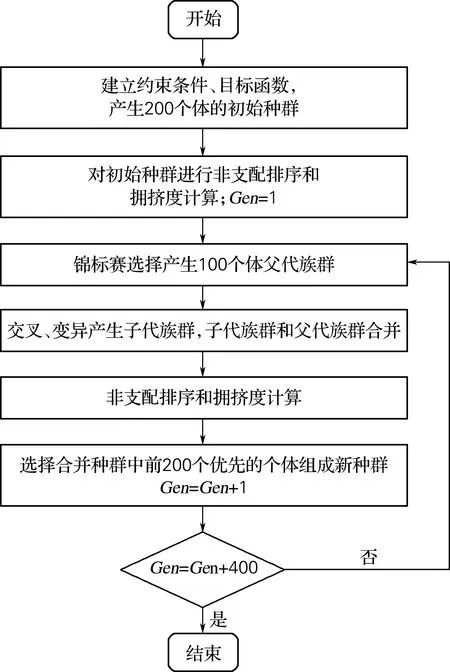
图3 基于NSGA-Ⅱ算法优化流程图Fig.3 Flow diagram of algorithm optimization based on NSGA-Ⅱ

2.6 基于距离值的最优解分析

为了在Pareto解集中找到满足要求的最优解，对解集中的每个解增加了基于距离值分析的功能。距离值是指一个目标函数的任意一个解和设定的优化目标值间的差距。

首先通过式(7)算出解集中插入损耗每个解的距离值D1(N)(N=1，2，…，200)，同理计算出反射损耗、群时延的距离值D2(N)和D3(N)，然后将距离值增加在解集矩阵中。距离值越接近0，该目标解越优。

(7)

式中：T(obji)为目标函数i设定的优化目标值，obji(N)为目标函数i的任意一个解，max(obji)为目标函数i解中的最大值，min(obji)为目标函数i解中的最小值，i=1，2，3。

按照式(8)算出任意一组解中插入损耗、反射损耗、群时延的距离值和，距离值和最小的解为最优解。

(8)

式中：d(N)表示距离值和，Pi为目标函数i的权重，考虑该目标函数，其权重为1，不考虑为0。

3 优化仿真与性能分析

将插入损耗作为优化目标，其他两个目标不做考虑时，此时优先保证插入损耗在50 MHz时是3 dB。用NSGA-Ⅱ算法运算出Pareto解，通过式(7)和(8)找出插入损耗在截止频率50 MHz处插入损耗为3 dB时元器件的值，如表1所示。

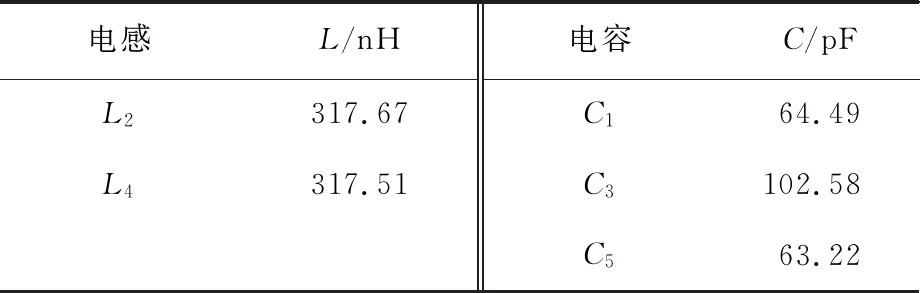
表1 截止频率优化的最优解Tab.1 Optimal solution of cut-off frequency optimization

优化后仿真结果如图4所示，截止频率已经优化至50 MHz，改善了原来低通滤波器截止频率不准确的问题。

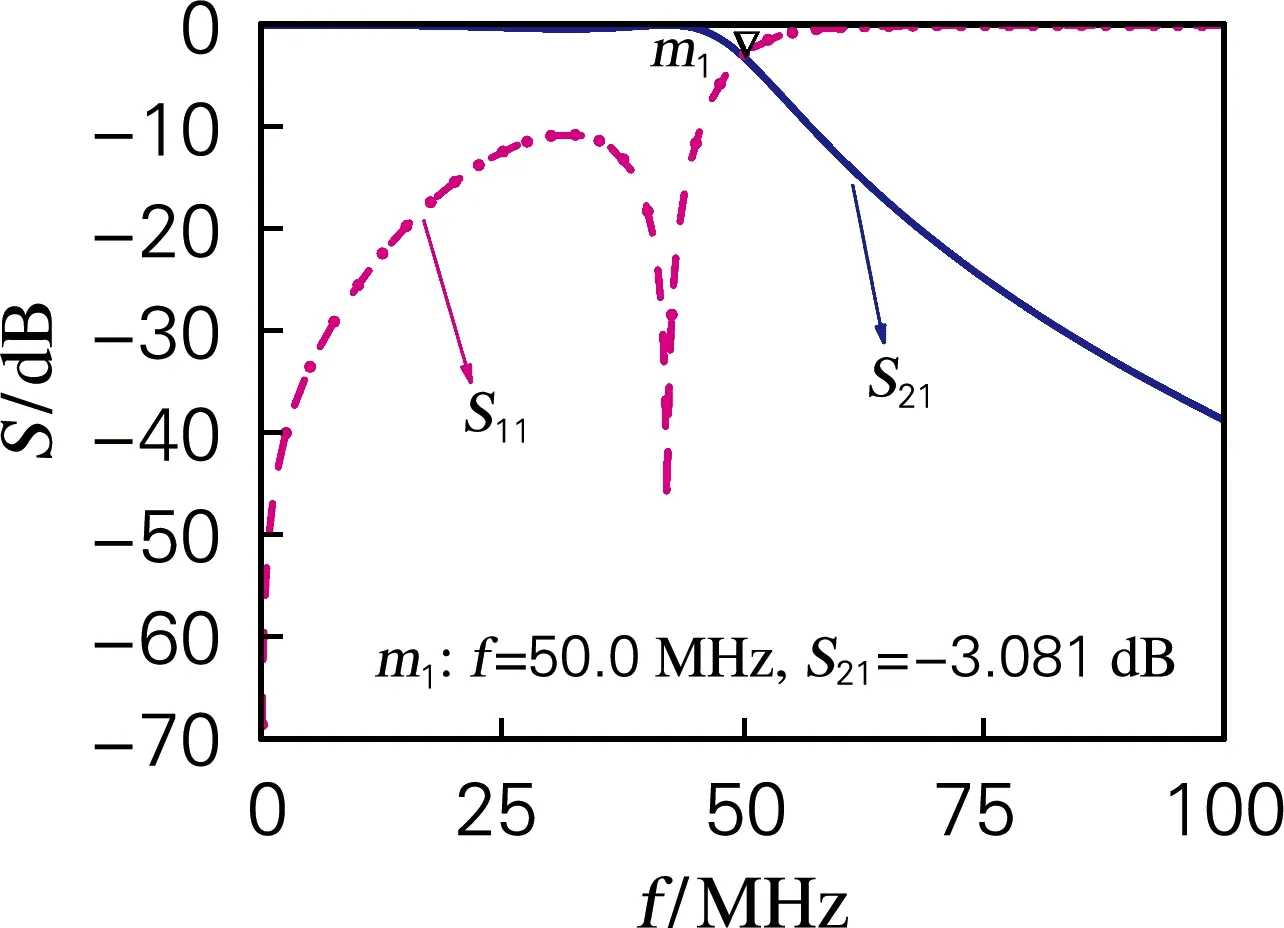
图4 优化截止频率仿真图Fig.4 Simulation of optimized cut-off frequency

将插入损耗、反射损耗和群时延同时作为优化目标。要求在25 MHz时S11≤-15 dB，群时延delay≤1.3 ns，插入损耗尽量靠近50 MHz时3 dB带宽。通过遗传算法运算出该条件下插入损耗、反射损耗和群时延的Pareto解。通过式(7)、(8)在这个解集中运算出最优解，这个解对应的元器件值如表2所示。仿真结果如图5和图6中的S21(opt)、S11(opt)和delay(opt)。插入损耗-3 dB时的截止频率优化到了48.5 MHz，如图7所示。在图7中，考虑插入损耗、反射损耗和群时延，m1所指示的曲线综合指标特性较好，插入损耗特性较为平坦，并且截止频率靠近50 MHz。如果不考虑反射损耗和群时延，截止频率可以优化至规定值。

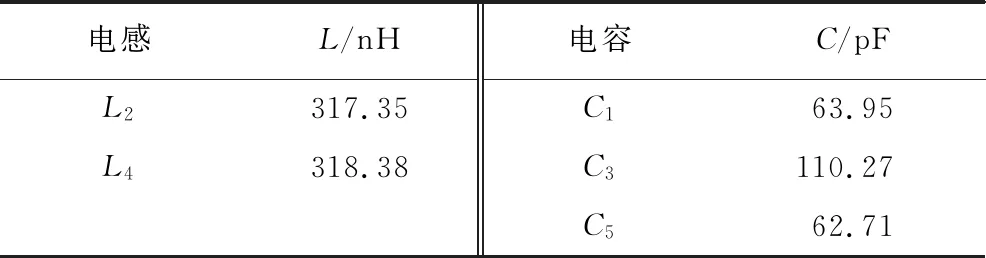
表2 多目标优化的最优解Tab.2 Optimal solution of multi objective optimization

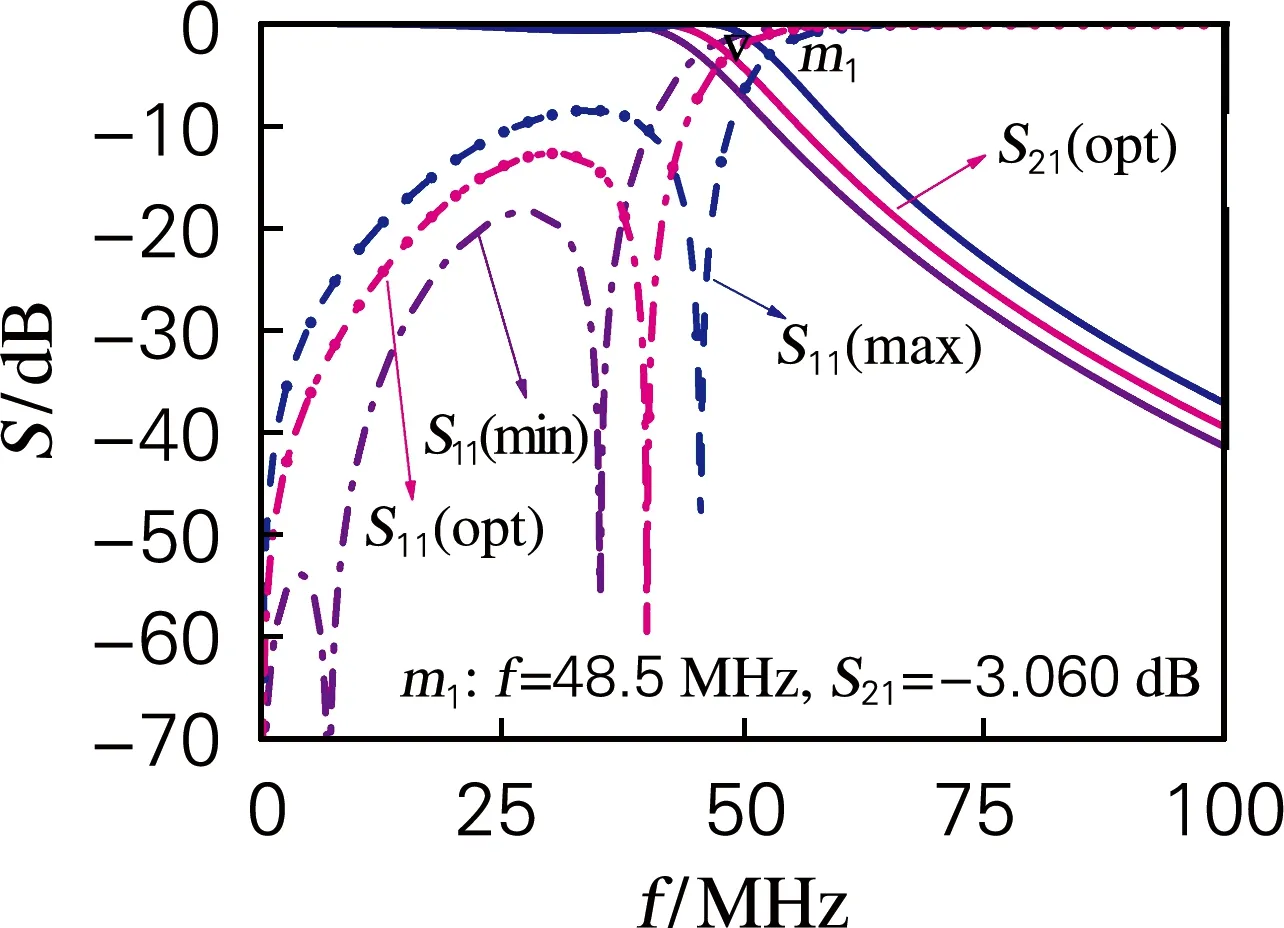
图5 优化反射损耗仿真图Fig.5 Simulation diagram of optimized reflection loss

图6 群时延仿真图Fig.6 Simulation of group delay

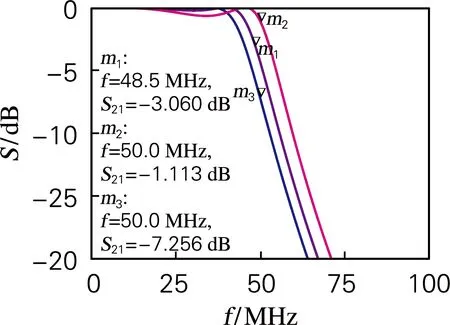
图7 截止频率附近的衰减特性仿真图Fig.7 Simulation of attenuation characteristics near cut-off frequency

4 实际模型仿真与性能分析

在制作滤波器时，需要购置实际器件。电感和电容的理论设计值在实际中并不都存在，需要经过电容和电感的并联和串联实现和理论值大致相等的实际值。优化之前滤波器的理论设计电感值需要3个不同数值的电感串联实现，理论设计电容值需要2个不同的电容并联实现。需要的电感和电容实际值和型号见表3。

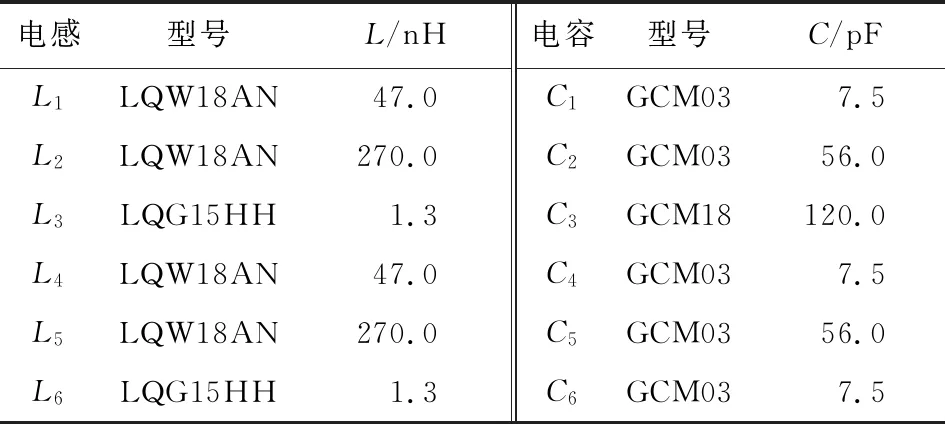
表3 优化前实际电感和电容值Tab.3 Practical inductor and capacitor before optimization

按照表2中优化后的滤波器元器件值制作出实际滤波器模型电路，如图8所示。需要的电感和电容实际值和型号如表4所示。

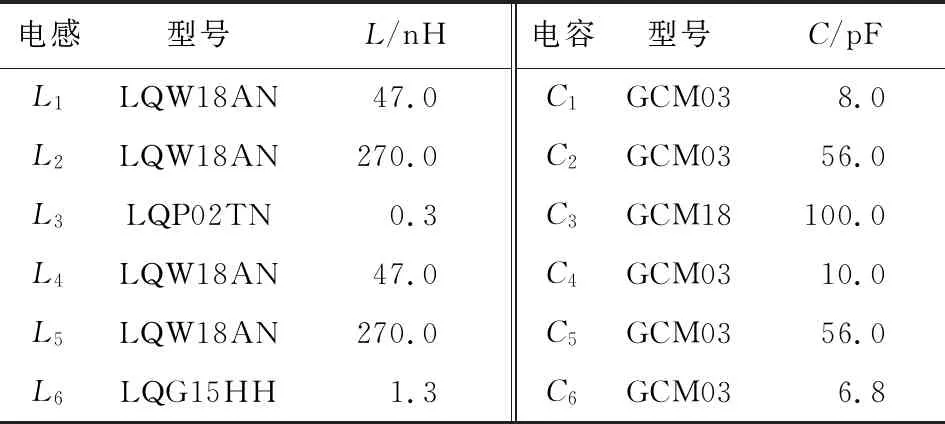
表4 优化后实际电感和电容值Tab.4 Practical inductor and capacitor after optimization

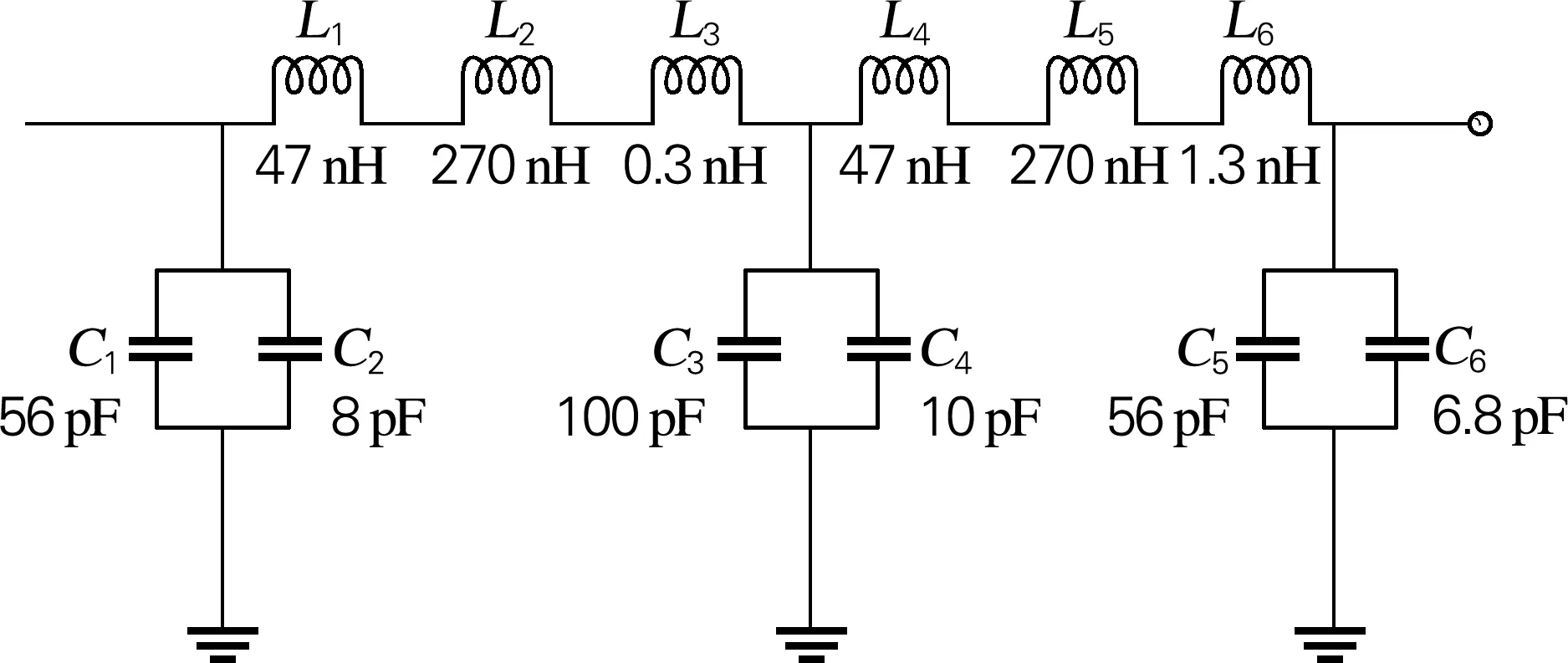
图8 优化后低通滤波器实际电路图Fig.8 Practical circuit of optimized low pass filter

两个实际模型电路的仿真结果如图9所示，由于实际电容和电感存在误差和损耗电阻，所以实际制作出的滤波器插入损耗比理论仿真值增大。但是经过优化后的低通滤波器在50 MHz的插入损耗比优化前的滤波器改善了约2.5 dB。

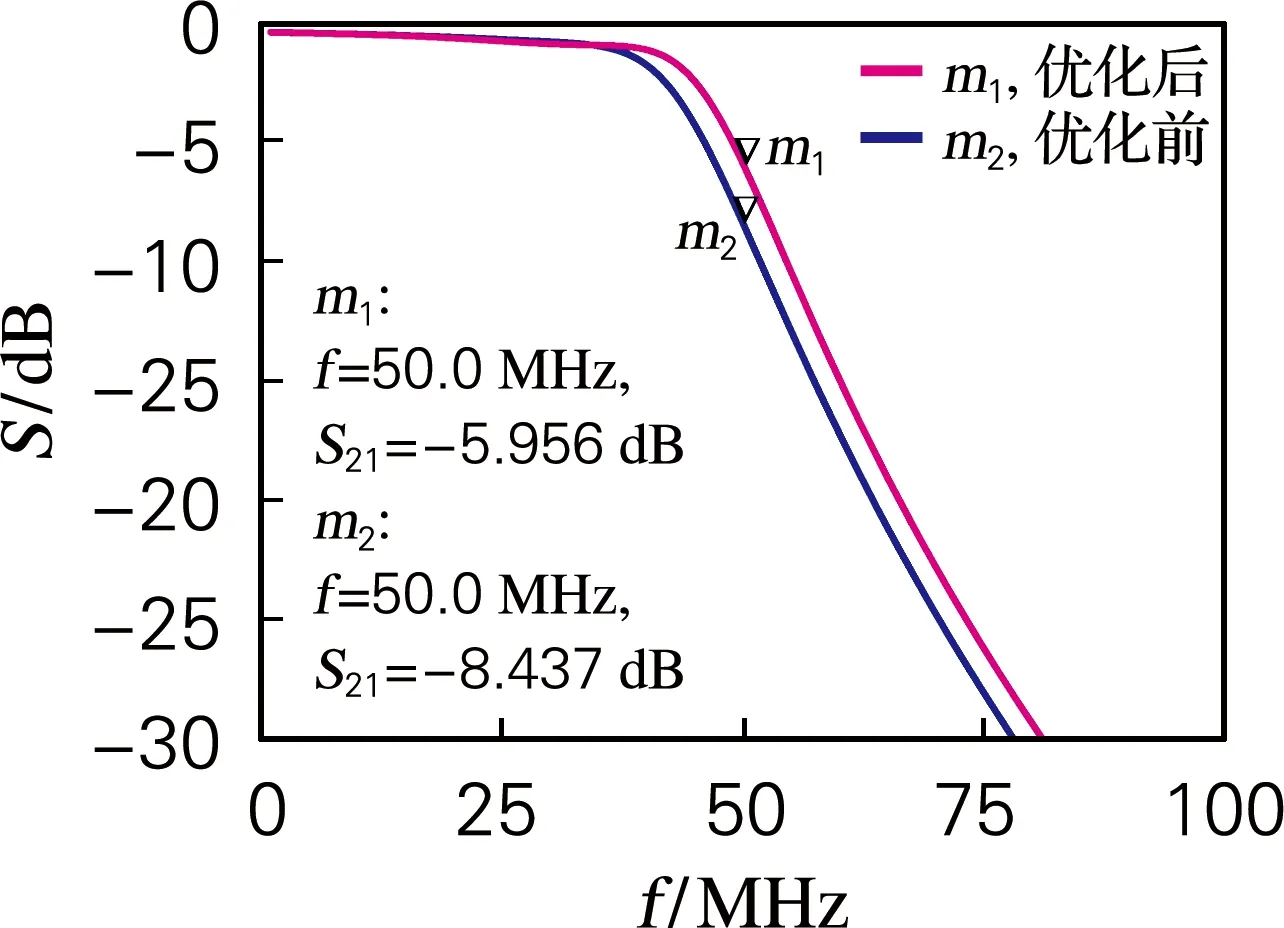
图9 插入损耗比较图Fig.9 Comparison of insertion loss

5 结 论

针对滤波器的插入损耗、反射损耗及群时延等参数相互制约并且运算量大的问题，利用NSGA-Ⅱ优化算法处理多目标问题的优势，将该算法用于低通滤波器性能优化。研究结果表明利用该算法可以将截止频率优化至设计目标，优化后的滤波器实际模型电路比优化前的插入损耗改善了约2.5 dB。研究结果为滤波器实际应用中的性能优化，提供了方法和应用基础。