梯度饱和多孔材料中弹性波的截止频率

周凤玺, 张家齐, 曹小林

(1.兰州理工大学 土木工程学院, 甘肃 兰州 730050;2.西部土木工程防灾减灾教育部工程研究中心, 甘肃 兰州 730050)



梯度饱和多孔材料中弹性波的截止频率

周凤玺1,2, 张家齐1, 曹小林1

(1.兰州理工大学 土木工程学院, 甘肃 兰州 730050;2.西部土木工程防灾减灾教育部工程研究中心, 甘肃 兰州 730050)

基于Biot多孔介质理论,应用WKB(Wentzel-Kramers-Brillouin)法,推导得到SH波和Lamb波在梯度非均匀含液饱和材料中截止频率的解析表达式.求解过程中应用波数趋于零的极限条件,通过简化控制方程,获得平面SH波和P-SV波的截止频率.问题的解答揭示了截止频率与材料的物理力学性质以及非均匀性密切相关.考虑材料参数沿板厚按指数形式变化的饱和多孔板,通过数值算例分析弹性平面波在该类非均质饱和多孔材料中的截止频率变化规律.数值结果表明,截止频率随着板的厚度、孔隙率和非均匀参数及渗透系数的不同均有显著的变化,验证了计算结果满足精确性要求.

功能梯度材料；含液饱和材料；波的传播；WKB法；截止频率

多孔介质材料在岩土工程、地球物理以及生物工程等领域有着广泛的应用,自Biot[1-2]提出描述饱和多孔介质动力特征方程以来,国内外许多专家学者从不同角度对饱和多孔介质中波的传播问题进行研究[3-7],包括多孔介质动力响应问题的解析研究、数值模拟方法以及波的传播特性等的研究.目前关于饱和多孔介质波动问题的研究主要集中在几何特征为无限半空间区域或有限厚度的岩土类材料,而对于多孔饱和材料,特别是非均匀饱和材料中弹性波的截止频率分析研究远落后于对单相连续弹性介质的研究.

20世纪80年代中期,由日本科学家提出了功能梯度材料的概念,国内外许多专家学者从不同角度,包括功能梯度材料的制备[8-9],弹性波在功能梯度材料中的传播特性[10-15]等问题展开了一系列的研究工作,并取得了丰硕的成果.本文以梯度非均匀含液饱和板中弹性波的截止频率为研究内容,基于Biot多孔介质波动模型,考虑到波数趋于零,在该极限条件下,应用WKB方法求解带有变系数的微分方程[16],通过理论推导可以获得非均匀含液饱和板中弹性波截止频率的解析表达式,且表达式满足精确性要求.

1 基本方程

基于Biot多孔介质理论可知,均质饱和多孔介质的基本方程[1-7]如下.

物理方程为

σij=λεkkδij+2μεij-αpδij,

(1)

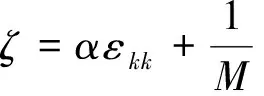
(2)

几何关系为

(3)

运动方程为

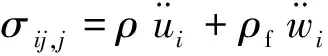
(4)

(5)

考虑饱和材料中的简谐波,则固相位移分量可以表示为

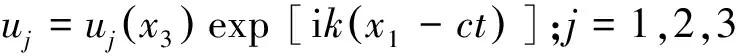
(6)

式中：k为x1方向的波数;c为波速，c=ω/k,其中ω为圆频率.

将式(5)代入式(1)～(4),经过整理可以得到液相位移与固相位移的关系为

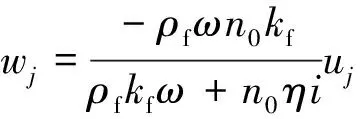
(7)

2 控制方程及通解

2.1 SH波传播的截止频率

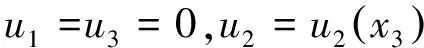
图1 非均匀含液饱和材料Fig.1 Functionally graded fluid-saturated materials

将式(3)和(1)代入式(4),考虑SH波的位移矢量,同时应用波数趋于零的极限条件,可得

(8)

将式(7)代入式(8),可以得到SH波传播的控制方程为

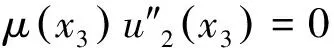
(9)

式中：

采用WKB法求解变系数微分方程(9),设

(10)

且令

(11)

将式(10)及式(11)的前3项代入式(9),经过整理可得

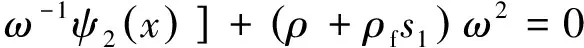
(12)

省略ω-1和ω-2项,并考虑ω2、ω、ω0项前的系数为零,可得

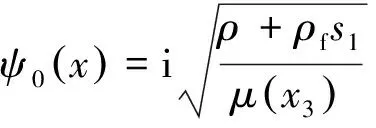
(13)

(14)

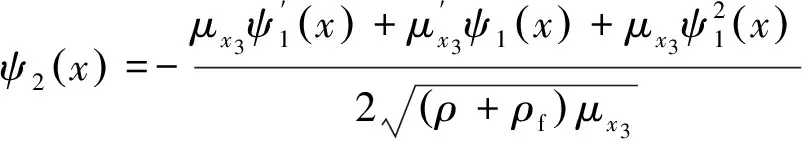
(15)

将式(13)、(14)代入式(10),可得

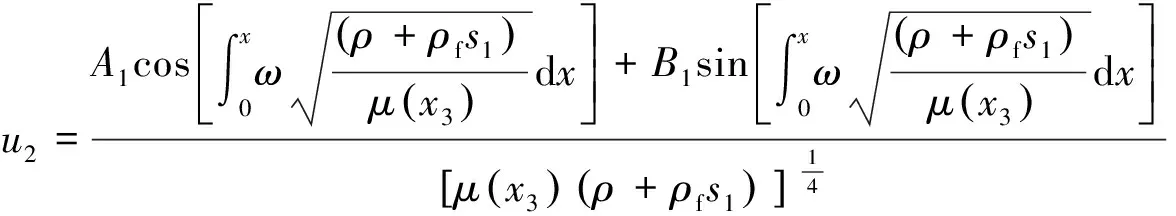
(16)

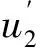
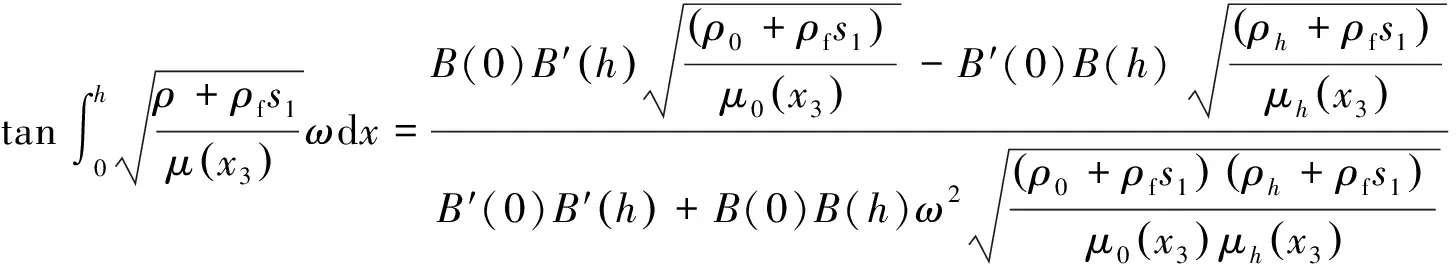
(17)

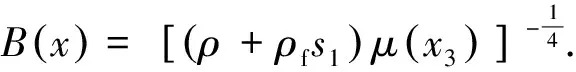
通过求解方程(17),可得SH波的截止频率为

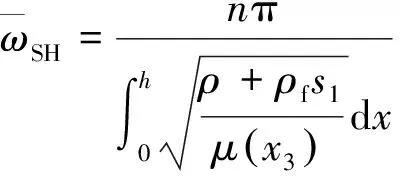
(18)

2.2 Lamb波传播的截止频率

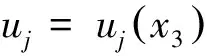
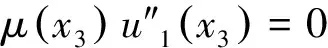
(19)

(20)

(22)

将式(21)、式(22)的前3项分别代入式(19)、(20),计算同SH波的截止频率求解中的式(12),并考虑系数项为零可以得到

(23)

(24)

(25)

(26)

(27)

(28)

式中：

将式(23)、(24)和(26)、 (27)分别代入式(21),可得

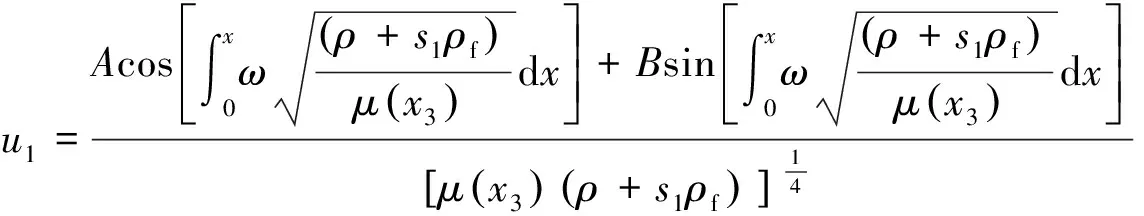
(29)

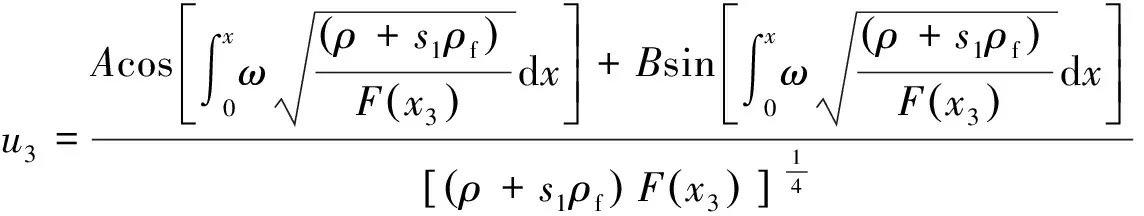
(30)

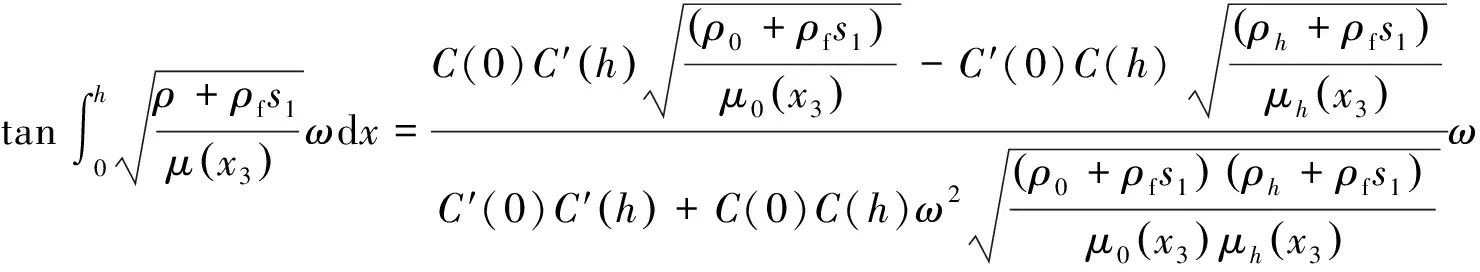
(31)

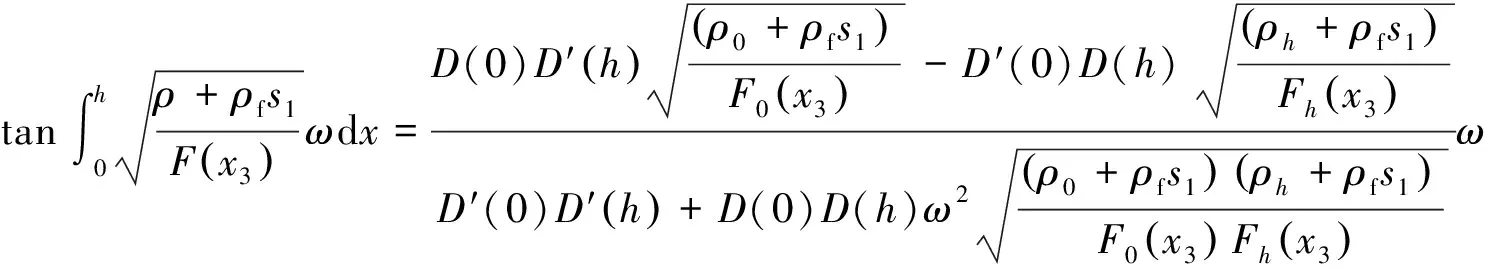
(32)

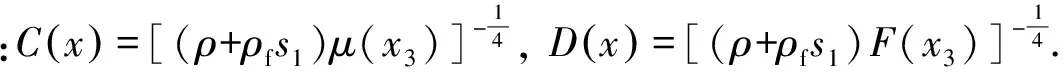
饱和介质中的P波和SV波的截止频率分别为

(33)

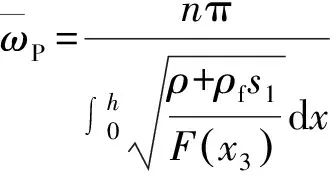
(34)

比较式(33)、(18)可知,饱和介质中SH和SV波的截止频率相同.

3 数值分析与讨论

3.1 精确性验算

WKB的计算结果必须严格满足精确性要求[16],即

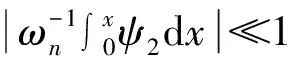
(35)

(36)

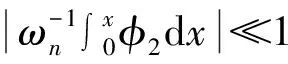
(37)

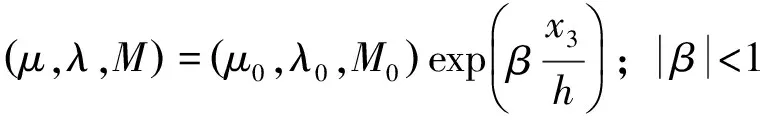
(38)

将式(15)、(25)、(28)分别代入式(35)～(37),可得

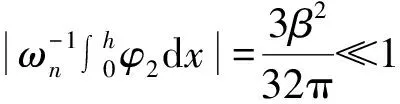
3.2 数值计算

为了对平面弹性波的截止频率进行参数分析,选取多孔饱和介质的材料参数[17]为：λ0=2.0×107kN/m2,μ0=0.6×107kN/m2,α=0.908,M=1.29×107kN/m2,ρf=1 000 kg/m3,ρ=2 458 kg/m3,η=10-3Pa·s.考虑材料力学参数按式(38)沿厚度方向连续变化,对于不同非均匀参数、不同板厚以及不同孔隙率、不同渗透系数下P波以及S波的截止频率ωP、ωS进行分析.

取板厚h=15 cm,渗透系数kf=1.9×10-7m4/(kN·s),孔隙率n0为0.19,图2、3分别给出当非均匀参数β为-0.9～0.9时,S波和P波的前4阶截止频率随非均匀参数的变化曲线.可以看出,当饱和多孔板的厚度、密度、孔隙率、渗透系数一定时,截止频率随着非均匀参数的增加总体呈现近似于线性的增大,截止频率明显受材料非均匀性的影响.有非均匀参数在相同的区间内变化,P波的截止频率明显大于S波的截止频率.

图2 S波截止频率随非均匀参数的变化Fig.2 Relations between gradient coefficient and cut-off frequencies of S wave

图3 P波截止频率随非均匀参数的变化Fig.3 Relations between gradient coefficient and cut-off frequencies of P wave

图4 S波截止频率随板厚的变化Fig.4 Relations between plate thickness and cut-off frequencies of S wave

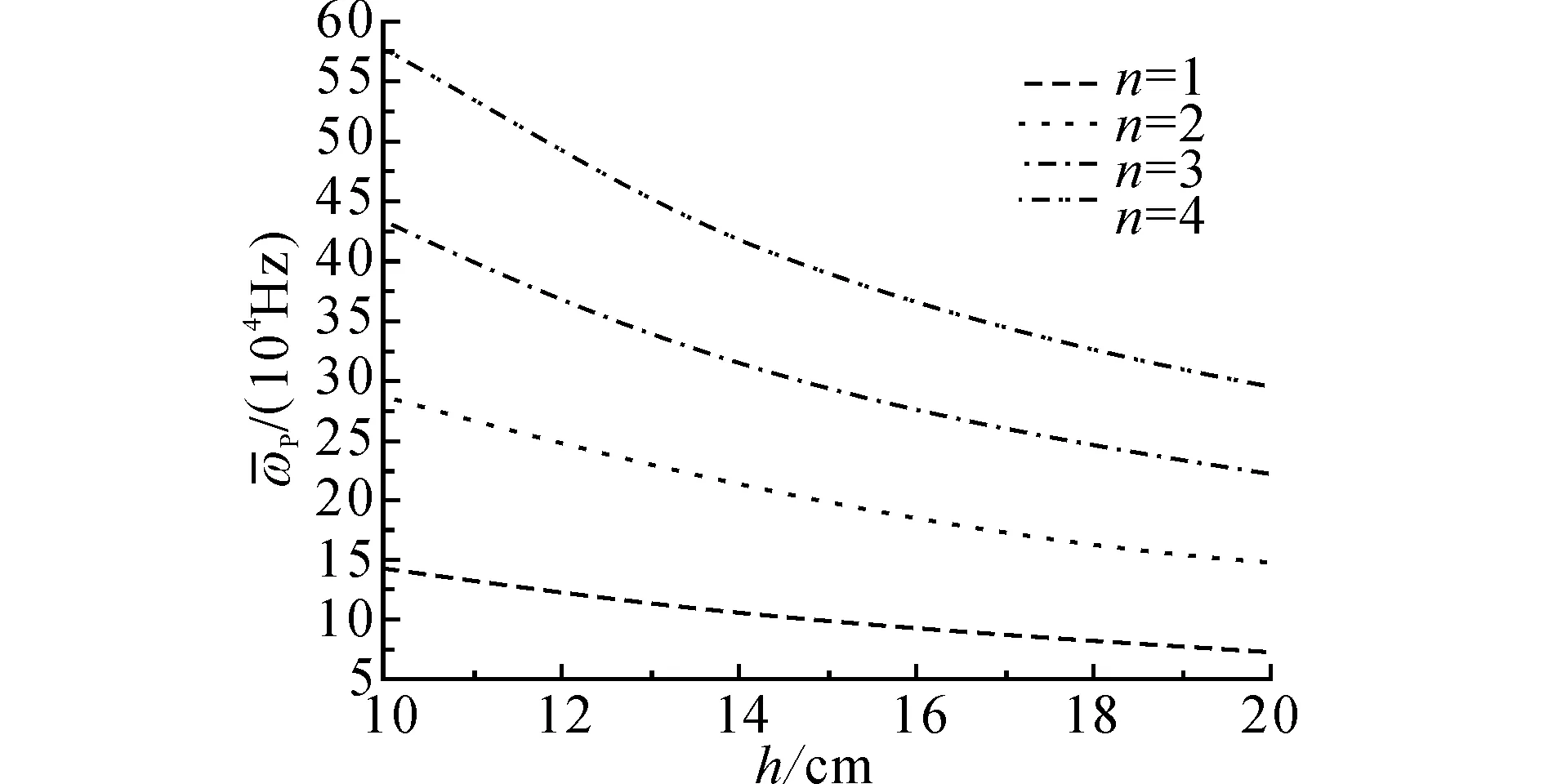
图5 P波截止频率随板厚的变化Fig.5 Relations between thickness and cut-off frequencies of P wave

为了分析板厚对截止频率的影响,在取kf=1.9×10-7m4/(kN·s),n0=0.19,β=0.5的情形下,当板厚h为10～20 cm时,图4、5分别绘出S波和P波的前4阶截止频率随板厚的变化曲线.可以看出,截止频率随着板的厚度增加呈现非线性减小且减小速率越来越小,截止频率明显受材料厚度的影响.

图6 S波截止频率随孔隙率的变化Fig.6 Relations between porosity and cut-off frequencies of S wave

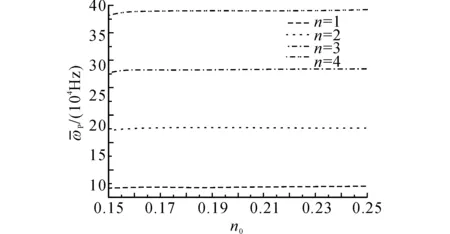
图7 P波截止频率随孔隙率的变化Fig.7 Relations between porosity and cut off frequencies of P wave

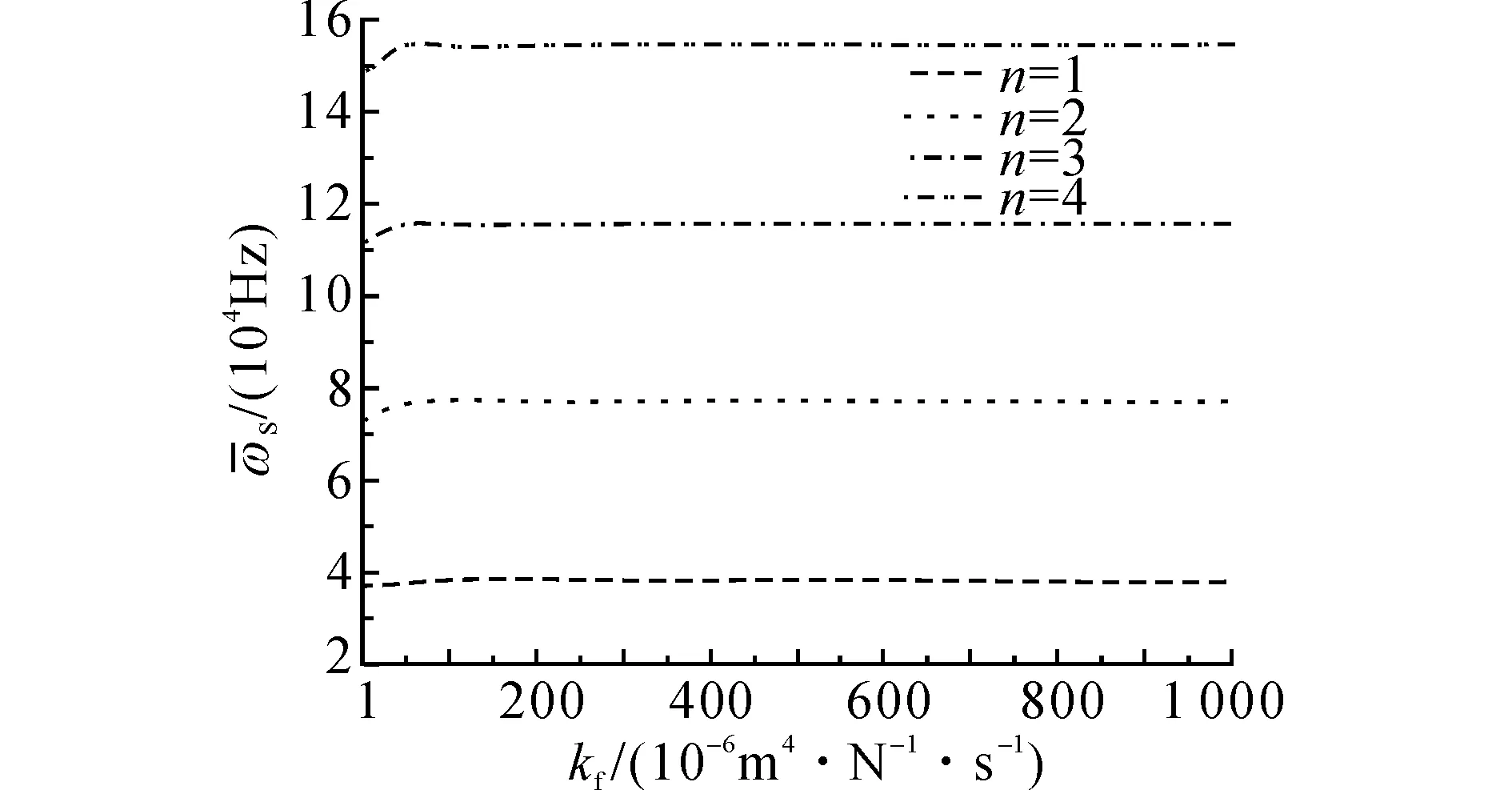
图8 渗透系数和S波截止频率之间的关系Fig.8 Relations between permeability and cut-off frequencies of S waves

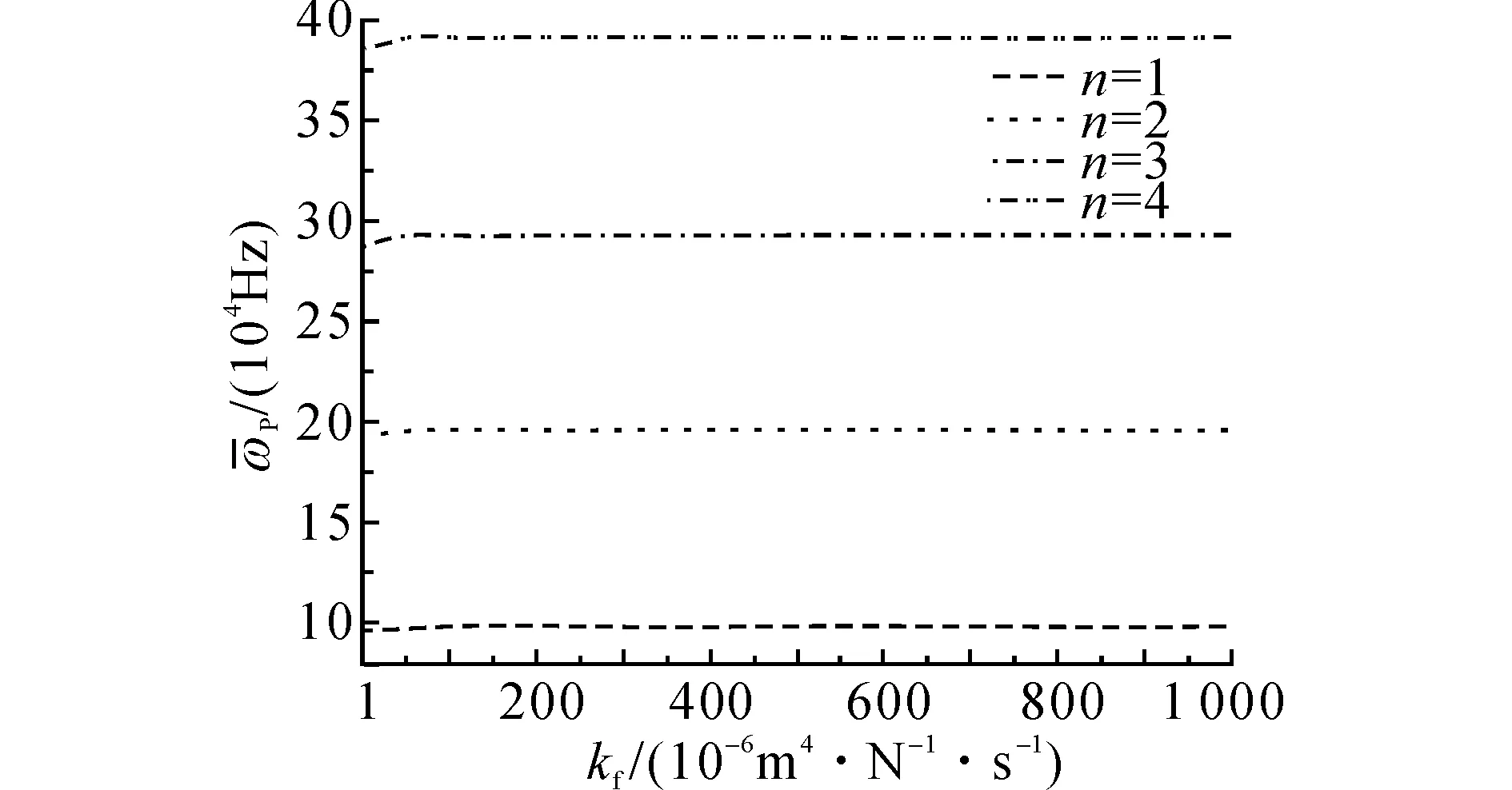
图9 渗透系数和P波截止频率之间的关系Fig.9 Relations between permeability and cut-off frequencies of P waves

如图6、7所示为当h=15 cm,β=0.5,n0为0.15～0.25时,S波和P波截止频率的变化.可以看出,当孔隙率较小时,截止频率随孔隙率的增加明显增大,而随着孔隙率的进一步增加,两类波的截止频率均变化不大.取h=15 cm,β=0.5,图8、9分别给出当kf为10-6～10-3m4/(kN·s)时S波和P波的截止频率.由图8、9可以看出,当渗透系数较小时,截止频率随渗透系数的增大而明显增大；当渗透系数大到一定程度后,S波和P波的截止频率随渗透系数的变化不是很大.

4 结 语

基于Biot多孔介质理论,通过理论分析获得SH和Lamb波在梯度非均匀含液饱和板中传播的截止频率.考虑材料密度为常数,模量沿板厚方向按指数形式连续变化的情形,通过数值算例参数分析各影响因素对横波以及纵波截止频率的影响规律.数值结果表明：在相同条件下,P波的截止频率总大于S波的截止频率；材料的非均匀性和板的厚度以及材料的密度对截止频率的影响较大,孔隙率和渗透系数对截止频率的影响相对小；弹性波的截止频率随板厚度的增大而减小,随多孔介质中孔隙率增大呈增大趋势,并且截止频率随非均匀参数及渗透系数的增大而增大.

[1] BIOT M A. Theory of elastic waves in a fluid-saturated porous solid, I. low frequency range [J]. The Journal of Acoustical Society of America, 1956, 28(2)： 168-178.

[2] BIOT M A. Theory of elastic waves in a fluid-saturated porous solid, II. high frequency range [J]. The Journal of Acoustical Society of America, 1956, 28(2)： 179-191.

[3] 柯燎亮, 汪越胜, 章梓茂. 非均匀土中Love波的传播特[J]. 岩土力学, 2004, 25(增刊): 369-374. KE Liao-liang, WANG Yue-sheng, ZHANG Zi-mao. Properties of love waves in inhomogeneous saturated soil [J]. Rock and Soil Mechanics, 2004, 25(supplement): 369-374.

[4] 邵秀民,蓝志凌.流体饱和多孔介质波动方程的有限元解法[J].地球物理学报, 2000, 43(02): 264-278. SHAO Xiu-min, LAN Zhi-ling. Finite element methods for the equations of waves in fluid-saturated porous media [J]. Chinese Journal of Geophysics, 2000,43(02): 264-278.

[5] 李伟华,赵成刚.平面SV波在饱和土半空间中圆柱形孔洞周边的散射[J].地震工程与工程振动, 2008, 28(6): 2-7. LI Wei-hua, ZHAO Cheng-gang. An analytical solution for the scattering of plane SV-waves around cylindrical cavity in a fluid-saturated porous-media half space [J]. Journal of Earthquake Engineering Vibration, 2008,28(6): 2-7.

[6] 周凤玺,赖远明.条形荷载作用下梯度饱和土的动力响应分析[J].岩土力学, 2013, 34(6): 1724-1730. ZHOU Feng-xi, LAI Yuan-ming. Dynamic responseanalysis of graded fluid-saturated soil under strip load [J]. Rock and Soil Mechanics, 2013, 34(6): 1724-1730.[7] ZHOU F, LAI Y, SONG R. Propagation of plane wave in non-homogeneously saturated soils [J]. Science China Technological Sciences, 2013, 56(2): 430-440.

[8] LIANG L, MENG Q, CHEN S, et al. Synthesis of TiB2-TiC-Ni/TiAl/Ti functionally gradient materials by FAPAS process [J]. Rare Metals, 2011, 30(supple.1): 467-471.

[9] RAJAN T P D, PILLAI R M, PAI B C. Functionally graded Al-Al3Ni in situ intermetallic composites: fabrication and microstructural characterization [J]. Journal of Alloys and Compounds, 2008, 453(1): L4-L7.

[10] 曹小杉,金峰,王子昆.功能梯度材料板中Lamb波传播特性研究[J].固体力学学报, 2009, 30(2): 35-41. CAO Xiao-shan, JIN Feng, WANG Zi-kun. Propagation properties of Lamb waves in a functionally graded material plate [J]. Chinese Journal of Solid Mechanics, 2009, 30(2): 35-41.

[11] GAO L, JI W, ZHENG Z, et al. An analysis of surface acoustic wave propagation in a plate of functionally graded materials with a layered model [J]. Science in China Series G: Physics, Mechanics and Astronomy, 2008, 51(2): 165-175.

[12] GAO L, WANG J, ZHONG Z, et al. An exact analysis of surface acoustic waves in a plate of functionally graded materials [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009,56(12): 2693-2700.

[13] 刘睫,王子昆,张陵.梯度材料层状结构中的love波[J].固体力学学报, 2004, 25(2): 165-170. LIU Jie, WANG Zi-kun, ZHANG Ling. Love waves in layered structures with graded materials [J]. Acta Mechanic Solida Sinica, 2004, 25(2): 165-170.

[14] ALLAHVERDIZADEH A, OFTADEH R, MAHJOOB M J, et al. Homotopy perturbation solution and periodicity analysis of nonlinear vibration of thin rectangular functionally graded plates [J]. Acta Mechanica Solida Sinica, 2014, 27(2): 210-220.

[15] CAO X, JIN F, JEON I. Characterization of the variation of the material properties in a freestanding inhomogeneous thin film [J]. Science Direct Physics Letter, 2010, 375(2): 220-224.

[16] CAO X, SHI J, JIN F. Wentzel-Kramers-Brillouinsolution of cut-off frequency for horizontal shear (SH) waves in various inhomogeneous thin films [J]. Philosophical Magazine Letters, 2012, 93(1): 34-41.

[17] NAGLER L, SCHANZ M. An extendable poroelastic plate formulation in dynamics [J]. Archive of Applied Mechanics, 2010, 80(10): 1177-1195.

Analysis of cut-off frequencies for functionally graded fluid-saturated materials

ZHOU Feng-xi1,2, ZHANG Jia-qi1, CAO Xiao-lin1

(1.DepartmentofGeotechnicalEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China;2.TheWesternCivilEngineeringDisasterPreventionandMitigationEngineeringResearchCenteroftheMinistryofEducation,Lanzhou730050,China)

The analytical expression for the cut-off frequencies of the horizontal shear waves (SH wave) and Lamb waves (P-SV wave) in a functionally graded inhomogeneous fluid-saturated media was deduced by applying the WKB (Wentzel-Kramers-Brillouin) method based on Biot’s theory of poroelastic medium. In the process of solving, the cut-off frequencies of SH wave and P-SV wave were obtained with the limiting condition of the wave number approaching zero by simplifying the governing equation. The solution to the problem revealed that the cut-off frequencies were closely associated with the physico-mechanical properties and the heterogeneity of the material. The material parameter of the fluid-saturated poroelastic plate changing along the thickness direction as an exponential form was considered. The changing regularity of the elastic plane wave’s cut-off frequencies in the inhomogeneous fluid-saturated porous plate was analyzed by numerical examples. The numerical results showed that the cut-off frequencies were related to the material properties of the fluid-saturated material, including thickness of the plate, porosity, gradient index and permeability. The accuracy of the numerical solution was validated.

functionally graded materials; fluid-saturated poroelastic plate; propagation of wave; Wentzel-Kramers-Brillouin method; cut-off frequency

2015-01-10. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

国家自然科学基金资助项目(51368038,11162008)；甘肃省环保厅科研资助项目(GSEP-2014-23)；甘肃省教育厅研究生导师基金资助项目(1103-07).

周凤玺(1979—),男,教授,从事岩土力学和非均匀材料结构力学的研究.ORCID; 0000-0003-4709-2419. E-mail: geolut@163.com

10.3785/j.issn.1008-973X.2016.04.020

O 343

A

1008-973X(2016)04-0744-06