基于超声Lamb波截止频率的双层薄板各层厚度表征

潘 蕾，沈中华，刘祥恩，阚威威

(南京理工大学 理学院，南京 210094)

双层板状材料具有刚度大、冲击性能好、成本低等优点，在建筑、汽车制造、航空航天、压力容器制造及镀膜等行业都有非常广泛的应用，如表面带涂层的涡轮叶片、飞机多层黏合材料或搭接材料等。板状材料的厚度是该结构的重要参数，因此对其厚度进行表征尤为重要。

超声波测量方法具有对被测结构要求低、空间分辨率高、受测试环境影响小、对人体无害等优点，广泛用于物体厚度的测量。目前，常用的超声波测量方法有脉冲回波法、表面波法和Lamb波法。脉冲回波法通过测量超声脉冲在样品中的传播时间，然后根据传播速度求得样品厚度。但该法通常会在测量的样品厚度为波长量级时达到极限，被测样品上、下表面、交界面处的反射回波混叠在一起，导致无法计算层厚[1-2]。黄巧盛等[3]针对三层结构测量中的回波混叠问题，采用RLS自适应滤波算法处理提取下界面回波信号，成功测量了0.15，0.17，0.19，0.21 mm等4种硅橡胶层的厚度，最大误差为3.5%。KRUGER等[4]通过在TiN膜表面处激发出表面波，测量薄膜的厚度，测量误差为3%。XIAO等[5]通过研究薄膜厚度对声表面波频散现象的影响，提出了一种基于理论和试验色散曲线的厚度计算方法，测得SiO2膜厚度的相对误差最大为2.18%，但该方法只适用于测量层厚较厚(大于波长量级)的双层结构；对于两层都很薄的双层板，可采用Lamb波法，Lamb波法通常利用Lamb波在频域上产生的尖锐明显的共振峰信号来测量厚度[6-7]。GRUENSTEIDL等[8]提出了一种利用零群速度Lamb波同时确定各向同性板厚度及纵向和剪切弹性波速度的方法，厚度测量误差为1.7%。CHO等[9]将其应用于多层结构中几十毫米厚的中间层厚度测量，各模态零群速度频率随连接层厚度增加而单调下降，对厚度的测量误差在微米量级。Lamb波群速度共振法虽能很好地对双层薄板进行测量，但在试验中不易观察到明显的共振现象。

因此，需要一种当双层薄板各层厚度在波长量级甚至小于波长时，也能够很好地测量各层厚度的方法以解决上述问题。笔者提出了一种基于超声Lamb波截止频率测量双层薄板各层厚度的方法，理论推导了双层薄板Lamb波截止频率与两板厚度比的关系。以双层薄板(非铝/铝)为研究对象，理论计算了不同厚度比的双层薄板Lamb波A1模态截止频率，得到A1模态截止频率随厚度比变化的曲线，并分析了非铝板横波速度对其变化的影响。

1 双层薄板Lamb波截止频率的理论研究

Lamb波是一种板波，横波分量和纵波分量在双层板状材料中传播时，在上下边界和交界面处会发生反射，且纵波与横波间会发生模式转换，形成Lamb波[10-11]。Lamb波具有衰减小、传播距离远、信号强、多模态等特点，广泛应用于薄板材料的无损检测与缺陷评估中。

为了简化分析，假定双层薄板各层都是各向同性的，薄板在x和y方向上无限均匀延伸，在z方向上有限，交界面与两自由表面平行，双层板的几何描述如图1所示。其中两板的纵波速度为cLi；横波速度为cTi；厚度为hi；密度为ρi，i(i=1，2)表示层数；d为两板总厚度。

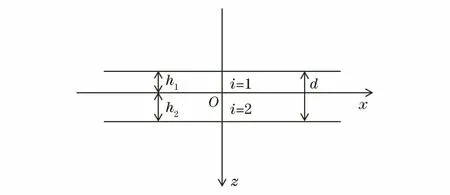
图1 双层板的几何描述示意

通常采用Helmholtz分解法求解运动方程[12]，每一层得到两个独立的波动方程，即

(1)

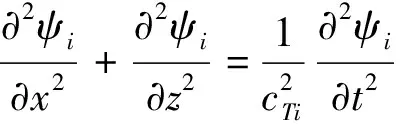
(2)

式中：φi为纵波；ψi为横波势函数。

φi=[AiLcos(piz)+BiLsin(piz)]exp[i(kx-ωt)]

(3)

ψi=[AiTcos(qiz)+BiTsin(qiz)]exp[i(kx-ωt)]

(4)

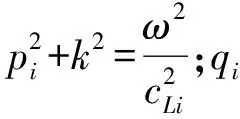
切向位移ux和法向位移uz满足

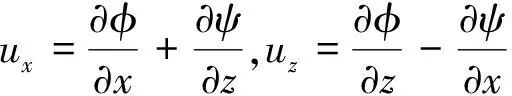
(5)

切向应力σxz和法向应力σzz满足

(6)

式中：λ和μ为拉梅常数。

在两板的自由表面处(z=-h2和z=h1)应力都为零；在交界面处(z=0)，位移和应力连续。所有表达式略去exp[i(kx-ωt)]项，方程组有非平凡解则令系数矩阵行列式为零，得到波数k和频率f的关系。

厚度共振响应表现为k=0，f≠0的点处，此时频率f为截止频率，表示为fc，代入到值为零的行列式中，得到

(7)

当固定双层薄板总厚度和其中一层材料参数时，Lamb波截止频率与两板厚度比和另一层材料的性质有关，分析时用横波速度来描述材料性质。下面以总厚度1 mm的双层薄板(非铝/铝)为研究对象，计算不同厚度比的双层薄板Lamb波A1模态截止频率，得到A1模态截止频率随厚度比变化的曲线，分析非铝板横波速度对其变化的影响。

2 双层薄板Lamb波截止频率的计算

对双层薄板Lamb波截止频率进行理论计算，计算时固定薄板总厚度为1 mm，第一层材料为铝，改变第二层材料和两板厚度比，厚度比r为铝板厚度与非铝板厚度的比值。为了系统地研究不同材料性质对双层薄板Lamb波截止频率的影响，设定m为非铝板横波速度与铝板横波速度的比值。笔者分别选取横波速度比铝的横波速度小很多(0.2≤m≤0.6)、相对接近(0.6

表1 理论计算时使用的材料及其物理参数

以表1中材料组成的非铝/铝双层薄板为研究对象，其总厚度为1 mm，改变两板厚度比r，r的变化范围为[1/9，9]。研究时取Lamb波A1模态截止频率，计算不同厚度比对应的截止频率，作出其随厚度比变化的曲线，根据变化规律将m分成4种情况：0.2≤m≤0.6；0.6

由图2可见，当厚度比趋近于9时， A1模态截止频率逐渐趋近于1 mm铝单板A1模态截止频率；当厚度比趋近于1/9时，截止频率逐渐趋近于1 mm非铝单板A1模态截止频率。

图2 m不同时双层薄板Lamb波A1模态截止频率随厚度比的变化曲线

如图2(a)所示，当0.2≤m≤0.6时，非铝板与铝材料性质差别很大。双层薄板Lamb波A1模态截止频率随厚度比单调递增或除某一段区间内出现截止频率平台外单调递增。可以清晰地看出铅/铝双层薄板Lamb波A1模态截止频率在[1/9，9]内单调递增，截止频率与厚度比一一对应，当试验测得A1模态截止频率时，可以在曲线上找到唯一的厚度比，从而求出薄板各层厚度；而金/铝和银/铝双层薄板A1模态截止频率分别在r为2.4和1.9时出现略微下降，后趋于平缓，截止频率分别在1.08 MHz和1.18 MHz左右出现平台，也就是说当测得截止频率在这两个值附近时，无法区分厚度比，测量误差较大，而在其他频率处测量薄层厚度是可行的。

如图2(b)所示，当0.6

如图2(c)所示，当0.9≤m≤1.1时，即非铝板与铝材料性质相近，双层薄板Lamb波A1模态截止频率同样随厚度比先增加后降低再增加，但与上一种情况不同的是，截止频率会超出1 mm铝单板A1模态截止频率与1 mm非铝单板A1模态截止频率的范围。同样地，在该区间内需要更高阶截止频率来确定唯一的厚度比。

如图2(d)所示，当m很大(m=1.99)时，曲线趋势与m在1附近时类似。由于m很大，氮化硅与铝材料性质差别很大，1 mm氮化硅板A1模态截止频率是1 mm铝板的m倍，相差很大。曲线上两个峰值频率对应的厚度比在计算区间的两个端点附近，所以氮化硅/铝双层薄板Lamb波A1模态截止频率在大的厚度比区间[1/9，7]内单调递减，非常适合测双层薄板各层厚度；当r大于7时，截止频率开始缓慢递增，在1.54 MHz处出现平台，导致在[7，9]区间内无法区分厚度比，又由于该区间厚度比都很大，试验测量时并不会出现较大误差。

3 结语

笔者利用Lamb波A1模态在截止频率处产生的厚度共振，对双层薄板各层厚度进行表征，理论推导出了双层薄板截止频率与两板厚度比之间的关系。理论计算时以总厚度1 mm的非铝/铝双层薄板为研究对象，计算不同厚度比的双层薄板Lamb波A1模态截止频率，得到了截止频率随厚度比变化的曲线，发现非铝板横波速度对变化曲线有着重要的影响。当两种材料横波速度相差很大时，用Lamb波A1模态截止频率测量厚度是可行的；当横波速度相差相对较小时，则需要更高阶截止频率来确定唯一的厚度比，来得到双层薄板各层厚度。

笔者通过双层薄板Lamb波厚度共振的激发探测试验验证了该方法的可行性，试验结果表明，当截止频率随厚度曲线上同一截止频率对应多个厚度比时，需要求得更高阶截止频率与厚度比的变化曲线，并排除不期望的厚度比。