圆锥曲线中的“小垂直,大确定”——由2020年天一联考第22题引发的探究

广东省珠海市斗门区第一中学(519100) 刘晓玉 邢维金

解析几何中常常出现的定点、定值、定位、定圆、定线等问题,是各省数学试题的命题热点,也是高考的一大难点.此类问题动中有定,定中有动,并且常与轨迹问题、曲线系问题等相结合,深入考查直线与圆锥曲线的综合应用.它不但考查学生掌握知识的水平,更注重考查学生灵活运用知识的能力和解题方法的创新.笔者试图通过对天一大联考第22 题的深入探究,力求以一题多解,一题多变的方式深挖试题的本质,以达到以一通百的效果.

一、试题呈现,考点分析

题目(2021 届天一大联考第22 题) 过椭圆C1:的右顶点作直线交抛物线C2:y2= 4x于A,B两点,M为AB的中点,O为坐标原点.

(1)求证:|OM|=

(2)设射线OA,OB分别与椭圆C1相交于D,E两点,作ON⊥DE,垂足为N,点F为抛物线的焦点,求|NF|的最小值.

分析试题看起来中规中矩,实则内涵深刻,大道至简,从知识层面看以考查椭圆与抛物线的几何性质、直线与圆锥曲线的位置关系为载体,最值问题为落脚点;从能力层面看主要考查学生推理论证能力和转换运算能力,综合检测学生的探究能力和创新能力,能很好的激发学生的数学潜能.

二、解法赏析,思维碰撞

解析(1)由条件得椭圆C1的右顶点为(4,0),设直线AB的方程为x=my+4,与y2= 4x的联立,消去x得y2−4my −16 = 0.设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=−16,x1x2+y1y2=(my1+4)(my2+4)+y1y2=(1+m2)y1y2+4m(y1+y2)+16=0.所以OA⊥OB.

(2) 解法一(设而不求,整体消参) 设直线DE的方程为x=ty+n,与= 1 联立,消去x得(t2+4)y2+2tny+n2−16 = 0.设D(x3,y3),E(x4,y4),则y3+y4=从而x3x4=(ty3+n)(ty4+n)=

由(1) 知OD⊥OE,所以x3x4+y3y4= 0,整理得5n2=16(t2+1).所以|ON|=又由条件可得F(1,0),所以|OF|= 1,所以|NF|≤|ON|−|OF|=−1,(当且仅当O,F,N三点共线时等号成立),所以|NF|min=

评注本解法是学生较为常用的做法,设而不求,设参消参,最终发现是定值,再利用三点共线时取得最值解决问题.

解法二(巧用轨迹,几何求最) 前面同解法一解得|ON|=所以N点的轨迹为点F在圆内,所以|NF|min=r −|OF|=

评注本解法是顺着解法一中的结论|ON|是定值,从而得点N的轨迹是定圆,然后转化为圆外一点与圆上一点的最小距离问题.

解法三(先猜后证,简化计算)由于点O,F已知,点N为动点,|NF|≤||ON|−|OF||,(当且仅当O,F,N三点共线时等号成立),所以此时点N在x轴上.又ON⊥DE,所以DE垂直与x轴,又由(1)知,OD⊥OE,所以∆ODE为等腰直角三角形.即直线OD的方程为y=x,与联立,解得xD=所以xN=xD=所以|NF|min=||ON|−|OF||=−1.验证,此时直线AB得方程为x=4,过右顶点为(4,0),符合题意.

评注本解法由特殊情况入手,直接抓住问题本质,利用几何性质,化繁为简,避开了解析几何中繁杂的计算问题,提高解题效率.

以上三种解法从探究|ON|为定值,点N轨迹为定圆,以及点N取特值时的定位,三个不同角度出发思考问题,各显神通,充分体现了试题考查的灵活性与创新性.为考生的思维方式多元化提供了较大的发挥空间.

三、结论推广,揭示本质

在上述一题多解过程中,笔者发现本题可以从很多角度进行考查,题目中由原点出发的两个半弦互相垂直时,我们可以得到一些定值、定轨迹等结论,下面将一般情况整理如下:

结论1椭圆= 1 上任意两点A,B,O为坐标原点,且OA⊥OB.

(1)点O到直线AB的距离为定值

(2)若存在点N,ON⊥AB,且垂足为N,则点N的轨迹为定圆x2+y2=

证明(1) 当直线AB斜率不存在时,由于OA⊥OB,(不妨设点A在第一象限,其他情况同理) 根据椭圆的对称性可知,联立

解得xA=所以点O到AB的距离为当直线AB斜率存在时,设y=kx+t联立消去y得(a2k2+b2)x2+2a2ktx+a2(t2−b2)=0.

设A(x1,y1),B(x2,y2),由韦达定理,则x1+x2=,y1y2=(kx1+t)(kx2+t)=因为x1x2+y1y2= 0.所以化简得|t|=故O到AB的距离为

综上,O到AB的距离为定值

由(1)即可推出(2)(3).

(4) 当OA斜率不存在时,则|OA|=b,|OB|=a,易证当OA斜率存在时,联立

消去y得(a2k2+b2)x2−a2b2= 0,解得所以OA2=(1+k2)同理

所以

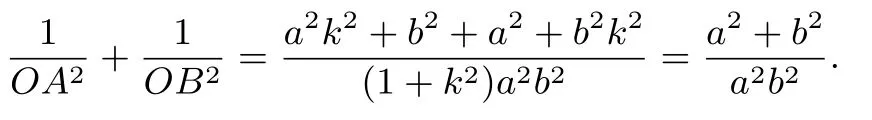
由于椭圆与双曲线有着诸多相似的几何性质,所以笔者尝试将上述结论类比到双曲线中:

结论2双曲线= 1(b > a)上任意两点A,B,O为坐标原点,且OA⊥OB.

(1)点O到AB的距离为定值

通过论证,得到以上两个定值结论.

四、学以致用,理论提升

例1(2019 湖北华中师范大学附中模拟考第20 题) 如图,已知椭圆的左、右顶点为A1,A2,上、下顶点为B1,B2,记四边形A1B1A2B2的内切圆为C2.

(1)求圆C2的标准方程;

(2)已知圆C2的一条不与坐标轴平行的切线l交椭圆C1于P,M两点.

①求证:OP⊥OM;

解析(1)因为A2,B1分别为椭圆的右顶点和上顶点,则A2,B1坐标分别为(2,0),(0,1),可得直线A2B1的方程为x+2y=2,则原点O到直线A2B1的距离为d=则圆C2的半径r=d=故圆C2的标准方程为x2+y2=

(2) ① 可设切线l:y=kx+b(k ̸= 0),P(x1,y1),M(x2,y2),将直线PM的方程代入椭圆C1可得k2)x2+2kbx+b2−1=0,由韦达定理得

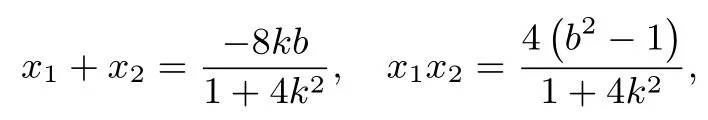
则y1y2= (kx1+b)(kx2+b) =又l与圆C2相切,可知原点O到l的距离d=整理得所以

故OP⊥OM.

②由OP⊥OM,当直线OP的斜率不存在时,显然|OP|= 1,|OM|= 2,此时当直线OP的斜率存在时,设直线OP的方程为y=mx,代入椭圆方程可得故OP2=x2+y2= (1 +m2)x2=同理,则

评注本题通过椭圆四顶点构成的内切圆这一条件,推出内切圆的切线与椭圆相交得到两交点P,M时,有OP⊥OM.这是我们推广结论1(3)的一个反推,更加有力证实了这个问题的多重变式和多元考查角度.

例2已知椭圆= 1(a > b >1) 内有圆x2+y2= 1,如果圆的切线与椭圆交A,B两点,且满足=0(其中O为坐标原点).则

解法一由于OA⊥OB,当A左(右)顶点,B为上(下)顶点时,直接利用结论1(3),圆x2+y2=与AB相切,所以=1;即

解法二由于OA⊥OB,当A左(右)顶点,B为上(下)顶点时,|AB|=又圆x2+y2= 1 与AB相切,圆心O到AB的距离为半径1,|OA|·|OB|= 1×|AB|,即

解法三设圆的切线的切点坐标为(x0,y0),则切线的方程为x0x+y0y= 1,与椭圆方程联立消去y得 (a2x20+b2y20)x2−2a2x0x+a2−a2b2y20= 0.设A(x1,y1),B(x2,y2),因=0,所以x1x2+y1y2=0,又x0x1+y0y1=1,x0x2+y0y2=1,所以

因x02+y02= 1,因此所以

评注本题解法一、二,本着小题小做的原则,巧用本文推广的结论解决问题.解法三则是较为严谨的通性通法,深思巧算.

五、反思感悟,且研且思

本文通过对一道模拟题的剖析,不仅发现了很多精彩的解法,还发现圆锥曲线中的一个垂直条件,其中蕴含了很多有关定值、定点、定圆、定轨迹等确定的结论.并将这些结论进行了引申应用,加深我们对数学本质的理解.正所谓“题在书外,根在书中”,对题目的深入探究,推广引申是促进数学教师专业成长的有效途径,同时也能更好的引领学生主动探索,归纳总结,更好的激发学生学习数学的兴趣和提升数学核心素养.