基于固支直杆弯曲小试样的P91/P92钢蠕变性能对比评价研究
2021-05-21余海洋周帼彦涂善东
韩 笑,余海洋,周帼彦,涂善东
(华东理工大学 承压系统与安全教育部重点实验室,上海 200237)
0 引言
近年来,超(超)临界机组已成为我国火力发电主流机组,随着火电机组参数和效率的提高,机组所选用钢材等级不断提高。P91/P92钢由于其较高的性价比及良好的性能,成为超(超)临界机组关键部件的主要材料类型[1],包括主蒸汽管道、再热蒸汽管道以及高温联箱等,如表1[2]所示。超(超)临界机组关键部件的服役温度范围为600~700 ℃,服役压力30.0 MPa,长期服役于该高温高压工况下,这些结构材料的性能劣化甚至断裂,不但缩短机组寿命,还会对热电厂的高效生产及安全性造成严重影响。其中蠕变断裂为主要的失效形式。因此对比分析P91/P92材料的高温蠕变性能及其影响因素,对火电机组关键部件的合理选材、高效设计以及安全运行具有重要意义。

表1 超(超)临界锅炉主要部件用钢
目前,国内外已对P91/P92钢材的蠕变性能进行了广泛的研究。BURTON等[3]提出了纯扭转的多轴螺旋弹簧蠕变试验法,并用于研究低应力下P91钢的短程蠕变行为,分析了低应力下组织退化对蠕变性能的影响。许乐等[4]对P92钢焊接接头蠕变损伤与裂纹扩展进行了有限元模拟,建立了裂纹萌生/扩展行为与热影响区宽度的关系。黄桥生等[5]对P92钢焊接接头进行高温持久试验,从微观角度分析了P92钢焊接接头蠕变损伤的形成机理。BENDICK等[6]总结了P92钢的蠕变强度外推方法,扩大了P92钢蠕变强度的预测范围。毕瑶等[7]通过蠕变持久和间断试验制备了具有不同蠕变损伤状态的P91钢试样,并利用3.5%NaCl电解液研究了P91高温蠕变损伤过程中的电化学极化行为,得到了蠕变损伤速率与组织的关系。上述这些研究都是将P91/P92系列材料作为一类材料,并未对两者进行具体的对比分析。然而二者化学成分有所不同,所表现出的力学性能以及对温度和压力的敏感性也不尽相同,导致其构件寿命和安全性的较大差异。因此,定量对比分析评估两种材料的高温力学性能,对超(超)临界机组的精确选材和安全生产具有关键性的决定作用。
为了尽可能减少对在役设备的损伤,国内外也不乏利用小试样方法对构件材料P91/P92的高温性能进行研究。秦炎锋等[8]采用P91材料,利用小冲杆法确定了该材料在一定温度下的Norton 参数;AL-ABEDY等[9]利用小冲杆试样,采用Kocks-Mecking Estrin模型评价了P91高温蠕变性能。SONG等[10]对比了小冲杆试样与单轴试样下的P92材料蠕变损伤特性,证明了小冲杆试样评价P92钢的蠕变性能相对于单轴试样的优越性。JEONG等[11]采用小冲杆蠕变的方法,对P92微观析出相和空洞的变化进行定量分析,得到了不同试验方式及加载方式对P92钢析出相和空洞变化的影响规律。然而相关研究表明,小冲杆试验法具有一定的局限性,其试样受力复杂,解析解较为困难,蠕变第三阶段非常短暂,可采集数据有限。相比之下,固支直杆弯曲小试样试验法[12-15]试样结构和受力简单,能够获得完整的蠕变三阶段曲线,在评价在役和非在役设备材料性能方面具有潜在的优越性[16]。因此,可以预见利用固支直杆小试样方法对P91/P92材料进行对比分析研究更方便,但其应用的可行性还需进一步验证。
本文考虑到经济性、耗时长短和试验精度等方面,主要基于固支直杆弯曲小试样方法,再在确定P91/P92材料合适的试样模型基础上,采用有限元方法对P91/P92材料的蠕变性能进行对比分析,并探讨其对载荷及温度的敏感性,为超(超)临界机组用钢正确经济的选取提供依据。
1 P91/P92 钢的理化性能
1.1 P91/P92钢化学成分
P91是在9Cr-1Mo钢的基础上,以Cr,Mo为主要固溶强化合金元素,在限制C含量的同时,严格控制P和S等残余元素含量,并添加N,V和Nb等元素形成的低碳低合金耐热钢,现阶段的服役温度为600~650 ℃,属于回火马氏体钢[17]。随着高参数、大容量超(超)临界机组的发展,P91钢的性能已经不能够满足日渐增长的蒸汽温度和压力的要求,于是P92钢应运而生。P92钢是在P91钢基础上开发的新一代F/M钢,主要采用增加W、减少Mo,同时加入少量的B及V,Nb的复合多元强化的手段开发出的[18],其高温蠕变强度和服役温度进一步提高。根据ASTM A-335,P91/P92钢的化学成分如表2[19]所示。

表2 P91与P92钢材料化学成分
1.2 P91/P92钢力学性能参数
ASME规范中,P91/P92钢的常温力学性能如表3[20]所示。

表3 P91与P92钢的力学性能
2 试样模型参数的确定
2.1 有限元模型的建立
本文采用ABAQUS进行数值模拟计算,对P91钢与P92钢的高温蠕变性能进行模拟对比分析。试样的有限元模型如图1所示,试样为矩形截面直杆试样,定义试样厚度为2h、宽度b、总长L、有效跨距l、压头半径r。

图1 固支直杆弯曲小试样有限元模型
蠕变本构采用Norton方程:
(1)
试样两端面直接固定(U1=U2=U3=0),恒定载荷P通过圆柱形压头施加在试样中心,约束压头除y方向以外的全部自由度。有限元模拟过程中摩擦系数取f=0.3,试样网格选用C3D8R类型,对试样压头中心和固定端等变形较大位置的网格进行加密,并且关闭几何非线性。
在本构模型方面,文献[12-13]中基于不同材料的试验结果,分析并修正了基于梁弯曲理论的固支直杆弯曲小试样模型,与单轴蠕变试验结果相比,其准确度较高。故本文采用了修正后的固支直杆弯曲小试样本构模型进行分析,其等效应力和应变公式[13]如下:
(2)
(3)
为进一步说明固支直杆弯曲小试样本构模型对于本文所研究的P91/P92材料的有效性,采用文献[21]中P91材料在650 ℃条件下的试验结果进行验证。图2为650 ℃下P91单轴拉伸试验与有限元模拟稳态蠕变应变速率对比图。由有限元模拟反演得到650 ℃下P91材料的Norton蠕变参数为:n=8.41,B=1.17×10-20,与文献[21]中试验结果n=8.234,B=2.472×10-20非常接近,蠕变指数n误差仅为2.11%,蠕变常数B在相同数量级。说明采用该本构模型和有限元方法对P91材料进行蠕变性能的模拟分析是可行且准确的。

图2 650 ℃下P91单轴拉伸试验与有限元模拟关系对比Fig.2 Comparison diagram of relationship between uniaxial tensile test and finite element simulation of P91 at 650 ℃
2.2 固支直杆弯曲小试样尺寸参数的确定
目前,固支直杆弯曲小试样方法的试验参数尚未统一,各个研究者选用的试样尺寸也不尽相同,导致得到的结果可比性较差。试样的压头尺寸及对中度、试样的尺寸、夹持端的结构等的不同,也会影响固支直杆弯曲评价蠕变性能的准确性。因此,为了排除试样尺寸对模拟结果的影响,保证结果的有效性及准确性,本文基于有限元法,运用上述模型,精确地控制各个参数的变化,模拟分析不同参数对固支直杆三点弯曲试样试验评价超(超)临界机组用钢蠕变性能的影响,以确定出最合适的模型参数。
2.2.1 试样有效跨距的确定
由图3所示的固支直杆三点弯曲试样受力简图可以看出,试样受集中载荷发生横力弯曲,试样跨距同厚度满足一定条件成为细长梁时,切应力的影响可以忽略,此时横力弯曲问题简化为纯弯曲问题[22],三点弯梁横截面上的最大切应力与最大正应力之比为:
(4)
当2h∶l=1∶10时,最大切应力仅为正应力的10%,可以忽略。考虑固支直杆三点弯曲小试样固定端约束较大,选取最大比例为:2h∶l=1∶12。为了考虑有效跨距的影响作用,分别选取10,12,14,16四组尺寸,利用P91钢分别在两种最优宽厚比(b∶2h=1∶1和b∶2h=2∶1)[15]下进行模拟。P91钢稳态蠕变应变速率与应力的曲线见图4。
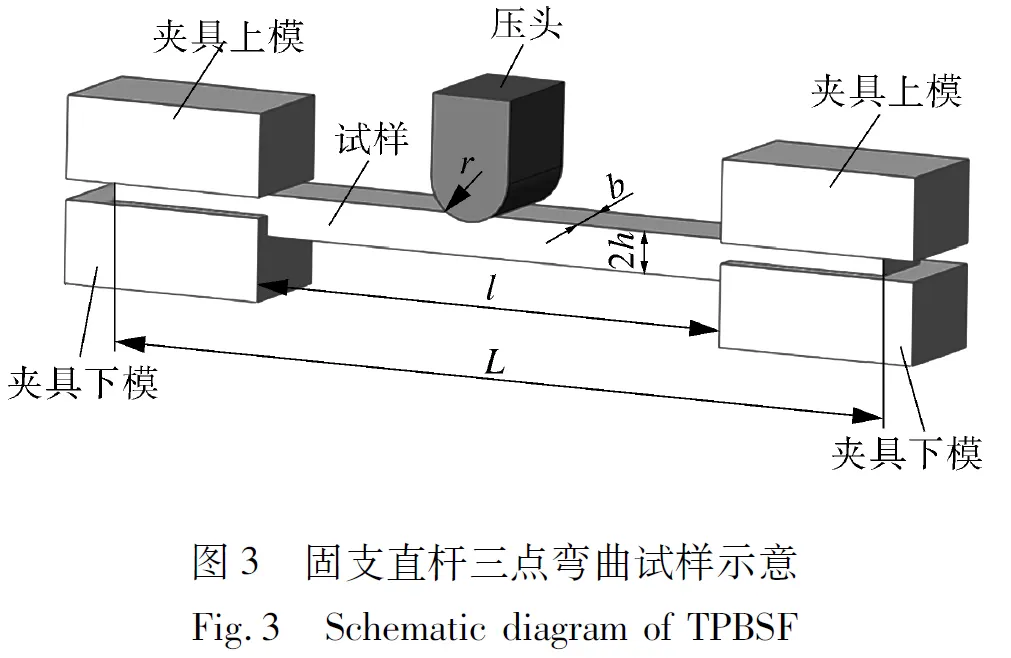
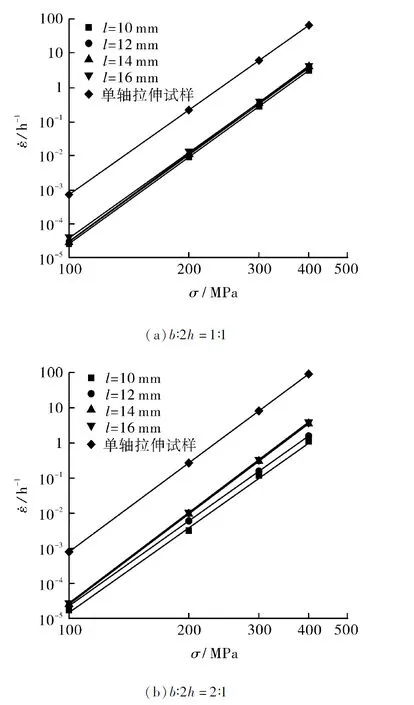
图4 P91材料稳态蠕变应变速率与应力σ关系曲线
模拟结果与单轴拉伸试样的稳态位移速率误差如表4所示。随着有效跨距的增大,三点弯曲试样的模拟结果与单轴拉伸试样结果的偏差减小,但有效跨距对模拟结果的影响不大,偏差减小量均小于0.04,所以考虑到尽量减小试样的尺寸,选取有效跨距为l=10 mm和l=12 mm两种尺寸进行后续模拟。

表4 不同有效跨距的试样与单轴试验对比误差
2.2.2 试样具体宽厚尺寸的确定
文献[15]中经过与单轴试验的稳态应变速率-应力曲线对比可知,当横截面的宽厚比b∶2h=2∶1时,选择过渡段倾斜角(如图5所示)为30°的试样最优;当横截面的宽厚比b∶2h=1∶1时,选择过渡段倾斜角为45°的试样最优。

图5 过渡段结构示意
因此,选择固定的宽厚比为b∶2h=2∶1和b∶2h=1∶1两种比例,并改变具体几何尺寸,利用P91材料进行模拟,分析具体尺寸对模拟结果的影响。P91钢稳态蠕变应变速率与应力的关系曲线如图6所示。
由模拟结果可以看出,当有效跨距l=10 mm时,其整体趋势均是随着尺寸的增大,与单轴拉伸试验的拟合度越高,但误差均在90%以上;当有效跨距l=12 mm时,拟合度更高,整体呈现出随着尺寸增大,与单轴拉伸试验的拟合度先增大、后减小的趋势,并且在b=2h=1.1 mm,l=12 mm的尺寸时达到最高的拟合度。
2.2.3 试样压头尺寸的确定
设计不同压头直径与压头偏心距进行有限元模拟,模拟结果如图7,8所示。由图7可以看出,曲线均较为平稳,压头直径对模拟结果影响不大,所以沿用前人[12]所选取的压头直径2.0 mm。由图8可以看出,当偏心距大于0.3 mm时,曲线开始出现轻微的上下波动,偏心距对于模拟结果的影响开始显现出来。为了控制试验误差,偏心距应控制在0.3 mm以内。

图6 P91钢稳态蠕变应变速率与应力σ的关系曲线

图7 压头直径D与稳态位移速率关系

图8 压头偏心距e与稳态位移速率关系
综合以上模拟结果,最终确定模拟所采用的固支直杆三点弯曲试样的尺寸为:厚度2h=1.1 mm、宽度b=1.1 mm、总长L=20 mm、有效跨距l=12 mm、压头直径D=2.0 mm。利用此尺寸的固支直杆三点弯曲试样进行后续P91/P92材料的蠕变性能对比评估,可以有效地忽略试样尺寸对模拟结果产生的影响。
3 P91/P92 钢蠕变性能对比分析
3.1 P91/P92钢蠕变性能对比
利用上述确定的尺寸形式的固支直杆三点弯曲小试样模型对P91/P92材料的蠕变性能进行模拟对比。650 ℃下P92钢的蠕变参数为:n=7.69,B=2.12×10-19[23]。
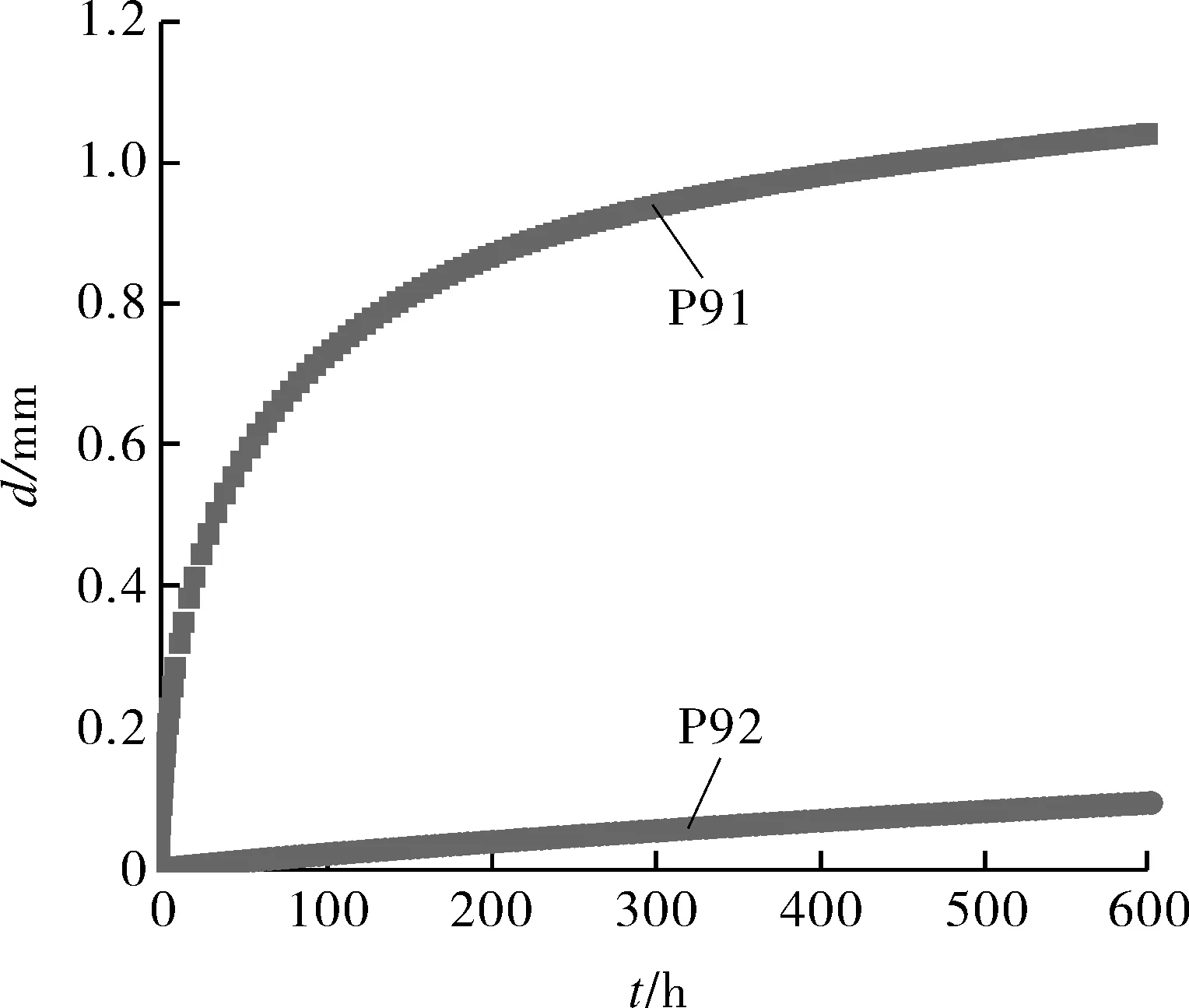
图9 P91和P92试样中心位移d与时间t曲线对比
在650 ℃下,当载荷为30 N时对应的两种材料的中心蠕变位移d和时间t的曲线如图9所示。可以看出,P91/P92材料中心位移-时间曲线相差较大,在相同载荷下,P91钢试样的中心位移迅速增加,在200 h左右达到稳态蠕变状态;P92钢试样的中心位移速率远远小于P91钢,且基本保持不变。P92钢作为新型第三代超(超)临界机组用铁素体耐热钢,相比于P91钢来说,其高温持久强度和蠕变性能有了明显提高。
3.2 P91/P92钢蠕变性能对载荷的敏感度对比
两者在相同应力下的稳态蠕变应变速率的数值比较如表5所示。定义应变速率增率υ,其计算公式如下:
(5)

图10 P91和P92钢稳态蠕变应变速率与应力σ

表5 P91/P92钢稳态蠕变应变速率对比
由表5可知,在小于400 MPa的应力范围内,P91钢的应变速率增率大于P92钢的应变速率增率,即P91材料的蠕变性能对于载荷的变化更加敏感。在相同应力水平下,P91钢的稳态蠕变应变速率比P92钢高出约20~200倍,可见在P91钢基础上改进后的P92钢具有更优良的蠕变性能。
3.3 P91/P92钢蠕变性能对温度的敏感度对比
查阅相关文献,得到P91钢在580,600,620,625,650 ℃和P92钢在595,610,625,640,650 ℃下的蠕变参数分别见表6,7[24-28]。

表6 P91钢蠕变参数

表7 P92 钢蠕变参数
为了验证固支直杆三点弯曲小试样本构模型对所有温度工况的适用性,分别对5个温度工况下P91材料的蠕变性能(5个载荷工况)进行了有限元模拟分析,并与对应工况条件下的单轴蠕变试验结果[24-25]进行了对比,结果如表8所示。可以看出,由固支直杆三点弯曲有限元模拟所得的蠕变参数n和B与同工况下由单轴蠕变试验得到的结果较为接近,蠕变指数n最大偏差小于10%,蠕变常数B均在相邻数量级。说明该模型不受温度工况条件的影响,且准确性较高。

表8 P91钢单轴蠕变试验与固支直杆三点弯曲有限元模拟所得的蠕变参数对比
在此基础上,在50 N的载荷下进行模拟,对比P91/P92钢蠕变性能对温度的敏感度。模拟结果如图11所示。

(a)P91钢
图12示出P91/P92钢材料的稳态位移速率-温度变化情况。可以看出,随着温度的升高,P91和P92材料的稳态位移速率均逐渐升高;在相同温度条件下,P92钢的稳态蠕变位移速率明显小于P91钢,且两者对于温度变化都较敏感。
为进一步对比考察两种材料对温度的敏感性,定义蠕变速率温度系数η(见公式(6))。计算得P91钢、P92钢在温度低于625 ℃时,蠕变应变速率温度系数分别为0.005 2 mm/(h·K)和0.003 8 mm/(h·K);在温度高于625 ℃时,P91钢、P92钢的蠕变应变速率温度系数分别为0.002 1 mm/(h·K)和0.004 5 mm/(h·K)。由此可见,小于625 ℃时,P91材料的蠕变性能对于温度更敏感;而高于625 ℃时,P92材料对温度更敏感。因此,综合考虑选材的经济性和可靠性,在温度低于625 ℃时可优先选用P92钢。
(6)
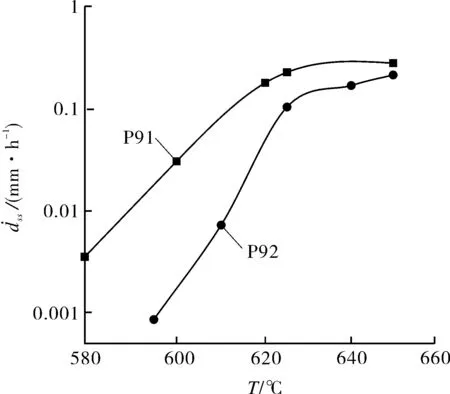
图12 P91/P92钢稳态位移速率温度(T)
4 结论
本文基于固支直杆三点弯曲小试样梁弯曲本构模型,采用有限元模拟的方法,确定了用于研究超(超)临界机组材料高温力学性能的固支直杆三点弯曲小试样模型尺寸,并基于该尺寸模型对比分析了P91/P92钢的蠕变性能。得到主要结论如下。
(1)用于研究超(超)临界机组材料高温力学性能的固支直杆三点弯曲小试样模型合理尺寸为b=2h=1.1 mm,l=12 mm,其中有效跨距l对固支直杆三点弯曲小试样评价蠕变性能的影响不大,但当宽厚比固定为b∶2h=2∶1和b∶2h=1∶1时,有效跨距的影响较大。
(2)在650 ℃,30 N载荷下,P92钢中心位移比P91钢有大幅下降,在600 h时,P92钢中心位移仅为P91钢中心位移的10%,可见P92在高温下具有更好的抗蠕变性能。
(3)在100~400 MPa应力范围内,P91材料的蠕变性能对于载荷的变化更加敏感,在相同应力水平下,P91钢的稳态蠕变应变速率比P92钢高出约20~200倍,故在高应力条件下优先选用P92钢。
(4)考虑温度敏感性,在温度低于625 ℃时,P91材料的蠕变性能对温度变化更敏感,可选用P92钢;在温度高于625 ℃时,P92钢的蠕变性能对温度变化更敏感,但两者差距不大,在保证设备安全性的前提下,考虑到选材的经济性,可选用P91钢。
