基于数据背景下采用“模拟退火算法”确定太阳影子定位

①张妍　②赵璐　③雷晓

一、问题分析

该问题要求根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的具体地点与日期。

采用超定方程组求解。但所求地理位置与日期不准确，存在所求点位于夜半球等情况，与实际情况与地理常识不符。未知量增多，除却求直杆经度、纬度、杆长，还需求出拍摄日期。且目标函数为非线性函数，为多变量复杂优化问题，故采用模拟退火（Simulated Annealing Algorithm）解决该问题。

二、模型建立与求解

（一）模型的准备

1、对直杆所处地理位置进行范围缩小

基于太阳直射点运动规律，北京时间为12：41时，求得109.75°E时间为12：00，进而推算出昼半球范围为（19.75°E，161.25°W），而只有西昼半球会随着地球自转，影子逐渐变短，符合附件二影长变化规律，直杆合理位置精确至（19.75°E，109.75°E）。进一步精确范围，由于该题以一个小时为时间间隔，（94.75°E，109.75°E）会在一个小时内随地球自转进入夜晚，后期影子会逐步消失，与附件二所给影长一直减短的趋势矛盾。最终，直杆合理位置精确至（19.75°E，94.75°E）。

2、对直杆所处地理位置进行范围缩小

北京时间为13：09时，求得102.75°E时间为12：00，进而推算出东昼半球范围为（102.75°E，167.25°W），因为只有东昼半球会随着地球自转，影子逐渐变长，符合附件三影长逐步延伸的规律。进一步精确范围，由于该题以一个小时为时间间隔，（177.75°E，167.25°W）会在一个小时内随地球自转进入夜晚，后期影子会逐步消失，与附件三所给影长一直延伸的趋势矛盾。最终，直杆合理位置精确至（102.75°E，177.75°E）。

（二）基于模拟退火建立确定直杆日期的模型

模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。具体解题步骤如下：

Step1：建立解空间。

依据附件二与附件三所给直杆影长值，以及模型准备阶段已经确立的附件二直杆所处位置合理的经度范围（19.75°E，94.75°E），附件三直杆所处位置合理的经度范围（102.75°E，177.75°E），建立解空间如下：

利用选定的降温系数α[进行降温，取新的温度K为αK（这里K为上一步迭代的温度），这里选定α=0.999。

Step6：结束条件。

用选定的终止温度e=1013。，判断退火过程是否结束。若K

（三）确定直杆日期模型的结果分析

1、结果分析

基于模拟退火法在全局范围内搜索，找到直杆所处地理位置与所在日期的最优解，如下表所示：

表1 直杆地理位置

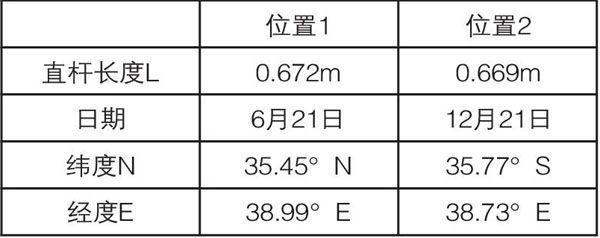
分析上表可知，6月21日在（35.45°N，38.99°E）处存在一长为0.672米的直杆;12月21日在（35.77°N，38.73°E）处存在一长为0.669米的直杆。

根据上述结果全面思考，当6月21日时太阳直射纬度为23.25°N，基于假设1地球是一个规则球体，以太阳直射纬度23 25。N为对称轴，存在与（35.45°N，38.99°E）南北對称的另外一点;同理，12月21日时太阳直射纬度为23.25°S，以太阳直射纬度23.25°S为对称轴，也存在与（35.77°N，38.73°E）南北对称的另外一点：

表2 关于太阳直射纬度对称的直杆位置

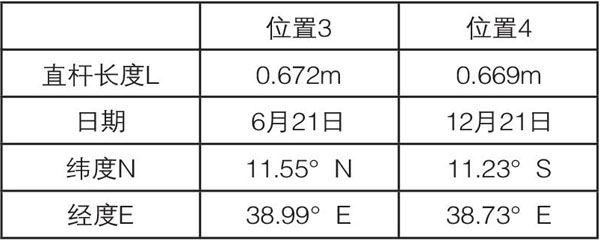
2、结果分析

基于模拟退火在全局范围搜索，找到附件三直杆所处地理位置与所在日期的最优解，如下表所示：

表3 直杆地理位置

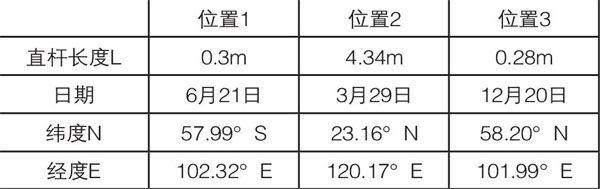
分析上表可知，6月21日在（57.99°S，102.32°E）处存在一长为0.3米的直杆;3月29日在（23.16°N，120.17°E）处存在一长为4.34米的直杆;12月20日在（58.20°N，101.99°E）处存在一长为0.28米的直杆。

观察所求位置深入思考，当6月21日时太阳直射纬度为57.99°S，基于假设1地球是一个规则球体，以太阳直射纬度57.99°S为对称轴，不存在与（57.99°S，102.32°E）南北对称的另外一点;当12月20日时太阳直射纬度为58.20°N，以太阳直射纬度58.20°N为对称轴，不存在与（58.20°N，101.99°E）南北对称的另外一点;当3月29日时太阳直射纬度为23.16°N，以太阳直射纬度23.16°N为对称轴，存在与（23.16°N，120.17°E）南北对称的一点，该点具体信息为：日期为3月29日，直杆长为434米，位于（20.02°S，120.17°E）。故直杆可能存在的位置共有四个。