管系弹性跟随效应对容器-接管连接的应力分析评定影响研究
2021-05-21张向兵段成红陆明万罗翔鹏
张向兵,段成红,陆明万,罗翔鹏
(1.北京化工大学 机电工程学院,北京 100029;2.清华大学 航天航空学院,北京 100084)
0 引言
基于化工过程生产的特点和热胀冷缩的材料特性,处于高温环境下的管道犹如一个被压缩的弹簧,对相连接的容器管口产生一定的推力作用,因此在进行容器应力分析和设计时,应当考虑管道热膨胀引起的管系热胀载荷。分部法和整体法是容器应力分析时处理管系热胀载荷的两种方法。分部法将管系和容器解耦,进行单独分析,即配管专业将容器管口视为刚性,以固定约束作为管系与容器管口连接一端的边界条件,对管系施加热载荷单独分析计算,由固定端支反力得到管系作用力并将其提交给容器专业,容器专业再将该作用力施加至容器管口,对容器单独进行应力分析[1];整体法则是将管系和容器整体建模,对管系施加热载荷进行整体耦合分析[2-3]。
但采用不同方法处理管系热膨胀载荷时,容器接管根部的局部应力评定[4]都是一个比较复杂的问题。在应力分类法中热应力属于二次应力,可以按照二次应力准则进行评定,允许容器沿壁厚截面发生局部塑性变形,只要能保证结构处于安定状态[5]。但是若在相连接的两个强度相差较大结构中强度较弱的那个结构先发生塑性变形,将会出现弹性跟随效应[6],引起应变集中现象[7]。从保守考虑,各国规范要求将容器因管系热胀载荷引起的薄膜和弯曲应力按照一次应力准则进行评定。
弹性跟随效应最初由美国的ROBINSON[8]提出,用于解释螺栓连接因为高温蠕变产生的松弛行为,之后KASAHARA[9]将其引入局部塑性和几何非线性对结构响应的影响,通过对裙座结构不连续处发生塑性时的弹性跟随现象进行分析,发现结构会由于弹性跟随效应出现应变集中。桑如苞等[2]通过理论分析认为,分部法处理管系热膨胀引起的附加载荷不涉及对结构变形的控制,不能保障容器管口部位的安定性[2]。秦叔经[6]也提到基于应力分类方法的思想,即采用弹性分析的方法处理弹塑性材料的变形和强度问题,不能反映是否出现应变集中导致分析结果不安全。
本文基于双杆模型对管系弹性跟随效应进行理论分析和说明,以标准椭圆封头带中心接管结构为例,分别采用分部法和整体法在一定管系热载荷下进行线弹性对比分析,在循环载荷下进行弹塑性计算,对塑性应变场进行差值计算,评定结构是否处于安定状态,揭示管系弹性跟随效应在容器应力分析中对容器应力评定结果的影响规律。
1 管系热膨胀载荷的弹性跟随效应
对于管道热膨胀引起的作用于容器管口的管推力,管道专业在单独对管道进行分析时,将管系两端设为固定约束,对管道施加热载荷进行求解,若将管系简化为一段长度为L的直管,管道材料的线膨胀系数为α,管系温升为ΔT,则管系自由膨胀量ΔL为:
ΔL=αΔTL
(1)
设管道材料弹性模量为E,管道截面积为A,则在管道两端固支(即管系热膨胀被完全约束)情况下管推力FN0为:
FN0=αΔTEA
(2)
由公式(1)(2)可以看出,管推力的大小与管道长度无关,但管道的热膨胀量与管道长度有关,此变形量将由容器和管系共同吸收。若将管系及其连接的容器简化为串联的两个杆件,杆件两端固定,如图1所示。分别将对应于容器和管系的杆件记为V和P,截面积分别为AV和AP;在两杆件均为弹性的情况下,由热膨胀引起的连接处的轴力为F;KV和KP分别为容器和管系的轴向刚度,ΔV和ΔP分别为容器和管系在轴力为F时的变形量。
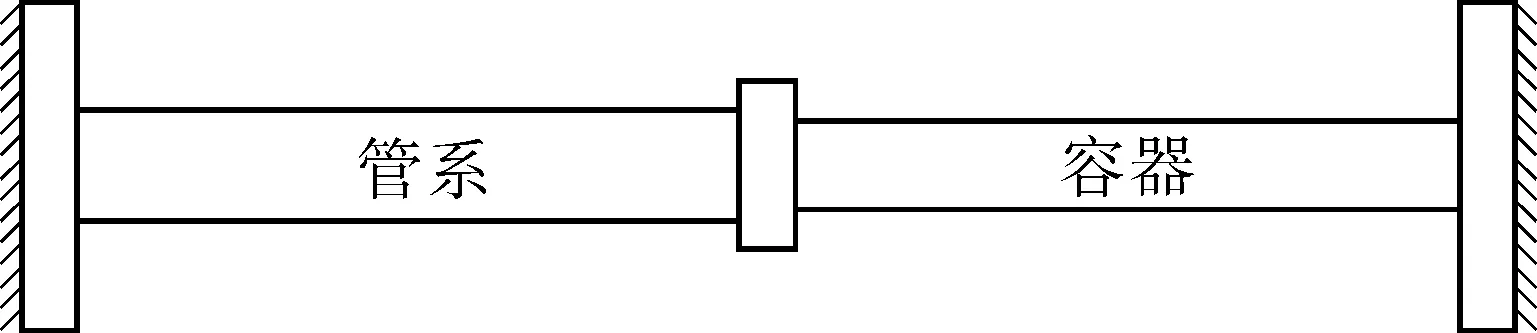
图1 双杆模型结构示意
管系受热膨胀引起的热膨胀量由容器和管系的变形共同吸收,因此:
ΔL=ΔV+ΔP
(3)
容器与管系相比强度较低,因此在一定载荷作用下将率先出现塑性变形,当容器对应较弱杆件V的应力达到对应材料的屈服强度σS(即轴力达到杆件的极限载荷),管系对应杆件P仍处于弹性状态,两杆间实际作用力F′=σSAV,F′≤F。
弹性杆的实际变形量为:
Δ′P=F′/KP
(4)
其余热膨胀量全部由塑性杆V吸收,变形量为:
Δ′V=ΔL-Δ′P
(5)
弹性及弹性理想塑性条件下对应的双杆模型载荷-位移曲线如图2所示。
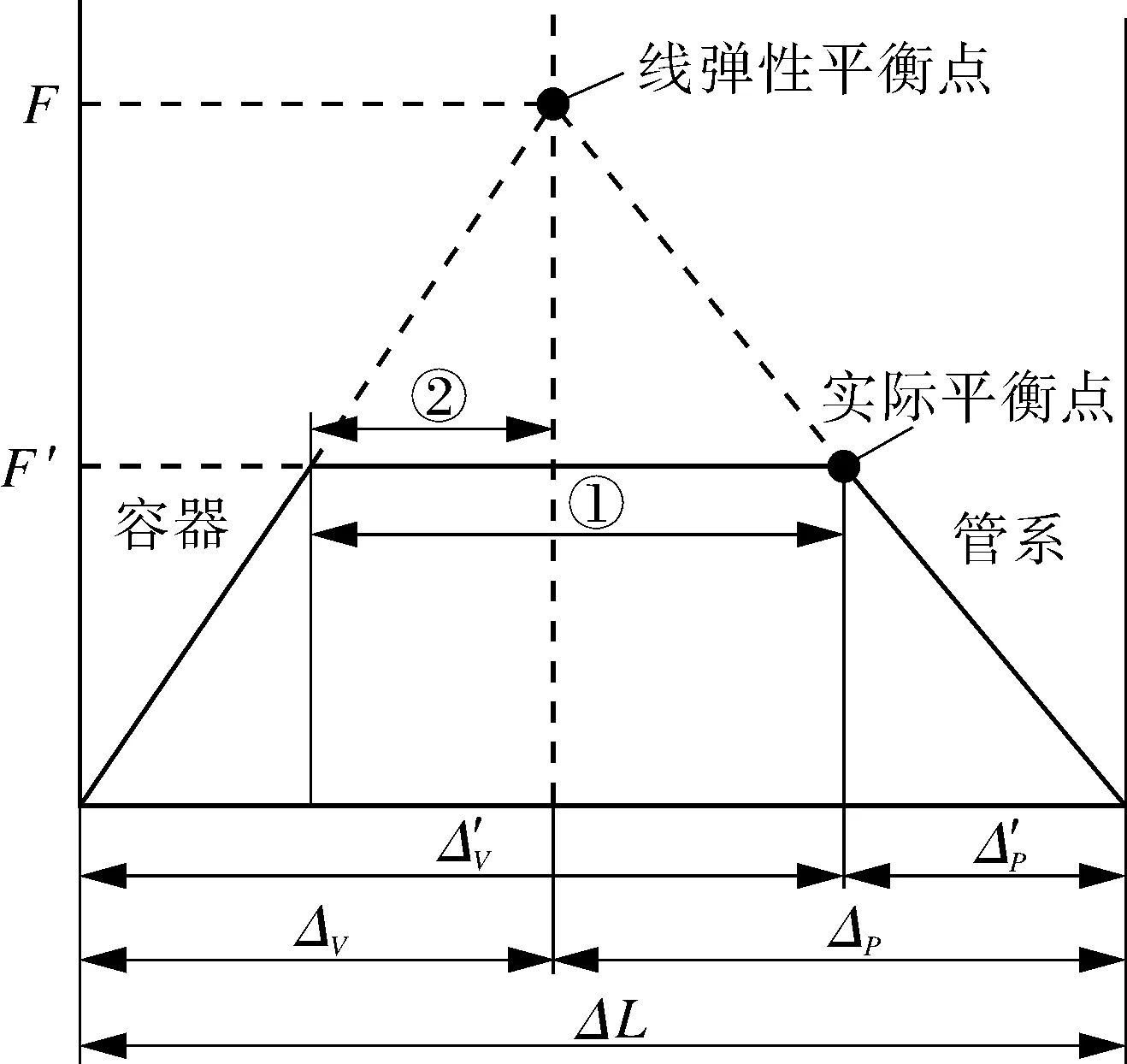
图2 双杆模型载荷-位移曲线
从图2可看出,Δ′V为容器(杆V)实际吸收的热膨胀量,其中①为塑性变形;ΔV为弹性条件下容器(杆V)吸收的热膨胀量,其中②为假想杆V始终保持弹性时的名义塑性变形。对于双杆模型,当较弱杆件承受的轴力达到材料的屈服极限,杆件将进入塑性流动状态,可以无限制变形,因为弹性杆P始终处于弹性状态,弱杆将吸收其余的热膨胀量,使得①>②,容器实际应变大于理论应变,由于弹性跟随效应而出现应变集中现象。
2 管系弹性跟随的有限元计算
本文采用有限元分析方法对管系热膨胀载荷的弹性跟随问题进行分析。利用ANSYS有限元分析软件,以标准椭圆封头中心接管结构为例,基于二维轴对称模型,分别按照分部法和整体法进行线弹性分析及弹塑性分析,并进行对比研究。
2.1 几何尺寸及材料参数
分析模型的几何尺寸及设计参数如表1所示,容器及管道材料性能参数如表2所示。

表1 模型几何尺寸及设计参数
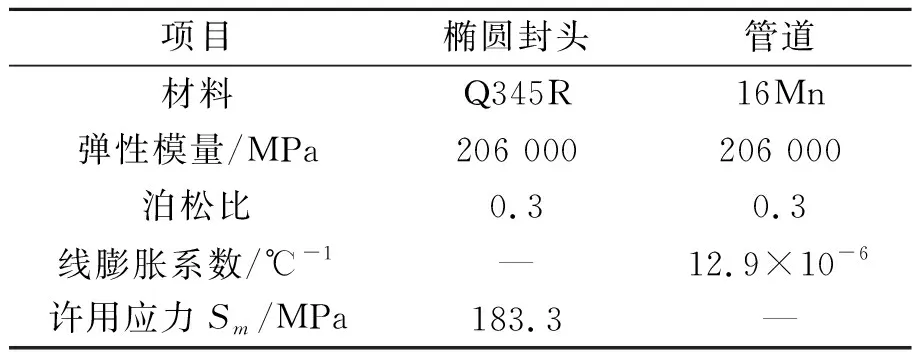
表2 容器及管道材料性能参数
2.2 分部法及整体法弹性分析
2.2.1 一次应力控制
分部法将管系和容器分为两部分单独计算分析,管系按照两端固支施加对应温度载荷计算管推力,再将管推力以机械载荷的作用方式施加至容器管口,对容器进行单独分析。本文将容器外接管系简化为一定长度的直管进行分析,直接采用解析解,不再单独建立有限元模型进行分析计算,其在一定温度载荷下产生的管推力可由公式(2)理论求解。
对于容器部分,仅对封头和接管进行建模分析,按照表1对应几何尺寸建立标准椭圆封头和接管的二维轴对称模型,因为本文主要关注容器部分在管系热膨胀载荷下的响应情况,因此暂不考虑内压,仅考虑管系推力单独作用。首先在容器管口施加管推力载荷20 MPa,在封头直边段底端设置竖直方向位移为0,几何模型及载荷约束条件见图3(a)。采用二维8节点Plane 183单元,容器-接管连接处网格划分见图3(b)。
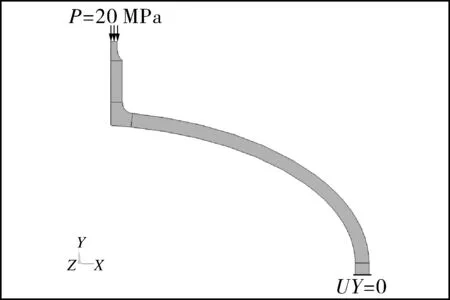
(a)模型及载荷约束条件
按照弹性材料模型求解计算,得到的von Mises应力分布云图如图4所示。在容器-接管连接处应力较大位置沿接管壁厚方向建立2条路径(见图4),应力线性化处理后的局部薄膜及薄膜加弯曲应力如表3所示。
按照基于弹性求解的应力分类法,一次局部薄膜应力和一次薄膜加弯曲应力的许用应力强度极限值为1.5KSm(K值为载荷组合系数,按照JB 4732—1995《钢制压力容器——分析设计标准》 (2005年确认)中表3-3取K=1.0),根据表2可得许用值1.5Sm=275 MPa。由表3应力线性化结果可知,在当前载荷下对应的局部薄膜加弯曲应力最大值为51.95 MPa,小于许用应力值,当局部薄膜加弯曲应力满足1.5Sm时,允许的管口推力载荷值为105.87 MPa(20×275/51.92)。
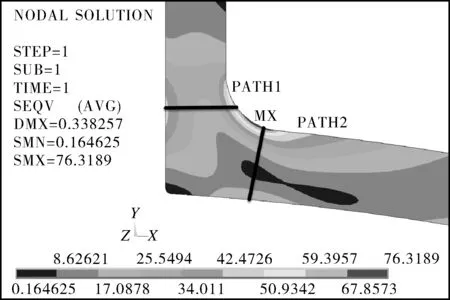
图4 20 MPa线弹性von Mises应力分布云图
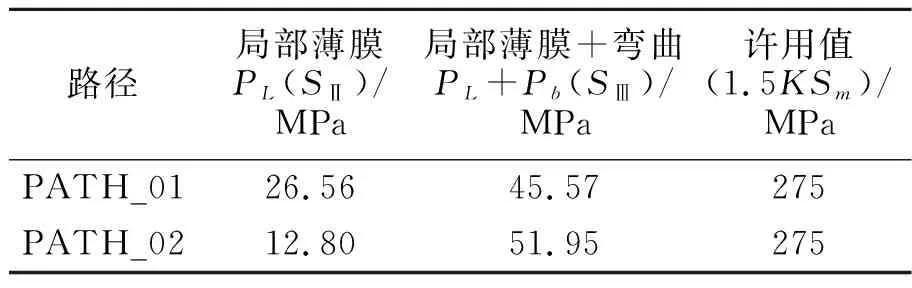
表3 20 MPa管推载荷下容器应力线性化结果
由公式(2)可知,当管系两端固支时,管系热膨胀引起的管系推力与管道长度无关,仅与温升条件有关,根据表2中管道材料的性能参数,可求得管推力为105.87 MPa对应的管道温升载荷为39.84 ℃。将管系和容器整体建模,对管系施加39.84 ℃的温升载荷条件,设置管系远离容器的另一端及封头直边段底端竖直方向位移为0,整体法几何模型如图5所示。
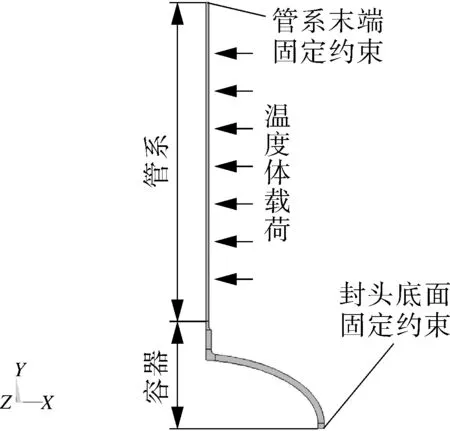
图5 整体法几何模型及约束示意
分别对5,10,20,40,80,160,320 m等7个不同管系长度条件下的模型进行弹性应力分析,并在容器-接管连接处的危险截面沿垂直壁厚方向建立路径,进行应力线性化处理,外接管系长度为5 m时的应力分布云图与路径设置如图6所示,不同外接管系长度对应的路径线性化应力结果如图7所示。
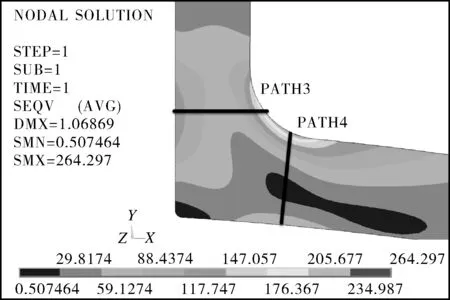
图6 应力分布云图及路径设置
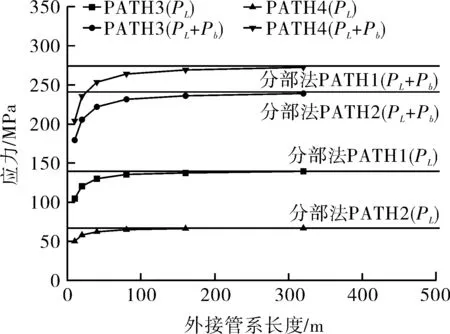
图7 不同长度管系对应的容器线性化应力
当用分部法计算时,管推力以机械载荷的形式施加到容器管口上,如前所述,两端固支的不同长度的管系在同一温升载荷条件下得到的管推力都相同,所以图7中由管推力引起的容器应力曲线不随管系长度而变化,都是水平线。当用整体法计算时,管系的一端固定,另一端与容器相连,容器的变形将使管系被约束的热膨胀量得到释放,导致管推力载荷减小,所以无论管系长度如何,整体法得到的容器应力均小于分部法的计算结果。在同一温升载荷条件下,管系的热膨胀量随管系长度正比增加,相应地,管推力也应正比增加;但另一方面,管系越长、轴向刚度越小,能吸收的热膨胀量越大,管推力将相应地减小,综合这两种影响,图7中整体法得到的容器应力曲线随管道长度的增加而增加,但增加量越来越小,并最终趋于分部法的计算结果。
由于分部法此时将管推力引起的应力按照一次应力进行控制,不允许容器沿壁厚截面发生塑性变形,因此,若分部法中按照一次应力校核通过,则认为其满足静强度要求,除峰值应力引起的疲劳之外,其不存在安定性问题。因为不同外接管系长度条件下容器应力结果均小于分部法计算结果,则其他外接管系长度条件下实际结构均满足静强度和安定性要求。
2.2.2 二次应力控制
若将管系热膨胀产生的管推力作用在容器管口引起的应力归属于热应力部分的二次应力,认为基于弹性分析结果的应力分类法,将其按照二次应力进行控制,允许结构发生局部塑性变形,但若应力满足弹性安定条件(应力小于3Sm),则结构处于安定状态,不会在载荷加载、卸载过程中出现应变增量而产生渐增性塑性变形失效。
由于采用弹性本构模型求解,应力结果与载荷值成正比例关系,因此由前文分析中的求解结果可知,若按照应力分类法将名义应力按照二次应力准则进行控制,允许应力强度极限值3Sm=550 MPa,对应的分部法允许载荷极限值为211.74 MPa(2×105.87),对应的允许管系温升载荷条件为79.68 ℃(2×39.84)。参照前文分析结果,在分部法满足应力评定要求时,整体法在对应温升载荷条件下应力均小于分部法计算结果,即也满足应力评定要求,因此,在分部法中,若将弹性求解管推力引起的应力按照归属于热应力的二次应力处理,则认为不论外接管系长度多少,容器允许的管道温升载荷极限值为79.68 ℃,即在这个温升范围内容器均满足静强度及安定性要求。
2.3 整体法弹塑性分析
由于将管推力引起的应力按照一次应力控制时,不允许容器沿壁厚截面出现塑性变形,除峰值应力引起的疲劳外,结构整体处于弹性状态,若按照一次应力校核通过,则认为容器满足静强度和安定性要求,本节不再对其进行详细的非线性弹塑性分析。
将管推力引起的容器应力按照二次应力进行评定时,允许结构沿壁厚出现塑性变形,为校核评定结果是否满足安定性条件,本节基于整体模型,采用弹性理想塑性本构模型进行循环载荷分析,材料本构模型(不考虑材料的强化效应)如图8所示。安定状态是指在载荷多次的加载、卸载过程中,结构不会产生累积的塑性变形[10-11]。本节在弹塑性分析时设置50个载荷步,以按照二次应力进行控制允许的最大温升载荷条件79.68 ℃,第一步施加管系热载荷,第二步卸载,第三步重新施加管系热载荷,……。对于不同长度的外接管系分别计算,通过APDL(ANSYS Parametric Design Language)提取结构各节点在不同载荷步下的塑性应变结果,并通过利用软件中的数组工具对结果进行差值计算,观察结构在加载、卸载过程中是否出现塑性应变增量。以长度条件5 m和320 m的结构的塑性应变差为例进行对比分析,在长度5 m的外接管系条件下,结构在第1次卸载后的塑性应变场如图9所示,容器-接管连接处出现局部塑性变形,两种管系长度条件下容器第25次卸载减去第1次卸载的塑性应变场差值结果如图10,11所示。
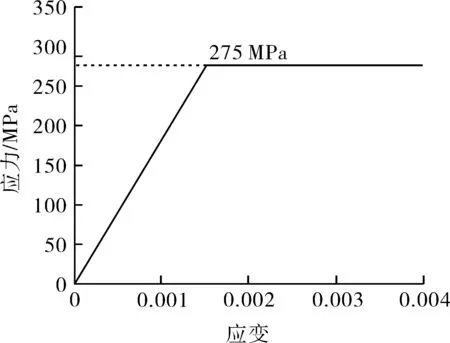
图8 弹性-理想塑性本构模型
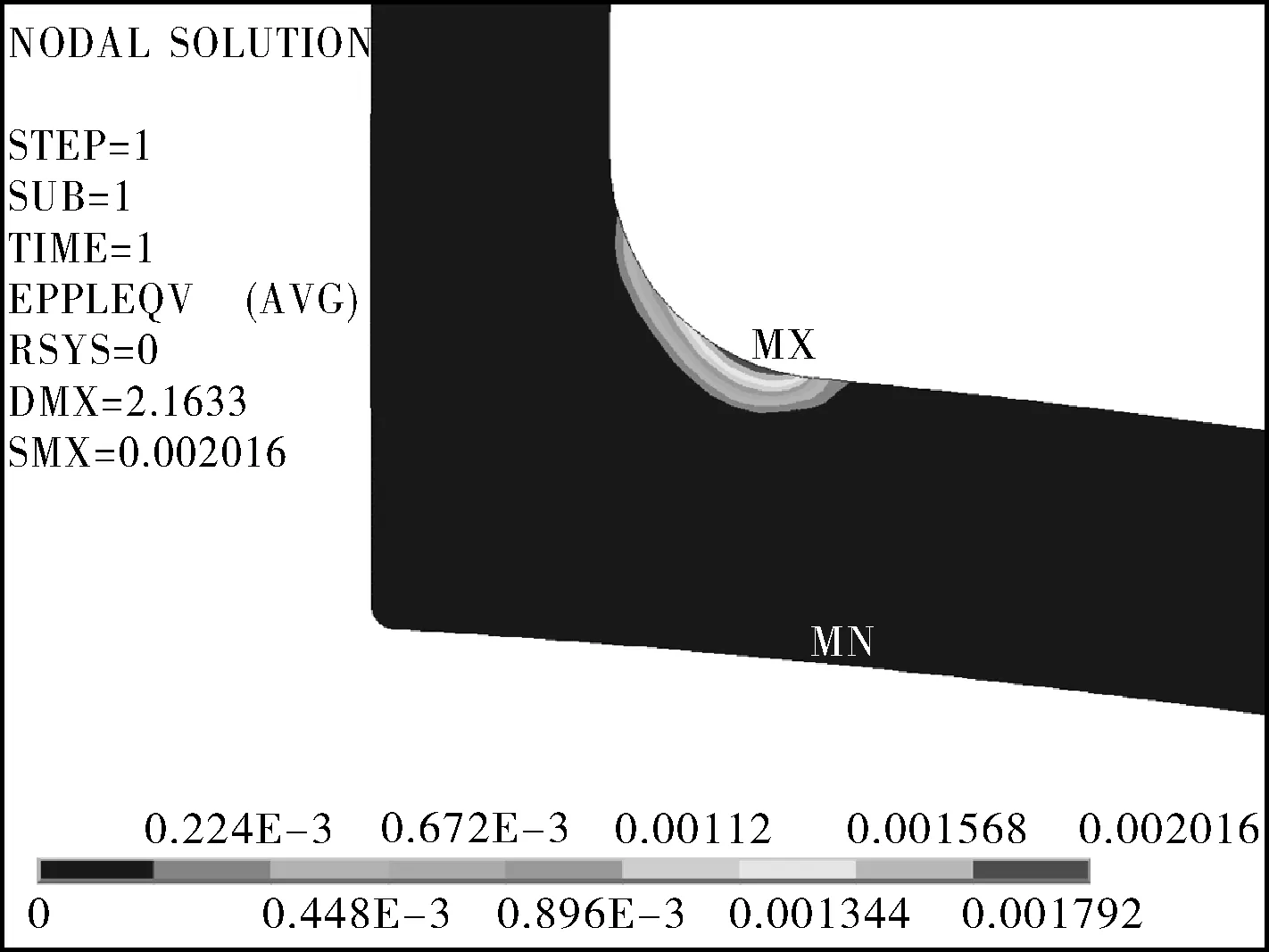
图9 长度条件5 m时容器第1次卸载后的塑性应变场
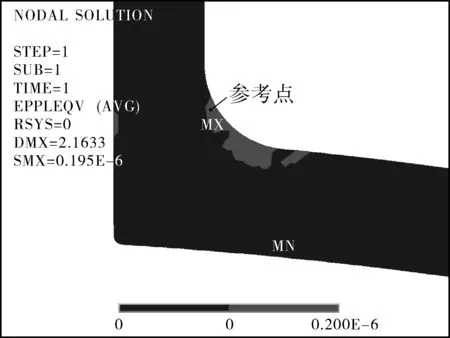
图10 长度条件5 m时容器第25次卸载减去第1次卸载的塑性应变场差值
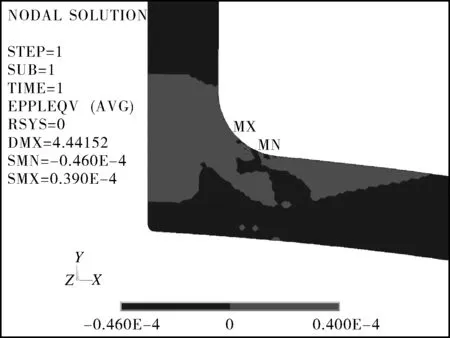
图11 长度条件320 m时容器第25次卸载减去第1次卸载的塑性应变场差值
从图10,11可看出,由于管系弹性跟随效应的存在,结构实际的塑性变形比在弹性条件下进行分析评定对应的假想塑性变形要大。在管道长度较小、管道刚度较大时,弹性跟随效应较小,容器局部出现塑性变形,但沿壁厚始终存在弹性核,沿壁厚没有产生渐增的累积塑性变形;当管道长度较长、管道刚度较小时,弹性跟随效应严重,此时结构中没有弹性核,容器沿壁厚出现累积塑性变形。
选取容器接管根部塑性应变不为0的位置节点作为参考点(见图10),同一节点在不同管长条件下塑性应变随载荷步的变化情况如图12所示,短管道对应节点除初始几个循环有变化外,在后续载荷循环下保持稳定,长管道对应节点出现累积塑性应变,在载荷循环条件下应变不断增加。选取容器管口端面中间节点沿管口轴向的位移作为观察对象,在两种管长条件下,位移随载荷循环次数的变化如图13所示,可以发现,在同一温升载荷条件下,短管道对应容器端面位移在后续载荷循环下呈现出稳定状态,长管道对应容器端面位移不断增加,结构尺寸出现永久性变形,容器处于不安定的棘轮状态。
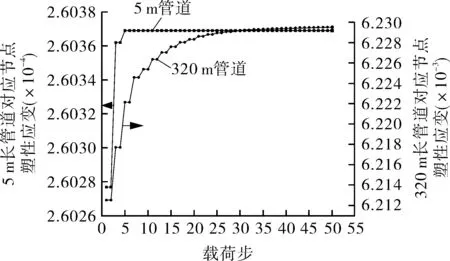
图12 节点塑性应变随载荷步变化曲线
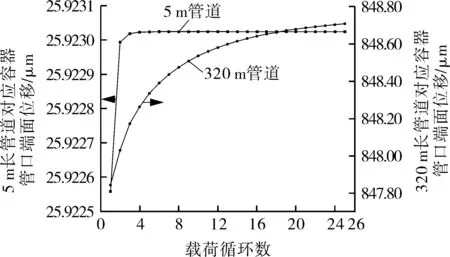
图13 不同管道长度对应容器管口端面中间节点位移随载荷循环变化曲线
保持容器模型一致,通过调整外接管道长度来调整其热膨胀量,对不同管道热膨胀量的热膨胀管系-容器系统整体进行循环载荷下的弹塑性分析。发现在管道较长、管道热膨胀量较大时,管系弹性跟随效应明显,此时在分部法中按照一次应力评定,不允许结构沿壁厚发生塑性变形,设计较为安全,按照二次应力评定允许结构沿壁厚出现塑性变形,则管系的弹性跟随会使容器出现应变集中,在循环载荷下结构处于不安定状态,设计偏于冒险;在管道较短、管道热膨胀量较小时,在分部法中按照一次应力评定设计保守量较大,按照二次应力评定允许结构沿壁厚出现局部塑性变形,但在循环载荷下呈现整体安定的状态。且由于同等温升条件下进行弹性求解,整体法的应力结果均小于分部法,故在管系弹性跟随效应严重时,在整体法中按照二次应力评定,结构仍会由于应变集中产生的大应变在循环载荷下发生失效。
在实际工程应用中,容器-接管连接处在不同载荷条件下发生塑性变形区域的位置和大小不尽相同,因此不能将管道热膨胀量作为应力评定准则适用范围的唯一判据。对于管系热膨胀引起的管系热胀载荷在容器-接管连接处产生的应力评定、一次应力评定和二次应力评定准则的适用范围及条件,仍需要进一步地研究和讨论。
3 结语
(1)在两端固定条件下,管系热膨胀载荷引起的管推力大小与管道长度无关,仅与温升载荷大小有关,但管道系统的热胀量与管道长度有关,热胀量由管道和容器共同吸收。对于串联的两个强度相差较大的结构,允许结构发生塑性变形将会引起弹性跟随效应,进而出现应变集中现象。
(2)分部法与整体法相比,将管推力以机械载荷的形式处理,按一次应力评定。由于忽略了管推力随容器变形的释放效应,其应力计算结果偏大,设计较为保守。
(3)当热膨胀管系-容器系统中的管系热膨胀量较大时,管系对容器管口的弹性跟随效应明显,此时按照一次应力准则对应力进行评定较为安全,按照二次应力评定偏于冒险;管系热膨胀量较小时,按照一次应力评定设计保守量较大,按照二次应力评定允许结构沿壁厚出现局部塑性变形,但在循环载荷下呈现整体安定的状态。在实际工程应用中,对于管系热膨胀引起的管系热胀载荷在容器-接管连接处产生的应力评定、一次应力准则和二次应力准则的适用范围及条件,仍需要进一步地研究、讨论。
