深部采动影响下硬岩巷道围岩稳定性数值模拟研究
2021-05-10代碧波李怀宾张姝婧赵兴东
代碧波 李怀宾 张姝婧 赵兴东
(1.东北大学采矿地压与控制研究中心,辽宁 沈阳 110819;2.金属矿山安全与健康国家重点实验室,安徽 马鞍山 243000)
随着浅部资源的日益枯竭,进入深部高应力区开采资源成为必然趋势。深部开采岩体处于“三高一扰动”的复杂应力环境中,特别对于受采动影响的深部硬岩巷道,巷道围岩常发生层裂、岩爆等灾害事故,造成人员伤亡、设备损坏和生产停滞等。究其原因主要是对采动影响下巷道围岩的力学特性认识不足[1-3],导致不能合理地确定巷道围岩的控制措施。
目前,国内外学者对采动影响下巷道围岩的稳定性进行了大量的研究,例如,贾后省等[4]利用FLAC3D数值模拟方法研究采动叠加应力场分布特征,分析了采动影响条件下巷道围岩的破坏特征与冒顶机理;WACLAWIK等[5]对长壁开采下巷道围岩的应力进行监测,得出随着工作面的推进,围岩应力随之发生改变;WANG等[6]通过钻孔电视监测和声波测试对巷道围岩的破坏情况进行研究,结果表明巷道在采动影响下比在静态压力下围岩破坏区域更大;付玉凯[7]通过数值计算的方法,分析了留巷巷道在临近工作面和本工作面双重采动影响下的围岩应力状态;ABDELLAH等[8]采用统计的方法分析了巷道在采动影响下的稳定性情况。上述研究成果对采动影响下巷道围岩稳定性分析提供了有价值的参考,但对深部采动影响下硬岩巷道稳定性方面的研究相对较少。
红透山铜锌矿现开拓深度1 657 m,开采深度1 257 m,是中国开采最深的有色金属矿山,-767 m中段(埋深1 197 m)13#、14#采场斜坡道在采动影响下,出现大范围的层裂破坏(见图1),给生产带来了严重影响。因此,在深部采动影响下,针对矿山特殊的工程地质和开采条件,研究深部硬岩巷道围岩的稳定性成为红透山铜锌矿深部开采的重点课题。针对上述实际情况,以红透山铜锌矿-767 m中段13#、14#采场斜坡道为研究对象,采用数值模拟方法分析开采过程中巷道围岩的应力、塑性区和位移变化规律,为采动影响下巷道稳定性分析和支护设计提供了重要的理论依据。

1 工程地质
红透山铜锌矿床位于浑河大断裂带上盘,矿体上盘为黑云斜长片麻岩、下盘为角闪斜长片麻岩。矿床总体走向近东西,倾向南东,倾角在70°~80°之间,矿体平均厚20 m。目前红透山铜锌矿主要采用上向水平分层充填采矿法,矿房垂直高度60 m,每分层开采高度3 m,采用尾砂胶结充填;-767 m中段13#、14#采场斜坡道巷道断面尺寸3.0 m×2.8 m(宽×高),为四分之一三心拱巷道,采场与斜坡道位置关系见图2。

利用测线法对研究区域岩体结构面进行调查分析可知,其岩体结构面分布情况见表1。根据现场调查和室内岩石力学实验,采用RMR和Q方法对岩体质量进行分级(见表2),岩体质量一般~好,最后基于Hoke-Brown强度准则估算岩体力学参数(见表3)。



2 采动影响下围岩稳定性数值分析
2.1 开采方案
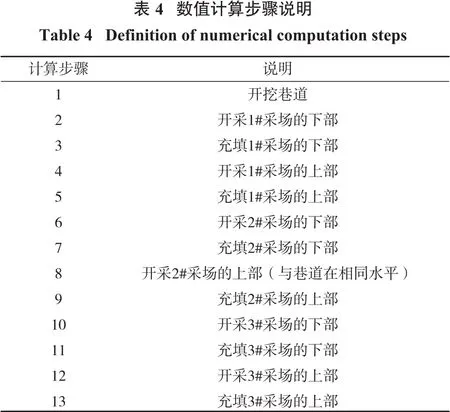
为了研究采动影响下斜坡道围岩的稳定性,考虑13#、14#采场斜坡道同中段的采场以及上下两个中段采场的影响,为了简化计算,每个采场分两步开采,总体开采次序为从下到上,在模型计算中,具体的计算步骤为模拟开采和充填的次序(见表4)。采用FLAC3D软件分析采动影响下巷道围岩的应力、塑性区和位移的变化规律。
2.2 数值模型建立
模型尺寸为1 000 m×20 m×1 260 m(长×宽×高),划分271 520个单元,如图3所示,考虑到计算精度的问题,对巷道位置处网格进行加密处理,矿体倾角为70°,厚度20 m。模型边界采用位移约束,水平方向限制x和y方向的位移,模型底边限制x、y和z方向的位移,模型上边界施加覆岩自重的应力,约为15 MPa,模拟采用Mohr-Coulomb强度准则。

2.3 模拟结果分析
2.3.1 主应力演化过程分析
为了得到围岩主应力随开采的演化过程,在斜坡道围岩的左帮、拱肩和顶板处沿径向方向10 m内每隔0.2 m布置1个测点,监测该点处的主应力值。为了便于观察,在此设定压应力为正。
(1)帮部主应力。根据以上模型,提取围岩一监测断面左帮中点处不同深度测点的主应力值(见图4)。可以看出,最大主应力值在帮壁附近相对较小,随着径向深度的增加,最大主应力值先增加后减小,深度在距离帮壁2倍巷道宽度时,该点的主应力值趋于稳定;在距离帮壁0.5 m范围内最小主应力值较小,围岩易发生σ3<5 MPa时的张拉破坏,随着径向深度的增加,最小主应力值增大,围岩易发生σ3>5 MPa时的剪切破坏[10];随着开采的进行,最大主应力峰值先增加后减小,这主要是由于开采至巷道水平附近时,在巷道附近形成应力集中区,开采超过巷道水平后,应力集中区随之发生转移,在巷道靠近采场侧应力开始释放;帮壁处最大主应力和最小主应力值均逐渐减小。

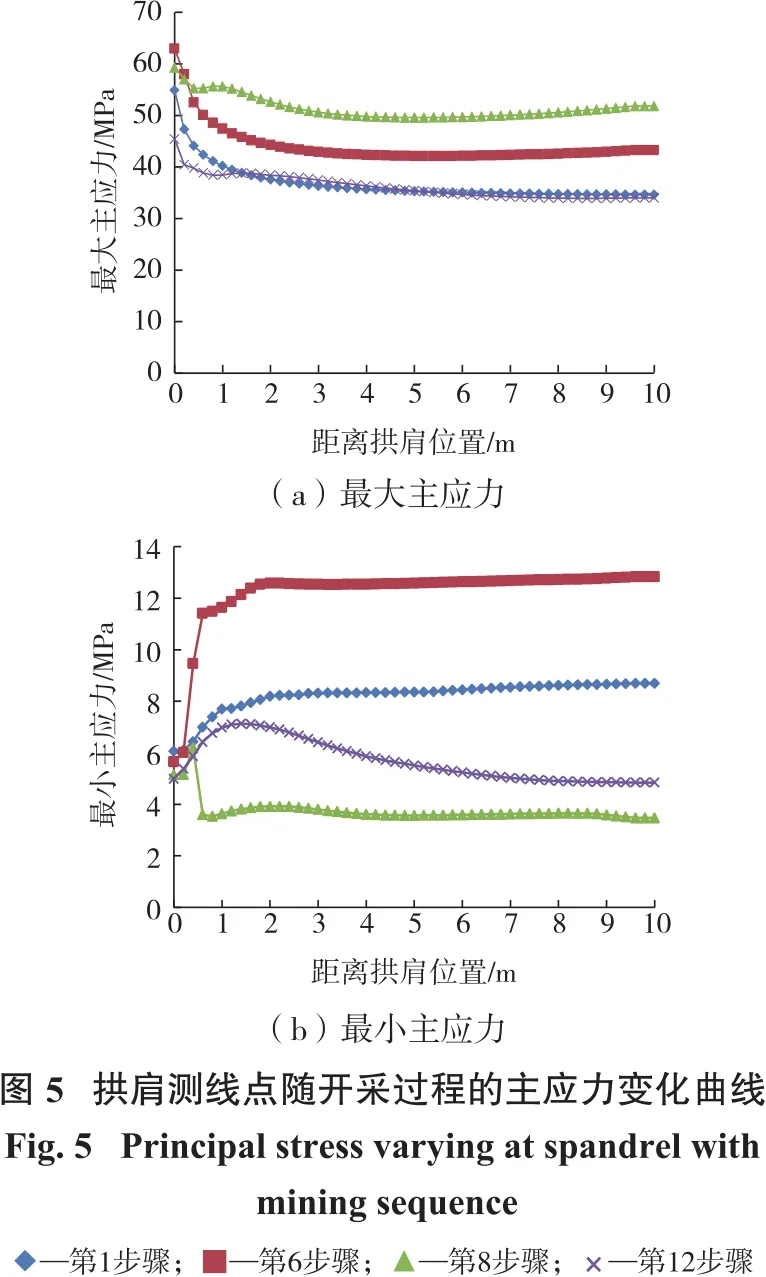
(2)拱肩主应力。提取巷道拱肩不同深度测点的主应力值(见图5)。可以看出,最大主应力值在拱肩处出现应力集中,随着径向深度的增加,最大主应力值逐渐减小,深度在距离拱肩2倍巷道宽度时,该点的主应力值趋于稳定;最小主应力在拱肩附近就达到较大值,围岩易发生σ3>5 MPa时的剪切破坏[10];随着开采的进行,最大主应力峰值先增加后减小,这主要是由于开采至巷道水平附近时,在巷道附近形成应力集中区,开采超过巷道水平后,应力集中区随之发生转移,在巷道靠近采场侧应力开始释放。
(3)顶板主应力。提取巷道顶板中点处不同深度测点的主应力值(见图6)。可以看出,随着径向深度的增加,最大主应力值逐渐增加,深度在距离顶板3倍巷道宽度时,该点的主应力值趋于稳定;在距离顶板0.5 m范围内最小主应力值较小,围岩易发生σ3<5 MPa时的张拉破坏,随着径向深度的增加,最小主应力值增大,围岩易发生σ3>5 MPa时的剪切破坏[10];随着开采的进行,最大主应力峰值先增加后减小,这主要是由于开采至巷道水平附近时,在巷道附近形成应力集中区,开采超过巷道水平后,应力集中区随之发生转移,在巷道靠近采场侧应力开始释放;当计算至第8步骤时,顶板出现2 MPa的拉应力,大于岩体的抗拉强度;在第12步骤时,顶板处最小主应力值接近0 MPa的深度约为1 m,此时围岩处于双向应力状态。
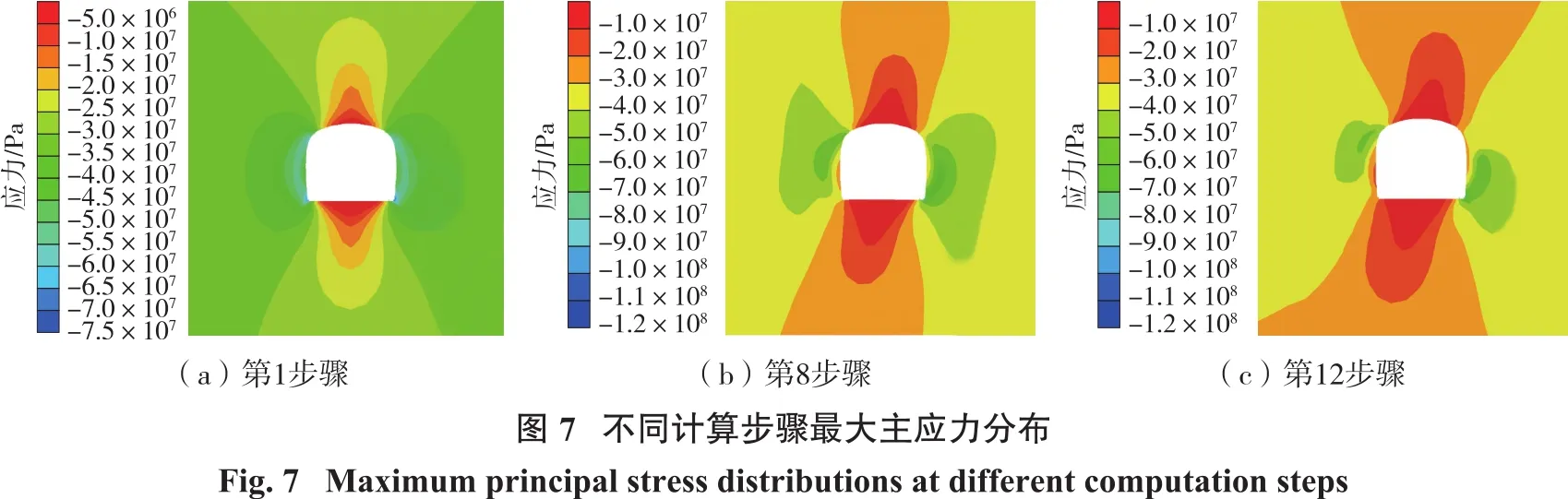
(4)应力集中位置分析。为了进一步确定开采后主应力的变化情况,图7给出了第1步骤、第8步骤和第12步骤最大主应力集中点位置。结果表明:随着开采的进行,应力集中区位置沿顺时针方向转动;转动角度达20°左右,应力集中区位置的转动导致巷道塑性区以及锚杆受力的变化,增加了巷道的不稳定性。
2.3.2 塑性区演化过程分析
随着开采的进行,巷道围岩的塑性区变化如图8所示,在第1~第6步骤时(见图8(a)和图8(b)),巷道围岩塑性区较小,塑性区范围几乎没有变化,最大塑性区出现在底板,范围为0.8 m;当开采至与巷道相同水平时(见图8(c)),巷道围岩塑性区范围明显增大,最大塑性区出现在底板,范围为5.0 m;随着采场的持续开采,两帮及底板塑性区范围变化不大,在第12步骤时,靠近采场侧,顶板塑性区增加至6.5 m,并且围岩塑性区呈不对称分布,对于3.0 m×2.8 m三心拱巷道,设计支护的锚杆长度一般为2.0~2.5 m,塑性区远远超出正常的支护范围,所以对受开采影响的巷道进行支护时,必须充分考虑开采的影响。开采结束后,巷道围岩的塑性区具有以下的变化规律,巷道左帮(靠近采场侧)从0.35 m(第1步骤)增加至0.6 m(第12步骤);巷道右帮(远离采场侧)从0.35 m(第1步骤)增加至0.4 m(第12步骤);底板从0.8 m(第1步骤)增加至5.4 m(第12步骤);顶板从0.2 m(第1步骤)增加至6.5 m(第12步骤)。

2.3.3 位移变化规律分析
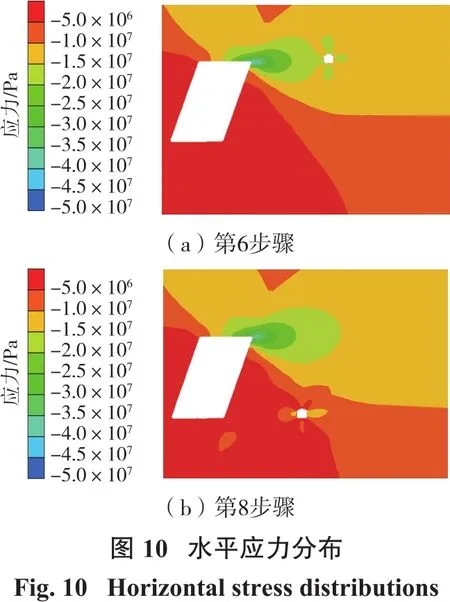
由于沿着巷道帮壁位移不均匀分布,一般情况下,在帮壁的中间位置比较接近最大位移变化值,选取帮壁的中点进行说明,图9给出了随着开采的进行,巷道两帮位移的变化情况,正值表示远离采场方向,负值表示靠近采场方向。巷道左帮先向远离采场方向移动(第1~第7步骤),然后向靠近采场方向移动(第8~第13步骤),从1.9 mm减小至-33.3 mm;巷道右帮在第1步骤时向采场方向移动,然后开始向远离采场方向移动(第2~第7步骤),最后同左帮一起向靠近采场方向移动(第8~第13步骤);从-1.4 mm减小至-31.5 mm。巷道两帮总体表现出先向远离采场方向移动,然后向靠近采场方向移动的规律,这主要是由于,在第1~第7步骤,尤其在第6~第7步骤后,在采场的右上角出现水平应力集中(见图10(a)),然而在巷道右侧的整体水平应力值没有明显的变化,导致巷道整体向远离采场方向移动;当开采超过巷道相同水平后,巷道左侧水平应力得到较大的释放(见图10(b)),然而在巷道右侧的整体水平应力值没有明显的变化,导致巷道整体向靠近采场方向移动。

巷道顶底板采用上述方式,选取中点进行说明,负值表示下沉量。巷道开挖后,顶板出现-4.8 mm的位移,第2~第5步骤顶板下沉量逐渐减小,在第6步骤时,顶板位移开始变为正值,这是由于采场开挖后,在巷道左侧产生水平方向应力集中(见图10(a)),导致顶板下沉量减小;计算至第8步骤之后,顶板向上移动快速增加,这主要是由于随着开采的进行,垂直应力分量逐渐减小(见图11),顶板位移从-4.8 mm增大至61.5 mm。随着开采的进行,巷道底板隆起量持续增加,从5.9 mm增加至78.8 mm。开采结束后,巷道整体向靠近采场方向倾斜移动(见图12)。


3 结 论
(1)巷道开挖后,在距离帮壁和顶板0.5 m和1.0 m范围内最小主应力值较小,围岩易发生张拉破坏,而最小主应力在斜坡道拱肩附近就达到较大值,围岩易发生剪切破坏;随着径向深度的增加,帮壁处最大主应力值先增加后减小;拱肩处最大主应力值逐渐减小,顶板处最大主应力值逐渐增加,最终趋于稳定。
(2)随着开采的进行,最大主应力峰值呈现先增加后减小的规律;最大主应力集中区沿着顺时针方向转动,转动角度20°左右;围岩塑性区逐渐变为蝶形,并呈不对称分布;顶板先下沉后向上移动,从-4.8 mm增大至61.5 mm;巷道底板隆起量持续增加,从5.9 mm增加至78.8 mm;斜坡道两帮总体表现出先向远离采场方向移动,然后向靠近采场方向移动的规律,左帮从1.9 mm减小至-33.3 mm,右帮从-1.4 mm减小至-31.5 mm;开采结束后,斜坡道整体向靠近采场方向倾斜移动。
(3)对比所有计算步骤表明:在开采至斜坡道相同水平时,开采对斜坡道围岩的稳定性的影响较显著,此时斜坡道围岩出现蝶形塑性区,帮壁在水平方向上,从向远离采场方向移动转向靠近采场方向移动,顶板向上移动开始加剧。
