下向分层进路式胶结充填法采场稳定性判断方法及应用

张志贵 谭宝会 钟 敏 陈星明 朱 强 李明润

（西南科技大学环境与资源学院，四川 绵阳 621010）

下向分层胶结充填采矿法是厚大高应力破碎矿体较常采用的一种采矿方法［1］。由于其在提高矿石回收效果、控制采场地压、维持采场稳定和控制地表沉降及塌陷方面的良好效果，更是受到高价值矿石以及地表需要严格保护的矿山重视和欢迎，可以说，下向分层胶结充填采矿法已经成为这类矿山的主要采矿方法［2-4］。一般来讲，下向分层进路式胶结充填采矿法设计上通常采用采一充一的生产组织方式，但是为了便于生产组织以及提高产量，大多矿山实际上采取的是隔一采一的多进路同时作业方式，即几条间隔但相邻的进路在同时回采，待回采完成后再进行集中充填的生产组织方式。因而采场在一定时间内形成了以胶结充填体为顶板的多个相邻非连续采空区，由此带来了胶结充填法采场稳定性的问题。此外，在采用下向分层进路式胶结充填法回采急倾斜厚大矿体时，生产矿山一般会采取分区回采的作业模式，即同一开采分层内有若干区域同时进行回采，在每一个回采区域内均是几条进路同时回采然后再集中充填，一定时间内形成了更为复杂的多区域相邻非连续采空区，不仅采场稳定性问题更加复杂，采场失稳的风险也显著增加。

目前尚无有效成熟的方法对这种具有相邻非连续采空区特征的胶结充填法采场稳定性进行分析和判断，对采场稳定性控制缺乏有效指导，难以防止可能造成的采场稳定性风险，已有生产矿山发生了大面积胶结充填体垮塌事故［5］。因此，有必要就下向分层进路式胶结充填法采场稳定性分析及判断方法进行研究。

1 下向分层进路式胶结充填采矿法作业方式及特征

下向分层胶结充填采矿法将矿体在延深方向划分为中段（或阶段），中段再划分为分段或直接划分为回采分层，分层内再进一步划分为最为基本的回采单元即回采分条或回采进路，采矿形成的采空区需要采用胶结充填料及时进行充填。就其回采顺序来看，不论是中段、分段还是分层，都是采取从上到下的回采顺序。而分层内回采基本单元（回采进路）采取隔一采一的方式保持多条进路同时回采，此外厚大矿体通常会采取多区域同时回采的工作方式。图1为典型的下向分层进路式胶结充填采矿法采场结构示意图。

需要指出的是，正是由于完全的自上而下的回采顺序，使得下向分层胶结充填法具有不同于其他充填采矿法的技术特征，即胶结充填体为采场的直接顶板，采场稳定性问题主要是胶结充填体的稳定性问题。同时，不同于其他采矿方法的采空区，其采场采空区呈现为多个间隔存在的长条形采空区形态，且采空区之间的间隔（即间柱宽度）较小，一般仅为4～6 m左右，间柱的稳定性也会影响到采场的稳定性。

2 地下采场采空区稳定性分析与判定方法

地下采场采空区的稳定性分析与判断可以通过理论计算［6］、数值模拟［7］、Mathews稳定图法［8］以及现场监测［9］等手段来进行。但是，就实际工程应用角度看，理论计算可操作性强，其结果也往往能够起到一定的指导作用，但当地质条件较为复杂、岩性变化较大时则无法准确预测；数值模拟具有经济易行等优点，目前应用最为广泛也最具前景，但其结果易受人为主观解释的影响；而现场监测手段通常只能对影响采场稳定性进行事中及事后被动监测，对采矿生产指导的及时性较差，且费时费力，投入较大。

虽然Mathews稳定图法是目前接受度较高、应用较普遍的地下空间稳定性分析与判断方法，但该方法需要确定岩体质量指标修正值、岩石应力系数、节理方位系数、空区重力调整系数以及稳定数和空区形状系数等多个复杂且较难以获取的参数，使用起来仍显复杂和繁琐。尽管如此，Mathews稳定图法主要是对单一连续的采空区稳定性进行评价分析，而对于类似下向分层进路式胶结充填法采矿形成的距离较近、相互影响的采空区群落的稳定性问题，目前还没有一个明确而有效的分析及判断方法。因此，有必要探索一些更为简便、实用且及时有效的分析方法，对地下采场空间包括相互影响的多个地下采场空间的稳定性进行事前评估和判断，实现对生产安全进行及时有效的指导。

2.1 单一连续采空区稳定性判定方法

地下采场采空区的稳定性分析和判断，可以根据其是否符合发生自然冒落的条件来进行。目前国内对单一连续采空区稳定性判断使用较多的方法是由东北大学任凤玉教授提出的诱导冒落理论［10］。该理论考虑了采场埋深、矿岩稳固性以及采空区形态等诸多因素对采空区稳定性的影响，主要通过分析采空区的跨度及面积是否达到其临界冒落跨度及面积来判断采空区的稳定状态。该方法具有简单、明了、计算参数容易获取等优点，且经众多实践案例检验，证明其具有较好的适用性。在诱导冒落理论中，采空区临界冒落半跨度计算公式如下：

式中，Lc为采空区临界冒落半跨度，m；h为采空区高度，m；Tc为顶板岩体极限抗压强度，t/m2（平面问题）；γ为顶板岩体容重，t/m3；H为空区顶板埋深，m。

采空区临界冒落等价圆面积计算公式如下：

需要注意的是，公式（2）中所计算的采空区临界冒落等价圆面积是指采空区达到临界冒落的有效面积，而并非简单的几何尺寸面积，临界冒落半跨度相应的也是冒落等价圆的半径。也就是说，当地下采空区的跨度及面积达到发生自然冒落的跨度及暴露面积时，可认为采场处于不稳定状态；反之，则采场处于稳定状态。然而，地下采矿形成的采空区形态通常是较为复杂且不规则的，而采空区形态会在很大程度上影响到采空区的稳定性，例如对下向分层进路式胶结充填法而言，单个进路回采所形成的采空区通常长度较大而宽度较小，此时就可能出现单个进路采空区的实际暴露面积大于理论计算出的临界冒落等价圆的面积，但进路采空区实际跨度却小于理论计算的临界冒落半跨度的情况，此时就难以对单个进路采空区的稳定性做出判断。因此，在利用诱导冒落理论分析判断采场稳定性时，进行比较的采空区面积应该是能导致采空区发生冒落的有效暴露面积而不是空区实际几何暴露面积。然而，如何将采空区实际暴露面积转换为有效暴露面积，目前尚缺乏一个合理的解决方案。

2.2 相邻非连续采空区稳定性判定方法

对于下向分层进路式回采的胶结充填采矿法矿山来讲，由于产量或管理等因素的影响，实际生产中通常都是3～5条甚至更多条进路采完后才会进行集中充填，形成了间隔很小但面积很大的相邻非连续采空区。同时，对于厚大矿体条件，生产矿山通常会实行多区域回采，每一回采区域范围内也是几条进路采完后再集中充填，形成了更为复杂的多区域相邻非连续采空区，而且这些相邻非连续采空区形态以及面积还会随着采充工作不断推进而不断变化。可以肯定的是，由于进路之间的间柱宽度一般较小，承载力及稳定性较差，相邻采空区之间的稳定性必然会相互影响。显然，多区域的大面积相邻非连续采空区的出现，将使采场失稳的风险显著增大，本文中将出现在采场中的大面积相邻非连续采空区称之为“稳定风险区”。

然而，目前对于下向分层进路式胶结充填法采矿形成的相邻非连续采空区的稳定性分析与判断还没有一个比较行之有效的方法。鉴于此，本文提出了一种“等效采空区法”来对其进行定量分析和判断，所谓“等效采空区法”是将采场内相邻但不连续的采空区面积转换或折算为等效的连续采空区面积进而定量分析和判断其稳定性的方法。所谓的“等效采空区”是指考虑了相邻采空区间柱宽度以及采空区形态（长宽比）等因素后，可视为能代表采场相邻非连续采空区稳定状态的连续采空区。

根据生产矿山了解到的实际情况，下向分层胶结充填法的冒落一般只发生在矿体范围内的采空区，故主要考虑矿体内以胶结充填体为顶板的采空区稳定性问题。同时，考虑采空区形状因素，将长宽比等于1的方形或圆形视为最容易冒落的形状，其他形状则应进行相应的折减。此外，相邻采空区之间矿柱的宽度也是影响采空区稳定性的关键因素之一，必须予以考虑。

这样，下向分层进路式胶结充填法采场中相邻非连续采空区（“稳定风险区”）的等效采空区暴露面积可以按照下式进行计算：

式中，Se为采场内某一“稳定风险区”的等效采空区暴露面积，m2；St为采场内某一“稳定风险区”中相邻非连续采空区总面积，m2；d为间柱宽度，m，若相邻采空区之间间柱宽度不一致，按最小宽度取值；α为采场内某一“稳定风险区”相邻非连续采空区形态系数，采用能包含该区域全部相邻非连续采空区的椭圆长短轴之比。

若通过公式（3）计算出的“稳定风险区”的等效采空区面积Se大于公式（2）计算出的采空区临界冒落等价圆面积Sc，则采场处于不稳定状态；反之，则采场处于稳定状态。对于采场内有多个开采区域的矿山来讲，可首先在采场中圈定出多个“稳定风险区”，然后再分别计算其等效采空区面积并判断其稳定性。

其实，“等效采空区法”既可以应用于分析和判断下向分层进路式胶结充填法采场的稳定性，也可以应用于其他类型充填法采场甚至是崩落法采场的稳定性分析，这也包括具有多个相邻非连续（条柱间隔）采空区或单一采空区特征的采场稳定性分析。但是，其他类型充填法以及崩落法采场的空区可能具有与下向分层进路式胶结充填法不同的形态特点，比如空区间柱宽度可能要远大于下向分层进路式充填法采空进路之间的间柱宽度，此时就需要恰当定义“相邻非连续采空区”并合理划定“稳定风险区”。根据受力分析［11］，当2个相邻采空区相距较近、间柱宽度较小时（见图2（a）所示），各空区开挖引发的应力集中会在间柱上发生叠加，若间柱发生破坏则相邻采空区均有可能发生失稳，此时相邻采空区之间的稳定性是相互关联的；而当相邻采空区距离较远、间柱宽度较大时（见图2（b）所示），各空区开挖引发的应力集中不在间柱上发生叠加，此时间柱不易受到破坏，采场的稳定性主要取决于单个采空区顶板的稳定性，相邻采空区之间的稳定性相互关联度不大。

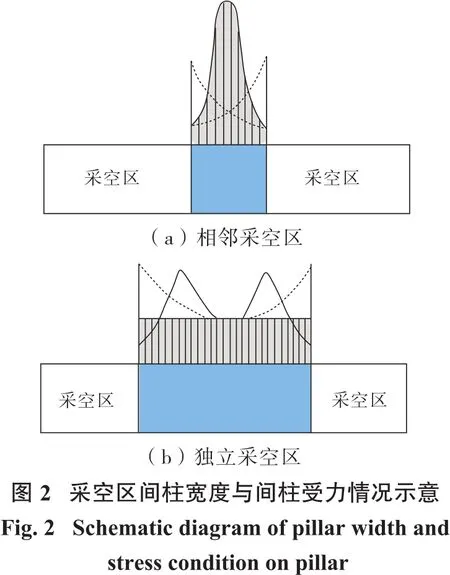
因此，可以将采空区之间间柱出现显著应力叠加的采空区定义为相邻采空区；而采空区之间间柱上基本没有出现应力叠加的采空区定义为独立采空区。这样，将定义为相邻采空区的区域划定为“稳定风险区”，按照公式（3）计算其等效采空区面积Se并根据公式（2）计算临界冒落等价圆面积Sc，最后通过对比二者大小来判断采场稳定性。

至于定义为独立采空区的区域，其采场稳定性的大小则主要取决于采空区面积大小及形状。由于根据诱导冒落理论计算出的是采空区临界冒落等价圆半径以及等价圆面积，不能直接对采场采空区稳定性进行分析和判断。因此，仍可考虑采用“等效采空区法”来对独立采空区的稳定性进行分析。不过，此时“等效采空区”面积的转换就不再考虑间柱宽度因素而只需要考虑采空区形状因素。具体的方法是，根据独立采空区的实际形态，对于规则的矩形采空区直接采用其长宽比，而对于不规则形态的采空区，则需要找出最符合采空区形态的椭圆并确定其长短轴之比，计算“等效采空区”面积的公式可以简化为：

式中，Si为独立采空区实际暴露面积，m2；α为独立采空区形态系数，矩形采空区直接采用其长宽比，不规则形态采空区采用最符合该采空区形态的椭圆长短轴之比。

显然，通过恰当定义相邻采空区并合理划定稳定风险区，将“等效采空区法”这种简便有效的方法扩大应用至其他类型充填法甚至崩落法采场稳定性分析与评价中，包括对多个采空区和单个采空区的采场稳定性评价与分析，可以解决目前地下矿山采场稳定性分析与评价缺乏简便有效方法的困境。

3 下向分层进路式胶结充填采矿法采场稳定性判定与分析

某矿为一大型有色金属矿山，地表以下100 m见矿，矿体赋存标高为1 058～1 671 m，走向北27°西，倾向南西，倾角 70°～80°，厚度 28～200 m，沿走向全长463 m，矿体及围岩均较破碎。由于矿石价值较高，加之矿区构造应力大且矿岩破碎，矿山采用下向水平分层进路式胶结充填法进行开采，回采进路宽度为6 m，高度为5 m，进路之间的间柱宽度4 m。矿山选择棒磨砂为充填骨料，胶凝材料选择425#普通硅酸盐水泥，充填料浆灰砂比为1∶4，浓度为78%，胶结充填体的强度要求为5 MPa。为扩大产能，矿山采用上、下双中段同时作业的回采模式，年产能可达165万t。图3为矿山在2016年3月时的双中段回采状态。

2016年3月13日凌晨03:30时，矿山上部中段1 613 m充填分层的工区值班人员发现7行勘探线2号分层道33号进路两帮充填体明显变形开裂，并伴有异响，采区立即组织人员及设备撤离。当日06:40时该分层采场发生大规模失稳，冒落的胶结充填体散块将5行、6行、7行穿脉分层道堵死，见图4所示。尽管本次采场垮塌事故未造成人员伤亡，但直接导致上部中段的采矿作业全面中止，给矿山带来了巨大的经济损失。

依据公式（1）和公式（2）计算可知，该矿1 613 m充填分层采场发生临界冒落的空区半跨度为10.8 m，临界冒落等价圆面积为366 m2。而矿山回采进路宽度为6 m，进路长度一般为40～50 m，单条进路对应最大采空区暴露面积在300 m2以内，因而如果从单个进路回采形成的采空区跨度和暴露面积来看，胶结充填采场是稳定的。也就是说，采场如果能按照“采一充一”工作方式来进行的话，采场便能保持稳定，然而采场中通常在某一集中区域有多条相邻进路在集中采矿，采矿结束后才统一充填，此时就需要采用“等效采空区法”来对采场稳定性进行判别。1 613 m充填分层采场顶板垮塌时的采场回采状态如图5所示。由图5可见，该分层垮塌时采场中存在3个“稳定风险区”，即图5中的A、B、C3个区域，其中发生垮塌的部位为C区域，A、B区域保持稳定。为验证本文所提出的“等效采空区法”的有效性和可靠性，采用“等效采空区法”对1 613 m充填分层中3个“稳定风险区”的稳定状态进行分析判别，并与实际情况进行对比验证。

先利用能包含“稳定风险区”全部相邻非连续采空区的椭圆将上述3个“稳定风险区”的具体区域圈定，同时测量出椭圆的长半轴及短半轴的长度，并分别测量出上述3个“稳定风险区”中包含的采空区实际暴露面积，再利用公式（3）计算出各“稳定风险区”的等效采空区暴露面积，最后与公式（2）计算出的该充填分层的临界冒落等价圆面积相比较进行判断，相关计算及分析结果见表1。

由计算结果可以看出，1 613 m充填分层中编号为C的“稳定风险区”计算出的等效采空区暴露面积已达580 m2，远超过该分层采空区临界冒落等价圆面积366 m2，因而该区域属于不稳定区域，极有可能发生采场大面积失稳事故，事实上采场垮塌事故也确发生在该区域。而A、B两个“稳定风险区”的等效采空区暴露面积分别为162 m2和100 m2，小于该分层采空区临界冒落等价圆面积，故应该处于稳定状态，而事实上这2个区域也的确处于稳定状态。可以看出，1 613 m充填分层各回采区域的实际稳定情况与计算结果作出的分析判断非常吻合，说明采用“等效采空区法”来计算和分析具有相邻非连续采空区特点的下向分层进路式胶结充填法采场稳定性的方法是可行的，也是有效的。

为进一步验证“等效采空区法”的有效性，持续采用该方法对矿山下部中段1 494 m充填分层的采矿情况进行跟踪并进行稳定性判断。图6给出了1 494 m充填分层在2018年9月时的开采状态，根据当时采场开采状态，可以在该分层划分出4个具有相邻采空区特征的“稳定风险区”。

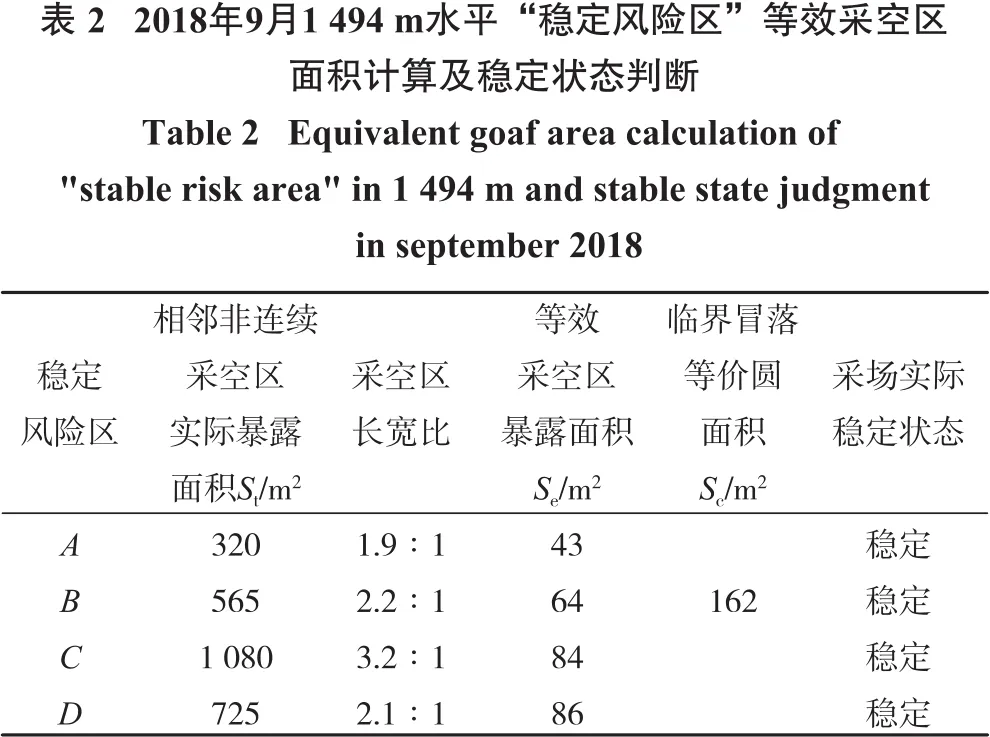
圈定好“稳定风险区”后，采用“等效采空区法”对各“稳定风险区”进行分析判断，相关计算数据列于表2之中。由计算结果可以看出，1 494 m充填分层的4个“稳定风险区”的等效采空区暴露面积为43～86 m2，低于该分层采空区的临界冒落等价圆面积162 m2。因此，可以认为在该回采状态下1 494 m充填采场不仅整体是稳定的，各回采区域也是稳定的，该结论与1 494 m充填采场在2018年9月时的实际状况是吻合的。

经过半年回采后，再次采用“等效采空区法”对1 494 m充填分层的稳定状态进行分析判断。图7为1 494 m充填分层在2019年3月时的开采状态，此时在采场中可以划分出5个具有相邻非连续采空区特征的“稳定风险区”。

同样的，采用“等效采空区法”对2019年3月时1 494 m充填分层的各“稳定风险区”进行分析判断，计算数据及分析结果列于表3之中。根据计算结果可以看出，经过近半年左右的回采，1 494 m充填分层部分回采区域（区域C）出现了等效采空区面积大于该分层临界冒落等价圆面积的情况，表明该区域已经具有潜在冒落风险，属于不稳定区域，需要减缓回采速度、加快充填进度，以减少采空区暴露面积。同时，E区域的等效采空区面积也趋近于临界冒落等价圆面积，因此该区域也需要调整采充进度，减少采空区面积，确保采场稳定。随后，矿山及时根据本次计算结果对1 494 m分层的采充进度进行了必要调整，在后续生产中采场保持稳定与安全状态。

以上实例分析结果表明，对于具有相邻非连续采空区特点的下向分层进路式胶结充填矿法，采用“等效采空区法”对其采场稳定性进行分析和判断是可行的，也是有效的，该方法可以同时实现对胶结充填采场稳定状态的定量分析和定性判断，而且在操作上更简便易行，便于及时掌控采场的采充进度，确保采场作业安全，对实际生产更具指导性。

4 结 论

针对下向分层进路式胶结充填法采场稳定性分析及判别过程复杂、繁琐、难度大的问题提出了等效采空区法，致力于以一种简便有效的方法来解决下向分层进路式胶结充填法采场稳定性的分析与判断问题，得到如下结论：

（1）等效采空区法综合考虑了采场地压、胶结充填体强度、间柱宽度以及采空区形态等多重因素对采场稳定性的影响，不仅能实现相邻非连续采空区稳定性的定量计算与分析，更能反映出采场的实际稳定状态，且具有简单、明了、操作性好、针对性强等一系列优点，实践证明这种方法有效可行。

（2）通过恰当定义相邻采空区并合理划定稳定风险区，可以将等效采空区法这种简便有效的方法扩大应用至其他类型充填法甚至崩落法采场稳定性分析与评价中，包括对多个相邻非连续采空区（条柱间隔）和单个采空区的采场稳定性评价与分析，解决了目前地下矿山采场稳定性分析与评价缺乏简便有效方法的困境。

（3）作为主要针对下向分层进路式胶结充填法采场稳定性分析与判断问题而提出的解决方法，等效采空区法也存在一定的局限性。首先，采空区主要针对的是条柱间隔的非连续相邻采空区，不包括空场法点柱分布的连续采空区；同时，当间柱尺寸较大时，有可能出现相邻非连续采空区计算的等效采空区暴露面积小于按照单个独立采空区计算的等效采空区暴露面积的情况，此时应按照单个独立采空区进行分析和判断。总之，等效采空区法扩大应用的可行性及有效性还有待通过进一步的理论研究和实际工程应用进行必要的验证和完善。