矩形采场支护作用下围岩周边应力复变函数解析解
2021-05-10李元辉刘明飞李坤蒙熊志朋
李元辉 刘明飞 李坤蒙 熊志朋
(深部金属矿山安全开采教育部重点实验室,辽宁 沈阳 110819)
地下矿体的开采必然打破围岩原有的应力平衡状态,导致其应力场重新分布[1]。尤其对于深部采场,高应力作用下围岩稳定性较差,极易诱发顶板冒落、垮塌等地压灾害。为了控制采场围岩的稳定性,通常借助留设原岩矿柱、人工支柱或锚网、锚喷等方式改善围岩的应力状态,确保回采过程中采场的安全作业条件。采场回采过程中,准确掌握支护作用下围岩应力状态是采场地压控制和支护参数优化的理论基础,具有十分重要的工程指导意义。
针对圆形孔洞周边的应力和变形问题,岩石力学及弹性力学已经给出了较为完善的解析解,而对于矩形开挖周边的应力变形问题仍处于研究阶段[2]。上个世纪前苏联学者Muskhelishvili[3]首次将复变函数应用于弹性力学问题之中,为解决非圆形巷道或硐室边界方面的问题提供了新思路。鉴于复变函数具有保角变换功能,能够将物理平面上复杂形状的边界问题转换成圆形形状的简单边界求解,因此弹性力学中的复变函数法对于解决非圆形孔口问题具有其独特的优越性[4]。朱大勇等[5]提出了对不同形状的孔口通过保角变换得到映射函数的方法;赵凯等[6]介绍了一种通过不断迭代循环的手段求解矩形硐室映射函数的新方法,并通过算例验证了这种方法具有很高的实用性;Sharma等[7]分析了圆形、椭圆形、三角形和四边形硐室围岩的应力分布,提出加载角度和拐角半径是影响应力集中的关键因素;陈斌[8]系统地给出并验证了复变函数求解双向均布载荷孔口问题的一般步骤;姜学淼[9]揭示了不同宽高比的矩形巷道围岩边界不同角度的应力分布规律;施高萍等[10]计算得出了原岩垂直和水平应力分量单独作用的顶板和侧帮中点的应力集中系数;Zhao等[11]采用复变函数的保角变换方法研究了方形隧道围岩的应力分布规律,研究表明在45°角位置附近即方形隧道的拐角处应力集中较大,侧压系数在0.8~1.2范围内隧道边界不会出现拉应力;吕情绪等[12]根据复变函数的理论,通过计算求出采场在保角变换取三次项的情况下的极限长高比;Gao等[13]通过复变函数计算,给出了矩形巷道孔口周边不同角度处的应力和位移的解析解。Wang等[14]讨论了各向异性全滑移接触隧道的解析解,通过对边界条件的检验和数值模拟的比较,验证了解析解具有较高的精确性。
纵观目前的研究,基于弹性力学理论,国内外学者研究了不同形状断面巷道或硐室围岩周边的应力分布复变函数解,揭示了未支护条件下采场围岩周边的应力分布规律。然而,在实际采场回采过程中,必须采取一定的支护措施来控制围岩的稳定性,目前运用复变函数理论求解支护作用下矩形采场围岩周边应力状态问题鲜有研究,无法为现场工程支护设计提供理论依据。鉴于此,本项目旨在建立矩形采场围岩应力分布的复变函数计算模型,研究在不同支护阻力作用下采场围岩周边应力的理论计算公式。同时,借助数值模拟方法对理论解析解进行验证,最终揭示支护作用下采动围岩周边的应力状态,为采场稳定性控制和支护参数确定提供理论基础。
1 矩形采场支护作用下围岩应力解析力学模型
1.1 力学模型
为了对支护作用下的矩形采场围岩应力分布状态进行计算,首先需建立求解的理论力学模型,如图1所示。

具体假设条件:
(1)采场形状位于模型中央,整体为规则的矩形,其断面宽为2a,高为2b,且断面尺寸远远小于模型整体尺寸,可将应力场的求解简化成无限域的孔口问题[15]。
(2)只考虑自重产生的初始应力场,且假设采场埋深较大,可忽略采场附近由于重力引起的梯度效应,故认为模型受到竖直方向均匀的远场应力σv和水平方向均匀的远场应力σh=λσv,式中λ为侧压力系数。
(3)围岩为均质、各向同性的连续介质,只发生弹性变形。
(4)采场内壁受到均匀的垂直和水平支护阻力,且大小均为f。
1.2 解析原理
如图2所示,矩形采场支护作用下围岩周边应力计算可以简化成弹性力学中的平面孔口问题,采场同时受到竖直方向均匀的远场应力σv和水平方向均匀的远场应力σh=λσv。此外,孔口内壁由大小相等的垂直和水平均布支护阻力f控制。计算支护作用下矩形采场围岩周边应力大小可拆分成两部分讨论,对于仅存在远场应力且孔口内壁不支护条件下的围岩应力解析,研究者已进行了比较深入研究[5-14]。本项目基于已有的研究进行拓展和延伸,计算孔口内壁支护作用下的围岩周边应力,利用复变函数的保角变换功能,将物理平面上复杂矩形形状转化为简单的单位圆形状进行分析,推导计算出相应复势函数和复变解析量,同时,分别求出两种不同情况围岩应力的解析特解,再将其合成叠加,进而求得围岩应力分量的解析解。最后,借助数值模拟的手段,求出矩形采场在支护条件下围岩周边应力数值模拟解,进一步验证解析法的正确性。

2 矩形采场围岩周边应力理论解
2.1 复变函数保角变换
为了利用复变函数理论求解矩形采场围岩周边的应力,必须采用保角变换的手段将物理平面上的矩形区域映射到像平面上的圆形区域。对于映射函数的选取,包括诸多解法[16-19],如 Schwarz-Christoffel公式的混合罚函数法、三角形插值法、Мeлентьев法、多角形逼近法、Verruijt共形映射函数、Laurent级数展开的复合形法等,本项目选取最后一种进行求解,该方法便于理解且计算简便,同时具有较高的适用性和精确度。
Laurent级数展开的复合形法是将矩形弹性体在物理平面(问题的实际区域,也叫z平面)上所占区域转化成像平面上的中心单位圆区域(也叫ζ平面),其中物理平面上矩形采场右边界中点(a,0)、顶板中点(0,b)和右顶角(a,b)分别与像平面ζ上的点(1,0)、(1,-π/2)以及(1,θ)相对应,具体映射关系如图3所示。

映射函数为

研究表明[20-21],映射函数通常取3项既可以保证一定的精度要求又可以使推导过程相对简洁,因此取

式中,R、c1、c3为实常数,且R>0,│c1│+│c3│≤ 1。
在像平面ζ上,令ζ=ρeiφ=ρ(cosφ+isinφ),ρ=1,式(1)与式(2)联立,可得:

选取物理平面z上矩形采场3个特殊点(a,0)、(0,b)和(a,b)分别与像平面ζ上相对应的点(1,0)、(1,-π/2)和(1,φ)分别联立,代入到式(3)中,由前2组对应点易解得:c1=(a−b)/(2R),c3=(a+b)/(2R)−1,联立第3组对应点,可得方程:

解出φ值后,R值即可求出。
2.2 复势函数解析
对式(2)进行如下变换,得出以下相应的解析量:

式中,σ=ζ=eiφ为复变量ζ在巷道边界处的值;为矩形孔口内边界上在x和y方向上的面力分量,由支护体提供;为矩形孔口内边界上所有面力在x和y方向上的主矢量;B、B′、C′可由远场应力σv和σh表示出来[17]:

分析式(8),f0由2部分组成,前一部分为无远场应力,只在孔壁上作用支护阻力的情况,后一部分为只在远场应力作用下,而不施加支护阻力的情况。为了计算简便,可分别求解2种情况围岩应力的复变解析量,如图4所示:

需要规定2个复势函数:
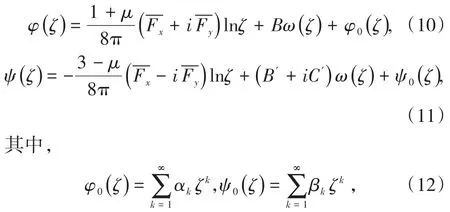
在中心单位圆之内是ζ的解析函数,并且在圆内和圆周上是连续的,可由式(13)并结合柯西积分公式[4],将等号两边ζ的同次项的系数分离后对比求出。

(1)不考虑支护阻力的围岩应力解析量计算(存在远场应力)。无支护作用下的矩形采场受到远场应力σv和σh,孔边界所受面力为0,则,推导出应力解析量为

(2)只考虑支护阻力的围岩应力解析量计算(不存在远场应力)。只有支护作用下的矩形采场只受到孔边界x和y方向上的支护阻力f,而不存在远场应力σv和σh,则,推导出应力解析量为

2.3 矩形采场周边围岩应力分量
将2种不同情况下的应力解析分量式(14)、式(15)进行叠加,即可求出支护作用下矩形采场围岩周边应力解析量:φ(ζ)=φ1(ζ)+φ2(ζ)、ψ(ζ)=ψ1(ζ)+ψ2(ζ),代入式(16)中即可求出同时考虑采场支护和远场应力的矩形采场围岩周边应力分量:

式中,Re指计算时取复数的实部。
3 数值模拟
为了验证复变函数理论求解水平矩形采场围岩周边应力的精确度,基于有限差分法(FLAC3D)开展数值模拟研究,分析采场周边不同位置的应力以及不同支护力下的顶板和侧帮应力演化规律。
3.1 不同位置的应力量
矩形采场位于模型正中央,采场宽×高为20 m×4 m,即宽高比为5∶1,模型上下施加10 MPa的垂向应力,左右施加12 MPa的水平应力,开挖内壁分别施加3~8 MPa的支护力。由于采场四周围岩应力变化具有对称性,因此选取矩形右上角1/4个区域进行分析,即孔口右帮中点到顶板中点90°范围。采场周围不同位置处的垂直应力和水平应力分量解析解和模拟解见表1、表2和图5、图6所示。
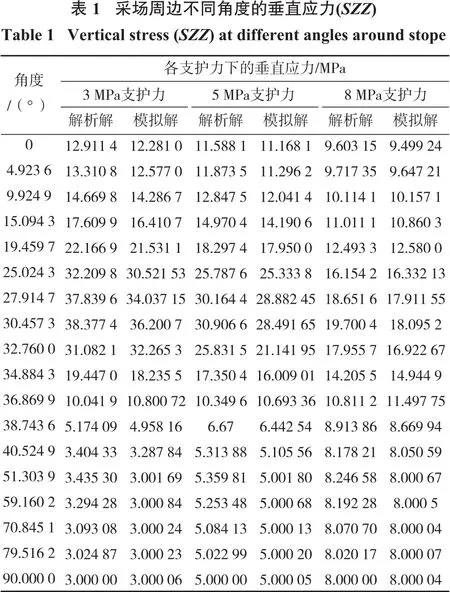



如图5与图6曲线所示,从采场帮壁到顶板,随着角度的增加,围岩垂直应力和水平应力均呈现先增大后减小的趋势,垂直应力峰值出现在约30°位置处,水平应力峰值出现在约35°位置处,即在拐角附近应力值均出现陡增现象,即应力集中区,此结论与李明等[22]的结论保持一致。通过对比解析解和模拟解曲线可知,数值模拟解与理论解析解之间具有比较高的拟合性,理论计算结果具有较好的推广应用价值。
3.2 不同支护围岩周边应力演化规律
对不同支护力条件下采场帮壁和顶板中点应力演化规律分析,即角度分别为0°和90°位置处的围岩径向应力和切向应力。由于采场围岩内壁均匀施加支护阻力f,致使帮壁和顶板中点位置的围岩径向应力等于支护阻力f,因此仅需对帮壁和顶板中点处的切向应力进行分析:在帮壁中点位置处,切向应力为垂直应力SZZ,在顶板中点位置处,切向应力为水平应力SXX。绘制出不同支护力下的帮壁和顶板中点位置的围岩应力演化如图7所示,采场右帮切向应力随支护阻力的增加而减小,而顶板切向应力随支护阻力的增加而增大,且顶板和右帮位置的解析解均略大于模拟解。此外,顶板位置的解析解和数值模拟结果偏差大于右帮位置,对于解析方法来说,原因在于保角变换的映射函数仅取了三项,对于大宽高比采场较长边的应力求解误差增大,实际可通过增加映射函数的项数来提高拟合性[8-9];对于数值模拟方法来说,由于计算机本身的限制,模拟网格的划分对精度产生一定的影响,大宽高比情况下,长边的网格应更加密集。

4 结 论
基于弹性力学的孔口问题,通过复变函数保角变换等理论,将矩形采场转化为单位圆,求解支护作用下围岩周边的应力解析解,并采用数值模拟对理论解析方法结果进行验证,得到以下结论:
(1)复变函数理论和数值模拟方法求解的不同支护力作用下的围岩周边应力解析解和数值解具有比较高的拟合性,理论计算可进行推广应用。
(2)采场周边围岩应力从帮壁到顶板分布先增大后减小,呈现“抛物线”趋势,拐角附近处应力值出现陡增现象,即应力集中现象。
(3)随着矩形采场周围岩体支护阻力的逐渐增加,帮壁切向应力逐渐减小,顶板切向应力逐渐增大,且两个位置的解析解均略大于模拟解。
(4)顶板位置的解析解和数值模拟结果偏差大于两帮位置,对于解析方法来说,原因在于保角变换的映射函数仅取了三项,对大宽高比采场较长边的应力求解误差增大,实际可通过增加映射函数的项数来提高拟合性;对于数值模拟方法来说,由于计算机本身的限制,模拟网格的划分对精度产生一定的影响,大宽高比情况下,可加密长边的网格。
