开口模型下内腐蚀缺陷管柱剩余抗内压强度

刘贤玉， 范村莹， 陈江华， 韩 成， 周玉霞

(1.中海石油(中国)有限公司湛江分公司， 湛江 524057； 2.广东海洋大学海洋工程学院， 湛江 524088)

油气井管柱及输油管道由于内部流体的腐蚀作用，在管柱内壁容易出现局部减薄缺陷，从而降低管柱的承压能力。目前已有文献对含腐蚀缺陷抗内压强度进行实验及数值分析[1-5]。分析含缺陷管柱强度时，一般取包含缺陷的一段管柱进行模拟研究。输油管道由于管道较长，且多处固定，因此在分析含局部缺陷输油管道抗内压强度时，一般在远离缺陷处的模型端面施加轴向约束，即端部约束模型[6-8]；而油气井管柱多为闭口，可自由移动，因此对含缺陷油气井管柱分析时，一般用两端闭口模型进行分析[9-13]。

近年来，海上油田大量采用分层管柱进行开发，鉴于一趟多层管柱后期修井时管柱较难安全起出，一般先用钻杆送入下部分层管柱并悬挂于井筒内，然后再下入上部管柱并插入至下部分层管柱顶部封隔器内。由于上部管柱可小范围的自由活动，且下端开口，在内压载荷下，管柱可视为端部自由开口模型。

目前对缺陷管柱剩余抗内压强度的研究，较少按开口模型进行分析；主要针对某种尺寸管柱分析缺陷深度、长度对强度的影响，较少考虑缺陷宽度、管柱径厚比等其他因素对强度的影响；较少定量分析各因素对抗压强度的影响程度。现基于材料的塑性失效准则，利用非线性有限元方法对开口模型下含内部缺陷管柱的抗内压强度进行研究，并结合正交试验设计，定量分析缺陷参数、管柱尺寸对局部缺陷管柱剩余强度的影响规律，建立抗内压强度多因素预测模型，为油气井工程含缺陷管柱强度的评价提供参考。

1 内缺陷管柱非线性有限元分析

1.1 有限元分析模型结构

主要针对工程上常见的局部内缺陷套管进行研究，分析时对缺陷进行一定的简化，将局部缺陷形状简化处理为方形均匀壁厚缺陷，即缺陷处的壁厚为定值，同时为减小应力集中效应，在缺陷端部以光滑圆弧面过渡。

根据求解问题的对称性，为减少计算单元，取缺陷管柱模型的1/4建立三维有限元模型。为消除边界效应，取计算套管长度为套管外径的3倍，当缺陷长度超过套管外径时，计算长度为缺陷长度的3倍。计算单元采用三维20节点六面体等参单元。在套管厚度方向划分三层网格。由于缺陷处应力变化梯度较大，对缺陷及附近区域划分较密的网格[14]。划分网格后的计算模型如图1所示。

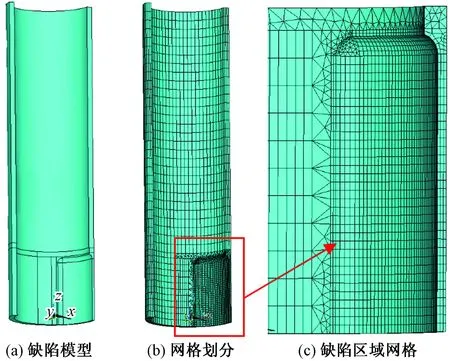
图1 局部均匀减薄缺陷管柱几何模型图Fig.1 Local uniform thinning defect casing geometric model

1.2 边界条件

按管柱两端开口模型进行考虑，只分析内压载荷对管柱强度的影响，忽略其他载荷。由于内压为正对称载荷，在靠近缺陷的管柱端面施加正对称约束，并在纵向剖开面施加正对称约束，由于按开口模型考虑，在远离缺陷的端面不加约束。为避免刚体位移造成的计算不收敛，需选取两个节点约束刚体位移。

1.3 失效准则

失效准则是分析管柱强度的依据，目前对于材料的失效准则有弹性失效准则与塑性失效准则。由于钻井工程中管柱材料一般具有较好的韧性，其破坏形式多为塑性破坏[9]。基于材料塑性失效准则，认为缺陷处Von Mises等效应力全部达到屈服应力后管柱失效。根据第四强度理论，在三维主应力空间，Von Mises等效应力表达式为

(1)

式(1)中：σV为Von Mises等效应力，MPa；σ为许用应力；σ1、σ2、σ3分别为第一、第二、第三主应力。

以海上常用的N80钢级管柱为例进行分析，其最小屈服强度为550 MPa，抗拉强度为650 MPa，弹性模量206 GPa，泊松比0.3。

2 剩余抗内压强度影响因素分析

为研究方便，定义无因次参数，分别为局部缺陷的相对深度(h/T)、缺陷的环向相对宽度(θ/π)、缺陷轴向相对长度(L/D)、管柱径厚比(D/T)、无因次抗内压强度PD，其中：L为缺陷轴向长度，mm；h为缺陷深度，mm；θ为缺陷环形周角， rad；T为管柱壁厚，mm；D为管柱外径，mm；PD=PL/PO，PL、PO分别为缺陷管柱剩余抗内压强度、原始管柱抗内压强度，MPa。

2.1 内压载荷下缺陷管柱应力分布规律

图2为内缺陷管柱在不同内压载荷下等效应力云图，其中缺陷参数：D=177.8 mm，T=10.36 mm，h/T=0.6，θ/π=2/3，L/D=1.5。可以看出，由于缺陷的存在，管柱出现了较明显的应力集中现象，但其影响范围基本限于缺陷区域，在离缺陷较远处，管柱应力分布较均匀，与无缺陷管柱应力分布差别不大。

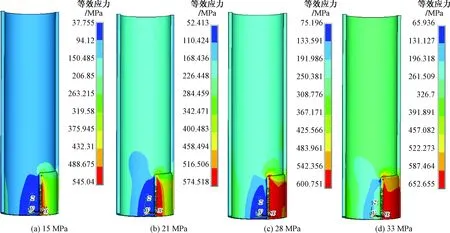
图2 不同内压载荷下缺陷管柱等效应力云图Fig.2 Equivalent stress nephogram of defective pipe string under different internal pressure loads

当载荷较小时，管柱应力、应变与载荷基本呈线性关系，最大应力出现在管柱内部缺陷轴向边缘区域，同时在缺陷中间区域也出现了较大的应力，但其应力值远小于缺陷边缘处应力。当内压增加至15 MPa(原始管柱极限强度的18%)时，缺陷轴向边缘处应力超过了屈服强度550 MPa，最早出现塑性变形。随着载荷继续增加，塑性区域由缺陷边缘逐渐向缺陷中间处、向管柱外表面方向同时扩展，此时虽然载荷增加，但最大应力增加幅度较小。当加载至33 MPa(原始管柱极限强度的39%)时，塑性区扩展至整个缺陷区域，此后应力、应变开始大幅度增加，此时缺陷处最大应力已达到材料的极限拉伸强度。缺陷区全部屈服后，继续加载，缺陷处变形会急剧增加，有限元分析不收敛，因此可认为缺陷区全部屈服后，管柱失去承载能力。

图3为三种模型下缺陷管柱应力随内压载荷的变化曲线，可以看出相同载荷下，不同模型下缺陷处最大应力较为接近，但缺陷处最小应力有明显差异，其中开口模型下应力最大，端部约束模型次之，闭口模型应力最小。在内压载荷下，管柱承受较大的环向应力，而端部约束模型与闭口模型会使管柱内部产生附加轴向拉应力，可降低管柱Von Mises等效应力，对塑性区的扩展有一定的延缓作用，从而提高承压能力。如对于缺陷参数：D=177.8 mm，T=10.36 mm，h/T=0.6，θ/π=2/3，L/D=1.5，开口模型、端部约束模型、闭口模型下抗内压强度分别为33.1、36.5、37.4 MPa。

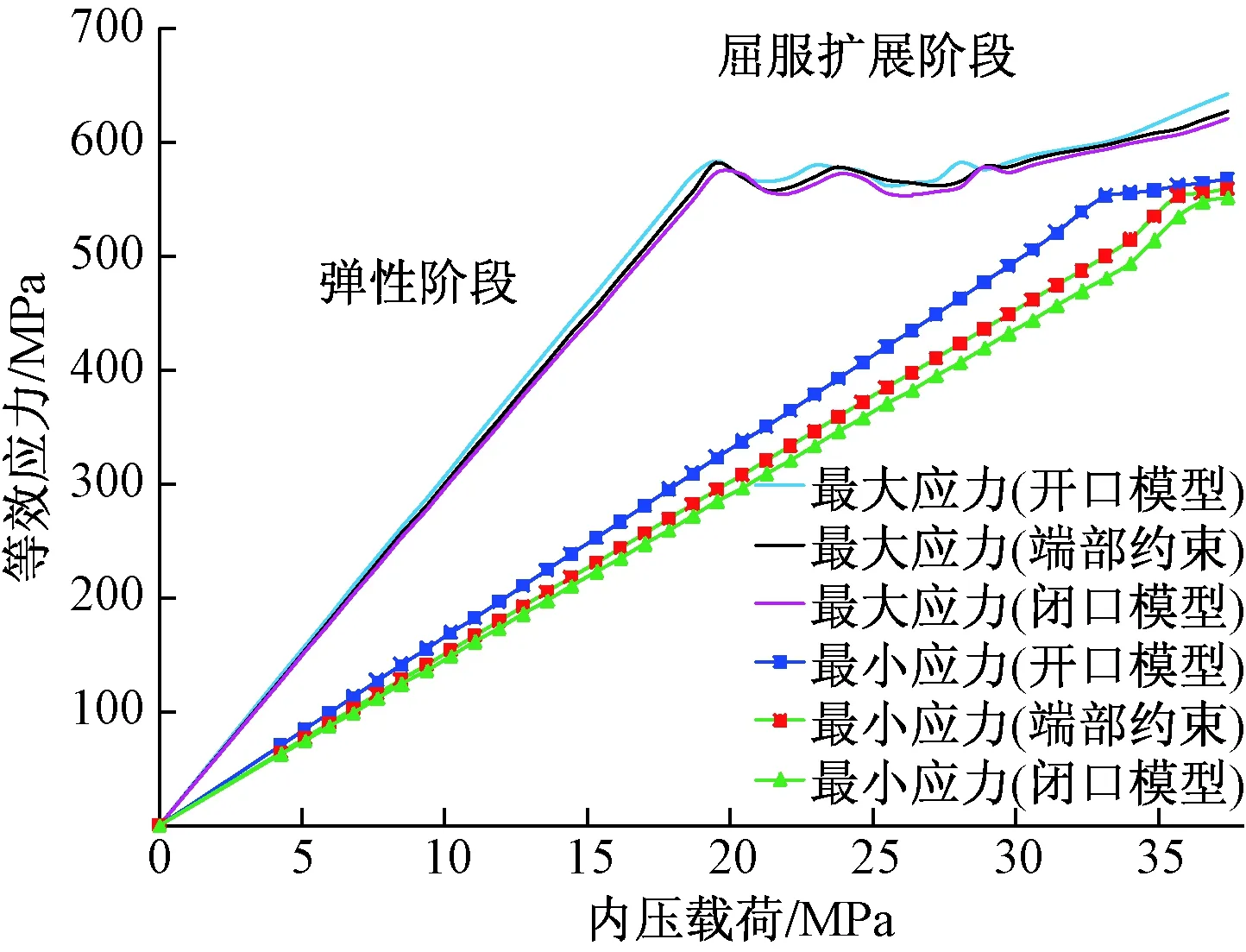
图3 不同模型下等效应力随内压载荷的变化曲线Fig.3 Curves of equivalent stress with internal pressure load under different models

图4 缺陷相对深度对无因次抗内压强度影响(D=177.8 mm，T=10.36 mm)Fig.4 Effect of relative defect depth on dimensionless internal compressive strength(D=177.8 mm，T=10.36 mm)

2.2 缺陷相对深度对强度的影响

缺陷相对深度(h/T)对管柱的抗内压强度的影响较大，其抗内压强度随缺陷相对深度增加大致呈线性关系降低，如图4所示。当缺陷相对深度小于0.3时，缺陷相对深度对抗内压强度的影响幅度相对较小，而当缺陷相对深度超过0.3之后，缺陷相对深度对抗内压强度的影响幅度明显增加。

如对于缺陷参数θ/π=1/4、L/D=0.6，当缺陷相对深度h/T从0.15增加到0.3时，抗内压强度降低9.1%，而缺陷相对深度从0.45增加到0.6时，抗内压强度降低16%。另外当缺陷长度较小时，抗内压强度随深度的增加降低幅度较小；当缺陷长度较大时，抗内压强度降低的幅度较大。

2.3 缺陷相对长度对强度的影响

随着缺陷相对长度的增加，剩余抗内压强度呈指数关系递减，如图5所示。当缺陷相对长度(L/D)<0.6时，缺陷管柱抗内压强度随长度的增加而急剧降低；当相对长度(L/D)>0.6后，抗内压强度随长度的增加而逐渐降低，并趋于极限值。相对长度(L/D)>2时，长度的变化对抗内压强度的影响已基本可以忽略，如缺陷相对长度(L/D)从2增加到5时，其抗内压强度仅下降1%左右，此时抗内压度已基本接近管柱整体减薄时抗内压强度。另外可以看出h/T=0.6时，相对宽度分别为θ/π=1/4、1/2、5/6的三条关系曲线基本重合，表明缺陷宽度对管柱抗内压强度影响较小。

图5 缺陷相对长度对无因次抗内压强度的影响(D=177.8 mm，T=10.36 mm)Fig.5 Effect of relative defect length on dimensionless internal compressive strength(D=177.8 mm，T=10.36 mm)

2.4 缺陷相对宽度对强度的影响

缺陷相对宽度(θ/π)对抗内压强度影响较小，如图6所示。缺陷相对宽度对抗内压强度影响可分为两阶段。

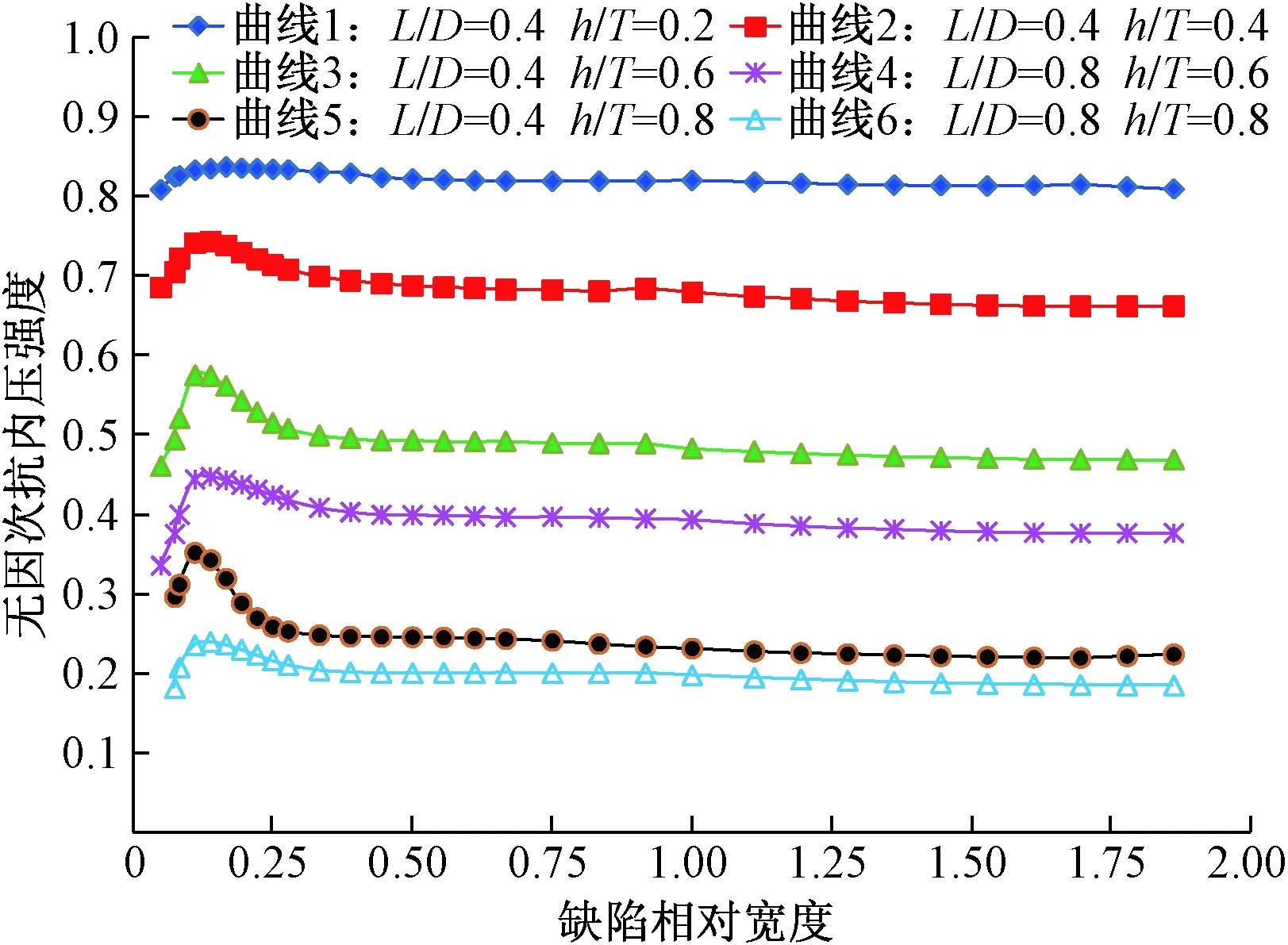
图6 缺陷相对宽度对无因次抗内压强度的影响(D=177.8 mm，T=10.36 mm)Fig.6 Effect of relative defect width on dimensionless internal compressive strength(D=177.8 mm，T=10.36 mm)

第一阶段当缺陷宽度θ小于临界宽度θe时，抗内压强度随宽度增加而增加。此时缺陷接近轴向沟槽。近似沟槽形缺陷导致的应力集中将显著降低管柱的抗内压强度，因此抗内压强度随着长度的减小而急剧降低，特别是当缺陷相对深度较深、缺陷长度较长时，这种影响更为明显。有限元分析表明，临界宽度θe与缺陷深度、缺陷长度关系不大，基本为定值，回归确定临界宽度θe计算式为

θe=0.138π

(2)

式(2)中：θe为缺陷临界宽度，rad。

第二阶段当缺陷宽度θ超过临界宽度θe后，抗内压强度随缺陷宽度增加而减小，但随着宽度的增加，抗内压强度降低的幅度变小，当θ超过0.4π后，抗内压强度变化不大，但下降趋势依然存在，如缺陷宽度从0.4π增加到1.8π时，其抗内压强度最大可下降4%左右，因此出于安全考虑，工程上不应忽略缺陷宽度对抗内压强度的影响。

2.5 管柱径厚比对强度的影响

从图7可以看出，管柱径厚比对抗内压强度有较大影响，径厚比较小时，径厚比的变化对无因次抗内压强度影响幅度较大，但随着径厚比的增加，径厚比变化对无因次抗内压强度的影响逐渐减弱，当管柱径厚比超过25时，径厚比对无因次强度的影响较小，如径厚比从25增加到40时，无因次抗内压强度变化幅度最大为2%。

管柱径厚比(D/T)对无因次抗内压强度影响规律因缺陷长度、深度不同而差异较大。当缺陷长度与缺陷深度比值较大时，无因次抗内压强度随径厚比(D/T)增加而增大。而当缺陷长度与缺陷深度比值较小时，无因次抗内压强度随径厚比(D/T)增加而降低。

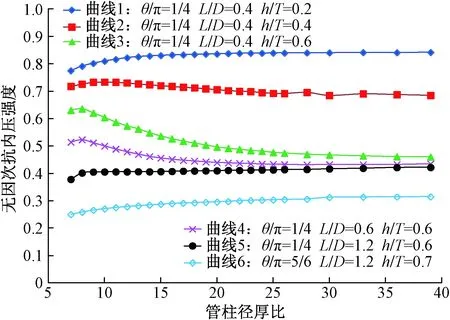
图7 管柱径厚比对无因次抗内压强度影响(D=177.8 mm)Fig.7 Effect of diameter-thickness ratio on dimensionless internal compressive strength(D=177.8 mm)

2.6 管柱外径对强度的影响

从图8可以看出，当缺陷的相对深度(h/T)、相对宽度(θ/π)、相对长度(L/D)、管柱的径厚比(D/T)一定时，管柱外径对无因次抗内压强度基本无影响。因此如果两种管柱缺陷在几何尺寸上相似，便可认为其无因次抗内压强度相同。

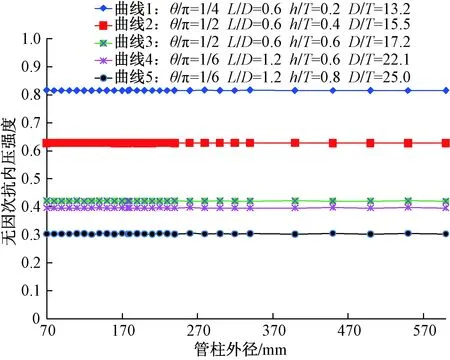
图8 管柱外径对无因次抗内压强度影响Fig.8 Influence of pipe outer diameter on dimensionless internal compressive strength

3 无因次抗内压强度主控因素分析

为定量分析多因素对抗内压强度的影响规律，采用正交试验设计方法，对缺陷相对长度、相对宽度、相对深度、管柱径厚比、管柱外径五个影响因子各取4种不同水平，具体如表1所示。通过正交试验L16(45)设计了16个计算模型，对每个模型采用有限元方法分析无因次抗内压强度，通过极差分析确定各因素对抗内压强度的影响程度。

正交试验结果如表2所示，从极差结果可以看出，影响无因次抗内压强度的因素依次为缺陷深度、缺陷长度、管柱径厚比、缺陷宽度。深度是影响无因次抗内压强度最显著的因素，深度对无因次抗内压强度的影响程度，约为缺陷长度影响程度的2倍，为径厚比影响程度的6倍，为缺陷宽度的12倍，而管柱外径的影响基本可以忽略。

表2中R1、R2、R3表示各因素不同水平下均值的变化幅度。缺陷深度对应的R1、R2、R3分别为0.111、0.185、0.180，其R1较小，而R2、R3相近，表明随着缺陷深度的增加，无因次抗内压强度的变化幅度先增加后趋于平稳，即缺陷深度较小时，缺陷深度对抗内压强度影响相对较小，而缺陷较深时，抗内压强度与缺陷深度呈线性关系；缺陷长度对应的R1、R2、R3分别为0.176、0.050、-0.008，其绝对值快速递减并趋于零，表明随着缺陷长度的增加，无因次抗内压强度变化幅度在急剧变小，缺陷较长时，可以忽略长度的变化对强度的影响；管柱径厚比对应的R1、R2、R3分别为-0.052、-0.022、0.017，其绝对值呈逐渐递减趋势，即随着径厚比增加，径厚比对抗内压强度的影响幅度逐渐变小，当径厚比较大时，径厚比的变化对强度的影响较小，但不可忽略；缺陷宽度对应的R1、R2、R3分别为-0.034、0.006、0.019，R1绝对值明显大于R2、R3绝对值，表明缺陷宽度较小时，宽度对抗内压强度较大，当缺陷宽度较大时，宽度对抗内压强度影响较小，但不可忽略。

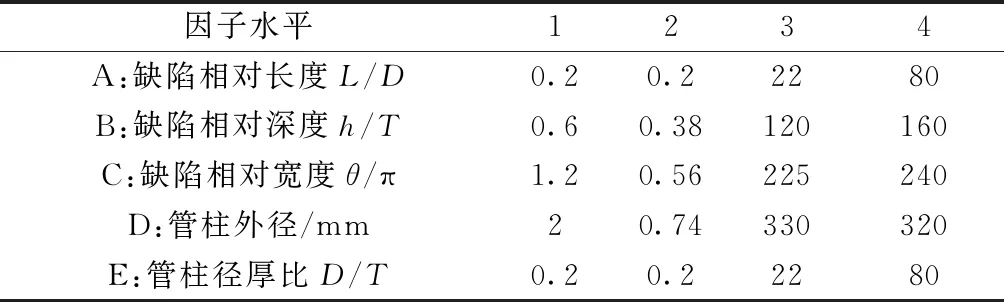
表1 无因次内压强度影响因素及水平取值

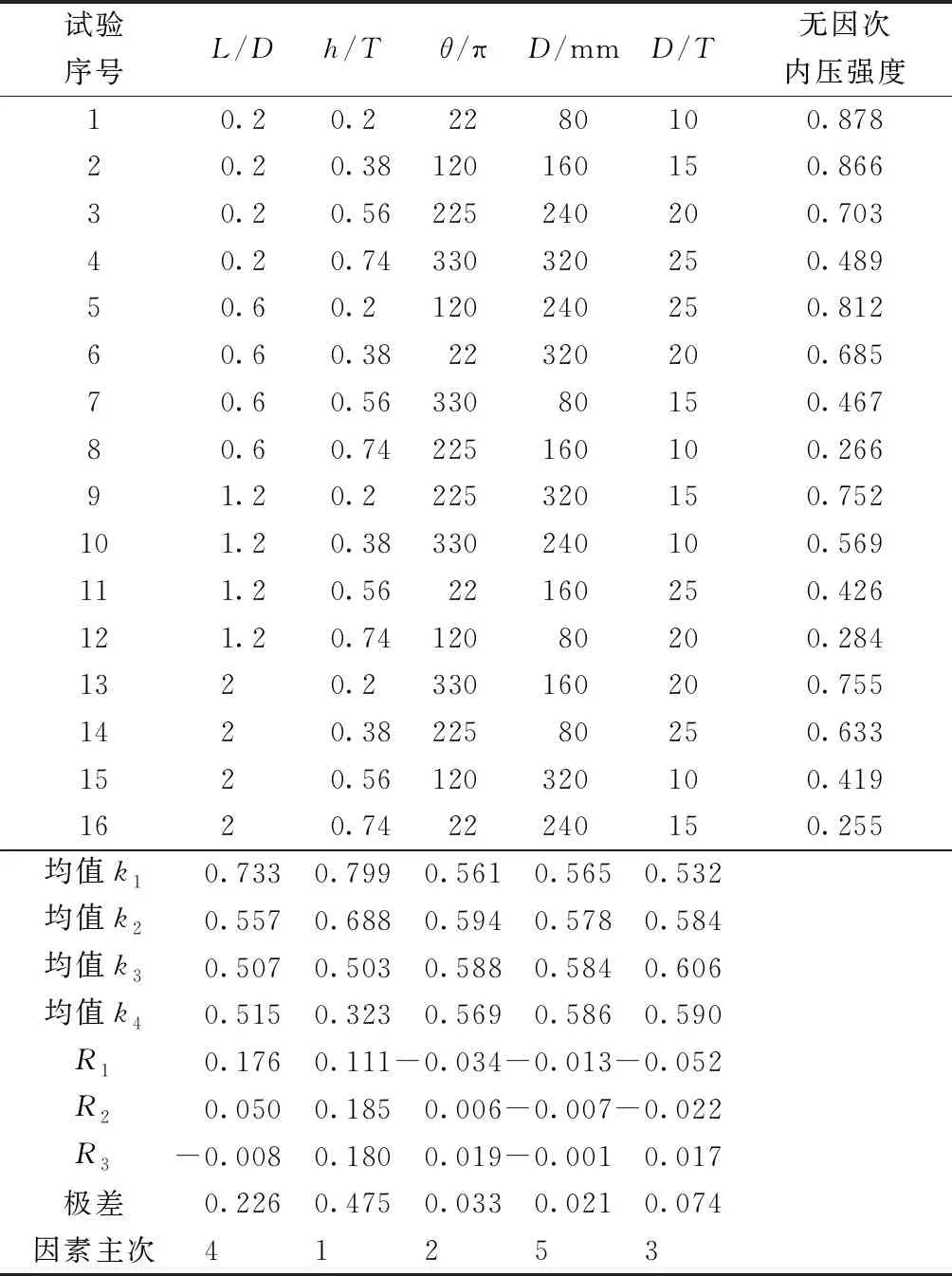
表2 无因次内压强度影响因素正交试验结果

4 剩余抗内压强度工程计算

利用有限元方法分析了692例不同情况下含缺陷管柱的抗内压强度，根据缺陷长度、宽度、深度、管柱外径、径厚比等对抗内压强度的影响，对计算结果进行拟合，得到局部均匀内缺陷管柱无因次抗内压强度多因素预测模型为

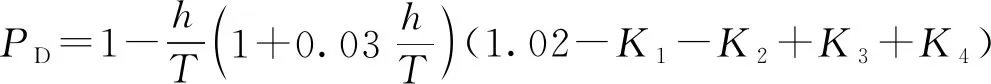
(3)

式(3)中：K1为缺陷宽度影响因子；K2为缺陷长度影响因子；K3为管柱径厚比影响因子；K4为缺陷长度深度综合影响因子，其计算式分别为

(4)

(5)

(6)

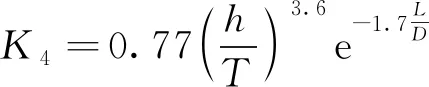
(7)

拟合公式相关系数为0.984，图9为预测结果与有限元计算结果的相对误差，误差为正则表明公式预测结值小于有限元软件计算结果，平均绝对误差1.38%，除26个预测点相对误差较大之外，其余误差均较小，在4%以内，大部分预测点误差在2%以内，拟合结果较为理想。

误差较大的预测点中，有14个点管柱径厚比小于10或径厚比大于32的情况，另外12个点相对深度与相对长度比值(hD/TL)超过3.5。本预测模型主要针局部较大面积的腐蚀缺陷管柱抗内压强度计算，当相对深度与相对长度比超过3.5时，缺陷接近为孔径小而深的点蚀坑，此时本预测模型将产生较大的误差。考虑到钻采工程所用油套管的径厚比一般处于10～30，因此预测公式可基本满足钻井工程需要。用无因次抗内压强度PD乘以原始管柱的抗内压强度PO，即可得到含缺陷管柱剩余抗内压强度PL。该井实际注水期间，注入压力正常，后期修井更换管柱时，未现管柱穿孔及明显变形。

图9 公式预测值与有限元计算结果的相对误差Fig.9 Relative error between formula prediction results and finite element calculation results

5 应用实例

南海西部涠洲某油田分层注水井，井深3 243 m，下入φ244.5 mm生产套管固井后进行射孔完井。下部分层管柱悬挂封隔器斜深3 091 m，垂深1 985 m。上部注水管柱插入至分层管柱封隔器内，上部管柱外径φ88.9 mm，钢级为N80。该井CO2分压0.52 MPa，由于采取先期排液，油管为非防腐材质，可能存在腐蚀。采用机械测井技术检测上部注水管柱腐蚀情况，测得管柱内腐蚀缺陷尺寸参数如表3所示，需要评价管柱抗内压强度能否满足注水期间抗内压强度要求。

依据式(3)评价该井生产管柱腐蚀后的抗内压强度，结果如表3所示，管柱最小无因次抗内压强度PD=0.68，剩余抗内压强度为74.8 MPa。注水期间最大注入压力15 MPa，注水管柱最大内压35 MPa，即带腐蚀缺陷管柱可满足注水期间的抗内压强度要求，另外校核管柱可满足抗拉、抗外挤强度要求。

6 结论

(1)开口模型下含缺陷管柱抗内压强度低于端部约束模型与闭口模型。内缺陷管柱抗内压强度随缺陷深度增加呈线线关系降低，随缺陷长度的增加呈指数关系降低，并趋于极限值；抗内压强度随缺陷宽度增加先增加后减小，并趋于极限值；管柱径厚比对无因次抗内压强度影响规律因缺陷长度、深度不同而差异较大。

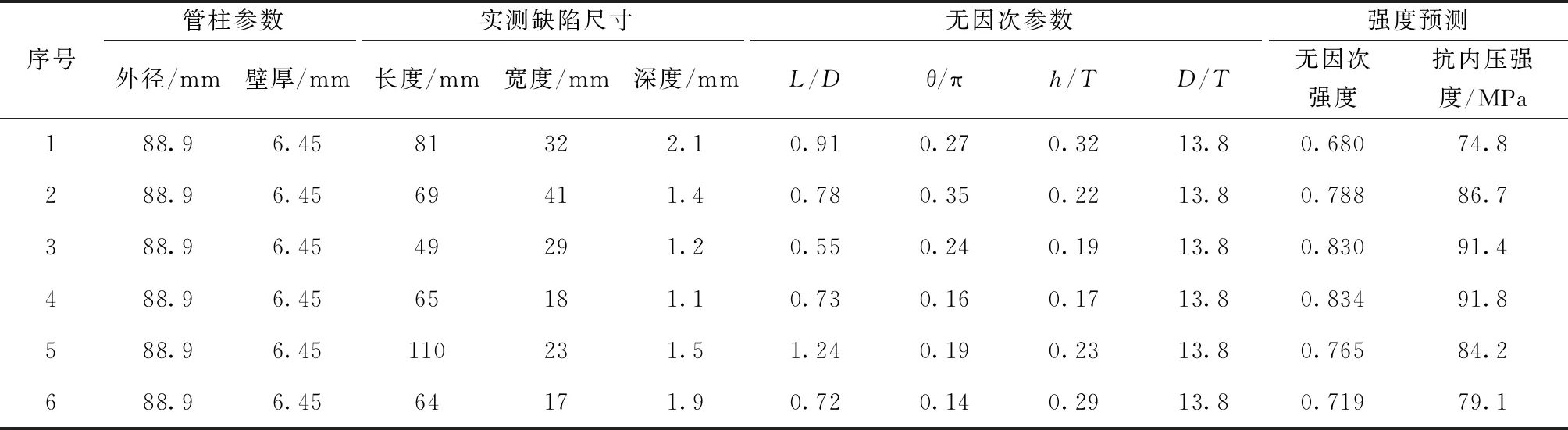
表3 某注水井实测油管内腐蚀缺陷尺寸及强度预测结果

(2)深度是影响内缺陷管柱无因次抗内压强度最显著的因素，深度对无因次抗内压强度的影响程度，约为缺陷长度影响程度的2倍，为径厚比影响程度的6倍，为缺陷宽度的12倍，管柱外径对无因次抗内压强度的影响可以忽略。

(3)基于非线性有限元分析结果，建立了抗内压强度多因素预测模型，模型预测值与有限元分析结果误差较小，可为工程含缺陷管柱抗内压强度的评价提供参考。