开孔建筑内压风洞试验及其与国内外规范对比

陈 胜，黄 鹏，顾 明

（同济大学土木工程防灾国家重点实验室，上海200092）

在台风等风灾破坏中，当风致碎片冲击并损坏建筑的围护结构以后，原本处于封闭状态的建筑将会产生开孔，从而导致建筑内部风压突然增大，对开孔建筑的安全性造成巨大的威胁［1-2］。因此，在开孔建筑的抗风设计中，建筑内部风压的取值是保证建筑抗风安全性重要的一部分。开孔建筑的风致内压响应是一个复杂的问题，有很多因素都会导致开孔建筑内压发生变化，例如建筑周边地貌环境、开孔的位置和大小、建筑背景孔隙率和结构的柔度等［3-5］。但是在实际建筑抗风设计中，建筑物的外形、背景孔隙率以及柔度等特性区别较大，很难将所有因素对开孔建筑内压的影响都考虑在内。特别是对于风荷载规范，由于其需要广泛的适用性，故应在对开孔建筑内压系数取值时考虑最主要的影响因素。

目前世界上各个国家的风荷载规范对开孔建筑风致内压取值的规定有较大的不同。日本建筑学会在本国规范［6］中指出，开孔建筑内压的计算必须考虑开孔在墙面上的大小，但其只定义了封闭建筑的内压系数，取值为0或-0.4。我国在《建筑结构荷载规范》［7］中不仅定义了封闭建筑的内压系数，还根据开孔率的大小定义了开孔建筑的内压系数。美国土木工程师协会提出的ASCE7-16规范［8］将建筑分成封闭式和开敞式等不同类型，并根据建筑类型给出了相应的内压系数。澳大利亚/新西兰AS/NZS 1170.2：2011规范［9］对开孔建筑内压系数的定义最为详细，不仅给出了建筑迎风面开孔时的内压系数，还定义了开孔位于侧风面、背风面和屋面时的内压系数。需要说明的是，各国风荷载规范中定义的内压系数均为开孔建筑内部风压的平均值。

本文首先通过风洞试验对开孔低矮房屋模型的内压响应进行了测量，讨论了开孔孔口周边的外部风压、风向角、风场湍流强度和开孔率对开孔建筑内压均值响应的影响，并从时程和功率谱两方面分析了开孔结构内部风压与开孔孔口周边外压的相关性。然后将风洞试验结果与当前国内外具有代表性的3种风荷载规范：我国《建筑结构荷载规范》、美国规范ASCE7-16规范以及澳大利亚/新西兰规范AS/NZS 1170.2：2011进行了对比。最后对这3种规范在开孔建筑内压系数取值方面的准确性进行评价，并分析了它们各自的优势和不足之处。

1 风洞试验概况

1.1 试验模型及测点布置

开孔建筑内压响应试验在同济大学土木工程学院土木工程防灾国家重点实验室的TJ-2大气边界层风洞完成，TJ-2大气边界层风洞是一个闭口回流式矩形截面风洞。在开孔结构的内压研究中，美国德州理工大学风工程研究现场试验室的TTU（Texas Tech University）建筑模型具有较广泛的应用［10］，许多研究人员均以此建筑为原型进行开孔结构的风致内压研究［11-12］，因此本文也采用TTU模型作为建筑原型进行刚性风洞试验研究。试验模型长548 mm，宽364 mm，高160 mm，缩尺比为1：25，如图1。该模型采用双层有机玻璃板制作而成，将测压管线布置在双层板中间，减小了在来流作用下测压管对结构内压的干扰。双层板板厚为10 mm，因此模型内部长528 mm，宽344 mm，高150 mm，内部容积为0.027 m3。主开孔布置在模型的迎风面上，可通过拆卸并更换不同的迎风面来模拟不同面积大小的开孔。风洞试验风向角以来流垂直于开孔墙面为0°，逆时针方向为正风向角，如图2所示。根据对称性，试验风向角范围取为0°到180°，间隔为10°。

图1 TTU刚性测压试验模型Fig.1 TTU rigid test building model

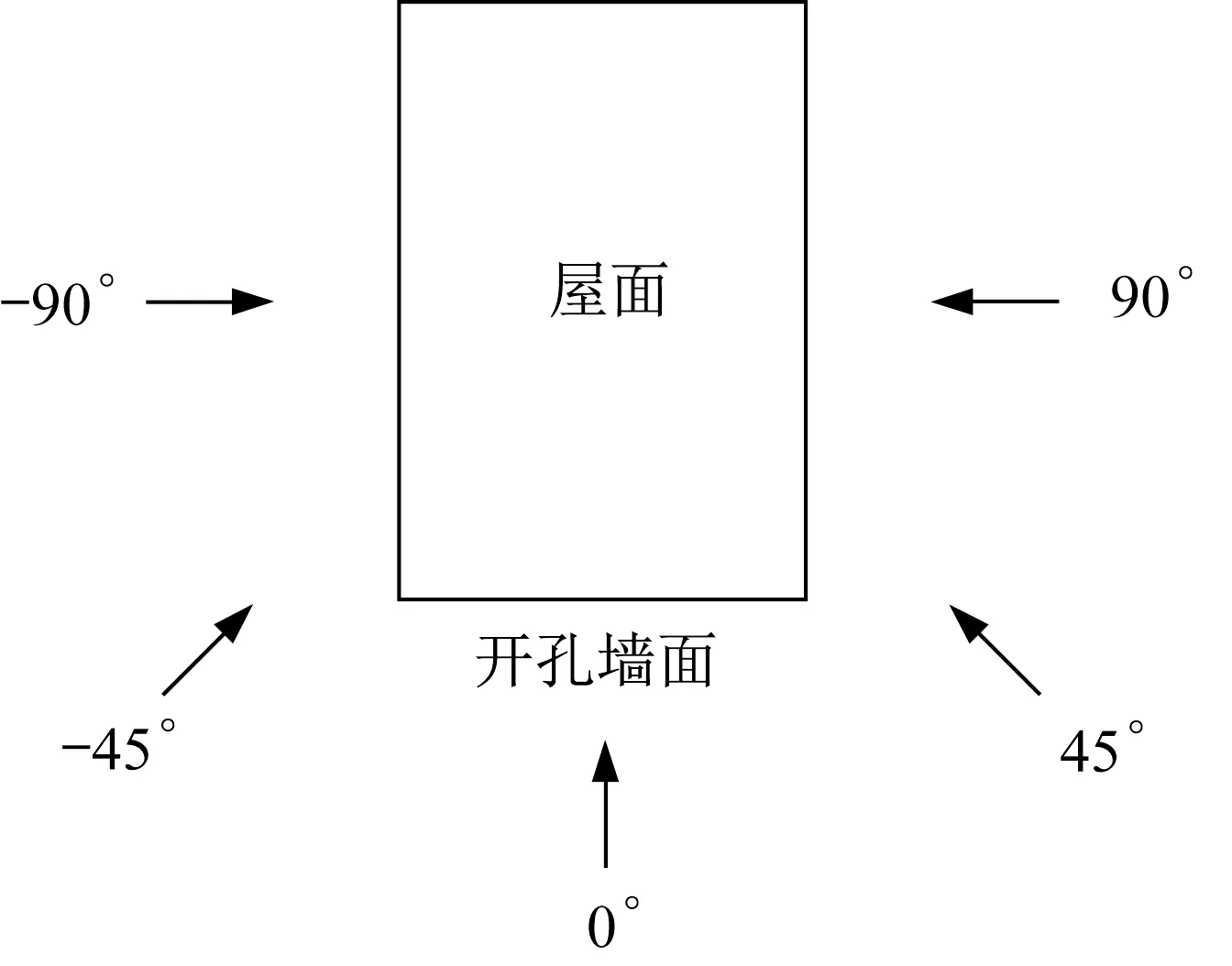
图2 风向角定义Fig.2 Definition of wind direction

在屋面布置了20个内压测点，左右墙面各布置了15个内压测点，背风面布置了12个内压测点，迎风面根据开孔大小的不同布置了22或20个内压测点。其中位于开孔孔口周边的8个测点为内外压双面测点，目的是为了分析孔口周边的外部风压与开孔结构内压的相关性，内外风压满足同步测量的要求，测点布置图如图3所示。为了研究开孔面积（开孔率）对内压响应的影响，设置了4种位于迎风面正中心、面积不同的方形开孔，其边长分别为31、53、68和81 mm，对应的开孔率（开孔面积与开孔墙面面积之比）分别为0.017、0.048、0.079和0.112。

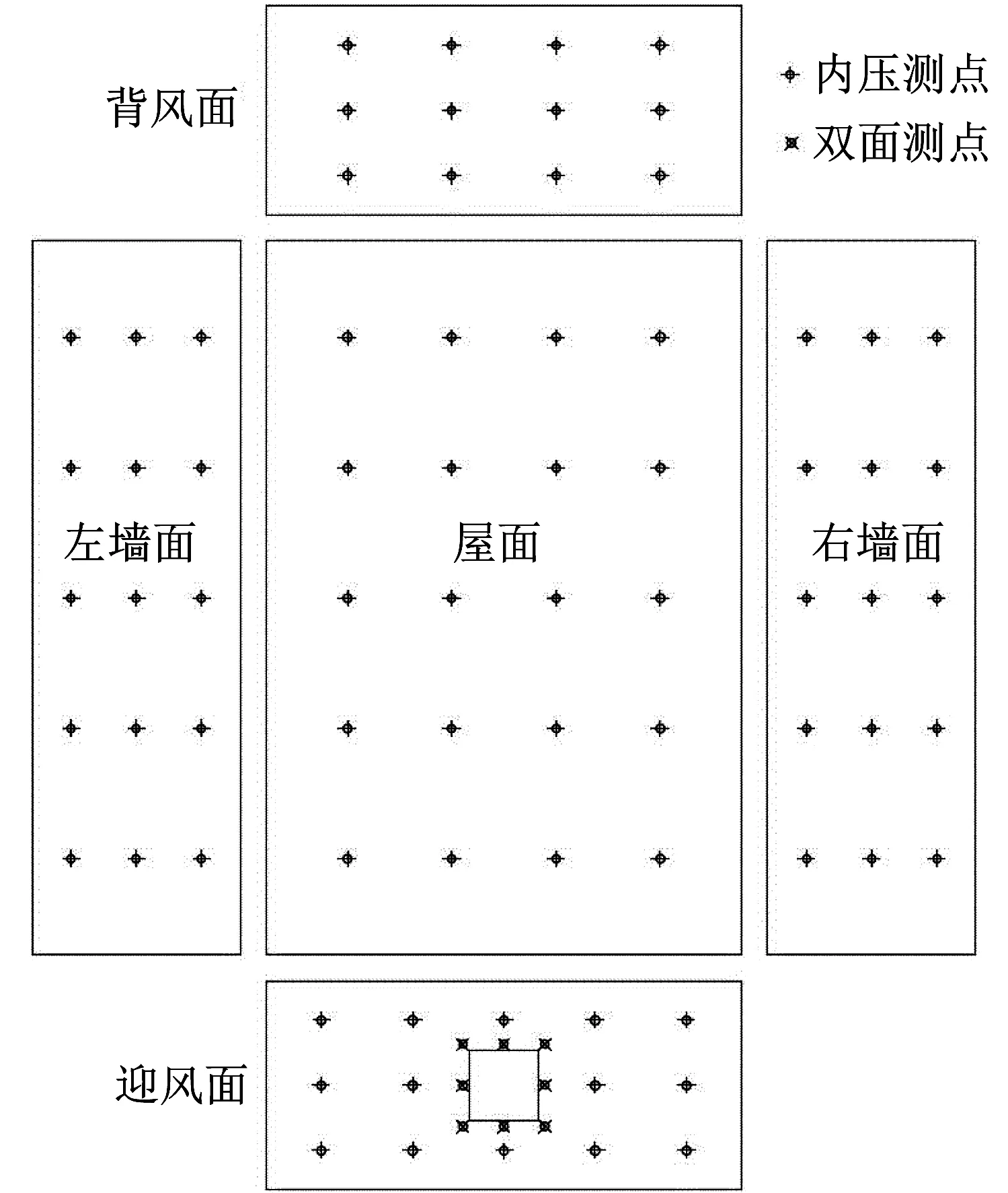
图3 测点布置Fig.3 Layout of pressure taps

1.2 风场模拟

试验采用被动模拟的方法实现所需风场的模拟，为了研究湍流强度对开孔结构内压响应的影响，需保证模型开孔处范围内的湍流强度一致，因此模拟的风场需为均匀湍流场。此外，为了消除地面边界层对均匀湍流场的影响，试验设置了一个高20 cm、直径100 cm的圆形试验平台（如图1所示），将模型从地面抬高20 cm，从而确保模型开孔处范围内的湍流场是均匀的。图4为从圆形试验平台表面开始算起风洞试验中模拟的3种均匀风场的平均风速剖面、湍流度剖面和开孔中心高度处的风速功率谱，模型迎风面开孔处的风速均保持为10 m·s-1。图中，参数n为频率，Su（n）为风速功率谱函数，σ2为风速方差，Lu为湍流积分尺度，U为风速均值。从图中可知，在模型最大开孔高度范围4～12 cm内，平均风速和湍流度均相差不大，在此范围内风场1、2、3的湍流强度分别约为0.014、0.094和0.176，均满足均匀风场的要求，且试验风速功率谱与Karman谱吻合良好。

图4 各风场平均风速剖面、湍流度剖面及风速功率谱Fig.4 Profiles of mean wind speed and turbulence intensity,and wind speed spectra for three wind fields

风压测量采用Scanivalve电子压力扫描阀系统，采样频率为312.5 Hz，采样时间设置为28.8 s，即每个测点的采样数据为9 000个。由于试验风速和实际风速比为1：1，模型缩尺比为1：25，根据相似定律，28.8 s采样时间对应的实际采样时间为12 min，大于10 min，满足规范要求［7］。

2 风洞试验结果分析

2.1 内压与孔口周边外压的相关性

2.1.1 内外压随风向角变化

图5为开孔周边外部风压系数和开孔模型内部风压系数随风向角的变化曲线，开孔孔口尺寸为53 mm×53 mm（开孔率0.048）。需要说明的是，在对内压数据进行处理前，首先对内压在结构内部不同位置处的空间分布特性进行了分析，结果表明不论在正风向还是斜风向下，开孔结构的平均和脉动内压均具有较好的空间相关性，即在开孔结构内部均匀分布。因此，数据处理中将采用所有内压测点数据的平均值代表开孔结构内压响应的大小，而孔口周边外压系数也均为所有外压测点测得数据的平均值。由图可见，不论在哪个风向角下，该开孔尺寸的内压响应大小与孔口周边的外部风压都非常接近，外压只比内压稍大一些。当风向角大于60°以后，内外压系数均开始由正值（压力）变成负值（吸力）。因此，开孔结构平均内压系数的大小需要根据开孔孔口周边外压系数的大小来确定，后文的规范对比将对此进行相关的讨论。

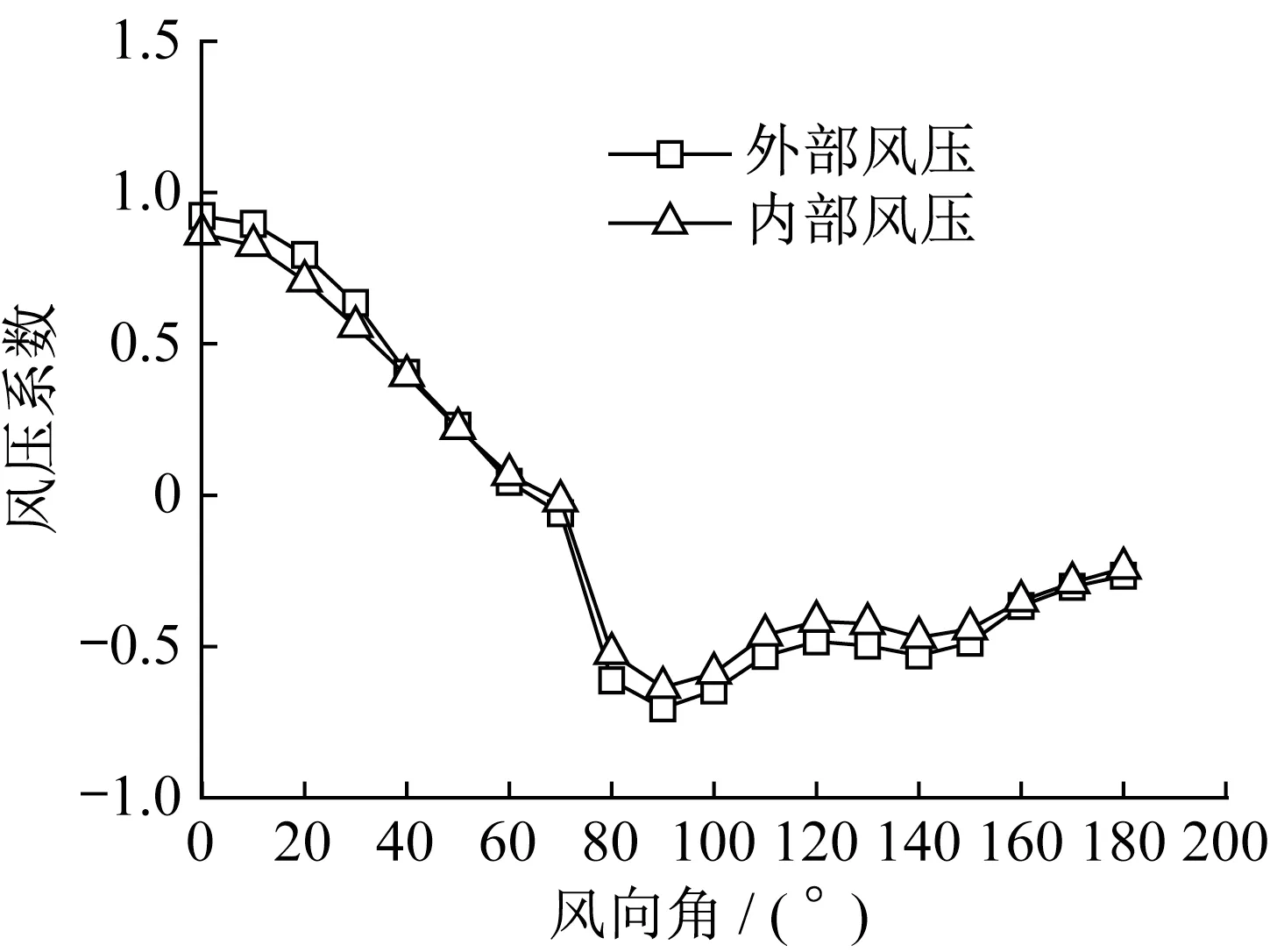
图5 平均外压和内压系数随风向角变化Fig.5 Mean external and internal pressure coefficients as a function of wind direction

2.1.2 内外压响应时程相关性

图6对比了开孔尺寸为53 mm×53 mm的模型，在0°正风向角和70°斜风向角下的内压系数与孔口周边外压系数的时程变化曲线。由图可见，无论在0°还是70°风向角下，开孔结构的内压响应与孔口周边外压响应在时程上均具有高度的同步性，且不会受到风向角的影响。

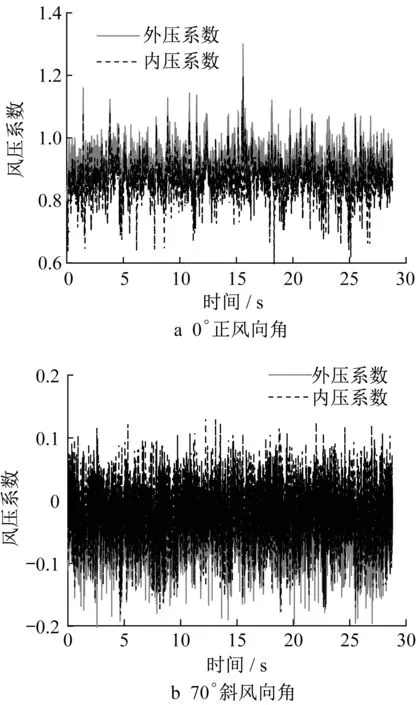
图6 孔口周边外压系数与内压系数时程曲线对比Fig.6 Comparison of time histories of external pressure coefficient around orifice and internal pressure coefficient

2.1.3 内外压响应功率谱相关性

为了进一步分析开孔结构内压动力响应的特性及其与孔口周边外压响应之间的关系，图7对比了在0°正风向角和70°斜风向角下，开孔尺寸为53 mm×53 mm时模型内外压系数的功率谱曲线。从图中可以看出，虽然内外压响应功率谱的同步性没有内外压响应时程的同步性那么高，但是在0°正风向角下仍然表现出了一定的相关性，并且彼此之间相差不大。而在70°斜风向角下，内外压系数功率谱函数则有很大的区别，尤其是在内压功率谱函数曲线上，出现了2个共振峰，内压系数功率谱在这2个共振峰的频率附近明显大于外压系数功率谱。根据相关研究的结论，这2个共振峰可能是由于斜风剪切流在孔口处产生的漩涡脱落与内压Helmholtz共振导致的［13-15］。

为了更直观地对比内外风压系数功率谱函数的大小，将内压系数功率谱与外压系数功率谱的比值定义为内压导纳，并将0°正风向角和70°斜风向角的开孔模型内压导纳曲线绘于图8中。由图可见，在0°正风向角下，总体上内外压系数功率谱相差不大，内压导纳的值基本在1左右的范围内波动。但是在70°斜风向角下，内压导纳波动很大并且也出现了2个明显的峰值，其最大值甚至超过了10，这意味着内压系数功率谱可能比外压系数功率谱大10倍以上。因此，开孔结构的内压响应在功率谱上与孔口周边外压在斜风向角下存在很大的差异。

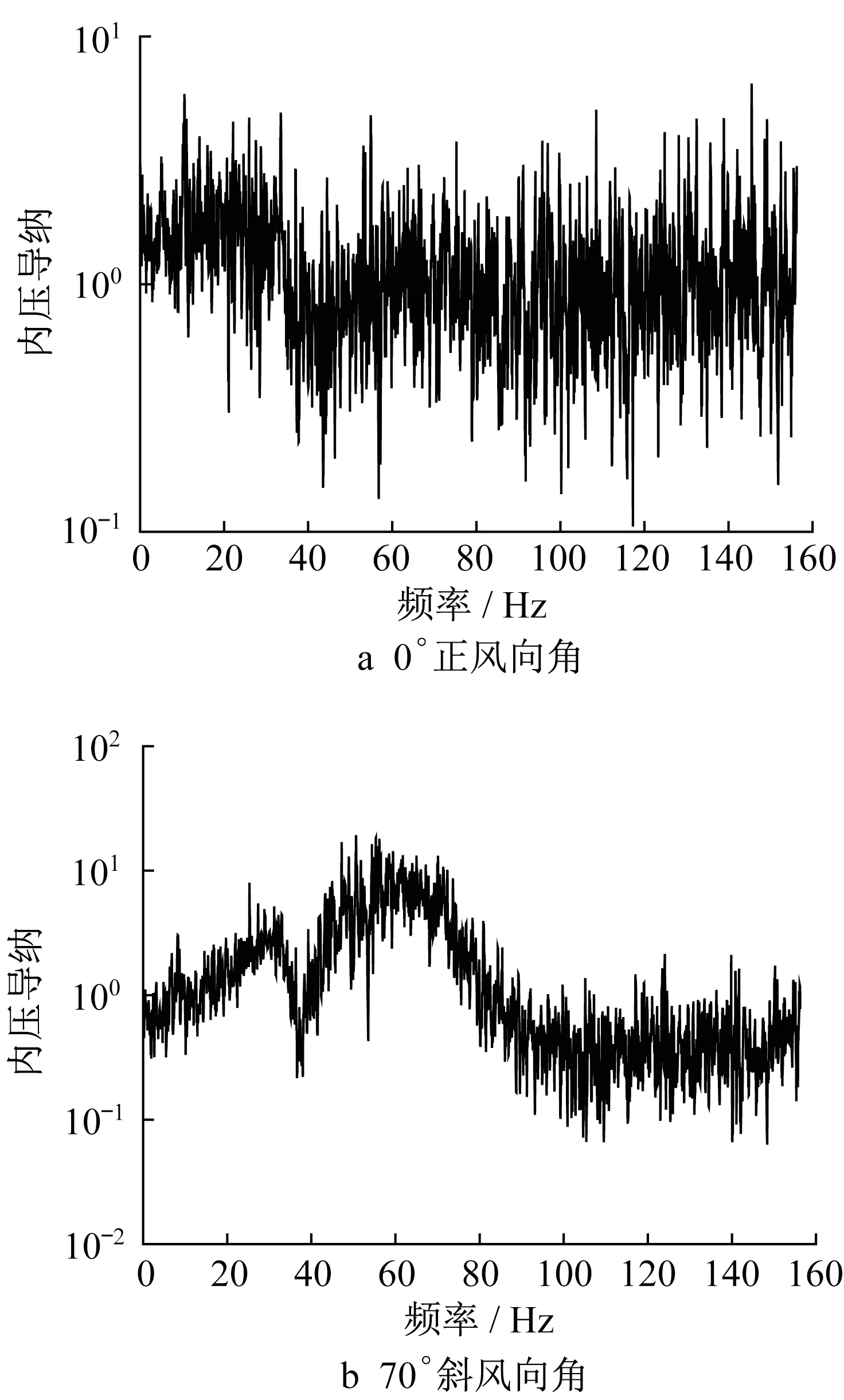
图8 内压系数导纳曲线Fig.8 Admittance curves of internal pressure coefficient

2.2 湍流强度的影响

建筑物周边不同类型的地貌会导致来流湍流强度发生很大的变化，对开孔建筑的内压响应具有不可忽略的影响。图9为来流风速为10 m·s-1时，边长53 mm的方形中心开孔结构在3种不同湍流度的均匀湍流风场中平均内压系数随风向角的变化曲线。由图可见，在同一风向角下，湍流度越大，开孔结构的平均内压系数越大，这意味着较大的湍流度将会增强开孔结构的内压均值响应。此外不论来流湍流度多大，平均内压系数的最大正值均出现在0°风向角时，即开孔墙面垂直于来流方向。但是平均内压系数的最大负值出现在90°风向角下，即开孔墙面平行于来流方向，而不是大于90°的风向角，即迎风墙面位于背风面时。

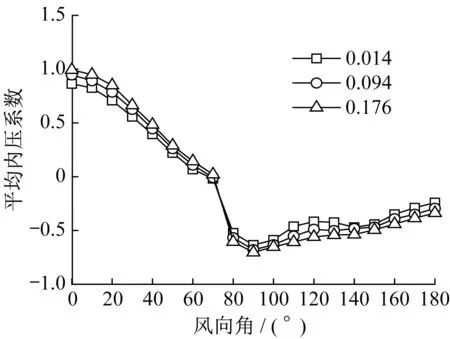
图9 3种湍流风场中平均内压系数随风向角变化Fig.9 Mean internal pressure coefficients as a function of wind direction for three turbulent wind fields

2.3 开孔面积（开孔率）的影响

图10为边长分别为31、53、68和81 mm（开孔率分别为0.017、0.048、0.079和0.112）的4种方形中心开孔结构在10 m·s-1来流风速下平均内压系数随风向角的变化曲线。由图可见，在同一风向角下，开孔结构的平均内压系数随开孔面积的增大而增大，这是因为较大的开孔面积增大了外部风压对内部风压的影响，同时还减小了内压体系的阻尼比［16］，导致开孔结构的内压响应更加强烈。此外，随着开孔面积的增大，内压均值响应的增大幅度却逐渐减小，当开孔面积为68 mm×68 mm（开孔率0.079）和81 mm×81 mm（开孔率0.112）时，它们的平均内压系数在各风向角下几乎都相等。因此，当开孔率达到0.1左右后，开孔建筑的平均内压系数随开孔面积的进一步增大变化很小。

图10 不同开孔面积的平均内压系数随风向角变化Fig.10 Mean internal pressure coefficients with different opening sizes as a function of wind direction

3 风洞试验结果与各国规范的对比

3.1 对比我国规范GB 50009—2012

我国《建筑结构荷载规范：GB 50009—2012》规定，建筑物内部压力的局部体型系数可按下列规定采用：①封闭式建筑物。按其外表面风压的正负情况取-0.2或0.2。②仅一面墙有主导孔口的建筑物。当0.02＜δ≤0.10时，取0.4μsl；当0.10＜δ≤0.30时，取0.6μsl；当δ＞0.30时，取0.8μsl。③其他情况。按开放式建筑物的μsl取值。其中，δ为开孔率；系数μsl为外部风压局部体型系数，即外部平均风压系数，此处应取主导孔口对应位置的值，对应风洞试验模型的开孔迎风墙面局部体型系数μsl取值应为1.0。由此可计算，当开孔墙面正对风向时不同开孔率对应的开孔建筑内压系数，并将其与风洞试验结果进行对比，如图11所示。

图11 规范和风洞试验的内压系数随开孔率变化对比Fig.11 Comparison of mean internal pressure coefficients as a function of opening ratio in Chinese code and wind tunnel test

从图中可以看到，无论开孔多大，风洞试验结果均远大于规范取值。需要特别说明的是，这里风洞试验的结果是在湍流度为0.014的均匀风场中得到的，而在规范中的体型系数值是基于B类风场（田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇地区）10 m高度处的基本风速定义的，其对应的风场湍流度为0.14。根据前文开孔结构平均内压系数随来流湍流度的变化规律可知，湍流度越大，平均内压系数也越大，所以如果增大风洞试验中的湍流度使其与规范一致，将进一步增大试验的内压均值响应结果，从而使规范的取值与风洞试验结果相差更大。因此，我国现行风荷载规范较大低估了开孔结构风致内压的取值，需要较大幅度提高目前所规定的内压体型系数。

3.2 对比美国规范ASCE7-16

美国规范ASCE7-16将建筑物分为4类：全封闭式、部分封闭式、开敞式和部分开敞式。①全封闭式建筑：外部风压为正压的墙面上的开孔总面积A0不超过0.37 m2或该墙面总面积Ag的1%中的较小值。②部分封闭式建筑：外部风压为正压的墙面上的开孔总面积A0应大于建筑其他围护结构（墙面和屋面）上的开孔总面积A0i的1.1倍，并且外部风压为正压的墙面上的开孔总面积A0大于0.37 m2或该墙面总面积Ag的1%中的较小值，且建筑其他围护结构（墙面和屋面）的开孔率不超过20%。③开敞式建筑：建筑每个墙面上的开孔率都不小于80%。④部分开敞式建筑：不符合全封闭式、部分封闭式或开敞式建筑物要求的建筑物。规范ASCE7-16给出了以上各类建筑的内部风压系数的取值，如表1所示。

表1 ASCE7-16内压系数取值Tab.1 Internal pressure coefficient of ASCE7-16

本文风洞试验模型开孔尺寸对应的开孔率分 别 为0.017、0.048、0.079和0.112，均 满 足0.01Ag＜A0＜0.8Ag，并且试验中所有模型的开孔均为建筑围护结构上的单个开孔，即A0i=0，故风洞试验的开孔模型均属于部分封闭式建筑类型。将风洞试验的结果与规范ASCE7-16的取值进行对比，如图12所示。由图可见，规范ASCE7-16对开孔建筑内压系数的取值远小于风洞试验获得的内压系数，并且随着开孔率的增大二者的差距也越来越大，规范ASCE7-16低估了开孔建筑的内压系数。由风洞试验结果可知，开孔建筑的平均内压系数随开孔面积的增大而增大，而规范ASCE7-16并没有区分开孔率在0.01～0.80范围内（部分封闭式建筑）的开孔建筑内压系数，因此现行规范ASCE7-16对开孔建筑内压系数的取值方法较粗略，应该基于开孔率的大小对其进行更细致的区分。

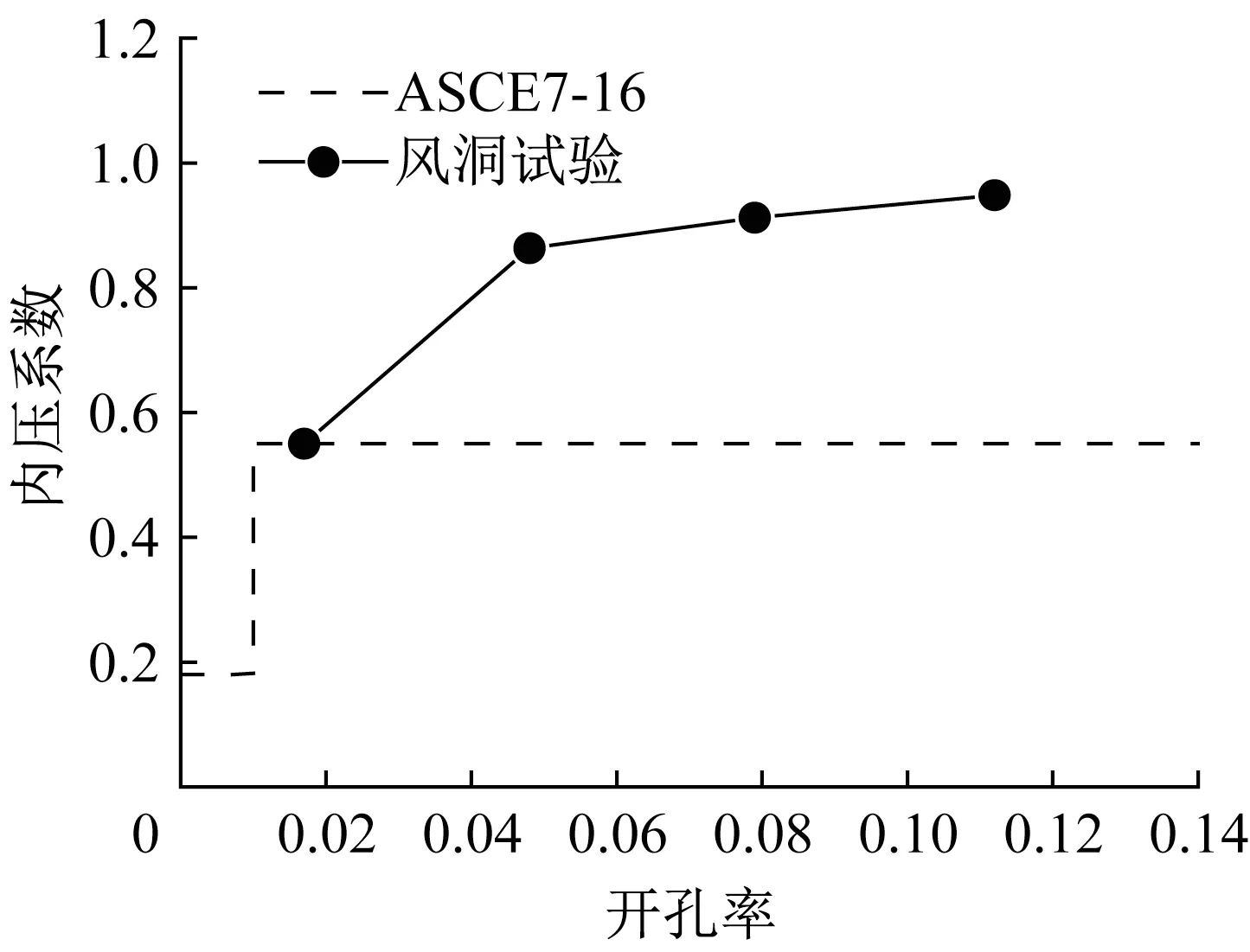
图12 ASCE7-16和风洞试验内压系数随开孔率变化对比Fig.12 Comparison of mean internal pressure coefficients as a function of opening ratio in ASCE7-16 and wind tunnel test

3.3 对比澳大利亚/新西兰规范AS/NZS 1170.2：2011

在当前各国的风荷载规范中，澳大利亚/新西兰规范AS/NZS 1170.2：2011对开孔建筑内压系数的取值定义最为详细，其不仅给出了开孔位于迎风面时的内压系数，还给出了开孔位于侧风面、背风面和屋面时的内压系数。具体取值方法如表2所示。表中，Cpe为最大开孔所在位置处对应的外压系数，ε为某个表面上的开孔面积与其他表面上开孔面积的比值。

本文进行风洞试验的模型均为单开孔结构，因此主开孔墙面上的开孔面积与建筑其他表面上的开孔面积之比不小于6，则由表2可知，不论开孔位于迎风面、背风面还是侧风面上，建筑的内压系数均等于外压系数Cpe。根据规范AS/NZS 1170.2：2011的相关规定，可得与风洞试验建筑模型相对应的外压系数，从而确定其开孔状态下的内压系数，分别为：开孔位于迎风墙面上时为0.8，开孔位于背风墙面时为-0.3，开孔位于侧风墙面时为-0.5。将规范AS/NZS 1170.2：2011对内压系数的取值与风洞试验结果进行对比，如图13所示。

表2 AS/NZS规范内压系数取值Tab.2 Internal pressure coefficient of AS/NZS code

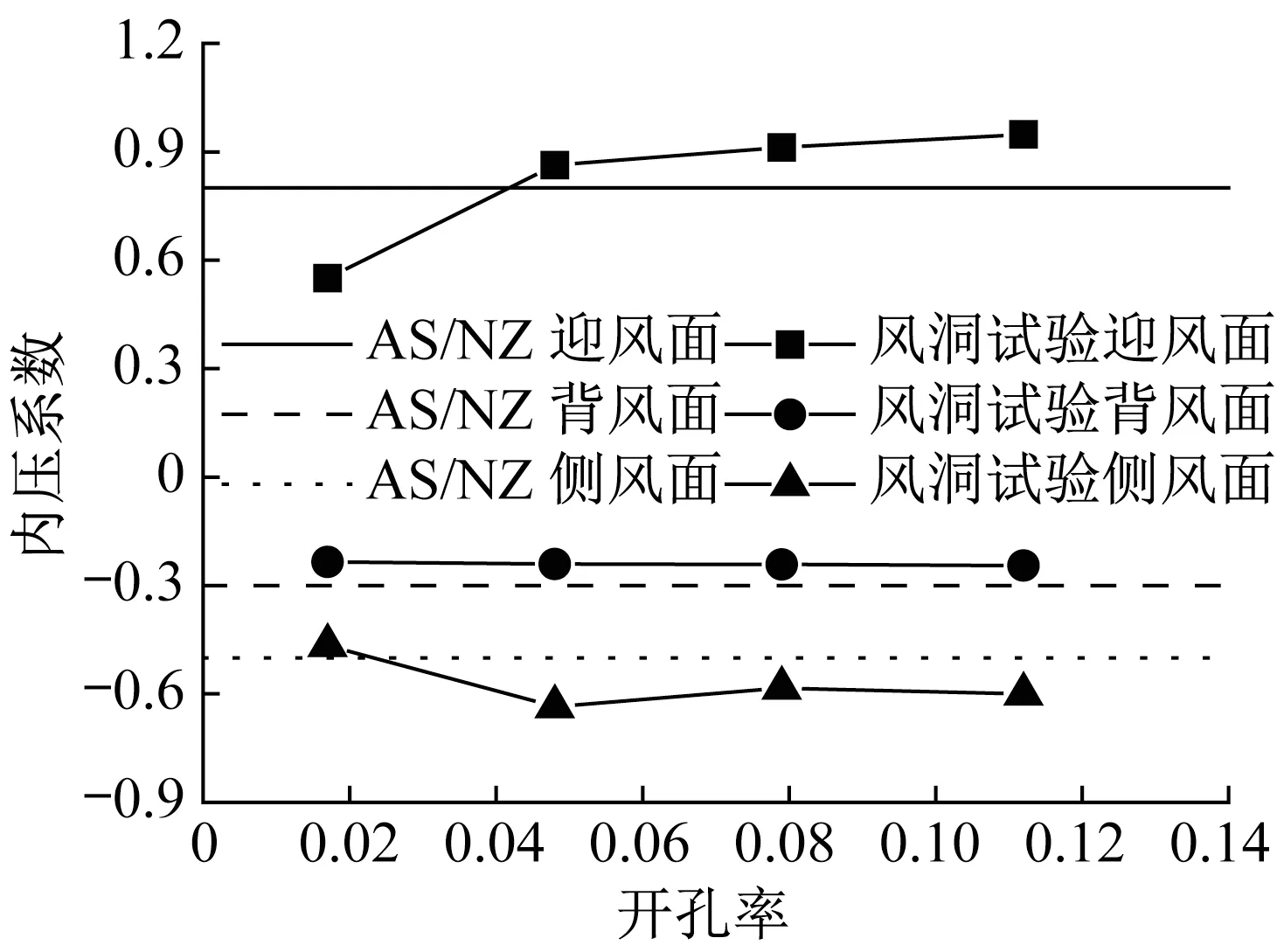
图13 AS/NZS规范和风洞试验内压系数随开孔率变化对比Fig.13 Comparison of mean internal pressure coefficients as a function of opening ratio in AS/NZS code and wind tunnel test

由图中可以看到，总体上规范AS/NZS 1170.2：2011的取值与风洞试验的吻合程度较为理想。开孔面积的大小对内压系数的影响在开孔位于迎风墙面上时最明显，对开孔位于侧风墙面时的影响相对较小，而当开孔位于背风墙面上时，开孔建筑的内压大小几乎不会受到开孔面积的影响。因此，为了改进现行方法的不足，AS/NZS风荷载规范可以考虑在开孔位于迎风和侧风墙面时，根据开孔率的大小对开孔建筑的内压系数进行更细致的区分。

3.4 3种风荷载规范的比较

通过对比以上3种风荷载规范对开孔建筑内压系数的取值方法可以发现，各国规范考虑影响内压系数的因素包括开孔率的大小、开孔处的外部风压以及开孔所在墙面的风向角。由风洞试验结果可知，这些因素对开孔结构的风致内压响应均有显著的影响。但是这3种规范在区分内压系数时对这些因素考虑的侧重点却有所不同，并不是每个因素都考虑在内，具体可总结成如表3所示。

表3 3种规范定义内压系数时考虑的因素Tab.3 Factors considered in three codes determining internal pressure coefficient

从表中可以看到，我国《建筑结构荷载规范》考虑了开孔率和外部风压对开孔结构内压系数的影响，但是不足是只给出了主导孔口位于迎风墙面时的内压系数，缺乏当开孔位于侧风墙面和背风墙面等其他墙面上时对内压系数的定义。美国规范ASCE7-16只简单考虑了开孔率的大小对内压系数的影响，但并没有区分开孔率在0.01～0.80范围内（部分封闭式建筑）的内压系数，并且通过风洞试验结果可知，开孔建筑的内压大小与孔口周边的外压密切相关，而规范ASCE7-16对内压系数取值时并未考虑开孔处的外压大小。澳大利亚/新西兰规范AS/NZS 1170.2：2011的最大特点是不仅定义了开孔位于迎风墙面的内压系数，还定义了开孔位于侧风墙面、背风墙面和屋面时的内压系数，并且考虑了外部风压与内部风压的联系，但是它并未根据开孔率的大小对内压系数进行更细致的区分。

另一方面，通过对比这3种规范的内压系数取值与风洞试验的结果还可以发现澳大利亚/新西兰规范AS/NZS 1170.2：2011的内压系数取值与风洞试验结果比较吻合，但是我国《建筑结构荷载规范》和美国规范ASCE7-16都较大低估了开孔建筑内压系数的大小。因此在对各国规范的改进中，我国和美国的规范都应该增大内压系数的取值，并且可以考虑加入对开孔位于侧风墙面、背风墙面和屋面等建筑其他表面时内压系数的定义，而澳大利亚/新西兰的规范应该基于开孔率的大小对开孔建筑的内压系数进行更细致的区分。

4 结论

设计了3种均匀湍流风场进行开孔低矮建筑的内压风洞试验，讨论了孔口周边外部风压、风向角、风场湍流强度和开孔面积（开孔率）对开孔建筑平均内压系数的影响，同时将风洞试验结果与国内外现行风荷载规范进行了对比，分析了当前各国风荷载规范中对开孔建筑内压系数取值的准确性以及各自的优势和不足，得到了一些适用于当建筑的门窗等围护结构在风灾中遭受破坏从而产生主开孔时，其内部平均风压系数大小变化情况的结论。主要研究结论如下：

（1）开孔结构的内压大小与开孔孔口周边的外压大小密切相关。在正风向角和斜风向角下，开孔结构的内压响应与孔口周边外压在时程上均具有高度的同步性，但是斜风向角时的内压响应与孔口周边外压在功率谱上存在很大的差异。由于内压共振响应的存在，斜风向角时内压系数功率谱在共振频率附近明显大于外压系数功率谱，且相差可能高达10倍以上。

（2）当孔口位于迎风墙面正中心，且来流方向垂直于开孔墙面时（0°风向角），开孔建筑的平均内压系数最大，但是当来流方向平行于开孔墙面时（90°风向角）平均内压系数负值最大。对于湍流度的影响，在同一风向角下，来流湍流度越大，开孔建筑的平均内压系数也越大。

（3）在同一风向角下，较大的开孔面积（开孔率）将增大开孔建筑的内压均值响应，但是开孔建筑内压均值响应的增大幅度随开孔面积的增大而减小，当开孔率达到0.1左右后，开孔建筑的平均内压系数随开孔面积的进一步增大在任一风向角下变化都很小。

（4）我国《建筑结构荷载规范》较大低估了开孔建筑内压系数的大小，当前规范应提高不同开孔率区间的内压体型系数取值，此外还应该考虑增加对开孔位于侧风墙面、背风墙面和屋面等其他风向角下内压系数取值的规定。

（5）美国规范ASCE7-16对开孔建筑内压系数的取值普遍小于风洞试验的结果，且没有区分开孔率在0.01～0.80范围内（部分封闭式建筑）内压系数的差别，与实际情况相差较大。

（6）澳大利亚/新西兰规范AS/NZS 1170.2：2011对内压系数的取值与风洞试验结果吻合较好，并且较准确地定义了开孔位于侧风和背风墙面时的内压系数。但是当开孔位于迎风和侧风墙面时，可以考虑根据开孔率的大小对开孔建筑的内压系数进行更细致的区分。

作者贡献说明：

陈胜：提出研究思路，设计研究方案，负责风洞试验，采集和分析试验数据，撰写论文。

黄鹏：修改研究方案，获取研究经费，指导风洞试验实施和论文撰写，审阅和修改论文。

顾明：参与论文选题和设计，修改研究方案，审阅和修订最终版本论文。