依托传统数学文化 实施学科育人

王伟

摘要：在博大精深的中华优秀传统文化中，蕴含着丰富的数学文化。教师应充分挖掘数学传统文化内容，并将其恰当地应用在数学教学中，以增进学生对数学知识背景的了解和掌握，更好地发挥数学学科的育人导向功能。具体地，可以从以传统数学文化内容弘扬中华传统美德，以传统数学文化内容拓宽解题思路，以传统数学文化内容增长历史文化知识，以传统数学文化内容增强民族自豪感四个方面入手。

关键词：传统文化;数学文化;学科育人

教育部颁布的《完善中华优秀传统文化教育指导纲要》中强调，加强中华优秀传统文化教育，是深化中国特色社会主义教育和中国梦宣传教育的重要组成部分，是构建中华优秀传统文化传承体系、推动文化传承创新的重要途径，是培育和践行社会主义核心价值观、落实立德树人根本任务的重要基础。

在博大精深的中华优秀传统文化中，蕴含着丰富的数学文化。很多古代数学著作中的内容都适合用来融入当前的数学课堂，以增进学生对教学知识背景的了解和掌握。通过增加这些传统数学文化内容，也能更好地发挥数学学科的育人导向功能。

一、以传统数学文化内容弘扬中华传统美德

西汉时期，苏武临大节而不辱，经磨难而不屈，其坚贞不屈的民族气节和强烈的爱国之心历来被人们所传颂。《算法统宗》就记载了“苏武牧羊”一题：“当年苏武去北边，不知去了几多年，分明记得天边月，二百三十五番圆。”235÷12=19余7。学习完两位数除多位数后，就可以让学生尝试计算苏武被扣押在匈奴北海牧羊的时间来使学生体悟苏武的这种骨气。其间，还可以渗透如下数学文化：中国古代采用的是阴阳历，秦朝统一执行的颛顼历为十九年增加七个闰月，也就是说每19年中有12年每年12个月，另外7年每年增加1个闰月，共有13个月。

孝顺长辈、感恩父母是中华传统美德的重要组成部分。《算法统宗》记载：“张家三女孝顺，归家探望勤劳。东村大女隔三朝，五日西村女到。小女南乡路远，依然七日一遭，何曰齐至饮香醪，请问英贤回报。”学生在利用最小公倍数的知识解决这一古代数学问题的同时，还可以培养他们尊敬父母、关爱父母的良好品质。

韩愈的治学名言：“书山有路勤为径，学海无涯苦作舟”是中华民族勤奋好学的生动写照。《算法统宗》记载了“诵课倍增”和“书生分卷”两道古算题：“有个学生心性巧，一部孟子三日了。每日增添整一倍，问君每天读多少”？（《孟子》一书共计34685个字）“毛诗春秋周易书，九十四册共无余。毛诗一册三人读，春秋一本四人呼。周易五人读一本，要分每样几多书。就见学生多少数，请君布算莫踌躇。”学生在学习这些古代数学问题时，古人那种热爱学习、刻苦攻读的良好品德也会深深感染当代的小学生。

勤劳是中华民族的传统美德，我们应引导学生树立正确的劳动价值观，弘扬劳动精神，创造美好生活。学习《张邱建算经》和《九章算术》的“女子善织”;《孙子算经》的“河妇荡杯”;《算法统宗》的“赵嫂织麻”等古算题，可以使学生充分感受到中国古代劳动妇女勤劳善良的优秀品质。

二、以传统数学文化内容拓宽解题思路

《九章算术》中的方田章曾记载这样一道数学题：“今有十八分之十二，问约之得几何？”此题是求[1218]约分等于多少？中国古代数学史并无质数一说，更谈不上分解质因数。我们祖先利用独到的“更相减损术”来求两个数的最大公因数：“可半者半之;不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。”其意为（12，18）→（6，9）→（6，3）→（3，3）。最后，用[69]的分子和分母同时除以9和6的最大公因数3得到[23]。显而易见，如果越大的两个数求最大公因数，更相减损术相对分解质因数来说，优势更加明显。我国古代数学素来以计算见长，由此可见一斑。

《九章算术》则记载了“凫雁相逢”一题：“今有凫（凫即野鸭）起南海，七日至北海;雁起北海，九日至南海。今凫雁俱起，问何日相逢？”学生可以按工程问题的解法，1÷（[17]+[19]）=3[1516]日。古人的齐同术（并日数为法，日数相乘为实，实如法而一）又为我们提供新的解题思路：野鸭7天可行1个单程，63天可行9个单程;大雁9天可行1个单程，63天可行7个单程。63天野鸭与大雁一共可行16个单程，因此共同行1个单程需要63÷（9+7）=3[1516]日。

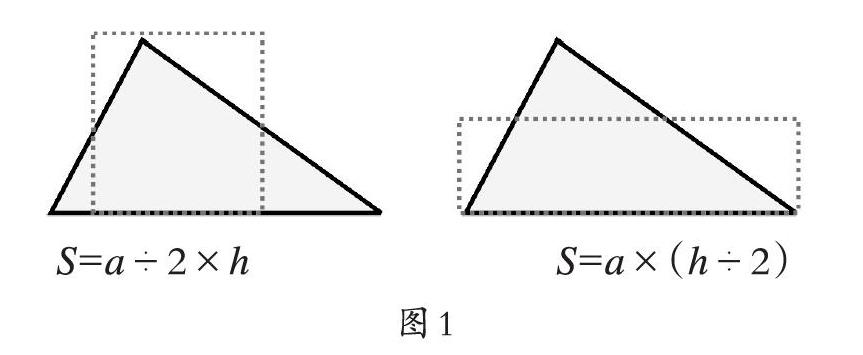
《九章算术》中“方田章”二十五题记载：“今有圭田广十二步正从二十一步，问为田几何？”（三角形田底12步，高21步。问这块地的面积是多少。）“术曰：半广以乘正从。”（底的一半乘高）借助图1可以让学生深刻理解古人这一计算方法蕴含的道理。同时，也可以让学生进一步思考：底乘高的一半也可以求三角形的面积，怎样借助图形加以说明呢？借助古人的智慧，拓宽了学生的解题思路，转化的数学思想也得以更好地培养。

S=a÷2×h S=a×（h÷2）

“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这道耳熟能详的“鸡兔同笼”问题记载在《孙子算经》中，在我国民间流传甚广，流傳到日本后，还被变化为“龟鹤算”。当前，我们很多版本的小学数学教材都收录了此题。学生可以通过画图、列表、假设等方法解决这个问题。《孙子算经》给出这样一种解决此问题的独到方法：“上置头，下置足，半其足，以头除足，以足除头，即得。”意思是：上面放头数，下面放脚数，脚数除以2，再用头数减半脚数就是兔子的数量，再用兔子的数量减头数，就是鸡的数量。结合此题为：

第一行35353523鸡

第二行94471212兔

程大位在《算法统宗》中还给出另外的两个解法：一是“倍头减足折半是兔”，结合此题，即（94-35×2）÷2=12只兔。二是“四头减足折半是鸡”，结合此题，即（35×4-94）÷2=23只鸡。

古人的这些解题思路既新颖又独特，学生领略到这些精妙的方法，学习到这么多古代数学的成就，一定会对古人的智慧称赞不已。通过思想和思想碰撞，学生或许会创造出一个又一个精妙的方法。

三、以传统数学文化内容丰富历史文化知识

古算题本身就蕴藏着丰富的历史文化信息，教学时增加经典的古算题可以让学生的数学思维和历史文化知识实现双丰收。

《九章算术》记载：“今有大夫、不更、簪袅、上造、公士，凡五人，共猎得五鹿，欲以爵次分之，问各得几何？”此题意为：由高到低五个不同爵位的人打猎，一共收获五只鹿，如果按5∶4∶3∶2∶1分配，问每个人各应分得多少只鹿。通过此题的学习，学生获取到按比例分配的知识（古人称之为衰分术），也了解了商鞅变法，了解了秦国奖励军功、鼓励杀敌求胜的二十级军功爵禄制度等方面的知识。

《孙子算经》记载：“今有九里渠，三寸鱼，头头相次。问鱼得几何？”意思是：今有9里长的水渠，鱼3寸长，这些鱼沿着水渠一条接一条的排开，问鱼有多少条。”学生在做这道古算题题时，需要了解当时的度量衡单位之间的换算。1里=360步，1步=5尺，1尺=10寸。因此鱼的总个数为：9×360×5×10÷3=54000（条）。

《九章算术》记载“今有粟一斗，欲为粝米，问为几何？”学生若做此题需了解古代的“粟米之法”。“粟米”泛指粮食，“法”是国家制定公民必须遵守的规则。“粟米之法”也就是以粟为基础而规定的粮食兑换的标准。古时候将粟的交换率定为50，粝米为30，粺米27，凿米24，御米21，小13.5，大54……现在我们再来看此题：今有粟1斗，要换成粝米。如果按粟米50可以换粝米30，问这1斗粟可以换粝米多少？学生可以用比例的知识解答：

设可以换x斗粝米。

50∶30=1∶x

x=0.6

0.6斗=6升。

四、以传统数学文化内容培养民族自豪感

几千年前我国就出现“洛书”，其中书写横、竖及对角线三个数之和都为15，使中国成为世界上最早研究幻方的国家。宋代数学家杨辉在他撰写的《续古摘奇算法》中列出了五至十阶的幻方。中国还是世界上最早使用十进位值制的国家。马克思在他的《数学手稿》一书中评价十进位值制记数法是“最美妙的发明之一”。著名的科学史学专家李约瑟博士曾对此给予很高的评价：“如果没有这种十进制，就几乎不可能出现我们现在这个统一化的世界了。”他还说：“总的说来，商代的数字系统比同一时代的古巴比伦和古埃及更为先进更为科学。”

中国还是最早使用分数、小数和负数的国家。两千年前的《九章算术》就出现了负数，印度直到七世纪才有，而西方国家直到十七世纪才接受负数。汉代徐岳所写的《数术记遺》记载，中国古代有筹算、珠算等14种计算方法。《孙子算经》专门记载算筹计数和运算的规则。北宋画家张择端所画《清明上河图》中的赵太丞家出现算盘的实物图。珠算经明代程大位的研究与推广，得到空前的发展，形成规范的珠算口诀。珠算还传播到东南亚、日本、朝鲜等许多国家。两千年前的《周髀》就记载了“周三径一”的研究成果。《隋书、历律志》记载祖冲之关于圆周率的研究成果：“圆周盈数三丈一尺四寸一分五厘九毫二秒七忽，朒数为三丈一尺四寸一分五厘九毫二秒六忽，正数在盈朒二限之间。”这一成果千年无人赶超。祖冲之还给出[355113]这个圆周率的渐近分数，让人钦佩的是分母在16500以内，精确度没有比这个分数更高的。

教学中增加这些数学史等传统数学文化内容，不仅可以让学生了解数学知识的来龙去脉和人类科学进步的历程，还可以学习其中蕴含的数学思想、方法等数学文化要素。学生了解我国古代的数学成就，既拓宽了知识面，又增强了民族自豪感。

参考文献：

[1] 竺斐君，李雪兰.链接数学文化丰富除法意义[J].辽宁教育，2019（15）.

[2]顾亚龙.以文“化”人——小学数学文化的育人视界[J].小学数学教师，2015（4期）.

（责任编辑：杨强）