图卷积神经网络基础图结构影响研究
2021-04-12李社蕾杨博雄刘小飞
李社蕾,周 波,杨博雄,刘小飞
(三亚学院 信息与智能工程学院,海南 三亚 572022)
1 引 言
自2012年以来,卷积神经网络(CNN)[1]在计算机视觉领域取得了巨大成功.它研究的对象限制在规则的欧式空间数据,但在处理现实问题过程中还会遇到大量非欧(Non-Euclidean)数据,许多重要的数据都以图或网络的形式存在,如社交网络、知识图谱、蛋白质相互作用网络、交通网络、引文网络、点云网络等.在图像匹配方面,也有很多研究将图像特征点的空间关系描述为图模型进行匹配算法的研究[2A].研究者开始将CNN在图结构上进行泛化,由于图结构数据不具备欧式数据天然的平移不变性,泛化过程中首先考虑的是如何在图结构上进行卷积运算.由此引申出了谱域方法和空间域方法两个研究方向;
在谱域方法方面,2014 Bruna[3]基于谱图理论提出了Spectral CNN模型,它将顶点域的卷积运算转化为傅里叶域的点积运算,从而定义了图信号傅里叶变换下的卷积算子,成功地将CNN泛化到了图结构上;Spectral CNN采用的卷积核包含N个自由参数,且需要显式地对图拉普拉斯矩阵进行特征分解,复杂度很高.2016 Defferrard[4]提出了ChebyNet模型,它引入参数化切比雪夫多项式卷积核,该模型中的参数为多项式的系数,且经过处理不需要再显式地对图拉普拉斯矩阵进行特征分解,复杂度大大降低.2017 Kipf and Welling[5]提出GCN模型,该模型的卷积核采用了ChebyNet卷积核的一阶多项式,进一步简化了运算,同时该卷积核产生了低频低波器的效果,使得模型性能得到了提升.上述卷积运算都是基于谱域展开的,属于全局的卷积核.2019 Xu[6]定义了基于谱图小波变换的卷积算子提出了GWNN模型,它采用了GCN的卷积核,利用图小波基实现了局部卷积.2019 Xu[7]提出了GraphHeat模型,在GCN和ChebyNet的基础上,通过对低频成分进行加强的方式引入了低通滤波卷积核.2019 Qu[8]将条件随机场与图神经网络结和提出了GMNN模型,利用条件随机场CRF对节点标签依赖关系进行建模;图神经网络通过非线性的神经元架构来学习节点的特征表示.2019 Yao Ma[9]EigenPooling研究了图卷积神经网络的池化方法,通过层次化的方式提取整个图的特征以实现图节点分类.

后续图卷积神经网络在各种图数据任务上进行扩展[14-18],都取得了不错效果.
综上所述,CNN在图结构泛化的过程中,主要集中在卷积和池化方面的研究,在基础图结构对模型的影响方面研究较少,研究基础图结构对模型的影响,在模型训练中有效地利用其结果有很重要的意义.基于此,本文从图卷积神经网络卷积核的角度研究了基础图结果对模型的影响,提出了一种利用图拉普拉斯矩阵特征值和特征向量的特性有效获取非连通图最大连通分量的算法,并用基于图半监督分类任务中的GCN、GAT和GMNN 3种重要模型在数据集Cora(最大连通分量)、数据集Citeseer(最大连通分量)上进行验证,节点分类准确率均实现了1%-4%的提升.
2 图傅里叶变换分析
在本节中,我们主要介绍图的相关定义、图傅里叶变换、图傅里叶变换卷积算子,并对图傅里叶基进行分析,研究图信号的平滑度、谱图分布与信号的关系,图信号的平滑度、图谱分布与基础图结构的关系,进一步研究基础图结构对训练模型的影响分析.
2.1 图相关概念
给定未加权无向图G={V,ε,W},该图由一组顶点V(|V|=N)、一组边ε和邻接矩阵W组成.vi∈V表示一个节点,eij=(vi,vj)∈ε表示两个节点i和j之间的边,邻接矩阵W∈N×N,其中:
定义图顶点上的信号或特征X:V→N×d,其中d为特征维度,度矩阵Dii=∑jWij.图拉普拉斯矩阵定义为L=D-W,对于图信号x∈N×d,图Laplacian作为其上的差分算子,可用于将图信号相对于图的总变化(total Variation:TV)[19]定义为:
其中,Ni={j}eij∈ε,因为L是对称矩阵,它有一组完备的正交特征向量{ul}l=0,1,…,N-1,这些特征向量对应一组非负实特征值{λl}l=0,1,…,N-1,满足Lul=λlul,l=0,1,…,N-1,对于连通图满足0=λ0<λ1≤λ2≤…≤λN-1:=λmax.
2.2 图傅里叶变换
传统傅里叶变换公式为:
(1)
可以理解为函数f的复指数展开式,复指数是一维拉普拉斯算子的本征函数:
(2)
与对时域信号的时间变化进行编码的傅立叶变换类似,图傅立叶变换(GFT:graph Fourier transform)被定义为对图信号中的空间变化进行编码.对于将图上的任意信号x∈,定义为x在图拉普拉斯特征向量方向上的展开:
即:
(3)
图信号逆傅立叶变换为:
即:

(4)
2.3 图傅里叶变换卷积算子
上面推导出了图傅里叶变换和图傅里叶逆变换的公式(3)和公式(4),由卷积定理可得图傅里叶变换卷积算子为[4]:
x*Gf=U(UTf)⊙(UTx)
(5)
其中,f∈N为图上的信号,⊙为元素级的Hadamard product.
2.4 傅里叶基信号分析
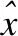
(6)
图信号在顶点域和谱图域中的表示如图1所示.其中,图1(a)为图信号x在64顶点Sensor网络的顶点域表示,图1(b)为图信号x在64顶点Sensor网络的谱域表示.

图1 图信号在顶点和图谱域中的表示Fig.1 Representation of graph signals in the vertex and graph domains
可以把拉普拉斯矩阵L的每个特征向量ul看作是图上的一个信号,它对应的特征值λl为其平滑度的度量,对于任意特征值λl有[20-23]:
在经典傅里叶分析中,公式(2)中的特征值{(2πξ)2}ξ∈带有特定的频率概念:ξ=0,对应的复指数本征函数为直流分量;ξ越接近0,相应的复指数本征函数越平滑;ξ离0越远,相应的复指数本征函数震荡越快.对图信号而言,图拉普拉斯特征值和特征向量提供了相似的频率概念,对于连通图,特征值λ0=0对应的特征向量在每个顶点处均等于恒定值较小特征值λl对应的特征向量在整个图上变化缓慢;较大特征值对应的特征向量震荡更快.图拉普拉斯特征值和特征向量的频谱特性如图2所示,其在的图2(a)、图2(b)中体现得都很直观.其中,图2(a)为8顶点path图各特征向量的可视化情况,图2(b)为8顶点Sensor网络部分特征向量的可视化结果.

图2 拉普拉斯特征向量在图顶点上的表示Fig.2 Representation of Laplace eigenvectors at graph vertices
2.5 图的平滑度、图谱分布与图信号的关系
如图3所示,两幅图的结构是完全相同的,但图上的信号不同.左边图上的信号比较平滑,其TV(x)=xLxT=0.48,所对应的傅里叶变换谱中,能量主要在低频成分;而右边图上的信号震荡较快,其TV(x)=xLxT=4.18,所对应的傅里叶变换谱中,低频成分减少,包含了大量中高频率成分.
2.6 图信号的平滑度、图谱分布与基础图的关系
图拉普拉斯矩阵编码了基础图的连接性,并用于定义图傅里叶变换(通过图拉普拉斯特征向量)和平滑度概念,图信号平滑度、 傅里叶谱分布和基础图结构也有关系, 信号平滑度、图谱含量与基础图的关系如图4所示.上面3个图中,图信号一样,但图结构各不相同,可以看出图的连通性越弱,傅里叶谱越趋近低频方向.

图3 图的平滑度、图谱分布与信号的关系Fig.3 Relationship between the smoothness of the graph,spectral distribution and the signal

图4 基础图与图信号的平滑度、图谱分布的关系Fig.4 Relationship between the basic graph structure,the smoothness and spectral distribution
2.7 基础图结构对训练模型的影响分析
本部分从谱域图卷积神经网络模型的卷积核作为切入点,研究图结构在模型的影响:
1)Spectral CNN[3]中定义了自由卷积核:

(7)
公式(7)可得:
(8)
公式(8)结合公式(5)得:
(9)
2)ChebyNet[4]提出了参数化卷积核:
(10)
ChebyNet中图信号的卷积运算定义为:

(11)
由公式(11),可以看出公式(10)定义的卷积核可以聚合了一到k阶邻居的特征.
3)GCN[5]只取ChebyNet一阶多项式近似,即,K=2,并且令α=α0=-α1.图卷积定义为:
(12)
GCN模型进一步简化了运算,并且该模型的卷积核起到了低通滤波器的作用.
4)GraphHeat[7]从低通滤波的角度出发,定义了基于热核的低通滤波卷积核,
热核定义为:
f(λi)=e-sλi

其中,θk为参数,对于信号x图卷积可表示为:

取,y=(θ0I+θ1e-sL)x
(13)
3 数据集最大连分量提取算法
3.1 数据集图结构分析
对Cora、Citeseer及Pubmed 3个基本数据集进行分析.图6(a)为Pubmed图结构的可视化结果;6(b)显示了Pubmed图拉普拉斯矩阵最小的50个特征值的分布情况,可以看出只有一个“0”特征值,所以Pubmed图结构为连通图.图7(a)为Cora图结构的可视化结果,图8(a)为Citeseer图结构的可视化结果,两者均为非连通图,包含了一些小连通分量,有的连通分量只有1个节点或2-3个节点,中间的最大分量包含了绝大多数节点;这些小连通分量因聚合有限,包含的图结构信息有限,在对编码了图结构和图信号的特征进行训练时,很难保证其准确性;下面考虑去掉其小连通分量,只对其最大连通分量进行训练.
3.2 非连通图获取最大连通分量算法
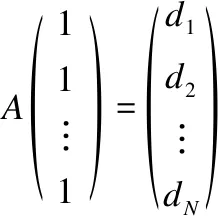
则:
(14)
如图5所示.

图5 两个8节点Sensor网络的图拉普拉斯矩阵“0”特征值对应的特征向量分布情况
如图6所示,数据集Pubmed图拉普拉斯矩阵只有一个“0”特征值,其图结构为连通图.
如图7所示,数据集Cora中共有2708个节点,其最大连通分量包含2485个节点,剩余223个节点分布在70多个小连通分量上.利用该方法成功获取到数据集Cora图结构的最大连通分量.
如图8所示,数据集Citeseer中共有3327个节点,其最大连通分量包含2120个节点,剩余1205个节点分布在众多小连通分量上.利用该方法成功获取到数据集Citeseer图结构的最大连通分量.

图6 数据集Pubmed可视化结果.(a)为Pubmed原始图结构可视化结果,(b)为Pubmed图结构拉普拉斯矩阵前50个特征值的分布Fig.6 Visualization results of data set Pubmed.(a)is the visualization result of the original graph structure of Pubmed,and(b)The distribution of Pubmed graph Laplace matrix first 50 Eigenvalues

图7 数据集Cora可视化结果.(a)为Cora原始图结构可视化结果,(b)为Cora最大连通分量可视化结果Fig.7 Visualization of data set Cora.(a)is the visualization result of the original graph structure of Cora,and(b)is the visualization result of the maximum connected component of Cora

图8 数据集Citeseer可视化结果.(a)为Citeseer原始图结构可视化结果,(b)为Citeseer最大连通分量可视化结果Fig.8 Visualization of data set Citeseer.(a)is the visualizationresult of Citeseer original graph structure,and(b)is the visualization result of Citeseer maximum connected component
4 实验结果
本文采用数据集(Cora、Citeseer)最大连通分量分别在GCN、GMNN、GAT 3种模型进行了验证,为了对比方便采用与GCN、GMNN、GAT原模型相同的所有超参数,训练集、验证集及测试集得节点数分别为140、500和1000.其中,数据集Cora及最大连通分量的统计信息如表1所示.

表1 数据集Cora及最其大连通分量的统计信息Table 1 Statistical information of dataset Cora and its maximum connected components
实验结果分别与GCN、GMNN、GAT 3个模型的结果进行对比,节点分类结果如表2、表3所示.

表2 数据集Cora节点分类结果(%),[*]意味着结果来自于对应的论文.Table 2 Node classification results of data set Cora(%).[*] means the results are taken from the corresponding papers

表3 数据集Citeseer节点分类结果(%),[*]意味着结果来自于对应的论文Table 3 Node classification results of data set Citeseer(%).[*] means the results are taken from the corresponding papers
由图7(a)、图8(a)可知Cora 和Citeseer的图结构均为非连通图,包含了一些小连通分量,部分连通分量只有1个节点或2-3个节点,图的最大连通分量包含了绝大多数节点;这些小连通分量因在邻域特征聚合的过程中,因为没有邻居节点或者极少的邻居节点,无法进行有效的特征学习,很难保证其分类准确性;去掉其小连通分量后,只对其最大连通分量进行训练,在邻域特征聚合的过程中能够聚合到邻域的特征信息,就可以需学习到更有效的特征表示,从而提高分类准确率.
实验结果结合GCN、GMNN、GAT 3种模型在数据集(Cora、Citeseer)上进行了验证,3种模型的节点分类准确率都得到了1%-4%的提升.
5 结论和展望
由于图的非连通性,部分小连通分量只有2到3个节点,这些小分量很难有效聚合邻域特征进行训练,利用同时编码了图结构和图信号的特征训练这些小分量中的节点也是没有实际意义的,利用它们的图结构聚合邻域特征得出的训练结果缺乏可解释性.本文研究了利用图拉普拉特征值和特征向量的特性获取图结构最大联通分量的方法,在数据集(Cora、Citeseer)上有效获取了图结构的最大连通分量,并利用GCN、GMNN、GAT 3种模型进行节点分类,实验表明本文基于最大连通分量的训练是有意义的,但仍有很大的提升空间;由此可知在训练过程中基础图结构作用发挥有限,如何更有效地编码图结构信息,让图结构更有效地参与训练仍是值得深入研究的问题.
