无信号交叉口车辆调度方法研究

侯运锋，龚朝晖

(上海理工大学 光电信息与计算机工程学院，上海 200093)

1 引 言

对交通系统的建模和控制是避免交通拥堵和减少交通事故的关键.在车路协同环境下，智能交通系统，特别交叉口的车辆通行控制方法已经成为各国的研究重点.经过多年的发展，产生了诸如美国的智能驾驶，欧盟的智能交通系统(Intelligent Transportation Systems，ITS).智能交通系统基于先进的传感器和信息通信等技术，实现车辆与车辆、车辆与道路之间的信息交互，保证车辆在复杂的交通环境下的行驶安全，对道路交通实施主动控制.

Pandit等[1]基于车路信息交互提出了交叉口车辆的在线调度算法(Oldest Job First，OJF).该算法利用图论对路口的交通动作进行建模.交叉口车辆所有的交通动作表示为图的一个顶点.若两个动作发生冲突，则在其对应顶点之间连接一条直线.互相发生冲突的车辆不能同时调度.由于OJF每次只处理最先到达交叉口的车辆，所以信号灯的切换过于频繁，难以在实际中应用.为了提高交通运输效率，赵文天等[2]提出(Frame-based Traffic Scheduling，FTS)算法，该算法采取和OJB相同的车辆调度模式，不同的是FTS将一个时间段内路口的车辆积攒到一起处理，有效地减少了相位的切换次数和车辆的等待时间.Kamal等人[3]基于车路协同技术，根据当前时刻各个路段上的车辆行驶状态在线优化信号灯相位的时间配比，并提前一个周期广播给路段上所有车辆，车辆根据广播调整自身速度，以最短停车时间通过路口.另外，随着人工智能技术的发展，基于智能算法的信号配时优化技术也得到了长足发展[4，5].

传统信号灯控制方式[1-5]同一时刻只允许互不冲突相位上的车辆通过.为确保安全，每个相位最后几秒通常设置为黄灯时间.在黄灯时间路段上的所有车辆都不被允许驶入交叉口.相位之间的频繁切换会导致信号周期单位时间内黄灯时间占比增加，从而降低交叉口的通行能力.

上官伟等[6]在车路协同环境下，设计了基于时延Petri网(Petri Net，PN)的无信号交叉口控制方法.该方法依据时延PN模型，将交叉口当作车辆行驶的共享区域，以最小化交叉口车辆消散时间为优化目标，由路侧单元的中央控制器给不同路段上的车辆分配路权.该算法认为交叉口为一个单独的路权，为了保证行驶安全，所有与当前正在通过交叉口的车辆行驶轨迹发生冲突的车辆都不被允许驶入交叉口.这在一定程度上浪费了有限交叉口物理空间资源.

Febbraro 等[7-10]将交叉路口细分为不同的空间区域.每个空间区域最多容纳一辆车辆.每一个空间区域采用一个PN单元来建模.空间区域的最大车容量为描述该空间区域库所的令牌数量.Wang等[11]提出了一种双模块交叉口PN表示方法，其中第一个模块将交叉口细分为不同的空间区域，然后对其进行建模.每个空间区域同样最多只能容纳一辆车辆.第二个模块对交叉口的交通信号系统进行建模.然后，将两个模块耦合在一起实现对交叉口车辆通行的控制.在该模型中，作者认为从西到北的左转车辆和从东到南的左转车辆属于同一相位的不同阶段，需要分别执行.然而，现实中相向行驶的左转车辆可以共享同一空间区域而不发生碰撞.显然，基于划分空间的车辆控制方法中[7-11]每个空间区域最多只能容纳一辆车辆的设定影响了交叉口的车辆吞吐能力.

针对上述问题本文在车路协同模式下提出了一种无信号交叉口微观建模方法.该方法将交叉口划分为不同的空间区域，并把不同的区域设为不同的路权资源，智能车辆通过不同的空间区域需要向路侧单元申请相应的路权使用权，路侧单元根据车辆行驶信息实时控制车辆的通行.不同于之前的工作[7-11]，本文认为每个路权的最大容量要根据车辆的行驶方向实时确定.例如，同一相位上的两辆相向而行的左转车辆的行驶轨迹不会发生冲突可以同时占用一个路权.然而，不同相位上的一辆左转车辆和一辆直行车辆的行驶轨迹会发生冲突，为保证安全，这两辆车不能共享同一个路权.路权资源要根据到达该资源车辆的行驶方向来确定其最大车容量.在此基础上，构建无信号交叉口资源调度模型，以最大化交叉口的通行效率为目标，在线计算无交叉口车辆调度方案.所设计方案在保证车辆通行安全性的同时充分考虑了路权资源最大容量的动态变化特性，力求达到“见缝插针”的效果.与此同时，基于无信号交叉口物理空间的车辆调度方式不存在由于相位切换而导致的黄灯时间占比增加的问题，进一步提升了交叉口车辆吞吐能力.

2 研究对象

2.1 交叉路口

本文选用如图1所示双向两车道交叉口作为研究对象，所阐述方法同样适用于双向四车道交叉口和T型交叉口.图1所示交叉口一共有8条路段，分别为路段1～8.模型构建的基本思想是将交叉口物理空间划分为互不相交的路权.如图1所示，交叉口被划分为5个互不相交的路权a、b、c、d、e.车辆通过交叉口的过程中不可避免地要占用某些路权.例如，从路段1直行驶向路段5的车辆需要依次占用路权a、d.从路段3左转进入路段5的车辆需要依次占用路权b、e、d.从路段2右转进入路段8的车辆要占用路权c.不同的车辆在通过交叉口的过程中可能会占用相同的路权，例如，从路段1直行驶向路段5与从路段4直行驶向路段8都需要占用路权d.为了保证车辆行驶的安全，需要定义每个路权的最大车容量.

图1 本文所讨论交叉口结构图Fig.1 Intersection discussed in this paper

本文认为各个路权的最大车容量是动态变化，每个路权的最大车容量要根据驶入车辆的行驶方向动态确定.交叉口相向行驶的左转车辆不会发生碰撞，因而，从路段1左转驶向路段8的车辆和从路段2左转驶向路段7的车辆可以同时共享路权a、e、c.这时候，路权a、e、c的车容量可设为2.同理，从路段3左转驶向路段5的车辆和从路段4左转驶向路段6的车辆可以同时共享路权b、e、d.此时路权b、e、d的车容量为2.其他情况下，路权a、b、c、d、e同一时刻最多容纳1辆车辆.例如，若路权a被一辆由路段1或者路权b驶入的直行车辆占用，那么此时其他任何车辆不被允许驶入路权a，路权a的最大车容量为1.

2.2 控制模式

目前智能无信号交通控制方式主要分为中央控制站控制模式和车车协同控制模式，本文采用中央控制站控制模式，中央控制站控制模式中车辆主要和路侧智能设备进行通信，避免了不同车辆之间的大量信息交互，从而在一定程度上降低了系统对无线通信网络的要求.

本文所考虑的无信号交叉口控制系统主要由3部分组成：

1)自治车辆：当具有智能车载系统的车辆进入路口感应区域时，车辆能够将自身状态信息实时发送给智能路侧系统，并且能够实时接收智能路侧系统的指令信息.

2)智能路侧单元：作为交叉口的“大脑”，与交叉口区域内的自治车辆进行信息交互，获取车辆的实时状态信息；路侧单元基于所构建模型，利用优化算法，得到最优车辆通行序列，实时向车辆分配交叉口各个区域的使用权，引导车辆通过交叉口.

3)协同信息交互系统：自治车辆和智能路侧系统的信息传输载体.

3 交叉口模型

3.1 有限自动机

智能交通系统具有高度并发性、资源共享性以及动态性，而在描述系统异步性和并发性方面，有限自动机具有显著的优势.本文利用有限自动机构建无信号交叉口路权调度模型.所构建模型考虑了路权最大容量的动态变化特性，充分地利用了有限的交叉口物理空间.

有限自动机(Finite States Automaton，FSA)可以表示为一个5元组G=(X,E,f,Γ,x0)，其中，X是有限状态集合；E是有限事件集合；f:X×E→X是状态激活函数；Γ是活跃事件函数，任给x∈X，Γ(x)={σ∈E:f(x,σ)!}，其中，f(x,σ)!表示f(x,σ)有定义；x0是初始激活状态.E*表示由E中元素组成的事件发生序列集合.根据事件是否可控，E被分割为可控事件集合Ec和不可控事件集合Euc，即E=Ec∪Euc.f的定义阈按以下方式从E扩展至E*：对于空事件发生序列ε，f(x,ε)=x；任给事件发生序列s∈E*和事件σ∈E，f(x0,sσ)=f(f(x0,s),σ).

事件的发生必须满足某些限制条件.将事件发生条件函数引入到FSA模型中，往往可以为系统的模拟和分析提供便利.本文对FSA模型做进一步拓展，定义了普遍意义下的FSA(Generalized Finite States Automaton，GFSA)模型.GFSA可以描述为6元组G=(X,E,f,Γ,x0,c)，其中，(X,E,f,Γ,x0)是一个普通FSA模型，c:E→{0,1}是事件发生条件函数.给定x∈X和σ∈E，其中，f(x，σ)!若当前时刻状态x处于激活状态，并且事件σ满足发生条件，即c(σ)=1，那么，事件σ允许发生，否则，不被允许发生.

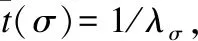
3.2 模型构建

为了更好地表述模型的构建过程，对模型中所使用符号做如下解释：数字1-8表示路段1～8；字母a、b、c、d、e分别表示路权a、b、c、d、e；字母s、r、l分别表示直行、右转、左转车辆.事件σxzk，其中，x，z=1，…，8，a，…，e，k=l，s，r，表示一辆k类型车辆由x驶入z，比如，事件σ1as表示一辆直行车辆由路段1驶入路权a；事件σael表示一辆左转车辆由路权a驶入路权e；事件αxk，其中，x=1，…，4，k=l，s，r，表示一辆k类型车辆由路段x到达交叉口，比如，事件α1s表示一辆直行车辆由路段1到达交叉路口.

本文构建交叉口模型的过程分为4步：1)构建各个路权的FSA模型；2)构建交叉口各个方向上的车辆到达FSA模型；3)交叉口FSA模型由各个路权FSA模型和交叉口各个方向上的车辆到达FSA模型并行产生；4)定义交叉口FSA模型的事件发生条件函数，构建交叉路口的GFSA模型.

3.2.1 所有路权的FSA模型

路权a～e的FSA模型分别如图2(a)-图2(e)所示，分别记做G1～G5.G1中所有状态的具体定义如下：状态0表示路权a空置；状态1表示路权a被一辆由路段1驶入的左转车辆占用；状态2表示路权a被一辆由路权e驶入的左转车辆；状态3表示路权a被一辆由路段1驶入的左转车辆和一辆路权e驶入的左转车辆同时占用；状态4表示路权a被一辆由路段1驶入的直行车辆占用；状态5表示路权a被一辆由路段1驶入的右转车辆占用；状态6表示路权a被一辆由路权b驶入的直行车辆占用.

由图2(a)可知，模型G1的初始激活状态为0，路权a空置.若此时一辆左转车辆从路段1驶入a，伴随事件σ1al的发生，系统激活状态1，此时允许一辆左转车辆从e驶入a，除此之外，其他占用路权a的行为都会导致车辆相撞而被严格禁止.假设此时一辆左转车辆从e驶向a，伴随着事件σeal的发生，系统激活状态3.此时路权a被两辆左转车辆同时占用，其他车辆不被允许驶入路权a.接下来，如果一辆车辆离开a进入e，伴随着事件σacl的发生，路权a中只剩下一辆由路权e驶入的左转车辆，系统激活状态2.接下来若由路权e驶入路权a的车辆离开a进入路段7，便随着事件σa7l发生，系统激活初始状态0，路权a空置.当系统状态3处于激活状态时，若路权a中一辆车辆离开a进入路段7，便随着事件σa7l的发生，a中只剩一辆由路段1驶入的左转车辆，系统激活状态1.此时若这辆左转车辆离开a前往e，路权a空置，系统激活初始状态0.

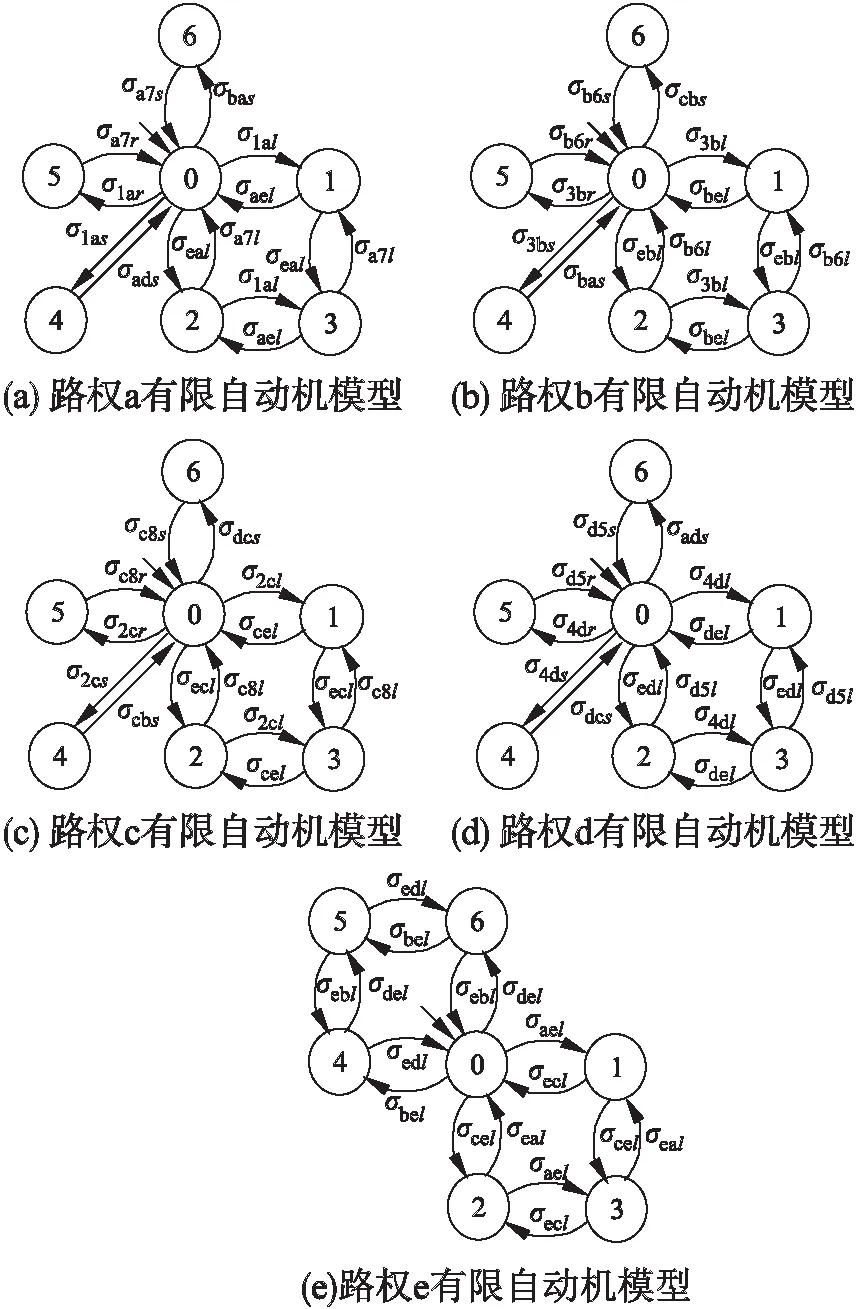
图2 路权a、b、c、d、e的FSA模型Fig.2 FSA models for section a、b、c、d、e

另一方面，在初始状态0，事件σ1as、σ1ar、σbas发生后，系统分别激活状态4、5、6.除非接下来这些车辆离开a进入接下来的路权或路段，其他任何车辆不被允许驶入a.由于路权b、c、d的FSA模型和G1具有较强的可类比性，为了更加简洁，不再分析G2～G4的状态演化过程.

G5中所有状态的具体定义如下：状态0表示路权e空置；状态1表示路权e被一辆由路权a驶入的左转车辆占用；状态2表示路权e被一辆由路权c驶入的左转车辆占用；状态3表示路权e被一辆由路权a驶入左转车辆和一辆由路权c驶入的左转车辆同时占用；状态4表示路权e被一辆由路权b驶入的左转车辆占用；状态5表示路权e被一辆由路权b驶入左转车辆和一辆由路权d驶入的左转车辆同时占用；状态6表示路权e被一辆由路权d驶入的左转车辆占用.

区域e可以同时容纳一辆从路权a和路权c，或者路权b和路权d驶入的车辆.但是，当一辆来自路权a或者路权c的车辆驶入区域e时，路权b和路权d的车辆被严格禁止驶入路权e(如图2(e)所示，σbel和σdel在状态1、2、3没有定义).同理，当一辆来自路权b或者路权d的车辆驶入路权e时，路权a和路权d的车辆被严格禁止驶入路权e(σael和σcel在状态4、5、6没有定义).

3.2.2 交叉口各个方向上的车辆到达FSA模型

图3(a)-图3(d)模拟了路段1～4上的车辆到达交叉口的过程.图3(a)-图3(d)所示模型分别记做G6～G9.

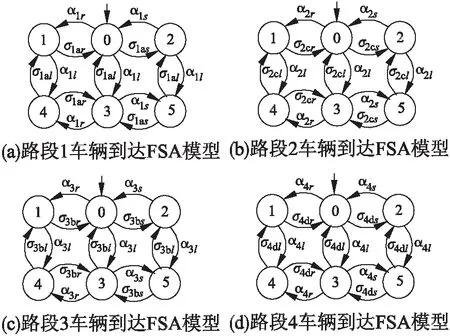
图3 交叉口各个方向上的车辆到达FSA模型Fig.3 Vehicle arrival models for the intersection

以图3(a)为例，若路段1上一辆直行车辆到达交叉口，便随着事件α1s的发生，系统状态2激活.由图1可知，此时路段1上的右转、直行车辆只能排在这辆直行车辆之后，等到这辆直行车辆驶入区域a，即事件σ1as发生后，才能继续到达交叉口.然而此时路段1上的左转车辆可以不受直行车辆的影响驶入左转车道，因此事件α1l在状态2有定义.当一辆左转车辆到达交叉口后，便随着事件α1l的发生，系统状态5激活.在左转车辆驶入区域a之前，即事件σ1al发生之前，路段1上的其他左转车辆不能到达交叉口.

同理，当初始状态0处于激活状态时若一辆右转车辆到达交叉口，伴随着事件α1r的发生，系统状态1激活.此时可能存在一辆左转车辆到达交叉口.若一辆左转车辆到达交叉口，伴随着事件α1l的发生，系统状态4激活.

另外，当初始状态0处于激活状态时若一辆左转车辆到达交叉口，伴随着事件α1l的发生，系统状态3激活.此时可能存在一辆右转或者直行车辆到达交叉口.若一辆右转车辆到达交叉口，伴随着事件α1r的发生，系统状态4激活.若一辆直行车辆到达交叉口，伴随着事件α1s的发生，系统状态5激活.

G6中所有状态的具体定义如下：状态0表示路段1上没有车辆到达交叉口；状态1表示路段1上一辆右转车辆到达交叉口；状态2表示路段1上一辆直行车辆到达交叉口；状态3表示路段1上一辆左转车辆到达交叉口；状态4表示路段1上一辆左转车辆和一辆右转车辆到达交叉口；状态5表示路段1上一辆左转车辆和一辆直行车辆到达交叉口.由于G7～G9和G6具有较强的可类比性，为了更加简洁，不再分析G7～G9的状态动态演化过程.

3.2.3 交叉口FSA模型

各个FSA之间既相互独立又互相影响，它们通过互相之间的共同事件相互作用.例如，σael是G1和G5共同定义的事件，若此时G1和G5的激活状态分别为1和0，σael发生后G1和G6的激活状态变为0和1.同理，σ1al是G1和G6共同定义的事件，若此时G1和G6的激活状态分别为0和3，σ1al发生后G1和G6的激活状态变为1和0.另外，α1s只在G6中有定义，若此时G6的激活状态是0，α1s发生后只会导致G6的激活状态变为2，其他FSA模型的状态不会受影响.

为了将G1～G9耦合在一起，引入如下并行操作[12].给定H1=(Q1,∑1,δ1,Γ1,q01)和H2=(Q2,∑2,δ2,Γ2,q02)，H1和H2并行产生H=Ac(Q1×Q2,∑1∪∑2,δ,Γ1‖2,(q01,q02))，其中，任给(q1,q2)∈Q1×Q2和σ∈∑1∪∑2，若σ∈Γ1(q1)∩Γ2(q2)，那么，δ((q1,q2),σ)=(δ1(q1,σ),δ2(q2,σ))；若σ∈Γ1(q1)/∑2，那么，δ((q1,q2),σ)=(δ1(q1,σ),q2)；若σ∈Γ2(q2)/∑1，那么，δ((q1,q2),σ)=(q1,δ2(q2,σ))；其他情况，δ((q1,q2),σ)没有定义.Ac表示取有限自动机由初始状态可到达部分.

交叉口FSA模型由G1～G9并行产生.正式地，基于有限物理空间的交叉口FSA模型为：

G=G1‖G2‖…‖G9=(X，E，f，Γ，x0)

任给x=(x1,x2,…,x9)∈X,x1～x5，分别表示当前时刻路权a～e所处状态，x6～x9分别表示当前时刻路段1～4上的车辆到达交叉口的情况.Γ(x)可以理解为当前时刻可以选择触发而不会导致车辆相撞的事件集合.例如，任意给定激活状态x=(1,0,0,0,0,3,0,0,0)，此时路段1上有一辆左转车辆到达交叉口，另外路权a被一辆从路段1上驶入的左转车辆占据.若触发事件σael∈Γ(x)，占用路权a的左转车辆从路权a驶入路权e，系统激活状态(0,0,0,0,1,3,0,0,0).相反，若选择触发事件集合Γ(x)以外的事件，例如σ1al，则会导致两辆车辆在路权a相撞.由于我们不能控制车辆是否到达交叉口，因而系统的不可控事件集合为Euc={σis,σir,σil：∀i=1,2,3,4}，可控事件集合Ec=E/Euc.

3.2.4 交叉口GFSA模型

FSA模型可以表达系统所访问的状态序列和导致这些状态转换的相关事件，但却不能表达系统何时进入特定的状态或系统保持这种状态的时间.然而，在模型的控制过程中我们常常需要考虑事件序列发生时间的长短，因此，在交叉口的GFSAG=(X,E,f,Γ,x0,c)模型中我们定义了所有事件发生需要满足的时钟条件.

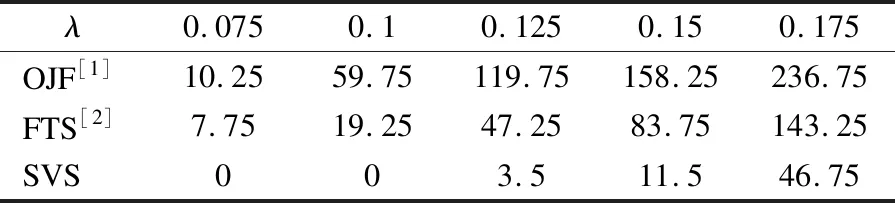
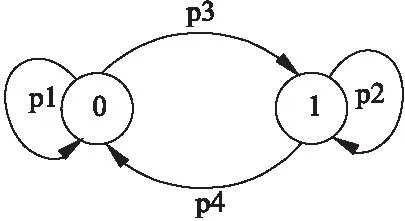
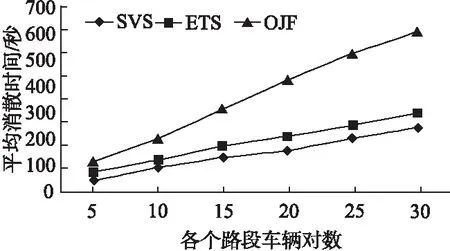
事件发生条件函数c定义如下：以事件σads和σ1as为例，不难发现，只有直行车辆从路段1完全驶入路权a后，才有可能继续从路权a驶入路权d，所以说事件σads只有在事件σ1as发生结束后才可能被触发.任意给定事件σ∈E，定义π(σ)为事件σ最近一次触发距离当前时刻的时长.若σ未曾发生，则定义π(σ)=0.根据 3.1节的定义，t(σ)为事件σ发生所需时间.若σ未曾发生，定义t(σ)=-∞.事件σads的发生条件函数可以定义为：如果π(σ1as)≥t(σ1as)，则c(σads)=1；否则，如果π(σ1as)

表1 可控事件发生条件Table 1 Occurrence conditions for controllable events

事件的σ1as发生条件则要根据路段1上车辆到达交叉口情况来决定.具体地，事件σ1as的发生条件函数定义为：如果π(α1s)≥t(α1s)，则c(σ1as)=1；如果π(α1s)

3.3 死锁状态

在无信号交叉口的控制过程中要防止死锁的出现.所谓死锁是交叉口当前车辆所处位置互相阻碍对方前行的一种状态.例如，若此时路a权被一辆由路段1驶入的直行车辆占用，路权b被一辆由路段3驶入的直行车辆占用，路权c被一辆由路段2驶入直行车辆占用，路权d被一辆由路段4驶入的直行车辆占用.在当前情形下，这4辆车辆互相阻碍对方的前进方向都无法驶离当前位置，因而形成死锁.定义1正式地给出了死锁状态的定义.

定义1.任意给定x=(x1,x2,…,x9)∈X，如果不存在s∈E*使得f(x,s)=x0，则称状态x为死锁状态.

由定义1可知，死锁状态是一些不能返回初始状态的状态.直观上，当系统到达这些状态时，不存在通行序列使当前交叉口通行车辆驶离交叉路口.在控制交叉口车辆通行的过程中，死锁状态是要严格禁止到达的.

4 优化控制

本节设计控制器调节交叉口车辆的通行次序.不失一般性，可控事件σ∈Ec的发生条件记为π(σ′)≥t(σ′)，事件集合E记为E={σ1,σ2,…,σm}.设第k步，系统所处状态、事件σ最近一次发生距离当前时刻时长、事件σ最近一次发生所需时间、选择触发的事件分别为xk、πk(σ)、tk(σ)、αk，定义Ψk=Ψ(xk,πk(σ1),…,πk(σm),tk(σ1),…,tk(σm),αk)为触发事件ak需要等待的时间.以下算式计算得出了将当前到达交叉口的车辆和交叉口内的通行车辆完全排空所耗费时间最少的车辆通行序列.

(1)

s.t.(∀i=0,1,…,nk)ak+i∈Ec

(2)

f(xk,akak+1…ak+nk)=x0

(3)

其中，迭代过程为：

∀z=k+1,k+2,…,k+nk,Ψz=Ψz-1+τz-1

(4)

(5)

对所有σ∈E，

(6)

(7)

xz=f(xz-1,az-1)

(8)

需要指出的是，虽然我们计算了接下来nk步内的最优车辆通行序列，然而该序列是基于当前时刻交叉口的车辆情况计算得出的，在执行上述序列的同时可能存在新的车辆到达交叉口(不可控事件的发生).因而，实际中我们只执行所计算最优通行序列中的第1步，在第1步执行结束后，基于系统最新状态和参数，再次执行上述优化过程，计算下一步的通行控制策略.

5 实验与分析

5.1 实验设置

本文的仿真环境为MATLAB，仿真精度为1s，也就是说系统每隔1s更新一次控制策略.本文假定1)各个驶向交叉口方向上单位时间内的车辆到达数符合泊松分布；2)各个方向上的到达车辆右转、直行、左转的概率分别为0.2、0.4、0.4；3)所有事件的发生时间符合参数为0.5的指数分布.表2给出了事件发生时间概率分布关系.

表2 事件发生所需时间的概率分布关系Table 2 Distribution of the time taken to execute an event

5.2 仿真实验

本节展示了所设计基于交叉口有限物理空间的车辆调度算法(Spatial-based vehicle scheduling，SVS)在仿真周期内的车辆排队数，以及将有限车辆全部调度完毕的耗费时间，并与目前交通控制系统中信号灯交通控制方式进行对比分析.

首先考虑各个驶向交叉口方向上单位时间内的车辆到达数符合数学期望一致的泊松分布的情况(平衡车流).不失一般性，假设数学期望为λ.

图4 不同λ取值下车辆排队长度的比较Fig.4 Queue length with different values of λ

图4给出了当λ取不同数值时1200s内交叉口车辆排队总和.在图4中每隔10s记录一次车辆排队数据，第10次取样数据即为100s时交叉口车辆排队长度总和.如图4所示，当λ=0.1,0.125,0.15时，SVS能够确保交叉路口的排队车辆不高于25辆，显示出了较强的鲁棒性.当λ=0.175时，随着时间的增加，交叉口出现了大量的排队车辆.这说明基于单个交叉口的控制难以控制相对较大的车流量.此时需要多个相邻交叉口、路段之间的协同控制.接下来，在平衡车流下测试了OJF算法[1]、FTS算法[2]和SVS算法在不同车流量下的表现.

表3 3种算法在平衡车流下车辆排队长度比较Table 3 Comparison of queue lengths in three algorithms

表3给出了平衡车流下，在3种算法控制下交叉口车辆排队数随着参数 的变化过程.所有数据为4次实验的平均值，每次实验仿真时长为10分钟.通过表3可知，在不同车流量下，本文提出的SVS算法仿真周期内排队车辆明显更小；特别是当λ=0.1,0.125,0.15时，SVS较OJF和FTS显示出较强的鲁棒性.这是因为，当车流量较小时，OJF算法和FTS算法需要多次切换相位以满足控制需求，从而损失更多的时间(黄灯时间).当λ=0.175时，FTS和SVS仿真周期内的排队车辆都呈现大幅度增长.当交叉口的到达车辆趋向饱和时FTS相位切换的次数减小，然而，由于OJF每次只处理一辆车辆，其相位切换次数不会随着车流的变化而发生明显的变化，相比FTS由于相位的频繁切换而导致的损失时间更大，因而，仿真周期内OJF的表现明显逊色于FTS和SVS.

图5 马尔科夫模型Fig.5 Markov model

上述实验认为各个路段的车辆到达情况一致.然而在现实中每个路段的车辆到达情况随着时间的变化会发生相应变化.为描述这种变化，引入如图5所示马尔科夫模型.模型一共有两个状态，系统状态的转移概率分别为p1、p2、p3、p4.假设系统状态的初始状态为0.模型下一步的状态只与系统当前步所处状态相关，而与之前所处状态无关，并且状态转移概率不受时间的影响.假设当模型处于状态0时，车辆到达随机数满足数学期望为λ1的泊松分布，处于状态1时，满足数学期望为λ2的泊松分布.由于状态在仿真过程的每一步都可能发生转移，考虑到车辆的到达率在短时间内发生改变的概率比较低，我们设定如下状态转移概率：p1=0.8、p2=0.8、p3=0.2、p4=0.2.

表4 参数λ1和λ2的取值Table 4 Values of λ1 and λ2

表5 3种算法在非平衡车流下车辆排队长度比较Table 5 Comparison of queue lengths in three algorithm

表4给出了一些较大车流量下的参数取值.表5展示了当参数λ1和λ2的取表4所列类别的数值时，在3种算法的控制下，10min的仿真周期内交叉口的车辆排队情况.总体来讲SVS的表现明显要优于OJF和FTS.OJF和FTS在非平衡车流下的表现要劣于其在平衡车流下的表现.除类别3外，SVS显示出很好的车辆调度效果，对非平衡车流表现出很好的鲁棒性.在类别3，SVS出现一定的不稳定性，但相对OJF和FTS，仍然显示出了很好的控制效果.接下来我们测试当路段1～4的车辆排队数为5、10、15、20、25、30时，3种算法将车辆调度完毕所消耗时间.实验结果如图6所示.

当路段1～4的车辆排队数为5、10、15、20、25、30时，SVS将所有车辆消散的平均耗时相比于FTS控制方法分别减少了43.1%、22.4%、25.7%、26%、19.1%和17.8%，相比于OJF控制方法分别减少了61.5%、53.3%、58%、63%、60.7%和59.5%.显然，本文所提出SVS算法的平均车辆消散时间相比于OJF和FTS有比较明显的减少.

图6 3种算法车辆调度时间对比Fig.6 Comparison of scheduling time among three algorithms

6 总 结

智能交通是未来交通系统的发展趋势，车路协同技术是是发展智能交通系统的重要一环，其目标是实现自治车辆和智能路侧设备之间的协同关系，确保交通系统的安全高效.本文就车路协同技术的问题之一，无信号交叉口的车辆调度方法展开了相应研究.为实现车辆对交叉口有限物理空间的最大利用，将交叉口划分为不同的区域资源，并建立相应的资源调度模型，以最大化通行效率作为优化目标建立目标函数，求解得到车辆的最优通行次序.实验结果显示，较传统有信号控制方案，新方案在保证车辆行驶安全的同时，极大地提高了车辆通过交叉口的效率.

本文集中研究单个交叉口的车辆通行控制方法，接下来将考虑更加复杂的情况，对多个交叉口和道路之间的车辆协同调度方法展开研究.