从数形结合思想切入初中数学核心素养的培养
2021-04-06归爱琴
归爱琴

【摘 要】在新课程改革的背景下,初中数学教学过程当中也特别注重学生核心素养的培养,通过培养学生数学核心素养,可以促进学生综合能力的提升,让學生在学习的过程当中善于发现问题、分析问题,对问题进行探究,进而解决问题。而在学生数学核心素养培养的过程当中,其数形结合思想的应用是非常重要的,它可以将数与形之间,进行有效的结合和互变,简化数学问题,从而提高学生学习数学的效率。
【关键词】数形结合思想;初中数学;核心素养;培养
数和形自古以来就是数学当中的两大主要研究对象,通过数形的有效结合,可以将数量上的关系与相应的几何图形进行相关联,进而探索出问题的答案。在数与形的结合过程当中,可以拓展学生的数学思维,提高学生对数学知识的应用能力,从而促进学生数学学科核心素养的形成。所以在初中数学教学过程当中,老师一定要注重数形结合的思想的应用,引导学生在课堂上对相关问题进行主动探究,培养学生的数学创新能力,提高学生的解题速度,丰富学生的解题思路,从而有效的落实新课程改革当中培养学生学科核心素养的要求。
一、采用数形结合思想对培养初中学生数学核心素养的意义
初中阶段的数学课程内容在慢慢的由直观化向抽象化进行转变,随之数学内容的难度也会逐渐增加。这就意味着初中生在学习数学的过程当中,将会面临更多的挑战。所以在数学教学过程当中,老师可以将数形进行有效的结合,把抽象的数学问题通过图形直观的表示出来,让学生的思维更加形象化,提高学生对数学知识的理解程度,这对培养学生数学核心素养具有非常积极的意义。在初中数学教学过程当中可以通过以下几个方面来进行数学思想的应用。其一,可以将相关的数学内容通过代数建模直观的表现出来,像初中数学里面涉及到的方程、不等式、函数等数学知识,都可以利用相关的代数建模,让学生对数学知识进行直观的认知和理解。其二,对于初中数学里面涉及到函数、不等式等知识,可以利用几何建模直观的反映问题。其三,老师在教学过程当中可以充分运用数形结合的思想,尤其是在学习函数和几何知识相关内容的时候,可以通过数学建模,直观展现教学内容,促进学生对数学知识进行高效理解和吸收,进而让学生学会运用一定的数形结合思想去解决数学问题,培养学生灵活运用数学知识的能力以及解决实际问题的能力,为学生数学核心素养的形成奠定良好的基础。
二、在初中数学思想教学过程当中,对数形结合思想的具体应用
(一)在初中数学有理数教学内容当中对数形结合思想的应用
在初中数学教学过程当中,数轴知识的学习为数形结合思想的应用奠定了良好的基础,也有效的解决了学生对有理数学习的难度。因为每一个有理数都可以在数轴上找出它唯一的对应的那个点,所以对两个已知有理数进行大小对比的时候,就可以采用数轴的方法,将两个有理数的具体位置在数轴上标注出来,其大小对比结果一目了然。同时在学习相反数和绝对值相关数学知识的时候也可以利用数轴,以原点为对称点,然后来描述具体的绝对值和相反数的位置。并且在后期学习实数的过程当中,也可以利用数轴对实数的大小进行直观比较。所以在数学教学过程当中,老师对这几个部分教学内容学习的时候,都可以给学生教授相应的数形结合方法,也就是将有理数和数轴进行紧密结合,引导学生通过建立数轴,对有理数、绝对值、相反数以及实数的内容进行一定的了解和运用。
比如在进行“有理数”学习的时候,教学时以生活当中常见的温度计来提出数轴,它通过数轴将数与形集于一体,以平面图像的形式,进行负数的学习,例如如下图所示:+2与-2,+4与-4,+6与-6,它们都是以距离原点0距离相等位置分布在数轴的两边,可以更加形象的看出负数的意义,呈现出来的数量关系非常的直观。
(二)在初中数学方程教学内容当中对数形结合思想的有效应用
方程作为初中数学教学当中的重点内容,它往往是以代数的形式呈现在学生的面前,但是仅仅采用代数的方法来解决方程相关问题,有时候显得过于繁琐,加大了解方程的难度,而在解方程的过程当中采用图形结合的思想,可以将方程演变成函数,然后做出一定的函数图像,进而简单直观的解决相关问题。
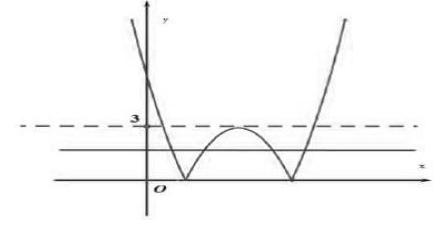
例如,已知方程|a2-6a+6|=b方程有4个根,求b的取值范围。
由题目当中可知,已知方程有4个根,那我们在解题的时候可以将其利用图形结合的思想将其转化成函数图像的交点问题。去掉已知方程的绝对值,令y=a2-6a+6得出y=(a-3)2-3将a看成x,坐标轴上画出函数的图像,然后将函数y以x轴为对称轴向上翻折就可以得到已知函数y=
|a2-6a+6|的图像,然后,我们再令y=b,再做出y=b的函数图像,这时我们观察两个函数图像,很容易发现函数图像上两个图像的4个交点就是已知方程的4个根,当然b的取值范围为(0,3)也就显而易见了,问题就很容易得到解答了。
如果在解决上述问题的时候,不利用图像进行直观表示的话,通过一定的运算来得出相应的结果,那是相当复杂而且具有一定难度的。但是如果转换思路,将题目当中的方程以函数的形式利用相关的图像表现出来,就可以很容易的得出问题的答案,这不仅大大降低了问题的难度,而且提高了学生的解题效率。
(三)在初中数学教学过程当中,采用数学结合思想培养学生的数学核心素养
通过以上数形结合思想在有理数和函数当中的具体应用,我们就可以看出,通过数形结合的思想可以将数学问题当中比较难以理解和难以计算的参数直观的表现在图像上,并且清楚的反映出相关数学参数与图像之间的关系,进而很快的得出问题的答案。学生在利用相关数学问题与图像建立关系的过程当中,他们的思维得到了一定的拓展,而且学会了如何将数学抽象的理论知识进行一定的化简,从而利用简单的图像法来探究问题、解决问题,培养学生的探究能力和创新能力。并且利用数形结合的方法解决数学问题让学生的思维更加活跃,不仅提高了学生的解决问题的效率,而且也让学生对数学本质的意义进行更深层次的理解,从而促进学生数学核心素养的培养。
比如在学习初中数学勾股定理相关知识的时候,一般老师首先都会引用公式a2+b2=c2,如果采用代数的理念来对勾股定理进行一定的理解,那是具有一定难度的,而且也是没有办法推导出a2+b2=c2的。所以这个时候就可以将三角形引入其中,将a,b,c导入图形当中,并且将三角形放在正方形当中进行不断的变换,让学生去观察变化后图形的相关规律和特点,进而引导学生对公式进行推导。对于数学当中的相关定理的推导,一般都要借助图形来进行公式的推导过程,这样才能够让学生更深层次的理解其数学定理的来源,也大大提高了学生对数学定理的应用能力。
三、如何将数形结合思想有效的切入到初中数学核心素养的培养当中
(一)对教学方式进行一定的优化和创新
在初中数学教学過程当中,采用有效的数形结合思想,可以持续性的培养学生的数学核心素养。不过在教学过程当中,老师也要注重教学方法的应用。目前在新课改的背景下,很多老师都摒弃了题海战术的传统教学方法,但是题海战术在一定的教学情况下还是有明显的效果的,它可以帮助学生提高解题速度。目前老师在对学生进行相关习题训练的时候,可以将科学的数形结合思想与传统的教学方式进行有效的融合,从而提升学生在数学方面的综合能力。
比如在学习圆的相关知识的时候,因为这个章节里面涉及的内容比较多,所以老师为了提高教学效率,一般都会采用数形结合的方式来将圆与直线的关系进行一定的展示,让学生更加透彻的明白,圆与直线的相交、相离、相切这三种关系,这样不仅加深了学生对有关于“圆”知识概念的理解,而且也为后面有关于圆的计算奠定了良好的基础。
(二)在数学教学过程当中要不断拓展学生的思维
学生在初中数学教学过程当中,对数学知识的不断积累,也代表着学生解决数学问题的能力也在不断的进行提升,当然数形结合思想在学生数学能力提升的过程当中发挥着至关重要的作用。所以在数学教学过程当中,老师要不断的强化学生的数形结合能力。在课堂上以学生为主体,跟学生进行积极主动的互动交流,引导学生对数学当中存在的问题进行分析和研究,并且在关键时候给予有效的指导,引导学生利用数形结合的方法寻找解题的思路和出口,从而改变学生在解决数学问题当中的定向思维,让他们的思维得到一定的拓展,进而提高学生解决问题的能力。
比如在学习“数据的收集,整理与描述”的相关数学知识的时候,它需要学生对相关事件进行普查和抽样调查,但是里面涉及的相关数据比较繁杂,单单靠代数知识是没有办法进行直观展示的,所以这个时候就可以利用统计图和统计表来将相关数据进行有效的整理,根据统计图和统计表里面反映的情况,进行相应的代数计算,这样就可以大大简化了代数方面的繁琐数据,直观的将调查结果展示出来,不仅让学生掌握了统计学方面的知识,也让学生学会了利用数学知识解决生活实际问题。这对培养学生数学核心素养具有非常大的促进作用。
四、结束语
总而言之,数形结合思想作为初中数学教学过程当中的主要思想,它能够帮助学生理解数学当中很多比较抽象的概念,简化数学当中比较复杂的题目,丰富学生的解题思路,提高学生的解题效率。所以在教学过程当中,老师一定要注重学生数形结合的思想的运用,在课堂上利用直观的图形将数学的实质展示出来,让学生对相关数学概念进行深层次理解和掌握,从而培养学生的学习兴趣,并且在课堂上不断的引导学生进行实践操作,学会利用代数知识解决图形问题,利用相关图形解决代数问题,并且将代数知识与图形进行有效结合解决数学问题,拓展学生的解题思路,促进学生发散思维能力的提升,从而帮助学生培养良好的数学核心素养。
【参考文献】
[1]马双平.数形结合在初中数学教学中的运用分析[J].科技资讯,2020,18(11):155-156.
[2]余云洲.相互渗透,交叉作用——初中数学教学中数形结合思想的应用探析[J].教育现代化,2019,6(06):114-
115+170.
[3]许婷婷.行走在数学核心素养下数形结合理念的创新之路——以《加法交换律和结合律》为依托的教学课例研究[J].华夏教师,2018(21):29-30.
