基于变异系数和最大特征树的特征选择方法

徐海峰,张 雁,刘 江,吕丹桔

(西南林业大学大数据与智能工程学院,云南 昆明 650224)

特征选择一直以来是机器学习和模式识别等领域的热点研究问题[1-2]. 它是数据预处理的必需过程,其目的是在特征空间中挑选出冗余度低、判别性高的特征子集[3],从而避免“维数灾难”的发生,它将直接影响数据分析的时间成本、模型的泛化性和解决目标问题的效果及性能[4].

特征选择可分为两部分:特征贡献度评分和特征优选. 特征贡献度评分是特征选择的关键过程,为了度量数据特征之间的相似性和差异性,按照指定度量规则计算特征对分类空间的贡献度. 从方法而言,可分为4类:基于相似度、基于信息论、基于统计方法和基于稀疏学习[5]. 目前,已经有大量研究提出许多不同的特征评分算法[6],包括在无监督特征选择中利用Laplacian算子评估特征贡献度[7]、在环境音识别中使用Constraint Score进行特征评分[8]、在利用SVM诊断心脏病中使用Fisher Score筛选特征[9]和基于变异系数对遥感数据进行降维[10]等. 特征优选则是从特征评分序列中挑选出冗余低、易分类的特征子集,该过程可分为封装式、嵌入式和过滤式3大类. 近年来不少研究基于这3种方式提出了很多优化算法,如使用二进制蜻蜓优化的特征选择[11]、基于粒子群算法的特征优选[12]、基于人工蜂群和梯度提升决策树的特征选择[13]和基于人工蚁群的特征选择[14]等. 文献[11]的方法是将连续特征搜索空间映射到离散空间,并提出S变形和V变形作为蜻蜓优化算法的传递函数进行特征优选;文献[12]将互信息作为特征贡献度评价指标结合粒子群算法剔除冗余特征;文献[13]使用文献[14]中提出的梯度增强决策树作为特征贡献度评价的方法,再利用人工蜂群对评价后的特征子集进行特征优选. 文献[15]以Pearson相关系数对特征评分,使用人工蚁群对特征进行优选.

目前,计算特征贡献度的方法都是基于空间距离度量特征之间的相关性和差异性,如Constraint Score和Laplacian,虽然算法复杂度低,但忽略了特征之间量纲不一致的问题,而且由于数据样本类内离散度不一致,随机抽样对结果也会产生影响;另外一些算法从概率统计学角度,用互信息对特征进行评分,例如文献[12]计算每一个特征样本与分类标签的互信息,虽然解决了量纲不同的问题,但是忽略了类内差异. 此外,分类标签为离散数据,特征样本有离散数据也有连续的,未经处理直接计算某特征和标签列的互信息是不合理的. 近年来,许多研究将特征优选过程看作优化过程[6],并结合许多智能算法搜索目标特征,但是对于数据量较大的数据集,多目标优化算法时间、空间复杂度比较高,而且利用多目标优化算法降维增加了模型的敏感性,降低其泛化性.

针对上述问题,本文从最小化类内距离和最大化类间距离的角度出发,利用变异系数和互信息的特点,提出CVMI(coefficient of variation and mutual of information)特征贡献度评分方法,将其融入嵌入式特征优选中,不仅能解决量纲不同的问题,而且能有效减少特征,提高建模精度;此外,本文还提出了一种基于CVMI特征评分结合最大生成树和二邻域去冗余的特征优选CVMI-RRMFT(remove redundancy of maximum feature tree)方法,该方法不仅能剔除冗余特征,有效降低算法的复杂度,而且能提高模型的精度和泛化性.

1 CVMI特征评价

在分类问题中,分类结果的好坏取决于选定特征的可分性. 特征优选原则:类内距离小、类间差异大. 本文提出一种联合类内变异系数CVAC(coefficient of variation for intraclass)和类间互信息MIIC(mutual of information for interclass),构建联合指标CVMI(coefficient of variation and mutual of information)来评价特征贡献度,结合嵌入式方法进行特征选择.

图1 CVMI特征选择方法Fig.1 The method of CVMI feature selection

基于CVMI的特征选择过程如图1所示,步骤如下:

Step 1:对原始特征使用CVMI方法对其评分,升序排序记作F,初始化特征子集F′=∅;

Step 2:从F中正向选择一个特征,纳入F′中;

Step 3:将F′映射至训练集Tr(Train Dataset)和测试集Te(Test Dataset),得映射集合Tr′、Te′;

Step 4:使用分类器对Tr′、Te′建模和分类评价,将评价指标k(准确率或Kappa等)记录到K中;

Step 5:重复Step 2至Step 4过程,直到F′包含F中所有元素;

Step 6:找到K中最大值对应的特征个数m,将F中的前m个特征作为最终特征子集.

1.1 类内变异系数CVAC

在统计学中,变异系数是用来度量两个或多个观测值样本的变异程度,也可以用于测量它们之间的离散度. 其表达式如下:

Cv=σ/μ.

(1)

式中,μ、σ分别为样本的均值和方差. 在特征空间为F,分类空间为C的问题中,特征f(f∈F)的类内变异系数为:

(2)

式中,Cvi为第f个特征中第i类样本的变异系数,CVACf表示C中第f个特征的类内变异系数. 当CVACf越大,则第f个特征的离散度越高,反之,则第f个特征较为内聚.

1.2 类间互信息MIIC

在信息论中,互信息用于度量两个变量的依赖或相关程度. 对于两个随机离散变量X和Y,互信息I(X;Y)的计算表达式为:

(3)

式中,p(x,y)表示x和y的联合概率分布函数,p(x)和p(y)表示x和y的边缘概率密度.I(X;Y)的取值区间为[0,1],I(X;Y)等于0时说明两个变量相互独立;I(X;Y)越大,则X和Y联系越紧密.

通常而言,用互信息评价属性贡献度时,X和Y分别为某特征向量和标签向量[12,16],但是特征向量和标签向量数据类型存在不一致:特征向量多为连续数据,而标签向量多为离散数据. 本文用互信息度量类间距离,X和Y表示为同一特征下不同类的样本向量. 若分类空间和特征空间同CVAC,则第f个特征的类间互信息MIICf如下:

(4)

式中,i,j(i≠j)分别为第f个特征中第i类和第j类的样本,MIICf为F中第f个特征的类间互信息.MIICf越小,则第f个特征类间差异越大,反之亦然.

1.3 协同指标CVMI

根据属性评价原则:类间差异大,类内距离小. 本文提出CVMI用于评价特征贡献度,计算表达式为:

CVMIf=λCVACf+(1-λ)MIICf.

(5)

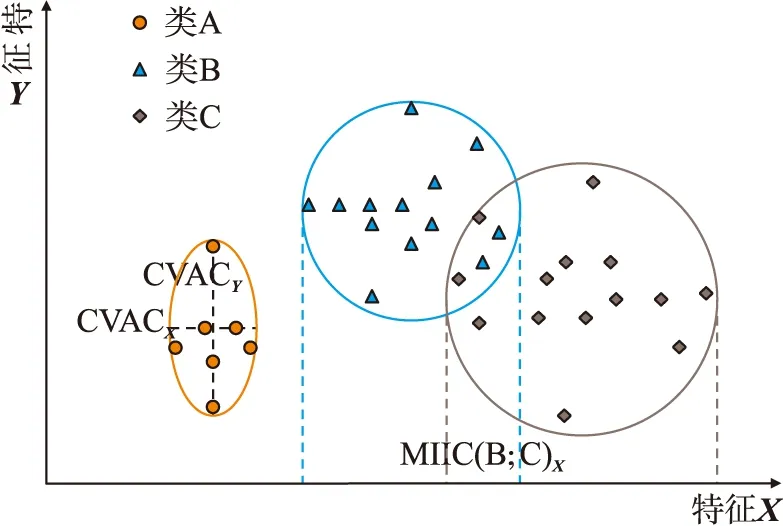
图2 CVMI示意图Fig.2 The schematic of CVMI

式中,对于特征优选,CVACf、MIICf都要小. 考虑到度量类内和类间指标权重不一致,引入调节参数λ,平衡二者的权重.

如图2,在分类空间C={A,B,C}的样本空间中,A类样本的特征X与Y的类内距离为CVACX、CVACY. 显然,CVACY相对CVACX较离散;在特征X中,B类样本和C类样本的类间距离为MIIC(B;C)X,即B类和C类映射在特征X上的互信息;如果随机变量相互独立,则互信息为0,如图2中A类样本与B类样本在特征X上的映射交集为∅. 由此可见特征X下样本可分性较高.

2 CVMI-RRMFT

除对特征进行贡献度评分外,还要考虑特征之间的相关性. 本文基于特征评分与去冗余提出CVMI-RRMFT(remove redundancy of maximum feature tree)的方法,利用CVMI贡献度评分序列构建最大特征树,再根据RRMFT方法剔除冗余特征.

图3 CVMI-RRMFT流程图Fig.3 The flow diagram of CVMI-RRMFT

该方法属于过滤式特征选择,流程如图3所示. 计算原始特征集相关系数邻接矩阵,构建最大特征树T;同时对每个特征使用CVMI算法得到贡献度评分序列F. 联合T、F根据二邻域方法剔除冗余特征,确定特征子集.

2.1 构建最大特征树

最大特征树,根据最小生成树衍生而来. 在无向图G(V,E)中,每边都有一个权值w,最小生成树则是在G中选取一个边集合E′,使得在V中所有点都被E′所连接,同时让E′中所有边权值之和最小. 最大特征树中的节点V为特征属性,使得E′中所有边权值之和最大,边权值由Pearson相关系数决定.P(Fr,Fc)表示特征Fr和Fc的相关性,其计算表达式:

(6)

(7)

式(6)中Fri表示第r个特征的第i个样本点,Fr表示第r个特征样本的均值. 式(7)中I(Fr,Fc)表示属性Fr、Fc的带权相关度. 由式(6)、(7)计算出相关系数邻接矩阵,构建最大特征树,算法MaxFT(Maximum Feature Tree)描述如算法1.

算法1构建最大特征树MaxFT

算法名称:构建最大特征树MaxFT

输入:相关度矩阵Dn×n;(n为特征个数)

过程:(1)初始化无向图G={1}

(2)while |G| ≤ndo

(3)c=nG

(4)m=D的{G×{c} }子矩阵中最大值列标

(5)G=G∪m

(6)end while

(7)returnG

输出:最大特征树G

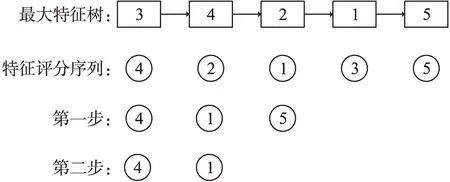
图4 二邻域剔除冗余特征Fig.4 Remove the redundant features with two-neighborhood

2.2 二邻域剔除冗余

根据最大特征树,结合CVMI特征贡献度评分方法计算得出评分序列(按照评分方法指定规则进行排序),剔除冗余特征,操作步骤如图4所示.

示例:如图4,CVMI特征评分序列F={f4,f2,f1,f3,f5},遍历F,如第一个特征x=f4.

Step 1:在最大特征图中寻找x所在位置,得出相邻元素m={f3,f2},在F中将m删除,得出F′={f4,f1,f5};

Step 2:依次遍历F′中未遍历的元素,取x=1,同理可得m={f2,f5},在F′中将m删除,F′={f4,f1};

Step 3:F′={f4,f1}该集合元素已经全部遍历,则最终特征序列为{f4,f1}.

3 实验

3.1 实验准备

表1 数据集信息Table 1 Data set information

(1)实验数据

本实验选用6组数据集,其中4组数据集为UCI[17]提供:Sonar,Vehicle,Diabetes和Ionosphere;另外2组数据为遥感数据RS和鸟鸣数据Birds. 每组数据按7∶3的比例划分训练集和测试集. 数据集信息如表1所示.

(2)实验设置

在实验中,为验证CVMI和CVMI-RRMFT方法的有效性,将它们与Constraint得分(CS)[8]和Weka平台提供的6种特征选择方法:Correlation(Cor)、GainRatio(GR)、InfoGain(IG)、OneR(OR)、ReliefF(RF)、SymmetricalUncert(SU)作对比. 并设置CVMI计算式中的λ值为0.8.

(3)分类器与性能评价

本实验以决策树为分类器,对特征贡献度评分序列F(每种评分方法按照指定规则排序,如CVMI为升序)正向选择,映射训练集和测试集,评价指标使用Kappa系数,其表达为:

(8)

式中,po为总体分类精度(Acc),即所有正确样本个数m除于样本总数n,如式(9):

po=m/n.

(9)

pe基于混淆矩阵计算而来:假定每一类真实样本个数为a1,a2,…,an,每一类预测样本为b1,b2,…,bn,则有

(10)

在本实验中每组数据独立重复运行10次,并计算10次的Kappa系数的均值.

图5 CVMI正向特征选择评估Fig.5 CVMI method forward feature selection evaluation

3.2 CVMI实验结果与分析

在图5中,CVMI方法为带*号标记的线条. 从Kappa峰值可以看出CVMI方法能有效提高建模精度:CVMI方法Kappa峰值相比其他7种方法可达最高,在Sonar、Vehicle和Diabetes数据上,分别提高2.65%、3.10%和1%;在Ionosphere和RS数据集上,CVMI较其他方法而言使用特征数最少就能达到精度峰值,图5(f)效果更为显著,由该图可看出本文CVMI方法均比其他7种选取很少特征就能达到Kappa峰值,符合特征优选和贡献度排序准则;其次,特征优选:计算特征贡献度排序后,根据该序列正向选择特征并进行分类测试,分类精度原则上应先是上升趋势,在达到峰值后,由于纳入的特征对模型可能存在一定干扰,则开始呈现波动趋势. 在图5中从Kappa曲线趋势来看:将Kappa峰值作为截止项,CVMI较上升趋势较为稳定,而其他7种方法波动幅度大.

在表2中,CVMI方法除在Diabetes数据集上性能不明显,在其他数据集上均是使用最少的特征数Kappa值就能达到最高值,尤其在60维的Sonar数据和33维的Ionosphere数据上效果显著. 在Sonar数据集上,7种对比方法中SymmetricalUncert使用特征数最少为28个特征,而其他6种方法均为50个特征以上,但SymmetricalUncert对应Kappa值为0.81,而CVMI仅用21个特征Kappa值就达到0.87,对比 SymmetricalUncert 方法增长了6%;在遥感数据集RS上GainRatio方法使用特征数最少,使用7个特征计算Kappa值为0.63,对于CVMI虽然用了8个特征,但Kappa值对比GainRatio方法提高了3%;表现效果最佳的是Birds数据集,仅用了9个特征达到了Kappa峰值,对比其他7种方法,降维率为75%. 对于RS数据集ReliefF方法精度和本文方法相同,但ReliefF使用了20个特征,CVMI仅使用8个特征. 同时还对原始数据进行实验对比,可以看出,CVMI不仅能有效地降低维度,而且还有效提高了建模精度.

表2 不同数据集使用不同特征贡献度评价方法对比结果Table 2 Comparison results of different data sets with different feature contribution evaluation methods

3.3 CVMI-RRMFT实验结果与分析

在CVMI-RRMFT选择特征方法实验中,使用3.1中Weka 6种特征评价方法:Cor、GR、IG、OR、RF、SU和CS[8]方法以及本文方法CVMI,计算特征贡献度评分序列,将该序列结合去冗余方法RRMFT;分类器采用决策树J48,对选定的特征子集在训练集和测试集上映射. 每组实验独立重复10次,并计算10次准确率的均值.

实验结果如图6,横坐标表示7种特征评价方法和本文CVMI方法,ORI为原始数据;纵坐标表示10次准确率的均值;柱状图正上方对应的数字为选定的特征个数. 图6中,RRMFT(采用8种不同特征贡献度评分)方法对比原始数据,6组数据都表明RRMFT不仅能有效地降低维度,而且有效提高了分类准确率.

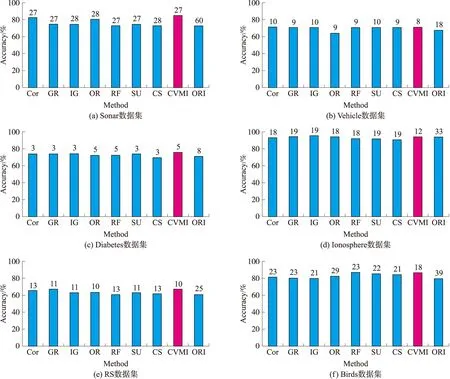
图6 不同数据集的RRMFT特征选择性能Fig.6 Accuracy of RRMFT feature selection with different data sets

在表3中,对6组数据而言,8种特征评分方法结合RRMFT都将维度降低至50%到55%,在Sonar、Vehicle、RS和Birds数据集上,都是使用最少的特征数达到最高的准确率;本文CVMI-RRMFT方法Sonar的降维率为55%,准确率较原始数据提高12%,Birds降维率为53.85%,准确率较原始数据提高9.71%;在Ionosphere数据集上准确率InfoGain最高,本文CVMI方法与其相差1.13%,但降维率是最高的. 综上所述,CVMI-RRMFT在降维和提高模型准确率上效果显著.

此外,本文还对CVMI和CVMI-RRMFT两种特征选择方法进行了实验对比. 在实验中,使用CVMI和CVMI-RRMFT方法进行特征选择后,将Kappa和准确率(Acc)作为评价指标. 如表4所示,6组数据集 CVMI-RRMFT方法准确率都高于CVMI方法,其中Sonar数据集的效果最为显著:Acc高出4.35%,Kappa高出0.04;在数据RS中CVMI和CVMI-RRMFT的表现一致;在Vehicle数据集中Acc指标相同,CVMI 的Kappa系数对比CVMI-RRMFT仅高出0.01. 综上所述,CVMI-RRMFT方法对比单独使用CVMI性能更强.

表4 不同数据集使用CVMI和CVMI-RRMFT方法的实验结果Table 4 Experimental results of CVMI and CVMI-RRMFT methods used in different data sets

4 结论

大数据时代,降维是不可或缺的步骤. 对此,许多研究将特征评价和去冗余作为多目标,从而提出不同的优化算法,但是对于海量数据而言,时间成本是非常高的. 另外,在特征相关性分析时数据存在不同量纲. 本文提出了嵌入式CVMI特征选择方法,使用变异系数和互信息度量类内和类间距离,解决了属性量纲不同的问题,能有效选择较优的特征提高分类精度,而且对比其他特征评选方法,更符合特征评选的客观趋势;此外,将CVMI与去冗余方法RRMFT结合,综合考虑特征贡献度和特征相关性,通过实验证明该方法能有效遴选出可分性高、冗余度低的特征. 实验使用了UCI提供的4组公共数据集和两组自建数据,本文方法在这些数据集上表现都是良好的,更好地结合特征评价和冗余去除也是未来的研究方向.