基于金属化过孔的三维频率选择表面研究

杨 霞,于正永,陆华丽,唐万春

(1.南京师范大学物理科学与技术学院,江苏 南京 210023)(2.江苏省先进通信声频技术工程实验室,江苏 南京 210023)(3.江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023)

频率选择表面(frequency selective surface,FSS)是由具有特定形状的相同单元结构周期性排列而成的无限大二维阵列结构,不同形状的周期单元具有不同的空间滤波特性[1]. 在卫星通信应用中,具有小通带比、高选择性、小单元尺寸、双极化和较好的角度稳定性的双频FSS备受关注[2].

近年来,很多研究人员采用传统二维结构提出一些相关性能的FSSs:(1)通过级联两个相同的周期性阵列,实现具有多个传输极点和零点的小通带比的双频FSS[3]. (2)利用加载集总元件来实现小通带比、小型化的双频FSSs[4-5]. (3)基片集成波导(substrate integrated waveguide,SIW)技术首先用于设计的FSS表现出较高的频率选择带通响应[6]. 后来,研究者采用SIW技术实现了双环槽的双频FSS[7]. (4)通过利用横杆分形结构实现了一个双极化三频带FSS[8]. 但由于传统的二维FSS结构存在谐振方式有限、频率选择性能一般、难以实现多传输零极点等缺点,越来越难以满足现代微波与通信系统对FSS的性能需求[9]. 随着对FSS进行深入研究,近年来一种新颖的三维频率选择表面(3-D FSS)概念被提出,能够在一定程度上解决传统FSS存在的局限性[10],相比于传统的2-D FSS多了一个维度的设计自由,3-D FSS能够借助三个设计维度来构造谐振器,因此可较为容易地在一个单元内产生多个谐振实现良好的滤波性能[11-12]. 然而,大部分3-D FSS几何结构比较复杂,本文提出了一个结构简单、高性能的3-D FSS.

本文提出了一种结合传统滤波器的双模谐振理论的双频3-D FSS. 该结构通过在平行板路径中加载金属化过孔来构建双模谐振器,将原有的单个谐振模式分裂为奇模和偶模两种谐振模式[13-14],从而产生两个传输极点. 由于不同传输路径中电磁波相位反相,在两个通带外各引入了一个传输零点. 通过适当的设计参数,得到了一种具有高频率选择性、小通带比的双频FSS. 通过分析传输零极点处的电场分布,阐明了所提出FSS的工作机理. 从仿真结果可知,所提出的3-D FSS具有高频率选择性、小通带比、双极化、较好的角度稳定性等优势.

1 加载金属化过孔的双模谐振器

加载金属化过孔的3-D FSS的周期单元结构示意图如图1所示. 由图1可以看出,该FSS的周期大小为p,高度为h,方形金属管的边长为a,介质的相对介电常数为εr. 该FSS的每个周期单元均以平行板路径为电磁波传播路径. 平行板路径由相邻的外方形金属管和介质组成,且在平行板路径的中心位置加载了4个直径为d的金属化过孔,使得周期单元形成两个上下一样的谐振单元.

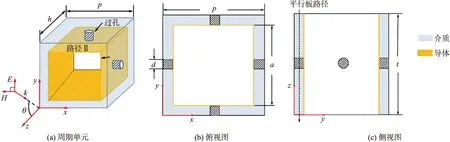
图1 加载金属化过孔的3-D FSS的周期单元结构Fig.1 The periodic unit of 3-D FSS with metallized vias

图2给出了TE波垂直入射条件下该3-D FSS的反射系数和传输系数HFSS软件仿真结果,基本参数见表1.

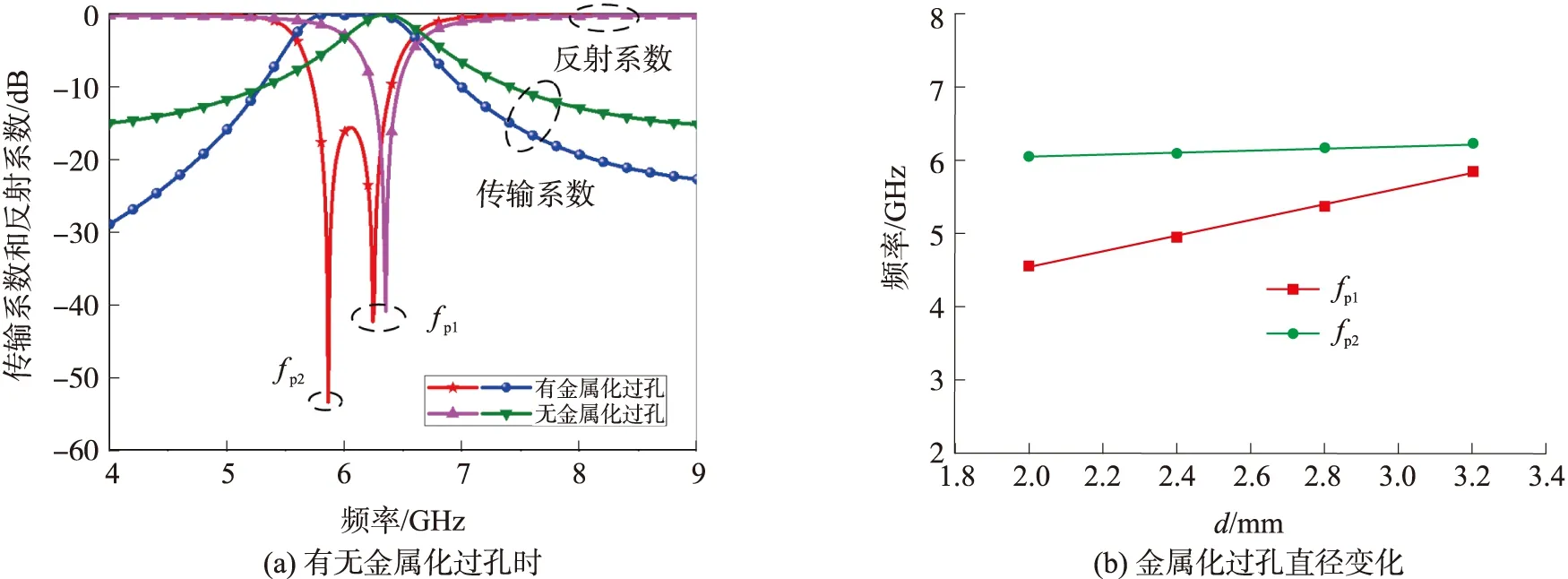
图2 金属化过孔对传输极点的影响Fig.2 Effect of metallized vias on the transmission poles

表1 所提出3-D FSS结构参数Table 1 Parameters of the proposed 3-D FSS mm

由图2(a)可以发现:该结构增加金属化过孔后,会在原有传输极点fp1的低频侧又增加一个传输极点fp2,从而获得了一个平坦的通带. 图2(b)给出了传输极点fp1和fp2的谐振频率与金属化过孔直径d的关系曲线,可以看出在其他参数不变的情况下,当金属化过孔的直径d增加时,传输极点fp1的谐振频率呈现明显递增趋势,而传输极点fp2的谐振频率则基本保持不变,这是金属化过孔半径增大使得其电感值随之减小形成的. 进一步说明了金属化过孔的直径d仅与传输极点fp2的谐振模式相关.

为了理解该双模谐振器的工作机理,对谐振器工作在传输极点处的电场分布进行了分析,如图3所示. 图3(a)给出了传输极点fp1处的电场分布,在该频率下当电磁波入射到该FSS上时,平行板路径被主要激励. 这里假设以周期单元一半高度处为对称面,对称面两侧区域内的电场幅值在两端处具有最大值,在中心处的金属过孔处具有最小值,且对称面两侧的电场方向没有发生改变,根据奇偶模分析方法,可以得知该频率下对称面为理想磁壁,因此路径Ⅱ中的两个1/4波长短路谐振器通过中央缝隙发生容性耦合,通过偶模形式产生传输极点fp1. 在图3(b)中,在对称面两侧区域内的传输极点fp2处的电场幅值相同、方向相反,因此传输极点fp2是由奇模耦合状态下1/2波长谐振产生,该频率下对称面此时可以等效为理想电壁. 该结构是加载过金属化过孔来构成两个同样的谐振单元,从而形成了双模谐振器,在奇偶模耦合的作用下,分裂为两个传输极点来实现通带性能.

图3 谐振器工作在传输极点对应的电场分布图Fig.3 E-field distributions of the resonator at transmission poles

为了加深对该结构的理解,运用传输线电路来进行分析,如图4所示,在不考虑端口不连续性影响的情况下,该单元结构可以看作为两个相同的平行板传输线和等效电感的互连,因此可以得到对应的等效电路模型. 如图4(a)所示,加载的金属化过孔可以等效为一个电感[11],用电感元件Lr来表示. 同时,平行板传输线的特性阻抗和电长度分别用ZPPW和θ来表示,Z0为自由空间波阻抗Z0=377 Ω. 由于该等效电路模型关于参考面TT′对称,因此可以对该结构的电路用奇偶模分析方法,只需分析对称面处于理想电壁或理想磁壁条件下一半的电路结构即可. 如4(b)所示,在偶模状态下,参考面等效于一个理想磁壁,相当于对称线上各节点处于开路;如4(c)所示,在奇模状态下,参考面等效于一个理想电壁,相当于对称线上各节点处于短路. 由等效电路模型可以看出,偶模状态下的传输极点与金属化过孔等效电感Lr有关,而奇模状态下的传输极点与金属化过孔等效电感Lr则无关.

图4 加载金属化过孔的平行板路径等效电路分析Fig.4 Equivalent circuit analysis of 3-D FSS with metallized vias

由文献[15]可知,平行板传输线的特性阻抗和电长度计算公式可如下表示:

(1)

(2)

式中,角频率ω=2πf,μ0是自由空间磁导率,ε0是自由空间介电常数,εr是平行板路径填充介质时的相对介电常数.

从图4(b)可知,在偶模状态下平行板传输线的输入阻抗可定义为:

(3)

易知,所对应的偶模状态下的输入导纳Yeven=1/Zeven.

由文献[16]中的计算公式可以得到金属化过孔的等效电感Lr可定义为:

(4)

式中,l为金属化过孔的长度,即l=(l1-l2)/2;r则是金属化过孔的半径.

同理,在图4(c)中的奇模状态下平行板传输线的输入导纳可以定义为:

(5)

基于式(4)和(5)中的奇偶模输入导纳,可以获得该单元结构的散射参数,可由下面的方程组计算得到[17]:

(6)

(7)

2 加载金属化过孔的双频三维FSS

2.1 结构描述与性能仿真

基于以上分析,设计了一种加载金属化过孔的双频3-D FSS结构,其周期单元结构示意图如图5所示. 由图5可以看出,该FSS的每个周期单元包括方同轴线路径(路径Ⅰ)和平行板路径(路径Ⅱ). 方同轴线路径由内、外两个方形金属管和介质1组成,平行板路径由相邻的外方形金属管和介质2组成. 同时,在平行板路径的中心位置加载了4个直径为d的金属化过孔. 该FSS的周期大小为p,高度为h,两个方形金属管的边长分别为a和b. 介质1和2的相对介电常数分别为εr1=2.8和εr2=7.5.

图5 加载金属化过孔的双频3-D FSS的周期单元结构Fig.5 Dual-band 3-D FSS with metallized vias

图6 在TE波垂直入射时的S参数仿真结果Fig.6 Simulated Scattering Parameters of the proposed 3-D FSS prototype(TE polarization,normal incidence)

图6给出了TE波垂直入射条件下该3-D FSS的反射系数和传输系数HFSS软件仿真结果,基本参数见表2. 由图2可以发现:该结构产生了两个通带,其中低频通带有一个传输极点在fp1(5.46 GHz),高频通带包含两个传输极点fp2(7.1 GHz)和fp3(7.24 GHz). 这两个通带的中心频率分别为5.44 GHz和7.155 GHz,通带比为1.31,且3 dB相对带宽分别为 4.95%和 8.81%. 该FSS周期单元大小为0.164λ0×0.164λ0×0.145λ0,其中λ0为低频通带中心频率在真空中对应的波长. 此外,在带外引入了两个传输零点fz1(3.86 GHz)和fz2(4.55 GHz),使得通带的截止特性变得陡峭,有效地提高了频率选择性.

图7给出了该FSS在不同极化模式下和不同入射角度(0°,15°,30°和45°)下的传输与反射系数仿真结果,可以发现,该结构能够产生了两个陡峭通带及两个传输零点,并可以实现双极化性能,具有良好的角度稳定性.

表2 所提出3-D FSS结构参数Table 2 Parameters of the Proposed 3-D FSS mm

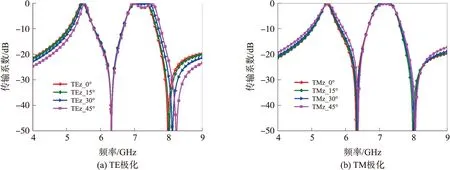
图7 不同角度入射波下传输系数Fig.7 Transmission coefficients under different incident angles

图8 基于方同轴线的双频3-D FSS的工作机理Fig.8 The working mechanism of the proposed 3-D FSS

2.2 原理分析

为了理解本文所提出的基于方同轴线的双频3-D FSS的工作机理,图8给出了此结构的工作原理示意图. 如图所示,入射电磁波从入射端的端口1进入,将平行板和方同轴两条路径激励起来,其中平行板路径具有两个谐振器R1和R2,分别在介质筒长度方向上产生1/4波长谐振(fp1)和半波长谐振(fp3),方同轴路径提供一个谐振器R3,在介质筒横截面上的一个波长谐振(fp2),于是传输系数具有3个传输极点,同时平行板路径中的谐振器R1、R2和方同轴路径中的谐振器R3具有相位反相,产生两个传输零点(fz1、fz2),最终经过FSS滤波后的电磁波将在端口2出射.

如图9所示,对本文所提出的双频3-D FSS的传输极点和零点处的电场分布进行了分析,来加深对该3-D FSS 结构工作机理的理解. 图9(a)给出了传输极点fp1处的电场分布,当电磁波入射到该FSS上时,可以得知该频率下对称面为理想磁壁,是由平行板路径的两个1/4波长谐振产生. 图9(b)为传输极点fp2处的电场分布,其主要分布在方同轴线路径中,从俯视图可知,在电磁波入射平面(xoy平面)内会产生方型槽谐振,该谐振波长大约等于介质筒的周长;从剖面图看,电场在z轴方向上具有相同的相位和幅度,故无谐振发生,因此可以得知传输极点fp2是由方同轴线路径的方型槽谐振产生. 在图9(c)中,传输极点fp3是由平行板路径的1/2波长谐振产生,该频率下对称面此时可以等效为理想电壁. 按照本文所述的双模谐振器的工作原理易知传输极点fp1和fp3是由平行板路径增加了金属化过孔而形成的,而传输极点fp2是由同轴路径的方槽谐振产生的,从而实现了多传输零极点性能.

图9 传输极点对应的电场分布图Fig.9 E-field distributions at transmission poles

如图10所示,在传输零点fz1和fz2的频率处,路径Ⅰ和路径Ⅱ同时被激励. 从图10(a)可以看出,当频率为fz1时,在两条传播路径末端处电场矢量具有180°相位反相,导致了电磁场相互抵消,从而产生了传输零点fz1. 同理,在图10(b)中,方同轴路径内发生了方型槽谐振和平行板路径发了生1/2波长谐振,在两条传播路径末端处电场矢量也具有180°相位反相,因此产生了传输零点fz2.

图10 传输零点对应的电场分布图Fig.10 E-field distributions at transmission zeros

3 结果与讨论

根据上述分析,易知该3-D FSS结构的传输零极点位置与周期单元的几何尺寸紧密相关,下面将结构的周期单元几何尺寸进行参数扫描,分析其对传输零极点的影响.

图11给出了该单元结构的不同参数尺寸,即不同的周期p、高度h、方形金属管外边长a和内边长b、以及金属化过孔的直径d对FSS结构性能的影响. 由仿真结果可知,在其他结构参数不变的前提下,当p增加时,带内传输极点fp1随之减小而低频右侧带外传输零点fz1随之增大,带内传输极点fp3随之减小,而传输极点fp2以及传输极点高频带外传输零点fz2均随之增大,如图11(a)所示. 当h增加时,带内传输极点fp1随之减小而低频右侧带外传输零点fz1基本保持不变,带内传输极点fp2随之增大,而传输极点fp3以及传输极点高频带外传输零点fz2均随之减小,如图11(b)所示. 当a增加时,带内传输极点fp1基本保持不变而低频右侧带外传输零点fz1随之减小,带内传输极点fp3随之增大,而传输极点fp2以及传输极点高频带外传输零点fz2均随之减小,如图11(c)所示. 当b增加时,带内传输极点fp1基本保持不变而低频右侧带外传输零点fz1随之减小,带内传输极点fp2随之减小,而传输极点fp3以及传输极点高频带外传输零点fz2均随之增大,如图11(d)所示. 当h增加时,带内传输极点fp1和低频带外传输零点fz1均随之增大,带内传输极点fp2随之减小,而传输极点fp3以及传输极点高频带外传输零点fz2均随之增大,如图11(e)所示.

图11 传输零极点随周期单元尺寸的变化Fig.11 Transmission zeros and poles varying with the size of the periodic element

根据以上的参数分析,下面给为能够快速设计出所需滤波特性的FSS提供了简单的设计指导,具体如下:

(1)当方形金属管的内边长b变化时,主要影响高频通带的带宽和带外的陡峭频率特性,当b增加时,低频通带基本不变,高频通带带宽变大,带外陡峭特性变差,因此可以通过调节该尺寸对高频通带进行优化.

(2)想要改善高频通带的带宽,改变高度h易于实现. 当参数h减小时,高频带宽变大,低频通带整体往高频移动,可通过调节该尺寸优化高频通带的带宽.

(3)改变金属化过孔的直径d可以使得两个通带整体往高频或者低频移动,易于满足对不同频段的需求.

4 结论

本文介绍了加载金属化过孔构建双模谐振器的工作原理,并在此基础上,提出了一种具有小通带比的双频3-D FSS. 通过在平行板路径加载金属化过孔,将原有单一的谐振模式分裂为奇模和偶模两种谐振模式,产生了两个传输极点,借助方同轴线的方型槽谐振产生第三个传输极点,同时不同路径之间的电磁波反相产生了两个传输零点,通过适当的设计参数,设计出了一种可以应用于卫星通信系统的高频率选择性、小通带比的双频FSS. 通过对所提出的FSS的传输零点和极点处的电场分布进行分析,详细阐述了所提出的FSS的工作原理. 仿真结果表明,所提出的3-D FSS在TE和TM极化、入射角度从0°到45°下具有稳定的频率响应.