考虑租赁双方的租赁设备多目标预防维护策略

刘勤明, 王雨婷, 叶春明, 李冠林

（上海理工大学 管理学院，上海 200093）

随着经济迅速发展，设备租赁行业逐渐兴起。由于设备租赁业务自身的特点，租赁设备维护策略的制定有别于传统设备。相较于传统企业自身拥有生产设备所有权，并对其进行维护管理、开展生产活动而言，生产设备租赁业务将设备的所有权与使用权分割，并将设备维护工作转移给出租方。因此，在租赁设备的维护策略制定方面，设备租赁双方经济利益的平衡与联合优化成为了国内外学者和企业研究的重点。

在现有研究中，租赁设备的维护方式主要分为两种：状态维护和预防性维护。例如：通过对设备内部衰退故障和外部冲击造成的故障加以区分，更加准确地优化维护周期[1]；结合准更新理论对周期性预防维护的维护周期进行优化以寻求更优维护成本，在两阶段维护的基础上，提出了多阶段预防性维护策略，将等周期和变周期维护策略进行结合[2]等。但是在实际生产中，预防性维护容易造成前期维护过剩、后期维护不足的问题，因此根据设备的当前状态决定是否对其进行维护，并确定采用何种维护方式更加贴近实际情况。例如：Chien 等[3]假定系统的劣化是遵循具有有限状态空间的非齐次连续时间马尔可夫过程，提出了一种递归方法，有效地计算多状态系统的最优维护调度。Shen 等[4]考虑了系统退化期间可能发生的多个突然故障，根据系统退化和不同故障模式的失效时间，建立了基于统计依赖性的维修时间的联合模型。除上述对出租方维护成本的考虑外，在租赁双方经济效益联合优化中，需同时考虑到承租方的生产需求。Mawson 等[5]以质量为导向的维护模型，建立了一种将过程变量与多维产品质量相连接的响应模型。在此基础上，方玲珍等[6]构建了基于比例故障率的设备开动率指标和基于响应模型的产品合格率指标，建立了多目标维护效率函数与设备预防维护模型。王华等[7]的研究从租赁企业视角出发，引入备件库存及备件运输等因素，建立租赁设备的等周期修复非新预防维护模型，通过最小化租赁维护和备件成本的总费用，获得租赁设备的优化维护策略，来指导租赁企业设备维护计划的制定及施行。金琳等[8]综合考虑了设备新旧程度、租金收入、故障惩罚等租赁设备特有因素，以虚拟年龄作为预防性维护修复程度的衡量标准，并使其随役龄增加，来抑制故障次数增加。其他学者也对租赁设备维护从不同角度进行了探讨[9-14]。然而，现有文献多从出租方角度进行考虑，忽略了承租方对租赁设备的使用要求，对承租方的满意度考虑不足。大多数研究都追求出租方经济利益最大化，往往忽略承租方的要求，忽略承租方的生产连续程度和满意程度等。

综上所述，本文首先根据租赁活动双方的实际需求，在设备的整个租赁期内，对设备进行故障检测，根据设备的故障状态对设备进行多维护方式的决策，包括预防维护、更换以及故障小修。利用承租方对生产产品的质量需求来描述其对租赁方的满意度，以最小化设备的维护总成本、总加工时间，最大化承租方满意度为目标建立多目标联合优化模型，优化租赁设备的预防性检测维护周期，最后通过仿真计算，得到租赁设备的最优检测周期和最优维护策略。

1 问题描述

以单个租赁设备为研究对象，在租赁期L内，由出租方对设备进行定周期检测维护，根据检测得到的设备状态选择相应的维护操作。每当设备到达检测节点时，对设备状态进行非破坏性检测，根据设备故障率h(T)所属的区间采取相应的维护策略。若h(T)＜ε1，则无需对其进行维护，故障率变化状态仍遵循前一周期的特征；若ε1≤h(T)＜ε2，则对其进行预防性维护（PM），对设备进行预防性维护后，设备状态恢复到0.5 周期前的状态，记故障率在PM 后恢复值为 Δh；若h(T)≥ε2，则对其进行更换，其故障率恢复到上一周期状态，即h1(t)=h1(t-T)。 其中： ε1和 ε2表示故障率阈值，且ε1＜ε2；T表示检测维护周期；t表示检测时间点。

租赁期内对含有m个工件的工件集J={j1,j2,j3,···,jm}进行连续加工，遇检测时间节点时根据设备状态决定其维护方式，确定是否对设备进行预防性维护或更换操作，同时也确定其停机时间，包括预防性维护停机时间和更换操作停机时间。根据维护策略的限制对工件集总的加工时长进行优化。

租赁设备的相关部件质量会对产品质量产生影响，随着相关部件质量的衰退，产品的质量特征偏差会逐渐增加，通过伽马过程对相关部件质量衰退的独立和非负增量的随机过程进行描述，利用租赁期内平均产品合格率来描述承租方的满意度。租赁设备发生故障时，实施小修修复，小修不改变租赁设备的损害情况，只维持租赁设备的正常运行。租赁设备预防维护操作可使设备回到全新状态。假设租赁设备进行预防性维护期间，设备状态不发生改变，设备停机阶段设备不会发生故障。

因此，从设备出租方角度来说，出租方需要优化设备总维护费用，包括预防性总的检测维护费用、生产周期内产生故障时的小修费用和租期结束后可能产生的租赁延迟费用。从设备承租方的角度来考虑，承租方需要最小化工件加工的总时长，即尽可能降低停机损失，同时保证产品质量，以此来提升承租方在租赁活动中的满意度。本文通过建立多目标预防维护模型，优化检测维护周期，提出最优维护策略，联合优化租赁双方经济效益。

2 联合优化租赁设备维护模型

2.1 租赁设备相关部件质量退化过程建模

设备中相关部件质量会对产品质量特征产生影响，从而影响产品的合格率，产品的合格率对设备承租方的生产经营活动至关重要。本文从相关部件质量对产品质量的影响出发，描述承租方的满意度。

影响产品质量的过程变量分为可调整过程变量和噪声变量。噪声变量通常随机变化，在正常条件下无法调整。可调整的过程变量是相关部件质量退化状态的度量，而相关部件质量的衰退过程通常是独立非负增量的随机过程。可调整过程变量记为X(t)=[X1(t),X2(t),···,Xs(t)]T，噪声变量记为Z=[Z1,Z2,···,Zl]T。

相关部件质量衰退的独立非负增量随机过程可以通过伽马过程来描述，则可调整过程变量Xs(t)的概率密度分布为

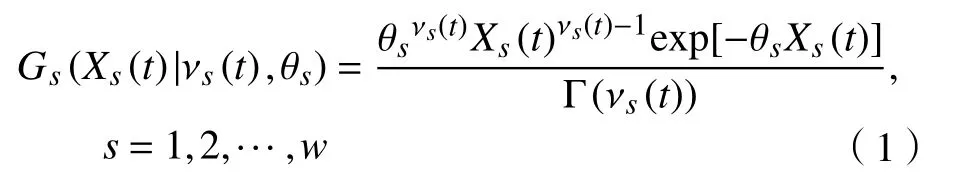
式中， νs(t)和 θs(t)分别为形状参数和尺度参数。

假定相关部件质量在租赁期开始时处于全新状态。相关部件质量的退化不仅会影响产品质量，同时也会对故障率产生显著影响。由于设备部件之间的相互作用，相关部件质量的衰退对设备的可靠性也存在影响。Weibull 分布是广泛应用于可靠性中的连续型分布，主要用于描述疲劳失效、轴承失效等寿命分布，则设备的故障率为

式中： α 和 η分别为Weibull 分布的形状参数和尺度参数； βm为 回归参数，表示Xm(t)对设备故障率的影响， β ∈Ri，Ri为工件加工结束时是否进行更换操作的决策变量。

由于相关部件质量衰退的不确定性，X(t)是随机的，则设备故障率函数是通过对X(t)求期望值得到的，即

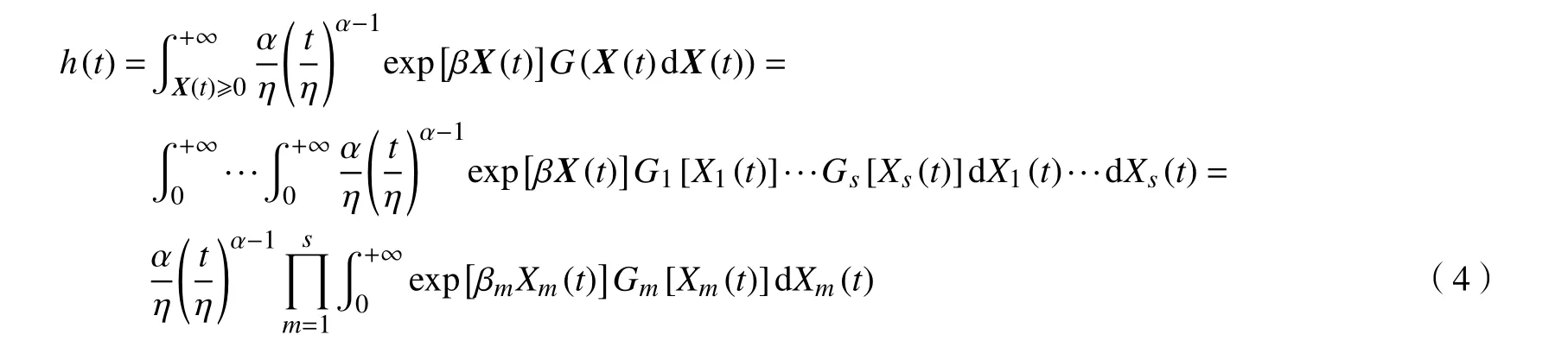
将式（1）代入式（4），则

式中，θm-βm>0,m=1,2,3,···

2.2 出租方总维护费用模型

首先从出租方维护费用优化的角度建立出租方总维护费用模型。在检测维护周期kT（k=1,2,3,···,N）内，对设备的故障率进行检测，则每个检测周期的维护成本由设备在当前检测周期的故障率h(kT)所 属的区间决定，则第k个检测周期的维护成本Ck可表示为

式中：Cp和Cr分别表示单次预防性维护成本和单次预防性更换成本；T为检测维护周期；N表示租赁期内设备进行检测维护的次数。

租赁期中设备总的预防检测维护费用CCk为

每个周期进行检测后，执行相应的维护策略，则其下一个周期的故障率变化为

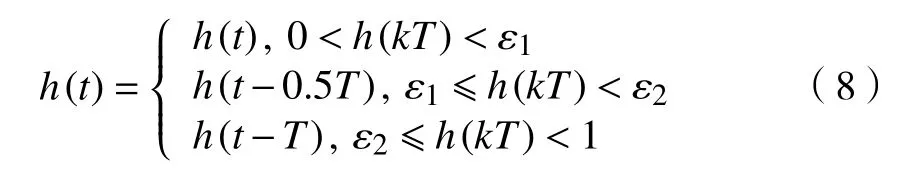
在租赁期内，如果设备产生故障，则对其进行小修，小修后设备恢复至故障前状态。租赁期内总的小修费用CCm为

式中：Cm表示单次故障小修成本；E[N(L)]表示租赁期小修停机次数，可表示为

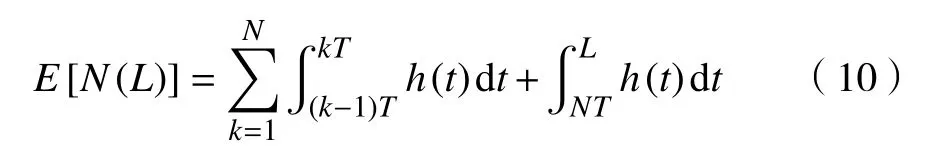
在设备租期结束后，出租方面临着寻找下一家租赁方的问题，在此期间，设备将会被闲置，即产生租赁延迟。若租赁期结束时，承租方直接与出租方续租，则不会产生租赁延迟成本；若租期结束时，设备故障率较高，承租方不愿意续租，则出租方需要承担一定的租赁延迟成本。租赁设备在休眠期同样会发生故障，但其故障率比运行状态下低。当设备处于休眠期时，假定其故障率函数为

式中， μ为故障率控制参数。

租赁结束时，设备故障率小于等于续租阈值γ时，承租方愿意续租；超过 γ时，承租方将拒绝续租。若租赁延迟时间为t0，租赁延迟期间对设备故障进行小修，则租赁延迟成本为

综上，优化出租方维护的总费用模型即为

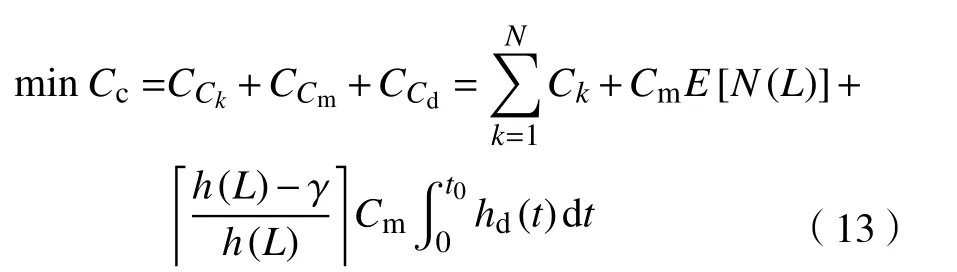
2.3 承租方总的工件加工时长优化模型

在租赁期内，有m个 工件的工件集J={j1,j2,j3,···,jm}，并且对设备运行期间出现的故障采取小修。对于决策变量Pi， 如果工件i加工结束时进行预防性维护，则Pi=1， 否则，Pi=0；对于决策变量Ri，如果工件i加工结束时进行更换操作，则Ri=1， 否则，Ri=0。

为解决工件加工时长优化问题，可将维护活动当作一种特殊的工件与加工工件一起进行排序[10]。排序时尽量减少预防性维护和更换操作可降低总加工时长，但会造成故障停机增加，虽然小修时间忽略不计，但是频繁的停机小修会影响承租方的正常生产活动。因此，优化目标为在允许的最大停机次数内，最小化工件总的加工时长，具体如下：

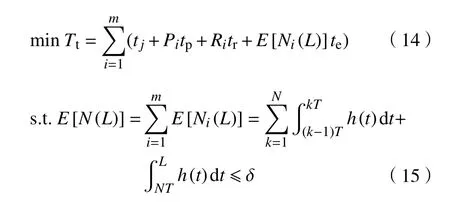
式中：Tt为 维护活动总时长；tj为单个工件的基本生产时间；Pi为 工件i加工结束时是否进行预防性维护的决策变量；tp为单次预防性维护的时间；tr为单次更换维护的时间；te为单次故障小修维护的时间，E[Ni(L)]te表 示租赁期内加工工件i期间的故障小修时间； δ为租赁期间承租方能够允许的最大小修次数。

2.4 承租方满意度优化模型

本文针对租赁设备，通过响应模型[7,11]，得到维护周期内产品合格率的变化情况。引入Y1(t),Y2(t),···,Yw(t)表示产品的多个质量特征随时间的衰退量，可表示为

式中： φg为常数；bg和dg分 别为表示X(t)和Z线性影响系数的向量组；Z为噪声变量，服从正态分布，Z～N(0,∑Z)； Γ为表征X(t)和Z交互影响的系数矩阵；X(t)ΓZ表示可控过程变量和噪声变量的交互效应。

由于t时刻Xs(t)的 不确定性，Yg(t)也是随机的，则产品的合格率F(t)可表示为

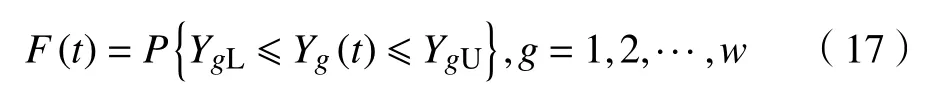
式中，YgL和YgU分 别为Yg(t)的 上下限，Yg(t)为X(t)和Z的响应。

由于X(t)和Z的分布已知，且相互独立，故式（17）可转化为X(t)和Z的积分。假设租赁设备的生产速度为常数r，则维护周期内生产的合格品数表示为

用平均合格品率来表示承租方满意度，则可描述为

2.5 租赁双方多目标维护建模

实际生产中，在多目标决策中整合优化设备总维护费用、总的工件加工时间和满意度，即最小化出租方的设备总维护费用（ m inCc），最小化设备承租方总的工件加工时间（ minTt），最大化承租方的满意度（ m axF(t)） ，需要统一Cc,Tt和F(t)的量纲和优化方向。为使优化决策统一为最小化问题，将上述指标进行归一化处理，并提出多目标优化指数概念，将多个维护活动衡量指标整合为一个综合的指标，即多目标优化指数W。在目标函数中引入表达式考虑权重因子 ω1, ω2和 ω3（ ω1+ ω2+ω3=1），则在租赁周期内，确定预防性维护时间间隔的最优值，使得目标函数最小。多目标决策模型的目标函数为

式中：Cc*为最小化式（13）所得的出租方设备总维护费用的最优值；Tt*为最小化式（14）所得的设备承租方总的工件加工时间的最优值；F(t)*为最大化式（18）所得的承租方满意度最优值。

由微积分原理可知，在各预防性维护周期内，单一维护决策模型（式（13）、式（14）和式（18））以及多目标模型（式（19））存在有限且唯一的最优值Cc*，Tt*，F(t)*。首先输入初始值和权重因子的值；其次，根据单一出租方的设备总维护费用模型（式（13））、设备承租方总的工件加工时间模型（式（14））、承租方的满意度模型（式（18）），分别对预防性维护时间间隔求导，推得函数极值，可求解得到最优值Cc*，Tt*，F(t)*；最后以单一目标最优化决策结果为输入，多目标预防性维护决策模型（式（19））推得函数极值，求解得第k个维护周期的最优预防性维护时间间隔。

3 算例分析

3.1 数据准备

根据Weibull 分布的故障率表达，结合设备故障率与相关部件质量衰退影响，在租赁双方联合优化的目标下，根据以往文献中的参数估计方法和此前研究中的实验数据[12-13]，结合设备的历史数据，表达式中的故障率参数取值为α=2.46, η=104.3, β1=0.018 7, β2=0.033 6, θ1=4.13, θ2=2.96, μ1=0.001 56, μ2=0.001 3。

在租赁双方联合优化模型中，需考虑承租方生产时间优化。某些维护成本理想的优化方案可能会造成频繁的停机小修，同时对承租方的生产活动带来较大影响。因此，在选择优化维护方式时，应将停机小修次数约束在承租方可接受范围内。在对T（单位：d）进行全租赁期内优化时，经过数据分析，在（0, 200）内小修次数呈现规律性下降，超出此区间后，小修次数会急剧上升。因此第一次进行设备状态检测并确定维护方式的时间节点不能超过200 d，此时小修次数E[N(L)]的值为318.95。因此，取停机小修次数的阈值δ=318，即

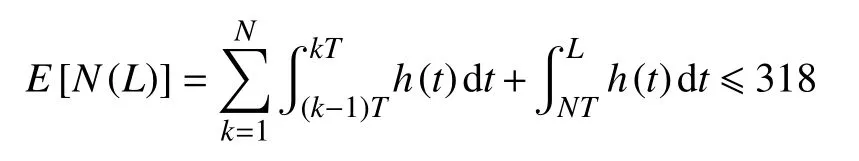
3.2 考虑维护成本的结果分析

设备小修费用、预防性维护费用及更换费用根据出租方的维护数据得到；各类小修、预防性维护和更换的惩罚成本由承租方对维护活动造成的损失进行评估，并与出租方协商确定。预防性维护阈值 ε1、 更换阈值 ε2根据同类型设备数据整理确定。租赁延迟参数通过阅读相关研究成果确定[12-13]，企业续租阈值 γ通过研究承租方续租历史数据确定[13]。上述参数的具体取值为Cm=300,Cp=600,Cr=1 500, ε1=0.5, ε2=0.85, μ=0.5,t0=50, γ=0.5,L=1 200。

根据上述约束条件，在区间（0，200）内，对检测维护周期T进行优化。在区间（0, 200）内只考虑优化维护成本时，运用编程计算并画出维护费用折线图如图1 所示。

图1 仅考虑维护费用优化的维护成本Fig.1 Optimized maintenance cost considering only maintenance cost

由图1 可知维护费用变化趋势是随着检测维护间隔周期T的增加逐渐下降，但在整体下降趋势下，仍存在小范围的回升。从全周期计算结果观察得出，在检测维护周期T=172 时，总维护费用最小，Cc*=90 478.45。截取仅考虑维护费用的维护成本，部分计算结果如表1 所示。

表1 仅考虑维护费用的维护成本部分计算结果Tab.1 Calculation results of the maintenance cost part considering only maintenance cost

3.3 考虑加工时间的结果分析

在加工时间优化模型中，将每个工件的不可分割的加工时长记为1 单位时间，总的设备租赁生命周期为L=1 200 d。为减小维护活动对生产计划的影响，建模中求最小加工时长的优化目标在本算例中可进行变形转化。算例中将工件时长的相关优化目标转化为降低在设备的整个租赁周期内的总检测维护活动时长。在检测维护周期Tϵ（0，200）时，计算不同检测维护周期下设备维护活动的总时长，维护活动时长计算参数为tp=3,tr=15,tj=1,te=2。

租赁期L=1 200 内，计算不同检测维护周期对应的维护活动总时长变化趋势，如图2 所示。

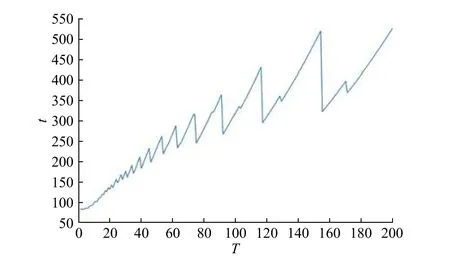
图2 不同检测维护周期对应的维护活动总时长Fig.2 Total duration of maintenance activities corresponding to different inspection and maintenance cycles

由图2 可看出，随着检测维护周期的变长，设备的维护活动时间呈螺旋上升趋势。在检测维护周期较小时，由于发现问题较为及时，因此，根据检测故障结果可以及时利用小修恢复生产，预防性维护和更换操作都较少，且单个周期内的意外故障停机小修也较少，因此总的维护时长也较短。根据计算结果，若只考虑维护时间最小化，则检测维护周期应尽可能的小，检测维护操作应该尽可能的频繁，但是，这显然与优化生产计划的目标不一致。根据式（15），即总小修次数阈值 δ对小修次数约束，可知仍需对小修次数进行限制，以防止维护活动无休止地中断生产。根据计算可知，在设备的租赁周期内，设备的意外停机小修次数与检测周期小修维护次数之和结果，如图3 所示。

图3 租赁周期内总停机次数Fig.3 Total number of downtimes during the lease period

由图3 可知，检测维护周期较短时，设备停机非常频繁，会经常导致生产中断。随着检测维护周期变长，设备停机次数逐渐降低，对生产活动的影响逐渐减小。但是随着检测维护周期的继续变长，设备状态下降，故障率累积，而过长的检测维护周期导致问题得不到及时解决，设备的停机次数也会随着检测维护周期的变长而增加。因此，租赁期内总的停机次数呈现先下降而后又逐渐回升的趋势。根据对小修次数的限制，应当在T∈(3,200)内，对设备总维护时间进行优化。结合图2 中维护活动总时长的变化趋势，截取部分维护活动总时长计算结果，如表2 所示。

表2 部分检测维护周期对应的维护活动总时长Tab.2 Total duration of maintenance activities corresponding to part of the inspection and maintenance cycle

根据上述图表结果及分析可知，若只考虑加工时长因素，即尽可能压缩维护活动总时长，最优选择是T=4 时，总的维护活动时长约为Tt=86.51。但是当T=4 时，设备的总维护费用Cc=123 805.89，这一结果高出最优维护费用Cc*=90 478.45 较多。由此可见，考虑维护费用优化角度和维护时间优化角度所得的优化结果并不统一，以及后续考虑产品质量优化的维护方案制定也会与上述两个方面的优化结果有所差异。

3.4 考虑产品质量的结果分析

设备维护对产品质量影响的分析中，相关组件质量对产品质量的影响更为严重，相关组件质量的状态不仅对设备的故障率产生影响，而且可能会造成产品质量偏差。本例中考虑以一种加工中心加工一种圆柱齿轮外壳为例，圆柱齿轮外壳用于连接减速机、减速机中的差速器和差速器总成。圆柱齿轮外壳对减速机和差速器的性能有显著影响。随着该设备役龄的增加，钻孔刀逐渐磨损，钻孔刀的长度逐渐产生偏差，在当前工序上进行加工的工件可能会逐渐偏离标准值，因此，钻孔刀是与质量相关的组件。钻孔刀具的长度为可调整的过程变量，可记为X(t)；钻孔刀工序深度的误差即为产品的质量特征随时间的衰退量，可记为Yg(t)。钻孔刀的振动会影响该工序的深度，振动的振幅可认为是一个噪声变量，记为Z。钻孔刀在全新状态时的磨损量为0，即X(0)≡0,Z～N(0,0.01)。该工序中钻孔刀作业的标准长度为50mm，其误差区间为(-0.025,0)，即t时刻产品合格率为通过响应曲面法得到模型。

根据模型计算得到产品合格率P受检测维护周期变化影响如图4 所示。

根据计算结果，随着检测维护周期的变长，设备故障状态的累积，导致产品合格率逐渐下降。其中，当T> 189 时，产品合格率低于80%，产品合格率低于80%被认为是不可接受的，则根据产品合格率要求，应在区间（1, 189）对设备维护检测周期进行优化。

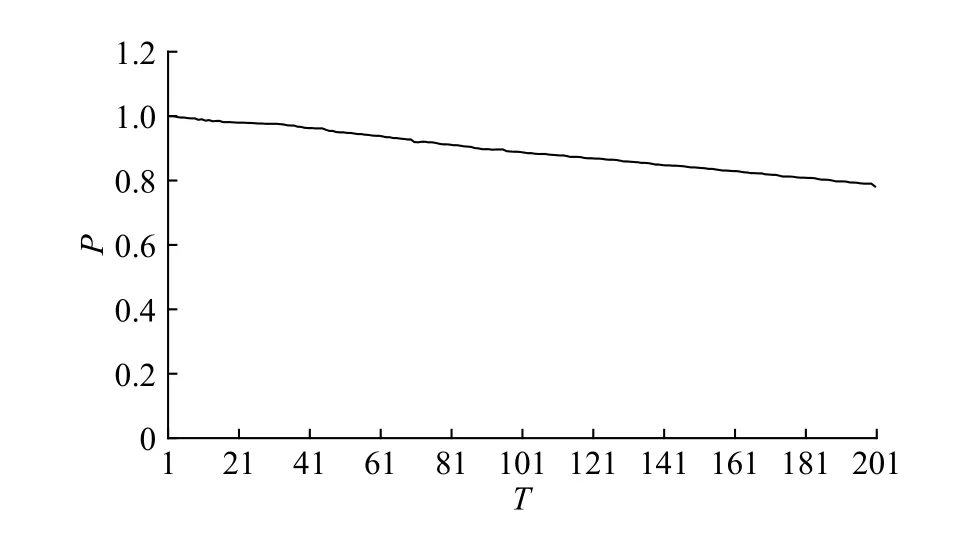
图4 产品合格率随检测维护周期变动的变化趋势Fig.4 Change of product qualification rate with the inspection and maintenance cycle

3.5 多目标结果分析

基于专家经验，将出租方角度考虑的维护成本的权重赋值为0.5，设备维护活动时长权重赋值为0.25，设备维护对产品质量的影响权重赋值为0.25。在实际的设备租赁活动中，租赁双方可根据实际的市场情况以及具体设备的维护要求调整各个指标的权重，并在前期签订租赁协议时作出明确的规定。根据上述权重取值，多目标优化指数随检测维护周期变化趋势如图5 所示。

图5 多目标优化指数变化趋势Fig.5 Trend of multi-objective optimization index

由图5 可知，多目标优化指数首先随检测维护周期的增加而上升，达到最大值，当多目标优化指数达到最大值时，说明在此检测维护周期下，租赁双方对维护计划的安排是最为满意的。而后多目标优化指数开始随着维护周期的继续增大而下降，并且在下降的过程中有所反复，但始终不高于此前的峰值水平。因此，显然多目标决策 ω1=0.5， ω2=0.25和 ω3=0.25是3 个决策目标的融合折衷，且多目标决策模型可以扩展到任意数量。

根据计算结果，当检测维护周期T=22 时，多目标优化指数值最高，为0.881 8，即此时租赁双方的经济利益最优。

3.6 对比分析

为了体现本文多目标预防维护决策模型的优越性，将其与传统的以成本为目标的维护决策模型进行比较。若只考虑出租方所承担的设备维护总费用，检测维护周期取值为T=172 时，多目标优化指数为0.777 5，此时设备总的维护成本虽然最低，但是在该维护计划中，设备维护活动总的时长达到Tt=373.53 d，产品合格率也降至81.81%，因此设备承租方对如此大的检测维护周期接受度低。可见，以维护成本、加工时间和满意度为导向，模型在保证维护效率和质量提升上都有更好的表现。这也验证了以维护时间间隔为优化目标的有效性，能有效评估设备可靠性和产品质量多项指标，并较好地平衡维护的投入和产出，满足企业的实际维护需求。

若从承租方的角度考虑，缩短检测维护周期将能保证较少的设备维护时间，以及较高的产品合格率。但是，当检测维护周期缩小到一定程度时，维护费用将会急剧增长，这对于出租方来说是难以接受的，故而应找到双方诉求的平衡点，以保证双方共同的经济利益，以及稳定的合作。

4 结 论

针对当前租赁市场上仅考虑维护成本优化，难以适应当前租赁市场上设备承租方对设备维护活动的要求的情况，本文提出综合设备出租方的设备维护费用、设备承租方对设备维护活动时长的要求，以及设备维护活动对产品质量的影响，联合优化租赁双方的经济利益诉求。同时，维护方式采取多维护策略。计算不同检测维护周期对应的维护活动造成的费用、维护活动时间，以及维护活动对产品质量的影响，而后进行归一化处理，并对三者赋予相应的权重系数，以多目标优化指数综合评价租赁双方对维护计划的满意程度。通过实例分析呈现了决策过程，并说明了本文中联合考虑租赁双方对维护活动的要求更加符合实际的市场需求。

本文的研究可为租赁市场上租赁双方共同制定合理的维护计划提供一定的指导，未来可以考虑在租赁双方联合优化下租赁设备的状态维护策略。