求解全局优化问题的改进灰狼算法
2021-03-25周溪召
张 阳, 周溪召
(上海理工大学 管理学院,上海 200093)
元启发式算法是一类在特定的资源(时间等)约束条件下求解问题近似最优的优化技术,具有简单、高效和计算成本小等优点。自1983 年Kirkpatrick等提出模拟退火算法(simulated annealing algorithm,SA)[1]和1992 年Holland 提出遗传算法(genetic algorithm, GA)[2]以来,众多学者投入到这一研究领域。经过几十年的发展,许多元启发式算法相继被提出并已广泛应用于研究领域和实际场景,如粒子群算法(particle swarm optimization, PSO)[3]、蚁群算法(ant colony optimization, ACO)[4]、引力搜索算法(gravity search algorithm, GSA)[5]、蘑菇繁殖算法(mushroom reproduction optimization, MRO)[6]、人工蜂群算法(artificial bee colony algorithm, ABC)[7]、教学优化算法(teaching-learning-based optimization,TLBO)[8]和哈里斯鹰算法(Harris hawks optimization,HHO)[9]等。但是,根据没有免费的午餐定理(NFL)[10],没有一种算法适用于求解所有问题,因此,仍有必要对元启发式算法进行进一步的研究。
在文献[6]中,元启发式算法可以根据不同的灵感来源而分为3 类:群智能算法、非群智能算法和物理/化学算法。2014 年Mirjalili 等[11]受自然界中灰狼领导等级制度和群体狩猎行为启发,提出了一种新的群智能算法—灰狼算法(grey wolf optimization, GWO)。灰狼算法是一种强大的优化技术,已被成功应用于许多领域。谭念等[12]提出了一种基于灰狼算法和支持向量机(GWO-SVM)的木材密度预测模型,为杉木性质定量分析提供了理论依据;姚鹏等[13]提出了一种基于改进的扰动流体动态系统与灰狼优化理论的混合航路规划算法,为复杂地形环境下的无人机三维航路规划问题提供了解决方案;王书芹等[14]提出了基于灰狼优化算法的长短期记忆模型(long short term memory, LSTM),解决了传统LSTM 易于收敛到局部最优的问题。
然而,同其他元启发式算法一样,灰狼算法也存在着收敛速度较慢、求解精度不高、在一些复杂问题上容易陷入局部最优等缺点。为提升GWO 的性能,许多学者进行了相关研究。Joshi等[15]提出了一种基于精英策略的增强灰狼算法(enhanced grey wolf optimization, EGWO);Heidari等[16]提出了结合列维飞行和贪婪搜索机制的灰狼算法(levy-embedded GWO, LGWO);文献[17]提出了基于模糊层次算子的灰狼算法,并提出了两种个体位置更新时的比例权重策略;Saremi 等[18]提出了基于进化种群动力学(evolutionary population dynamics, EPD)的灰狼算法(GWO-EPD),EPD 要求表现不佳的搜寻个体进行动态的位置调整;王敏等[19]提出了一种基于反向学习策略、非线性收敛因子和变异算法的新型灰狼算法(novel GWO,NGWO)。在GWO 中,收敛因子a在一定程度上决定了算法局部开发过程和全局搜索过程之间的平衡。本研究首次提出了一种新的指数变化形式的收敛因子,而且与以前的所有针对a的改进之处所不同的是:提出的收敛因子最终并不会减小为0。同时为了加快算法的收敛速度,重新定义了灰狼算法中的 α,β,δ狼,并提出了一种基于自适应调整策略的灰狼位置更新公式。此外,针对文献中提出的动态权重策略进行修订,以获得更好的求解性能和鲁棒性。最终,使用了10 个典型的基准测试函数验证了以上改进策略的有效性。
1 灰狼优化算法
灰狼优化算法是一种较新的优化技术,其主要思想是灰狼群体中的领导等级制度和群体狩猎模式。在自然界中,灰狼群体具有森严的社会等级制,如图1 所示,狼群中所有个体划分为4 个等 级: α,β,δ 及 ω。 α是 狼 群 的 领 袖; β仅 次 于α,其职责是辅助头狼 α制定决策及其他群体性活动;接下来是δ,狼群中的侦察兵、哨兵、长老、狩猎者及看守者都属于此类;等级最低的狼则为ω。除等级制度外,小组狩猎也是灰狼种群中一个有趣的社会行为。
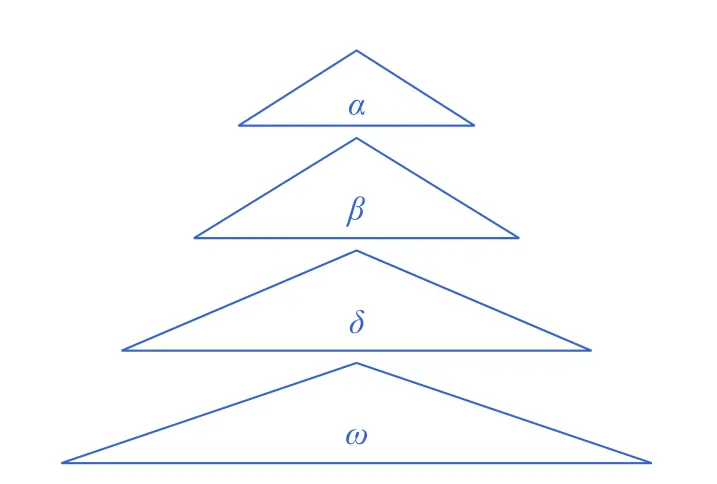
图1 灰狼种群社会等级结构Fig.1 Social hierarchy structure of grey wolf population
在GWO 中,适应度值最优的个体被视为 α,适应度值第二和第三的分别被定义为 β 和 δ,其余个体均为 ω。在算法实施中,以下等式用来描述灰狼种群包围猎物的行为:

式中:t表示当前迭代次数;X(t)表示灰狼个体;Xp(t)表示当前的灰狼个体;D表示个体与猎物之间的距离;A和C是系数向量,分别用式(3)和式(4)来计算。

式中:r1,r2是0~1 之间的随机向量;a表示收敛因子,可用等式a=2×(1-t/T)来计算,T为设定的最大迭代次数。
在狩猎时,GWO 假定 α,β,δ 对于猎物的潜在位置更具有感知性,所以,灰狼个体会分别判断自身与α ,β,δ 之 间的距离Dα,Dβ,Dδ(式(5)),分别计算其朝向三者的移步距离X1,X2,X3(式(6)),并最终在向着三者的包围圈之内进行移步,移动公式为式(7)。

2 改进的灰狼优化算法
2.1 指数规律收敛因子调整策略
全局搜索能力和局部开发能力是描述元启发式算法性能的两种通用属性,如何有效平衡两者也是元启发式算法首要思考的问题。全局搜索是指在整个搜索空间搜寻最优解,强的全局搜索性可使算法有效避免陷入局部最优,增强算法的寻优能力;局部开发能力是指在局部区域进行精确搜索,强的局部开发性能够提升算法的求解精度、加快算法收敛速度。一般情况下,迭代的前期使用全局搜索策略,而在后期则使用局部开发策略。在GWO 中,当|A|>1 时,灰狼种群在整个搜索域搜寻潜在猎物;当|A|<1 时,灰狼种群将逐渐包围并捕获猎物。而A的值取决于收敛因子a的变化情况。
在GWO 中,a随迭代的更新方式采用一种线性递减策略,可用等式a=2(1-t/T)进行计算。在Chiu 等[20]的研究中已经证明重要参量的不同更新策略会极大影响算法的性能,而且线性策略往往不是最有效的。因此,本文提出了一种新的基于指数规律变化的收敛因子更新方式,如式(8)所示。

如图2 所示,线性表示GWO 中所使用的收敛因子更新方式,指数形式表示本文提出的新的收敛因子更新方式。
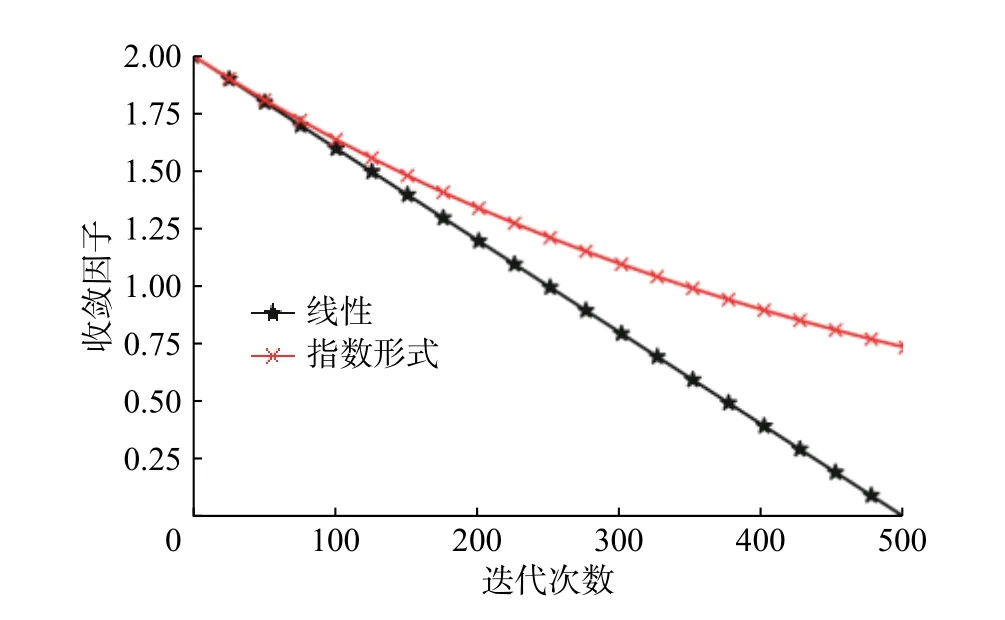
图2 两种收敛因子Fig.2 Two convergence factors
2.2 自适应位置更新策略
在GWO 中,初始化 α,β,δ 三组解会被记录并保留,直至在迭代的过程出现适应值更好的个体代替它们为止。就是说,如果在第t代,种群中未出现优于记录的 α,β,δ的解时,当前的种群依然向着这三只狼更新位置。然而,当这三者全部陷入局部最优时,此时整个种群就难以寻求更好的解。可以理解为:当狼群的决策者误判了猎物出现的地方,那么,所有灰狼的包围动作都将是无效的,它们难以在错误的地方找到猎物。
本文提出了一种新的 β 与 δ的定义方式以强化当前代最优个体的作用,从而提升算法的全局搜索能力。在算法实施中, α同GWO 一样,但是,β与 δ被 定义为局部变量,它们是第t(t=1,2,···,T)代中的适应度值最优和第二的灰狼个体。
同时,为了更好地平衡算法的全局搜索和局部开发过程,本文提出了一种新的自适应的移步策略,其数学表达为

2.3 修订的动态权重策略
在文献[17]中指出了GWO 位置更新公式的缺点,X1,X2,X3求平均值的方式无法凸显α,β,δ三者之间的重要度,为此,作者提出了两种新的比例权重策略,分别是加权平均策略和基于适应度值的比例权重策略,并进行了实验验证。文献[21]提出了一种基于指导位置向量权值的动态比例权重。文献[22]对不同的权重策略进行了分析与实验研究,并从理论上证明了动态权重策略能高效寻优的原因。
当前灰狼个体到 α ,β,δ之间的距离权重

最终,灰狼位置更新公式可表示为
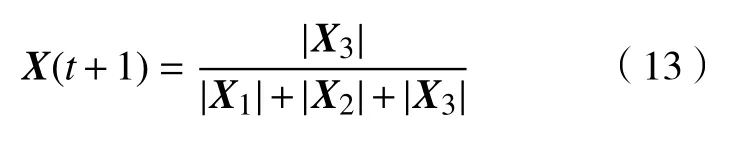
然而,在实际应用中,式(10)~(12)很可能出现分母为0 的情况。因此,需添加一个很小的常数ε,取值为10-16。它们被修改为
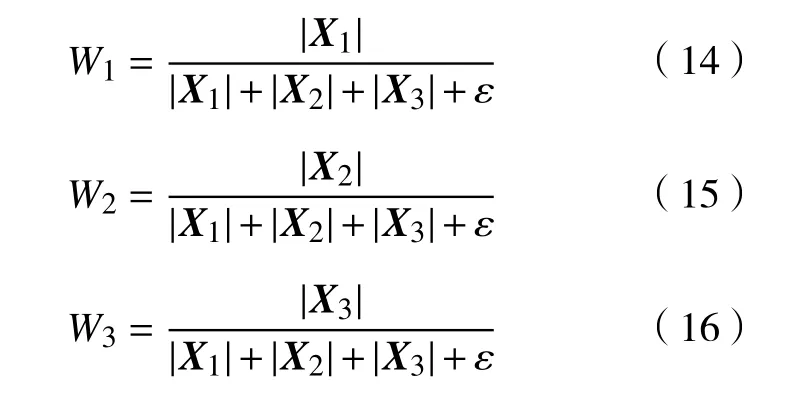
结合前面的自适应位置更新策略,最终的灰狼位置更新方式可表示为
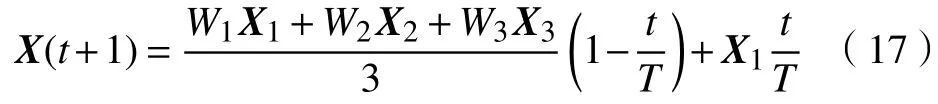
2.4 MGWO 算法步骤
综合使用以上3 种改进策略,本文提出的改进灰狼优化算法(MGWO)步骤如下:
a.参数初始化。设定种群规模N,总迭代次数T,常数ε;初始化a,A,C。
b.在待解问题的搜索空间内随机生成灰狼初始种群。
c.计算种群中所有灰狼个体的适应值,选择适应度值最优的个体,并记录其位置为Xα。 令t=1,迭代开始。
d.判断算法是否满足终止条件,若满足,则输出最优解;否则,执行步骤e。
e.根据式(8)计算收敛因子a。
f.灰狼种群按适应度值排序,排在前两位的位置分别被记录为Xβ和Xδ。
g.根据式(14)~(16)计算动态比例权重,灰狼个体根据式(17)更新位置。
h.将超出搜索空间的灰狼个体放回搜索空间。
i.更新Xα, 令t=t+1,返回步骤d。
3 实验与分析
为了实验验证提出的3 种改进策略的有效性,选取了国际上通用的10 种基准测试函数进行仿真实验。实验运行环境为Intel(R)CPU 3550M,主频2.30 GHz,内存4 GB,Windows 10 64 位操作系统,所有代码通过Python 3.7 进行编程。在此基础上,进行了3 组对比实验。为保证无偏性,所有算法的种群数N均设定为30,总迭代次数设定为500。为了排除随机性的影响,所有实验独立运行30 次,取30 次的平均值和标准差作为算法性能的度量标准。
3.1 基准测试函数
基准函数的数学表达如表1 所示,包括7 个单峰测试函数(F1~F7)和3 个多峰测试函数(F8~F10)。单峰测试函数是算法求解精度和收敛速度的度量,而多峰测试函数可以很好地表示算法的全局搜索能力和避免局部最优的能力。部分测试函数的3 维图像如图3 所示。

表1 基准测试函数Tab.1 Benchmark function

图3 部分基准函数的二维搜寻空间Fig.3 Two-dimensional search space of a part of benchmark function
3.2 与GWO 和其他改进灰狼算法的比较
为了测试算法的搜寻性能,将提出的策略与其他文献的策略进行比较。各比较算法及其描述如表2 所示。实验结果如表3 所示。表3 中列出了各算法在基准测试函数上的测试结果。表格中粗体显示的是最佳求解结果。表2 中从EGWO 到GWO-Fuzzy 的实验结果直接来源于文献[15-19]。其中,EGWO 的实验环境为QT Creator 2.4.0;LGWO实验运行环境为Intel(R)Core i2,主频2 GHz,内存4 GB,Windows 7 64 位操作系统,编程软件为Matlab R2013a。
从表3 可以看出,提出的MGWO_1,MGWO_2算法在函数F1~F4 和F6~F9 上均优于GWO 算法,而且在大多数问题上略优于其他文献提出的改进灰狼算法,这说明了提出的改进策略的有效性。同时,依据数值结果,MGWO_2 相比MGWO_1获得更高的求解精度,这说明灰狼个体的自适应位置更新策略是一种更优的改进策略。

表2 对比算法及描述Tab.2 Comparison algorithms and its description
MGWO_3 综合使用了指数规律收敛因子调整策略和自适应位置更新策略,从结果可以看出,在函数F1~F4 上,MGWO_3 明显优于除MGWO_4外的其他对比算法。在函数F7 上,MGWO_3 排在MGWO_4 和NGWO 之后,胜过其他8 种对比算法。在函数F8 上,MGWO_3 仅次于MGWO_4,NGWO 和LGWO。在函数F9 上,MGWO_3 仅次于MGWO_4 和LGWO,优于其他8 种算法。但是,在F6 和F10 上,MGWO_3 的结果并不理想。
MGWO_4 结合了本文提出的3 种改进策略,从表3 可以看出,它在函数F1,F3,F8 和F10上均收敛到理论最优值。在函数F2,F4,F7 和F9 上,其求解精度明显优于其他算法。然而,对于函数F5 和F6,MGWO_4 表现一般。
在所有测试函数上各算法30 次独立运行的运行总时间列于表4。从运行时间来看,在函数F1~F4,F7 和F8 上,GWO_EPD 所耗费的时间成本最小。在函数F5 上,MGWO_2 的运行时间要小于其他的对比算法。在函数F6,F9 和F10 上,GWO 的运行时间最短,优于其他算法。在函数F7 和F8 上,GWO_EPD 的运行时间依然具有竞争性。

表3 11 种对比算法在10 个测试函数上的实验结果Tab.3 Experimental results of 11 comparison algorithms on 10 test functions
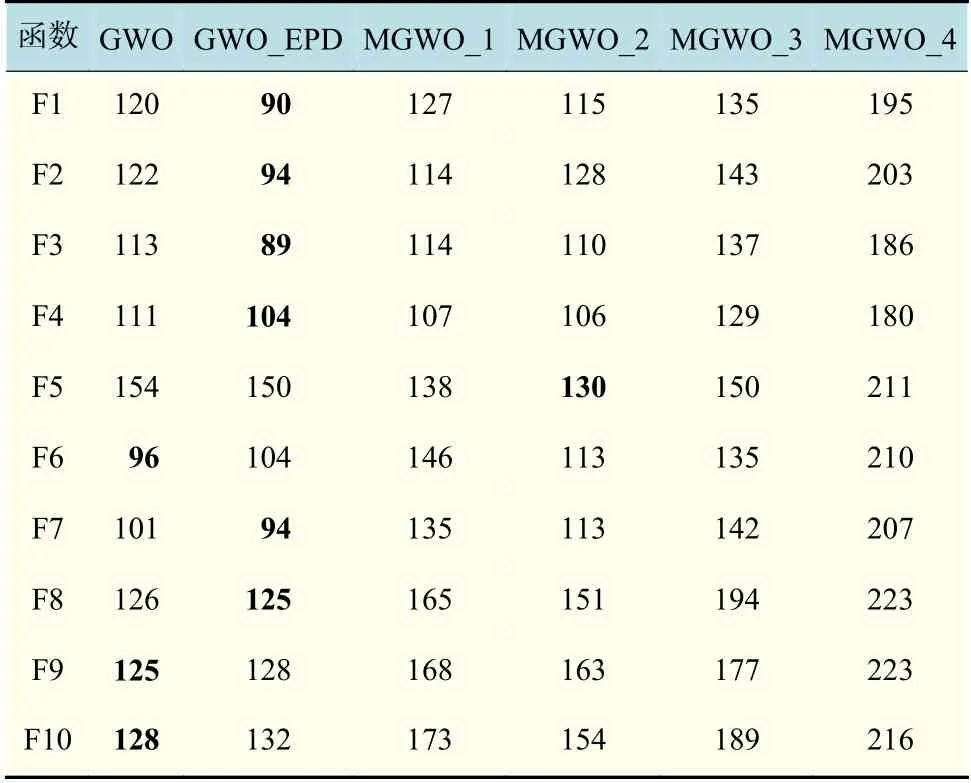
表4 对比算法运行时间Tab.4 Running time of the comparison algorithms
综上所述,本文提出的3 种改进策略都是有效的。综合所有数值结果,MGWO_4 明显优于其他10 种对比算法,它具有很高的寻优能力,获得了较高的求解精度,同时从标准差来看,具有较高的鲁棒性。MGWO_3,NGWO 和LGWO 仅次于MGWO_4,它们在特定的问题上表现突出,且都明显改进了GWO 算法的性能。但是,也应该认识到,MGWO_4 和MGWO_3 高效寻优结果的代价是一定程度上时间成本的增加。而MGWO_1 和MGWO_2 可能是最佳选择,它们对GWO 的性能提升幅度不如MGWO_4 和MGWO_3 那么大,但运行时间无明显变化。具体选择哪种算法,使用者要视自己的需求情况而定,如果对待求解问题的精度要求较高,MGWO_4 和MGWO_3 算法显然是更好的选择。
3.3 与其他元启发式算法的比较
为进一步验证本文改进策略的有效性,将表现较佳的MGWO_3,MGWO_4 与GA,TLBO,HHO 进行对比实验。其中,GA 和TLBO 是经典的优化算法,HHO 是该领域最新的研究成果。其中,对于GA,使用轮盘赌的染色体复制策略、均匀杂交策略和随机选择突变3 种策略来进行编码,染色体交配概率设置为0.8,突变概率设为0.3。其余算法均只有种群规模和总迭代次数2 个通用参数。实验结果如表5 所示。
从表5 中的数值结果可知,对于函数F1 和F3,MGWO_4 在500 次迭代内收敛到理论最优值0,远远优于其他的优化算法;对于函数F8 和F10,MGWO_4,TLBO 和HHO 这3 种算 法 均达到理论最优值0,但是,从收敛曲线(图4)可以看出,MGWO_4 的收敛速度明显高于TLBO 和HHO,所以,它依然是最佳算法;对于函数F2 和F4,MGWO_4 分别得到了3.14E-205 和1.23E-181 的最优解,其求解精度相当高,远胜于其他的优化算法;对于函数F5 和F6,HHO 算法取得了最好的寻优结果,其次是MGWO_3 与MGWO_4;对于函数F7,MGWO_4 获得最佳求解结果,其次是TLBO 与MGWO_3。值得注意的是,对于8 个基准函数(F1,F2,F3,F4,F7,F8,F9,F10),MGWO_4 不仅取得了最优的平均值,而且其标准差也是最小的,这说明了MGWO_4 算法具有较高的鲁棒性。
表6 列出了GA,TLBO,HHO,MGWO_3 和MGWO_4 在10 个测试函数上30 次运行的总时间。从表6 中的数据可以看出,TLBO 和HHO 算法的求解时间明显优于其他的对比者,特别是对于单峰测试函数,这两种算法的运行时间很短。而MGWO_3 和MGWO_4 算法的运行时间相对较长。
6 种算法(GWO,GA,TLBO,HHO,MGWO_3 和MGWO_4)在部分测试函数上的收敛曲线如图4 所示。由图4 可知,MGWO_3 提升了GWO的收敛速度和求解精度,MGWO_4 具有相当高的收敛速度和求解精度,远优于GWO 和其他的对比优化算法。
以上两组对比实验验证了本文提出了的3 种改进策略的实施效果,从运行时间来看,MGWO_1和MGWO_2 在提升GWO 的性能的基础上运行时间无明显变化,而MGWO_4 和MGWO_3 虽然在求解精度和收敛速度上有大幅度的提升,但带来了程序运行的时间成本的增加。综上所述,可以看出本文提出的MGWO 算法依然是一种更好的优化算法。

表6 5 种对比算法在10 个测试函数上的运行时间Tab.6 Running time of the 5 comparison algorithms on 10 test functions
3.4 拉伸/压缩弹簧设计优化问题
以上两组对比实验所针对的问题都是无约束优化问题,为进一步验证本文改进策略的有效性,使用约束优化问题继续进行实验。拉伸/压缩弹簧设计优化问题是一个经典的带约束的工程优化问题,该问题的目的是在满足3 个设计变量的4 个约束条件的情况下求得弹簧重量的最小值。3 个设计变量分别是线径d,平均线圈直径D和有效线圈数N;4 个约束条件与剪应力、弹簧颤动频率和最小挠度相关。图5 描述了这一问题和其设计变量,该问题的数学表达如下:
设计变量

优化函数
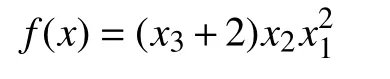
约束条件:
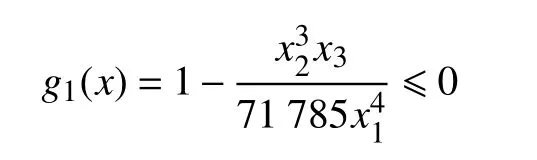
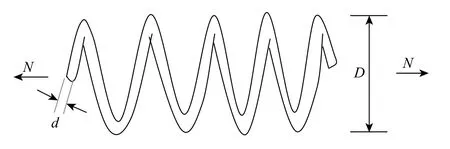
图5 拉伸/压缩弹簧设计优化问题Fig.5 Tension/compression spring design problem

设计变量范围:

使用7 种对比算法来求解这一约束优化问题,算法在30 次实验中所获得的最佳实验结果如表7所示。从表7 中的数据可以看出,MGWO_2 取得了最好的结果,优于其他对比算法。MGWO_1 和MGWO_3 的数值结果也要优于GWO 和其他算法。MGWO_4 虽然在无约束优化问题时表现突出,但在求解拉伸/压缩弹簧设计优化问题时不如其他3 种MGWO 算法和GWO 算法。
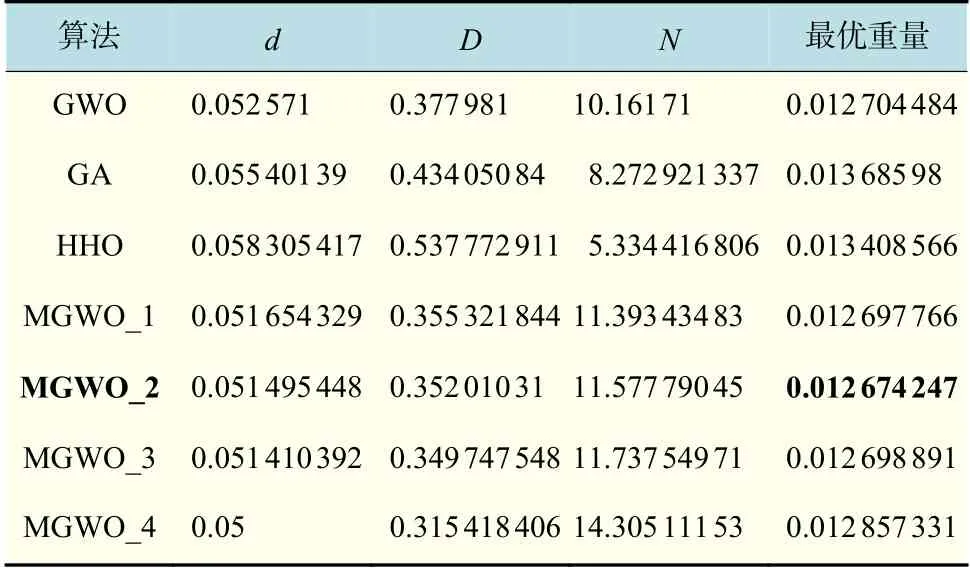
表7 拉伸/压缩弹簧问题的结果比较Tab.7 Comparison of results for the tension/compression spring problem
4 结束语
针对基本GWO 求解精度不高、收敛速度较慢和易于陷入局部最优的问题,提出了一种改进的灰狼优化算法。首先,提出了一种收敛因子指数变化规律的修正策略,处于这种策略下,a在迭代末期并不会减小为0,实验结果验证了其有效性。其次,通过重新定义 β 和δ 而强化每代最佳搜寻个体的作用,进而提出了一种灰狼个体自适应位置更新策略。此外,引入动态权重策略,并对其进行了修订。接着,针对无约束优化问题的对比测试实验证明了改进策略的有效性,尤其是综合使用3 种改进策略的MGWO_4 具有较强的局部最优避免性、较快的收敛速度、较高的求解精度,它明显提升了基本GWO 的性能,更好地平衡了算法的全局搜索性和局部开发性。最后,对于工程设计约束优化问题的实验结果进一步证明了本文提出的MGWO 的有效性。
未来的研究思路是编写二进制的MGWO,并将MGWO 运用到更多的实际问题中。
