基于Prophet-LSTM-PSO 组合模型的医院住院量预测研究

徐 佩, 樊重俊, 朱人杰, 黄 耐

（1.上海理工大学 管理学院，上海 200093；2.同济大学附属东方医院，上海 200120）

2019 年末我国武汉地区爆发新型冠状病毒肺炎，由于爆发在春运期间，严重性不言而喻。举全国之力共抗疫情，但在武汉地区，医院可供床位却远远不足。虽然这属于突发事件，但同时说明对医院住院量的研究非常必要，通过对医院住院量未来动态变化的预测研究，可以提高医院床位的使用率，合理配置各科室医疗床位，最大限度发挥现有医疗资源的作用。

在医疗床位的预测方法中，时间序列预测方法是较为常用的预测方法，并在多种实际应用场景中预测效果较好[1]。2008 年徐建伟[2]建立了贝叶斯正规化BP（back propagation）神经网络，对医院床位数据进行拟和预测，并与指数平滑和自回归模型进行比较，实验结果表明，贝叶斯正规化BP 神经网络模型较传统模型预测的精度更高一些。2013 年龙会典等[3]建立了由自回归移动平均模型（ARIMA）、灰色动态模型（GM 模型）和BP 神经网络集成的时间序列预测模型。首先建立GM（1，1）模型，对序列的趋势项进行预测，然后建立基于ARIMA 和BP 神经网络的组合模型，对序列的周期波动项进行预测，最后利用乘积模型集成两者预测值。实证结果表明，集成模型的预测效果显著高于单一模型。2014 年曹净等[4]提出了一种基于小波变换、粒子群优化的最小二乘支持向量机（PSO-LSSVM）和ARIMA 的基坑变形时间序列预测方法，并成功地应用于昆明某基坑工程的深层水平位移预测中。综合以上研究表明，组合预测模型在不同领域的预测效果均优于单一模型的预测效果。

本文针对上海市东方医院呼吸内科住院量的时间序列数据进行研究，提出了一种基于Prophet-LSTM-PSO 组合模型的预测方法，分别运用先知模型（Prophet）和长短期记忆循环神经网络（LSTM）对2015 年1 月到2019 年12 月上海市东方医院呼吸内科住院量的时序数据进行建模，然后利用粒子群算法（PSO）算法求出两种模型对应的组合系数，从而得到最终的Prophet-LSTM-PSO 组合模型，并与单个预测模型Prophet，LSTM，ARIMA 模型的预测结果进行比较。结果表明，在医院住院量时序数据预测中，本文提出的组合模型Prophet-LSTM-PSO 的预测效果优于单个模型的预测效果，预测性能更佳。

1 研究理论与方法

1.1 基于医院住院量的LSTM 模型

LSTM 是循环神经网络（RNN）的一种特殊形式，通过遗忘门、输入门和输出门3 个“门”控制信息量的传入，并通过引入“记忆细胞状态”对其进行长期保存。LSTM 单元结构如图1 所示。

图1 LSTM 单元Fig.1 LSTM unit

在医院呼吸内科住院量的时序数据预测中，ft为遗忘门的控制函数，通过输出0～1 之间的数用于对上一时刻的呼吸内科住院量向量数据进行选择。ht为当前时刻的呼吸内科住院量转换向量，xt为 当前时刻的呼吸内科住院量向量， [ht-1,xt]是2 个向量连接的长向量。Yt为t时刻呼吸内科住院量的输出向量。t为当前时刻，t-1为上一时刻。W为各层对应的权重矩阵，b为偏差向量，下标f，i，o分别代表遗忘门、输入门和控制门。

it为输入门的控制函数，与ft类似，通过改变权重矩阵的值对新输入的呼吸内科住院量数据进行选择，以避免相关性较低的呼吸内科住院量值加入记忆细胞。是当前时刻真实的呼吸内科住院量的tanh 函数转换值，作为当前时刻呼吸内科住院量的信息向量。

当前时刻记忆细胞的存储向量Ct用于对当前时刻呼吸内科住院量向量进行选取、转换、存储，Ct是将上一时刻的存储向量和当前时刻新输入的呼吸内科住院量的信息向量分别与遗忘门控制函数向量、输入门控制函数向量进行逐元素相乘，进而实现对较长时间的呼吸内科住院量相关信息量的记忆存储。

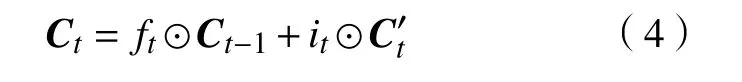
ot为输出门的控制函数，用于对当前时刻呼吸内科住院量预测向量的输出控制。

为经转换之后的呼吸内科住院量预测值，minJ(θ)代表LSTM 的损失函数。

式中：Wy为输出门上一时刻呼吸内科住院量的存储值权重矩阵；Lt为呼吸内科住院量实际值。

LSTM 模型通过采用损失函数对输出值的倒数作为误差项随时间进行反向传播，该算法称为基于时间的反向传播算法（BPTT），其基本思想主要分为4 个步骤：

步骤1运用式（1）～（7）前向计算出各个神经元的输出值ft，it，Ct，ot，ht，L¯t；

步骤2从时间和网络层级2 个方向反向计算每个神经元的损失函数对其输出值的倒数，即每个神经元的误差项；

步骤3根据每个神经元的误差项值对其相应的权重计算梯度；

步骤4运用梯度下降法更新权重矩阵和偏差向量。

1.2 基于医院住院量的Prophet 模型

在使用LSTM 对原始数据进行预测的同时，采用Prophet 模型进行预测。

2017 年Facebook 发布了Prophet 时序先知模型，主要研究时序数据的特征和时序变化规律，同时预测未来的走势。Prophet 的核心是分析包含周期性、趋势性以及节假日效应等的时间序列特征，它是一种针对时序的有效集成解决方案，Prophet模型的构成为

式中：g(t)为趋势函数，用来分析时间序列中的非周期性的变化；s(t)代表周期性的变化，例如，一年或一周的周期性；h(t)代表节假日等偶然一天或几天造成的影响； ε为随机波动，代表模型没有考虑到的误差的影响[5]。

a.趋势项。Facebook 采用改进的Logistic 增长模型，其中，饱和值是随时间动态变化的，而且增长率也会随着新产品等因素发生变化。

式中：C(t)为随时间变化的饱和值（承载能力）；k+a(t)Tδ 为随时间变化的增长率，为相应的偏置参数；S j为 若干个转折点； δ为转折点处增长率的变化量。

b.周期项。Prophet 模型依靠傅里叶级数来构造灵活的周期性模型，基本形式为

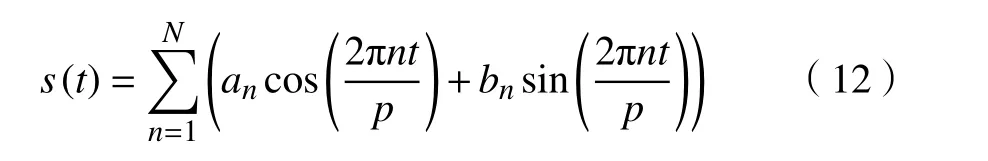
式中：p为时间序列的周期长度；N为周期数；an，bn为需要估计的参数。

1.3 基于医院住院量的PSO 模型

在多元回归中，求解回归参数的常用方法有最小二乘法、梯度下降法及牛顿法等，但是，这些方法涉及大量的矩阵计算，且计算速度较慢。而PSO 算法最初是基于自然界中存在的鸟类捕食活动现象所产生的智能模拟算法，该算法相较于遗传算法（GA）、蚁群算法（ACO）等具有简单高效、参数少及收敛速度快等特点。因此，本文借助粒子群算法确定组合模型的权重系数。

PSO 算 法 将回归 系数组合 (α, β)看 成一个 粒子，随机初始化多个粒子，每个粒子通过位置和速度更新方程，向最优解“靠拢”。

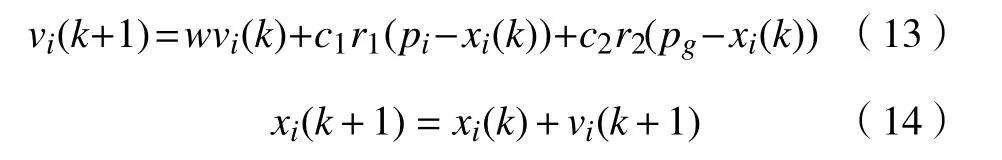
式中：vi(k)，xi(k)分 别为粒子的速度和位置；c1，c2分 别为粒子移动到该粒子历史最优位置pi和当前所 有 粒 子 最 优 位 置pg的 加 速 项 因 子；r1，r2为0-1 之间的随机因子；w为惯性因子，是粒子之前运动方向在当前运动方向上的惯性。

最后，通过定义适应度函数

2 Prophet-LSTM-PSO 模型构建与预测

2.1 数据概况及预处理

为了验证模型的可行性与有效性，选取了上海市东方医院（本院及南院）呼吸内科2015 年1 月到2019 年12 月这60 个月住院量数据为研究对象。将数据中存在的缺失值，运用历史同期和近3 期数据的平均值进行填充，获得完整的原始输入数据。对原始输入数据，首先将其转换为与模型输入维度相同的类型，然后将转换后的数据集分为两类，其中，80%的数据即从2015 年1 月到2018 年12 月的96 个数据（本院48 个，南院48 个）用于训练模型，剩余的2019 年1 月至2019 年12 月的24 个（本院12 个，南院12 个）数据作为测试集，用于对模型拟合效果进行验证。

2.2 Prophet-LSTM-PSO 组合模型构建

时间序列数据中蕴含着大量不确定信息，应用单一模型的预测效果往往不是很理想。因此，为了提高预测的准确率，将LSTM 和Prophet 两种模型进行组合，应用PSO 算法求解两种模型的组合系数以提高求解速度，充分发挥组合模型的优势。

基于LSTM 和Prophet 组合模型的建模步骤：

步骤1对数据中缺失的小部分数据，结合近3 个月数据趋势和每一年同期数据，采用平均法进行填充；

步骤2对经过步骤1 处理的原始数据进行归一化处理，使得训练数据的极差尽可能小。然后运用式（1）～（8）对时间序列 {Xt}进行训练和预测，得到LSTM 模型的预测值L¯t；

步骤3对经过步骤1 处理的原始数据进行log 处理，使其尽量符合正态分布。然后运用式（9）～（12）对时间序列 {Xt}进行训练和预测，得到Prophet模型的预测值

步骤4通过构建适应度函数Q(θ)，使得组合模型预测值尽可能逼近真实值，并采用PSO 算法对组合模型的系数 α和 β进行求解；

步骤5组合两种模型的预测结果，获得组合模型预测值

2.3 Prophet-LSTM-PSO 组合模型训练

2.3.1 LSTM 模型训练参数

在Python 3.6 软件的基础上，将LSTM 模型分别应用于训练集和测试集，获得单一模型下的各种具体参数，其中，输入向量为（2，1）的维度的时序数据，输入层神经元数为8，隐藏层为1 层，神经元数为128，隐藏层激活函数为RELU 函数，即为f(x)=max(0,x)，输出层神经元数为1。本实验中训练数据“轮”次数为100，采用随机梯度下降算法。

2.3.2 Prophet 模型训练参数

在Python 3.6 软件的基础上，将Prophet 模型分别应用于log 处理后的数据集，获得单一模型下的各种具体参数，输入向量为（2，60）的时序数据，趋势项为改进的Logistic 增长模型，周期项取傅里叶级数，拟合函数为Fit 函数。

2.3.3 组合模型训练与结果分析

将两种单一模型的预测结果进行组合，并应用PSO 算法求解组合模型的系数α和β，从而获得组合模型的预测值。

本院的组合预测模型为

南院的组合预测模型为

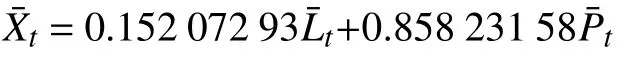
3 实验结果与分析

将组合模型与常用的单一模型（Prophet，LSTM，ARIMA 模型）在相同的测试集进行定量分析，结果表明，LSTM-Prophet-PSO 组合模型的预测结果较单一模型要好，预测值与实际值的误差值较小，为了更加直观地观察预测结果，将上海市东方医院（本院）住院量的4 种模型实际值与预测值进行可视化，如图2 所示。从图2 中可以看出，组合模型拟合效果最好，其次是Prophet 模型，再次是ARIMA 模型，最后是LSTM 模型。与其他几种单一模型相比，组合模型在训练集和测试集上都有较好的拟合效果，符合时序数据的大致趋势。

为了对模型的效果进行科学的评估，分别计算了各个模型的整体均方根误差（RMSE）和平均绝对误差（MAE），并将LSTM-Prophet-PSO 组合模型与Prophet，LSTM，ARIMA 模型进行对比，以验证该方法的可行性与有效性。不同模型在相同指标下的对比结果如表1 所示。

为了增加本文的可信度，采用公开数据集，即我国新型冠状病毒肺炎疫情的累计确诊量的时序数据进行对比实验，实验数据为2020 年1 月24 日到2020 年4 月19 日我国累计确诊人数，应用本文所建立的模型，得到组合模型为=-0.064 883 51+1.064 045 72，并分别计算LSTMProphet-PSO 组合模型与Prophet，LSTM，ARIMA模型的RMSE 和MAE，如表2 所示。

从表1 和表2 可以看出，组合模型与其他3 种单一模型相比，预测精度最高，其相对于Prophet，LSTM，ARIMA 这3 种单一模型在RMSE 和MAE上都有明显的提高。

图2 模型的实际值与预测值对比Fig.2 Comparison of actual and predicted values of the model

表1 实验组：不同模型的整体均方根误差与平均绝对误差对比Tab.1 Trial group: comparison of RMSE and MAE of different models

表2 对比实验组：不同模型的整体均方根误差与平均绝对误差对比Tab.2 Control group: comparison of RMSE and MAE of different models

4 结束语

通过分析医院住院量的时序数据的特征与趋势，进一步分析医院住院量预测的准确度，对于医院及时调整医院资源配置具有重要的参考意义。根据上海市东方医院呼吸内科住院量时序数据的规律，提出了一种基于Prophet 模型和长短期记忆网络（LSTM）的组合模型预测方法，通过粒子群算法确定组合模型中的权重系数，并与Prophet，LSTM，ARIMA 模型这3 种单一模型的预测效果进行对比。利用公开数据集，即我国新型冠状病毒肺炎疫情的累计确诊量的时序数据进行对比实验。实验结果表明，通过PSO 计算得出的组合模型的预测性能优于单个Prophet，LSTM，ARIMA模型的预测性能。本文对医院住院量的研究只考虑了历史数据的影响，在进一步预测时可考虑多个影响因素，例如，气温、湿度等因素对呼吸内科住院量的影响[6-9]。