水稻流行性病虫害传播系统的渐近解
2021-03-15汪维刚汪维莲汪方圆
汪维刚,汪维莲,汪方圆
(1.安徽师范大学 数学和计算机科学学院,安徽 芜湖 241003;2.芜湖职业技术学院 应用外语学院,安徽 芜湖 241000;3.合肥幼儿师范高等专科学校 公共教学部,安徽 合肥 230011;4.云南大学 软件学院, 云南 昆明,650091)
0 引 言
当前农药滥用现象普遍,食品中毒、地表水污染、肺癌发病与死亡等变化率在上升,让人感到可怕的是不少农民竟然还没有意识到其巨大危害性.为了在理论和实践双层面上解决农药适量使用问题,极大可能地将农药对土壤、水稻等的毒副作用降低到最低程度,同时降低农业生产成本,当前迫在眉睫的任务是研究水稻流行性病虫害传播系统的渐近性。文献[1-5]主要研究了针对病虫害的不同类型在水稻生长的不同阶段所采用的不同方法,有物理防治方法、生物防治方法、农业防治法和化学防治方法;文献[6-7]研究了喷洒农药主要集中在水稻害虫虫卵的高发阶段,并采取了循序渐进的方式喷洒,而不是批量消灭害虫,避免了病虫卵产生抗药体;文献[8-40]研究了农药对不同类型的病虫害使用策略及效用等;而且文献[5-6,8-40]都不同程度地指出了过于依赖化学农药的投入,以及化学农药使用的不合理,都必将造成环境污染,破坏生态环境.
1 水稻流行性病虫害传播系统
1.1 流行性病虫害传播动力学系统模型
考虑如下水稻流行性病虫害传播的生态动力学的系统模型:
(1.1)
(1.2)
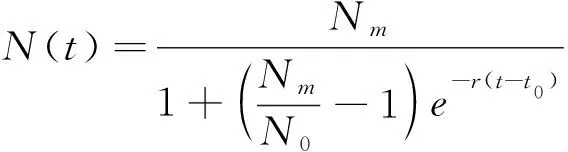
(1.3)
其中u(t)和v(t)分别表示在水稻流行性病虫害传播区域内的感染者株数和易感者株数,t为时间变量,d≥0表示易感者出生率,a,a1,b,b1,c,c1均为常数.在生态动力学系统(1.1),(1.2)中,auv表示由感染者与易感者因“交感”而造成的水稻被侵害增加速度,-buv2表示由采取防疫和治疗措施后使得水稻被侵害减少的速度,af1(u)表示由于水稻死亡而引起的水稻被侵害减少速度,-a1uv项表示感染者与易感者“交感”易感者变为感染者后使得易感者所减少的速度,-b1u2v项表示采取防疫和治疗措施后使得易感者所减少的速度,c1u项表示感染者增多时易感者的增加速度,a1f2(v)表示其他因素的影响。系统(1.1),(1.2)是一个典型的在患区水稻的流行性病虫害传播的生态动力学系统模型。由于(1.1),(1.2)是非线性动力学系统,它一般不能得到系统的初等函数的精确解,故求动力学系统(1.1),(1.2)解的渐近表达式,从将得到的表示式来定性地研究水稻流行性病虫害的传播形态和规律,其中N(t)为农药需求函数,Nt=0=N0,Nm为水稻生长环境对农药使用的最大容量,r为参数,t为时间。
1.2 变分迭代
从Eqs.(1.1),(1.2)可构建如下泛函:
(1.4)
(1.5)
令δFi=0,i=1,2.得到
因此,
λ1=exp(β(t-τ)),β=bv2,λ2=1
(1.6)
从 Eqs.(1.6),(1.4) 和 (1.5),我们构建下列泛函变分迭代式
(1.7)
(1.8)
我们选取如下零次迭代解
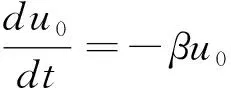
(1.9)
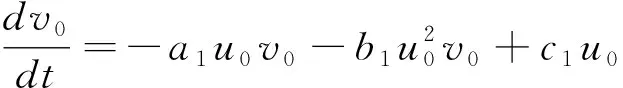
(1.10)
u0|t=0=u(0),v0|t=0=v(0)
(1.11)
其中u(0),v(0)是初始值 ,得到线性问题 (1.9)-(1.11)的解
u0(t)=u(0)exp(-βt)
(1.12)
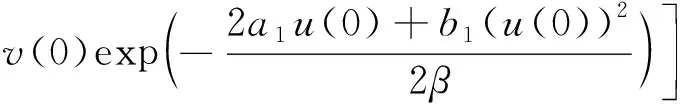
(1.13)
用零次近似解(1.12)和 (1.13) 替代广义泛函变分迭代式(1.7)和(1.8),我们能得到此模型(1.1),(1.2)的一次近似解:
0 (1.14) (1.15) 这里 (1.16) (1.17) (1.18) 0 (1.19) (1.20) 为了使用泛函映射方法得到水稻流行性病虫害传播的生态动力学系统的模型(1.1),(1.2)的渐近解,令 (1.21) 其中p∈[0,1]为人工参数[47,48].现引入一组泛函分析同伦映射Hi(u,v,p),R2×I→R,i=1,2: H1(u,v,p)=L1(u,v)-L1(u0,v0)+p[L1(u0,v0)-auv+buv2-af1(u)] (1.22) H2(u,v,p)=L2(u,v)-L2(u0,v0)+p[L2(u0,v0)+a1uv+b1u2v-c1u-a1f2(v)] (1.23) 其中I=[0,1],R=(-∞,+∞),(u0,v0)为水稻流行性病虫害传播的生态动力学系统(1.1),(1.2)的初始的函数,线性算子 为 (1.24) (1.25) 显然,由(1.22)-(1.25)式知,Hi(u,v,1)=0(i=1,2)是水稻流行性病虫害传播的生态动力学系统(1.1),(1.2).故系统(1.1),(1.2)的解(u(t),v(t))就是系统Hi(u,v,p)=0的解当p→1的极限. (1.26) (1.27) 且由(1.26),(1.27)式,初始值为u(0)=A1,v(0)=A2的解,不难可得到: (1.28) (1.29) 将(1.21)式代入(1.22),(1.23)式,展开非线性项关于p的幂级数,比较等式两边p的同次幂项的系数。由p的零次幂的系数可得 (1.30) U0(t)=u0(t)=A1exp(-ct) (1.31) (1.32) 由动力学模型(1.1),(1.2)解的零次近似(1.31),(1.32)及泛函分析同伦映射(1.22),(1.23)可得: (1.33) (1.34) 其中u0,v0分别为(1.31),(1.32),不难看出,系统(1.33),(1.34)且在零初始条件(u1(0),v1(0))=(0,0)下的解为 (1.35) (1.36) 由(1.21),(1.31),(1.32),(1.35),(1.36)式知,令p=1,水稻流行性病虫害传播的生态动力学系统(1.1),(1.2)的一次函数(U1,V1)是: (1.37) (1.38) 由动力学系统模型(1.1),(1.2)解的零次近似(1.31),(1.32)及(1.35),(1.36)式和泛函分析同伦映射(1.22),(1.23)可得: (1.39) (1.40) 其中ui,vi(i=1,2)分别为(1.31),(1.32),(1.35),(1.36).不难看出,动力学系统(1.39),(1.40)且在零初始条件(u2(0),v2(0))=(0,0)下的解为 (1.41) (1.42) 同样可得水稻流行性病虫害传播的生态动力学系统(1.1),(1.2)解的n次函数(Un,Vn)(n=3,4,…)。 在物理防治、生物防治、农业防治等方法综合使用的基础上,研究了水稻流行性病虫害传播规律,使用药量在多因素综合影响下确保毒副作用小、水稻安全生产、生产成本小等目标得以实现,在文献[41-43]的启发下建立了数学模型,并用变分迭代、同伦映射等方法求出了水稻流行性病虫害传播的生态动力学系统的渐近解,真正实现科学地使用农药,从而造福人类.
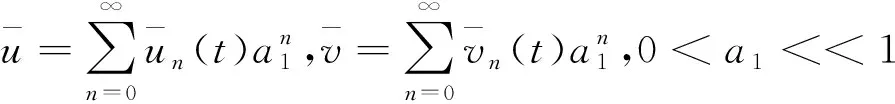

1.3 泛函分析同伦映射
2 动力学模型渐近解
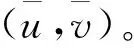

3 结语
