考虑媒体影响的一类时滞传染病模型的分岔周期解

张子振, 张怡雪, 张伟诗, 宋志强

( 1.安徽财经大学 管理科学与工程学院, 安徽 蚌埠 233030;2.呼伦贝尔学院 工学院, 内蒙古 呼伦贝尔 021008 )

0 引言

传染病是严重威胁人类健康和生命的一类疾病.研究显示,在传染病暴发期间,网络、电视等媒体对疾病的暴发情况进行客观准确的宣传报道,可以使公众准确了解疾病的传播情况和提高对传染病的防范意识,从而有助于控制疾病的传播[1-2];因此,近年来考虑媒体影响的传染病模型受到学者们的关注.例如:李录苹等[3]提出了一类考虑媒体报道效应的SEIQR传染病模型,并通过构造合适的李雅普诺夫函数研究了无疾病平衡点的全局渐近稳定性.张雪妮等[4]研究了一类受媒体报道影响的离散传染病模型,并分析了无疾病平衡点和有疾病平衡点的稳定性.张钰倩等[5]和阳丽君等[6]考虑到媒体宣传的滞后性,分别研究了不同类型的时滞传染病模型,并针对其模型推导出了模型产生Hopf分岔的充分条件;但是,张钰倩等和阳丽君等并未对其模型的Hopf分岔的性质进行研究.刘中凯等[7]建立了一类同时考虑媒体影响和疫苗接种影响的传染病模型:

(1)

其中:Sn(t)、Sa(t)、I(t)和V(t)分别表示无意识易感者、有意识易感者、感染者和接种者在时刻t的数量,M(t)表示媒体在时刻t的报道信息量;A为无意识易感者的常数输入率;λ为无意识易感者向有意识易感者转化的比率;β0为无意识易感者的感染率;λ0为有意识易感者向无意识易感者转化的比率;r为感染者的恢复率;p和q分别为感染者恢复后转化为无意识易感者的比率和感染者恢复后转化为有意识易感者的比率,p+q= 1;ω为接种者失去免疫力的比率;f和δ分别为接种者失去免疫力后转化为无意识易感者的比率和接种者失去免疫力后转化为有意识易感者的比率,f+δ= 1;θ为有意识易感者的接种率;a为感染者因疾病导致的死亡率;d为所有群体的自然死亡率;μ为媒体对疾病进行宣传的力度;μ0为媒体在宣传过程中的信息耗散率.在文献[7]中,刘中凯等研究了模型(1)的稳定性,并通过数值模拟分析了公众意识和疫苗接种率对疾病传播的影响,但其研究未考虑媒体宣传的滞后性.基于上述研究,本文研究如下时滞传染病模型:

其中:ζ表示媒体对疾病进行宣传报道的滞后时间.

1 局部稳定性和Hopf分岔的存在性

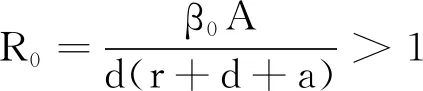
(3)

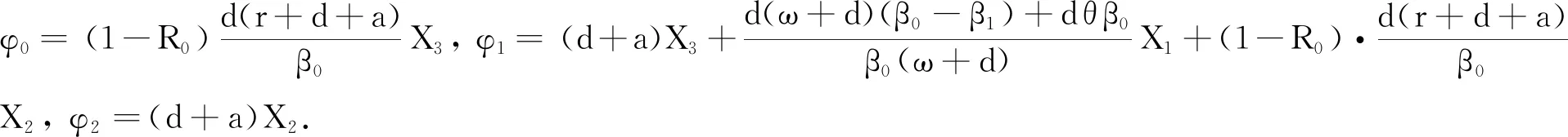
模型(2)在有疾病平衡点D*(Sn*,Sa*,I*,V*,M*)处的雅克比矩阵为:

其中:k11=-λM*-β0I*-d,k12=λ0,k13=-β0Sn*+rp,k14=ωf,k15=-λSn*,k21=λM*,k22=-λ0-β1I*-θ-d,k23=-β1Sa*+rp,k24=ωδ,k25=λSn*,k31=β0I*,k32=β1I*,k33=β0Sn*+β1Sa*-r-a-d,k42=θ,k44=-ω-d,k55=-μ0.

模型(2)在有疾病平衡点处D*(Sn*,Sa*,I*,V*,M*)的特征方程为:

ρ5+Θ4ρ4+Θ3ρ3+Θ2ρ2+Θ1ρ+Θ0+(Ξ2ρ2+Ξ1ρ+Ξ0)e-ρζ= 0.

(4)

其中:

Ξ0=-μ[(k15(k22k31k44-k24k31k42-k21k32k44)+k25(k11k32k44-k12k31k44+k14k31k42)],

Ξ1=-μ(k15k21k32-k15k22k31-k15k31k44-k25k32k44-k11k25k32+k12k25k31),

Ξ2=-μ(k15k31+k2k32),

Θ0=k44k55(k11k23k32+k12k21k33+k13k22k31-k11k22k33-k13k21k32-k12k23k31)+

k42k55(k11k24k33+k14k23k31-k14k21k33-k13k24k31),

Θ1=k44(k11k22k33+k13k21k32+k12k23k31-k11k23k32-k12k21k33-k13k22k31)-

k55[k11k23k32+k12k21k33+k13k22k31-k11k22k33-k13k21k32-k12k23k31-

k44(k11k22+k11k33+k22k33-k23k32-k12k21-k13k31)]-

k42[k11k24k33-k14k21k33-k13k24k31+k14k23k31-k55(k14k21-k11k24-k33k24)],

Θ2=k11k23k32+k12k21k33+k13k22k31-k11k22k33-k13k21k32-k12k23k31+

k44(k12k21+k13k31+k23k32-k11k22-k11k33-k22k33)-k55[k11k22+k11k33+k22k33-

k23k32-k12k21-k13k31+k44(k11+k22+k33)]-k14k21k42+k24k42(k11+k33+k55),

Θ3=k11(k22+k33)+k44(k11+k22+k33)+k55(k11+k22+k33+k44)+k22k33-

k12k21-k13k31-k23k32-k24k42,

Θ4=-(k11+k22+k33+k44+k55).

由上述特征方程可知,当ζ= 0时,方程(4)变为:

ρ5+Δ4ρ4+Δ3ρ3+Δ2ρ2+Δ1ρ+Δ0= 0.

(5)

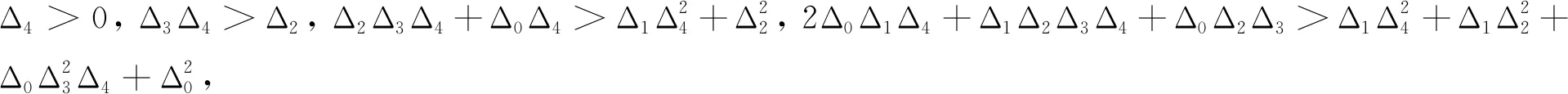
(6)

由式(6)可得:

χ10+α4χ8+α3χ6+α2χ4+α1χ2+α0= 0.

(7)

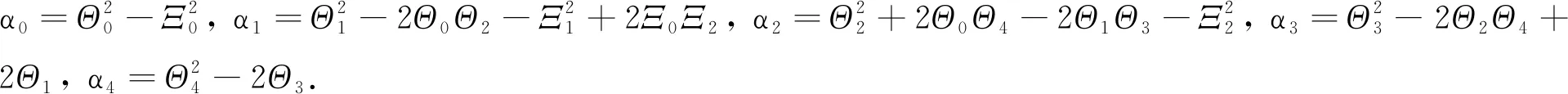
ε5+α4ε4+α3ε3+α2ε2+α1ε+α0= 0.

(8)

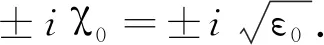
2 分岔周期解的稳定性

令ζ=ζ0+l,l∈R,v1(t)=Sn(t)-Sn*,v2(t)=Sa(t)-Sa*,v3(t)=I(t)-I*,v4(t)=V(t)-V*,v5(t)=M(t)-M*,并对t作变换t→(t/ζ),由此模型(2)可以转换为:

(9)

其中:

Yl(φ)=(ζ0+l)K1φ(0)+(ζ0+l)K2φ(-1),

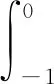
(10)

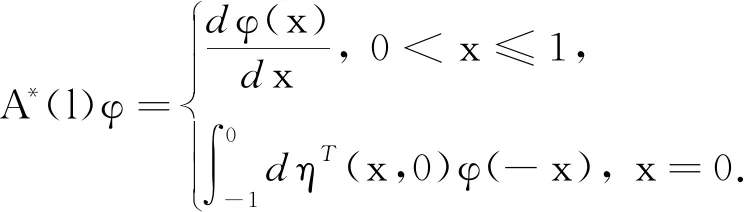
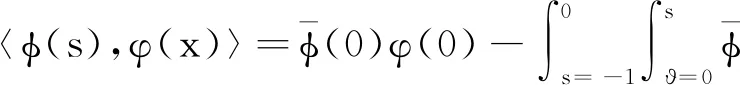
(11)

根据上述计算,再利用文献[8]中的方法即可求得中心流形系数v20、v11、v02和v21的表达式,由此再进一步计算即可得模型(2)在ζ=ζ0处的分岔周期解的稳定性系数:

定理2当Q1>0(Q1<0)时,模型(2)在ζ=ζ0处产生的Hopf分岔是超临界(次临界)的;当Q2>0(Q2<0)时,模型(2)在有疾病平衡点D*(Sn*,Sa*,I*,V*,M*)处产生的分岔周期解是不稳定的(稳定的).

3 数值模拟

模拟参数选取A=2,λ= 0.9,β0= 0.06,λ0= 0.05,r= 0.08,p= 0.8,q= 0.2,ω= 0.15,f= 0.8,δ= 0.2,d= 0.128,β1= 0.03,θ= 0.9,a= 0.001,μ= 0.3,μ0= 0.1.在上述参数下模型(2)变为:

(12)

对式(12)进行计算可知,基本再生数R0=4.4856>1,由此得模型(12)存在唯一有疾病平衡点D*(1.9368,3.0930,0.5878,10.0133,1.7634),且χ0= 0.9057,ζ0= 13.0471.为了验证模型(12)Hopf分岔的存在性,本文首先选取ζ=12.0675∈[0,ζ0).此时,模型(12)的状态图和相图分别如图1和图2所示.由图1和图2可以看出,模型(12)是局部渐近稳定的.其次,选取ζ=15.2625>ζ0.此时,模型(12)的状态图和相图分别如图3和图4所示.由图3和图4可以看出,此时模型(12)失去稳定性,并在有疾病平衡点D*(1.9368,3.0930,0.5878,10.0133,1.7634)附近产生了Hopf分岔.

图1 ζ=12.0675∈[0,ζ0)时模型(12)的状态图

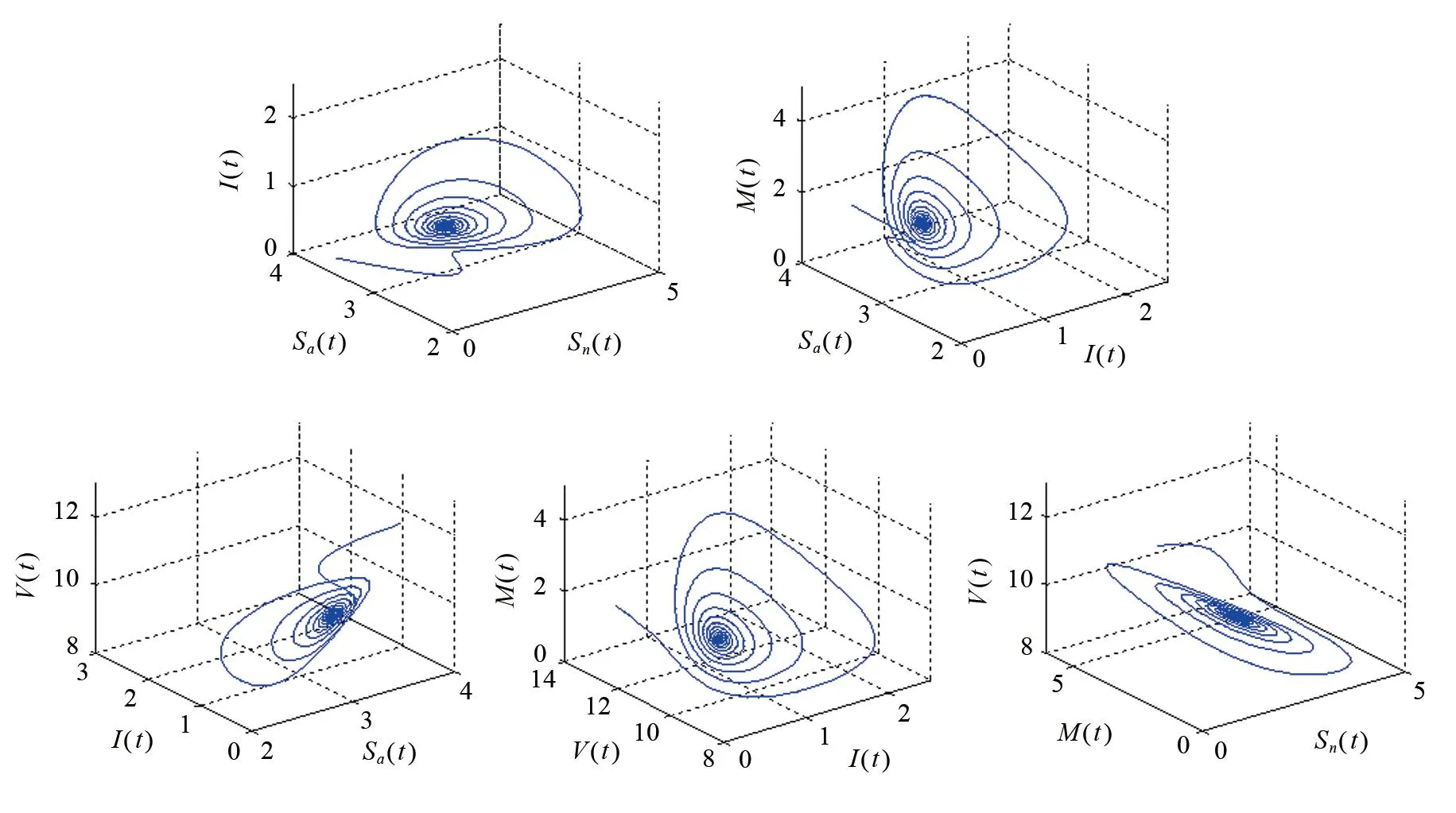
图2 ζ=12.0675∈[0,ζ0)时模型(12)的相图

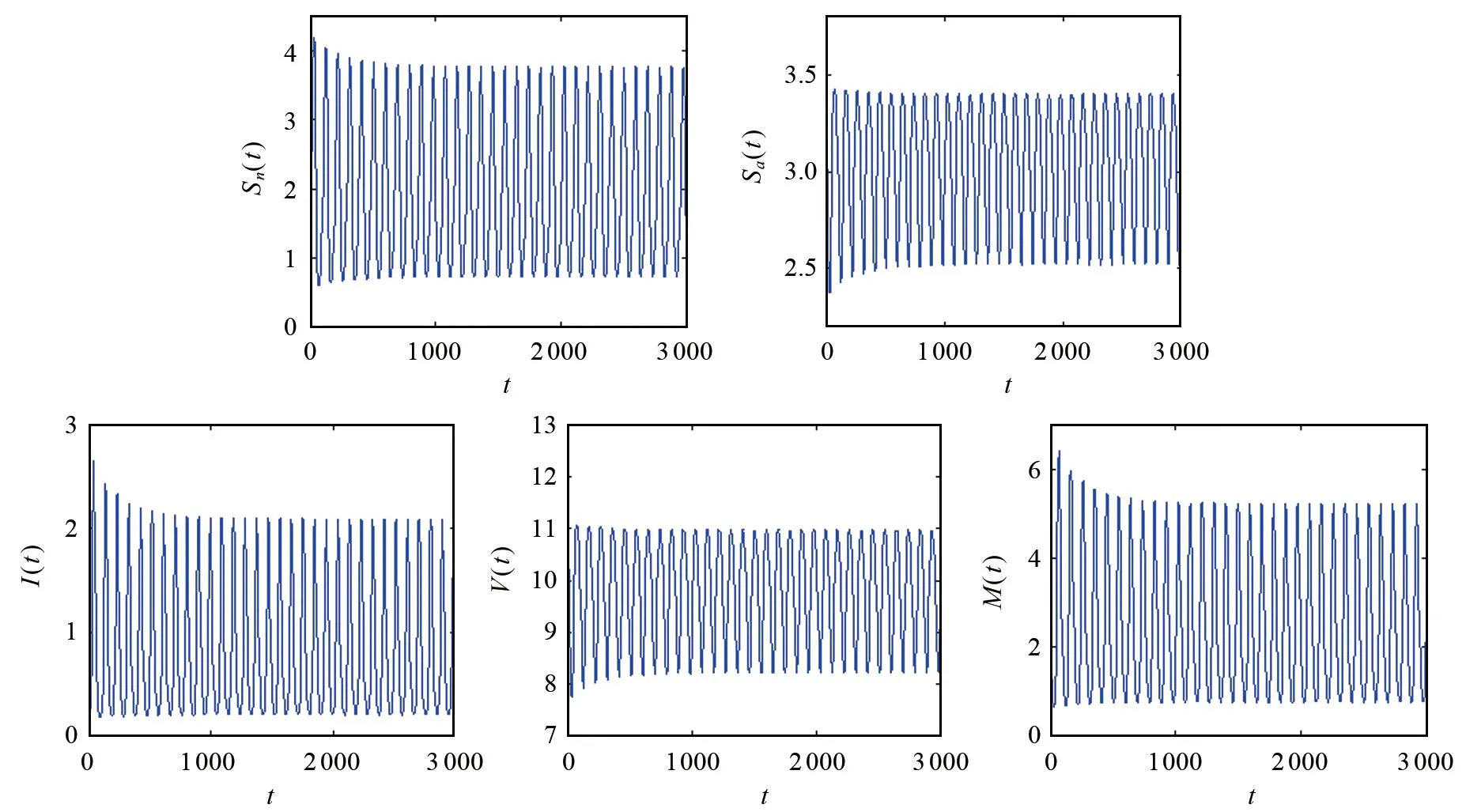
图3 ζ=15.2625>ζ0时模型(12)的状态图

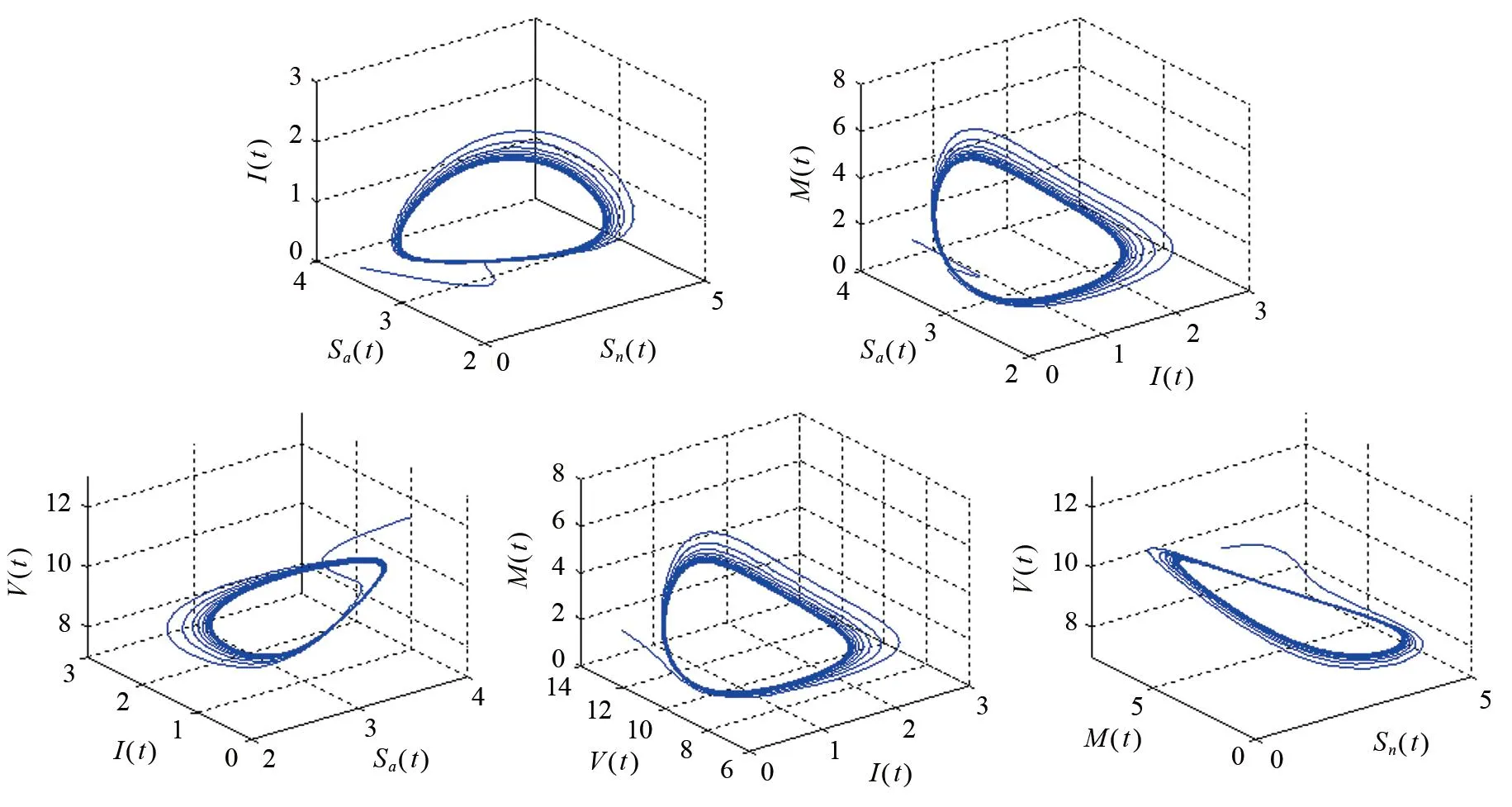
图4 ζ=15.2625>ζ0时模型(12)的相图

4 结论

本文研究表明:当媒体对疾病进行宣传报道的滞后时间足够短时,模型(2)中的无意识易感者、有意识易感者、感染者和接种者的数量将趋于稳定;而当媒体对疾病进行宣传报道的滞后时间超过时滞临界点ζ0时,模型(2)中的无意识易感者、有意识易感者、感染者和接种者的数量将在有疾病平衡点处产生周期震荡.由此表明,媒体对疾病进行宣传报道的滞后时间对模型(2)稳定性具有非常重要的影响.同时也说明,在疾病暴发前,若媒体在客观条件允许的前提下能及时地对疾病进行宣传报道,则有助于控制疾病的传播.本文在研究模型(2)的Hopf分岔时,仅研究了其局部Hopf分岔行为;因此,在今后的研究中我们将研究模型(2)是否存在全局Hopf分岔行为.