基于索力响应面法的斜拉桥模型修正

李延强，刘晓慧，陈泽林，张 浩

(石家庄铁道大学 工程力学系， 河北 石家庄 050043)

桥梁作为交通工程的枢纽，在我国的经济建设中承担着重要的作用，其服役性能和结构安全受到工程界和学术界的高度重视。桥梁的力学性能分析以及状态评估常基于结构设计图纸而建立的有限元模型展开，但在建模过程中往往需要进行理想简化和假设，因此分析结果与实际情况存在一定的偏差。有限元模型修正是减小此类误差的有效手段之一[1-4]。诸如斜拉桥这类大跨度桥梁进行性能分析与安全评估是，更需要一个能同时较好的反映结构整体和局部受力的计算模型，因此基于多尺度的有限元模型及其修正技术被越来越多的用于大跨桥梁的力学行为分析及损伤评估研究[5-9]。

基于响应面的有限元模型修正技术相比于传统的模型修正方法具有计算工作量小，修正效率和精度高的特点，近年来在土木工程领域得到越来越广泛的应用。任伟新等[10]提出了一种回归分析法和实验设计与响应面相结合的桥梁有限元模型修正方法。宗周红等[11]将结构的健康监测与响应面模型修正相结合，成功对白石大桥支座进行了损伤识别。张伟杰等[12]提出一种逆响应面修正方法，可直接得到设计参数的修正量，并通过一座简支梁桥进行了数值验证。郁胜等[13]将基于径向基函数的响应面模型与遗传算法相结合，实现了某超大跨钢桁架悬索桥的模型修正。

综上所述，基于响应面的桥梁多尺度模型修正技术研究文献资料较少，针对斜拉桥开展的多尺度建模与响应面修正的研究更鲜有报道。因此，本文首先采用多点约束法建立斜拉桥的一致多尺度分析模型，然后基于多项式函数建立索力响应面方程，在此基础上，开展基于斜拉索索力响应面的斜拉桥模型修正方法研究，并通过实测索力值与数值仿真索力值的对比分析，验证了该方法的有效性和可靠性。

1 斜拉桥一致多尺度建模

1.1 一致多尺度模型

采用不同尺度的不同单元模拟桥梁不同部位，通过合理连接方式连接而成的有限元模型称为桥梁一致多尺度模型。针对斜拉桥，建模步骤如下：

(1)首先采用壳单元或梁单元(单元特征长度为101m级)，忽略桥梁局部的构造细节，建立桥梁整体大尺度模型。通过有限元计算，确定斜拉桥的重点部位(关键截面和危险构件等)。

(2)采用实体单元(单元特征长度为10-3m级)，按照整体模型对应坐标位置，建立桥梁重点部位的局部小尺度模型。

(3)删除整体模型中与局部模型对应位置的单元，删除的单元应与局部模型的大小、形状、坐标等完全相同。

(4)通过多点约束法将小尺度局部模型与大尺度整体模型边界连接，形成一致多尺度模型，实现大、小尺度模型的协同工作。

1.2 多点约束法

多点约束法定义的是不同单元连接处节点(主从节点)自由度的耦合关系，即建立主从节点的位移约束方程，实现有限元模型中不同单元界面的连接。以实体单元与壳单元为例，两种不同尺度单元间的连接如图1所示。

根据主从节点的位移协调关系，建立节点位移约束方程为

ui=u1-yi·φw1

(1)

vi=v1+xi·φw1

(2)

wi=w1+yi·φu1-xi·φv1

(3)

式中：ui、vi、wi表示从节点坐标轴方向的线位移；u1、v1、w1为主节点的线位移；φu1、φv1、φw1分别为主节点绕x、y、z轴的转角位移。

2 基于索力响应面的模型修正方法

首先选择斜拉桥合适的设计参数(材料参数和几何参数)作为输入响应，以索力作为目标输出，通过中心复合设计方法，选择对斜拉索索力响应显著性好的参数，然后采用二次多项式法进行斜拉索索力响应面方程拟合；最后基于实测索力，运用最小二乘法优化响应面模型，精度校验合格后参数取值即为参数修正值，模型即为最优有限元模型。实现流程如图2所示。

图2 斜拉桥多尺度有限元模型修正流程图

(1)筛选特征量：基于响应面方法中特征量的选择较为广泛，斜拉索索力是衡量斜拉桥受力状态的重要指标，故本文选取斜拉索索力作为目标输出。

(2)筛选参数：选取主梁以及与子模型连接的斜拉索的材料特性作为修正参数，基于响应面分析软件进行计算分析，采用基于方差分析的F检验法筛选对索力响应的著性好的参数作为输入响应。

F检验法主要步骤为：

首先计算索力样本数据中由于试验误差引起的偏差平方和以及各设计变量引起的偏差平方和，分别用SE和SB表示，某参数X的自由度和偏差的自由度分别nB和nE表示，则FX的表达式为

(4)

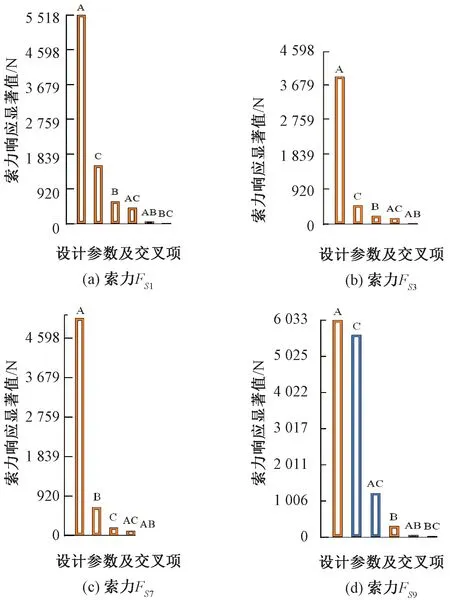
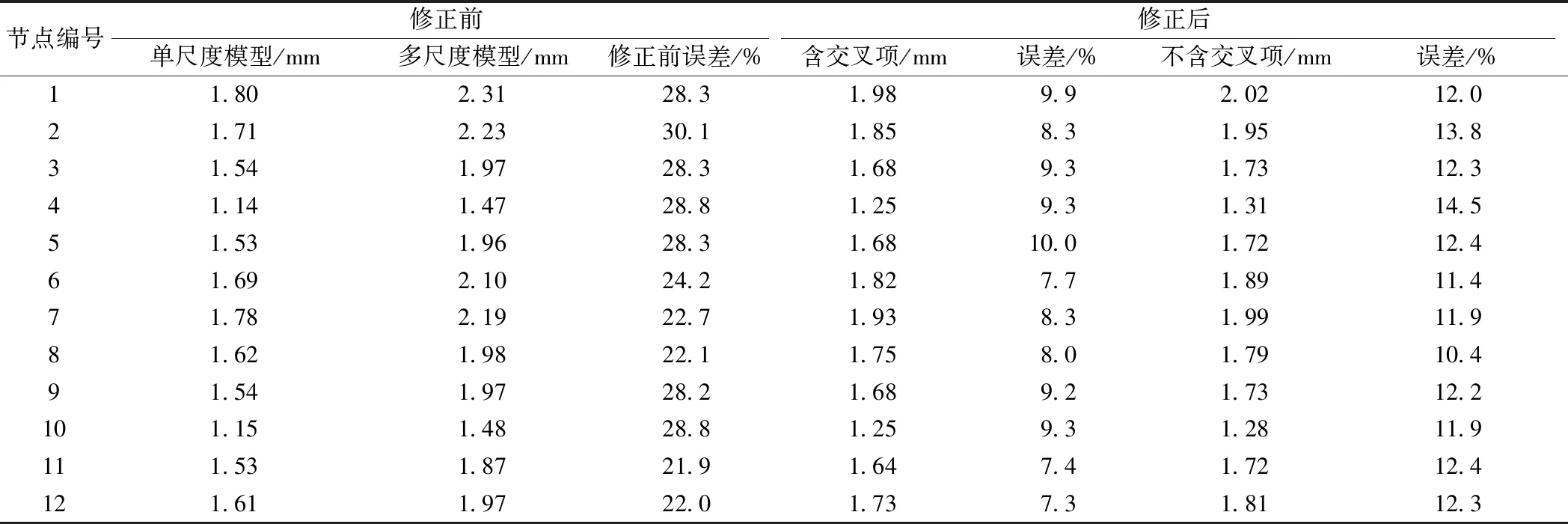
式中：α表示参数的显著性水平。若FX≥F1-0.01(nB,nE)，则称参数X的影响高度显著；若F1-0.01(nB,nE)>FX≥F1-0.05(nB,nE)，则称参数X的影响显著；若F1-0.05(nB,nE)>FX≥F1-0.01(nB,nE)，则称参数X有一定的影响，若FX

(3)响应面拟合：选取显著性较高的一组作为修正参数，适当设定修正参数的上下界，进行试验设计获得不同的修正参数组合。采用有限元方法分析不同组合下的索力响应，进而采用多项式法拟合索力响应面方程，即得到索力响应面模型。

(4)模型优化。将参数的目标值(即实测索力)代入响应面方程，模型精度采用R2准则[14]检验。若满足要求，则进行参数修正；否则重复(3)、(4)，直至满足要求。

3 数值仿真

3.1 多尺度有限元模型

本文以实验室独塔斜拉桥为研究对象，桥梁结构尺寸及模型试验参见文献[15]。采用有限元分析软件Ansys建立一致多尺度有限元模型。模型桥大尺度单元采用Shell63模拟，小尺度单元采用Solid65模拟，斜拉索采用Link10 (只受拉)模拟，见图3。

图3 一致多尺度有限元模型

3.2 实验设计

根据经验，选取主梁弹性模量E及密度ρ、斜拉索横截面积S及泊松比μ作为待修正参数，见表1。且将各参数阈值设定为初始值的±30%。斜拉索编号示意见图4，考虑到响应面方程与斜拉索的空间位置无关，故任选A1、A3、A7、A9等4条斜拉索，将其索力作为目标输出，分别以FS1、FS3、FS7、FS9表示。将选择的修正参数作为设计因子，利用响应面分析软件Design Expert进行实验设计，得到设计矩阵，即待修正参数的不同组合。一共进行16次实验，将这些参数的不同组合带入有限元初始模型进行受力计算，计算得到4条斜拉索的索力。

表1 模型斜拉桥实验参数初始值

图4 斜拉索编号示意

3.3 参数筛选

计算完成后，采用基于方差分析的F检验法分析各参数对斜拉索索力的影响效应，选取影响效应大的参数作为待修正变量，见图5。

图5 参数对各斜拉索索力的影响效应

图5中A、B、C、D分别代表设计参数E、ρ、S、μ对索力响应的效应，AB、AC、BC等代表各参数对索力响应的相互效应，值越大，代表显著性越高，对索力的影响程度也越大。对比分析图5(a)～图5(d)可知，主梁弹模参数E、主梁材料密度参数ρ以及斜拉索截面积参数S的显著性水平较高，表明该三个参数对各索力的影响较为显著。因此选择这三个参数为输入参数，基于响应面法进行参数修正。

3.4 响应面模型

依据参数筛选结果，对选定的参数E、ρ、S进行实验设计，考虑各参数之间的交互作用对索力值的线性影响，采用中心复合设计法经反复试验可得到各索力的响应面模型，见图6，然后按照考虑参数交互影响和不考虑参数交互影响两种情况分别拟合响应面方程，不考虑参数交互影响的响应面方程见式(5)～式(8)；考虑参数交互影响的响应面方程见式(9)～式(12)。

图6 各斜拉索索力的响应面模型

对响应面模型进行精度检验，计算得到的R2值见表2。

表2 索力回归判定系数R2

由表2可知，各样本的R2值均趋近于1，这说明两种情况拟合的响应面模型精度均很高，很好的反应了修正参数与索力之间的关系。

3.5 修正结果

以实测索力为目标值，分计入参数交互影响与不计入交互影响两种情况，依据最小二乘法原理对上述拟合的索力响应面方程修正。修正时各参数的权值均取为1。模型修正后的设计参数取值见表3。

表3 修正前后各设计参数值对比

由表3可知，经过修正，主梁弹模E和主梁材料密度ρ的取值变大，这主要是由于建模时忽略了主梁顶板加劲肋，修正后的结果更加接近实际。同时修正后斜拉索截面面积S减少，这反映了斜拉索在张拉过程中随索力增大，截面面积减小的客观事实。由此可知修正后的参数有效的弥补了一些建模缺陷，具有明确的物理意义。

将斜拉桥模型中的各相关参数设定为表3所示修正值后重新计算，提取斜拉索的索力，并与修正前索力进行对比分析，结果如图7所示。图中，索力实测值采用压力环传感器测量获取。

图7 斜拉桥模型修正前后与实测索力对比

由图7可知，多尺度有限元模型经过修正后索力理论计算值与实测值吻合程度更高，且参数交互作用对索力有一定的影响，修正时宜考虑参数之间的相互作用，即选择考虑交叉项进行修正。

为进一步验证修正效果，对修正前后节点的主应力及竖向位移进行比较。限于篇幅，本文仅给出z=1.5 m处截面节点的第一主应力σ1及竖向位移v的修正前后数值进行比较，节点编号见图8,修正前后σ1见表4。

图8 z=1.5 m处截面节点编号

由表4可知，多尺度模型修正后选取截面处第一主应力偏差明显降低，且含交叉项修正的结果要优于不含交叉项修正的结果。误差较大的8、12号节点，位于底板与腹板交叉位置，该位置受畸变应力影响，应力分布较复杂，加之网格划分时该位置易出现奇异网格，计算近似程度较大，因此造成误差较大。

表4 修正前后σ1值对比

修正前后节点竖向位移v值对比见表5。

表5 节点竖向位移v修正结果

由表5可知，模型经修正后节点竖向位移的计算偏差明显减小，且考虑交互影响的修正偏差小于不考虑交互影响的修正偏差。这是因为z=1.5m截面位于A3索附近，根据前述公式(10)，该索力响应面模型交叉项ES所起作用最大，而E、S参数直接影响结构的刚度，故考虑交叉项时的位移误差小于不考虑交叉项的误差。另外对比模型试验底板中点(对应10号节点)实测位移为1.204 mm，可见修正后的位移更接近实测值，这也一定程度上说明本修正方法可靠。

4 结论

本文在建立斜拉桥多尺度模型的基础上，提出了一种基于索力响应面的有限元模型修正方法，并结合实验室模型桥的实测结果进行了数值验证。结果表明采用该方法修正后的参数物理意义明确，斜拉索索力、主梁截面第一主应力及竖向位移等多个指标的计算偏差明显降低，是一种多目标综合修正方法，且考虑交叉项的修正结果优于不考虑交叉项的修正结果。