基于弹性支承刚度因子的索力计算方法及影响研究
2022-07-13丁继承
丁继承
(长沙理工大公路工程试验检测中心, 湖南 长沙 410014)
0 引言
大跨度桥梁桥型以悬索桥、斜拉桥和中承、下承式拱桥为主。而这些桥型的桥梁均以缆索作为其主要受力构件(悬索桥主索和吊杆、斜拉桥拉索和拱桥吊杆等)。缆索作为整个大跨度桥梁的“生命索”,对缆索桥梁安全运营非常重要。因此,缆索索力的检测对于保障缆索桥梁服役安全十分重要。目前,基于振动法的缆索索力检测方法在桥梁索力无损检测中应用最广[1]。林立等[2]在固支边界条件下,考虑抗弯刚度简化拉索频率方程,该方法在固支边界条件下具有较高精度。李胡生等[3]基于频率分解的方法,建立了铰支边界条件下的缆索拉力计算公式,并分析了固有频率、抗弯刚度和索力之间的关系。而实际的索结构除考虑铰支和固支的情况,还需考虑弹性边界条件的情况。
本文针对弹性边界条件下拉索索力计算问题,基于索结构线性振动理论,考虑弹性支承因子,研究弹性边界下的索力计算方法。通过试验数据对计算方法进行验证,在此基础上探讨了弹性支承刚度因子、抗弯刚度与索力T的关系。
1 拉索频率方程
拉索非齐次边界振动模型如图1所示。先导出该模型的拉索频率方程,并在此基础上对模型的边界条件做不同的简化,得到对应的频率方程。
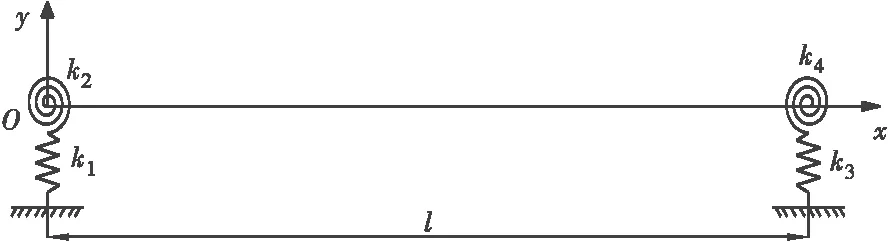
图1 非齐次边界条件下的拉索模型
在图1中,k1~k4为拉索弹性约束的支撑刚度,其中k1、k3对应拉索两端竖向弹性约束,k2、k4对应拉索两端转动弹性约束。该模型的边界条件可以表示为:
(1)
根据拉索线性振动理论,拉索振型方程[2]可以表示为:
Y(x)=Asin(αx)+Bcos(αx)+
Csinh(βx)+Dcosh(βx)
(2)

将式(2)代入(1),可得:
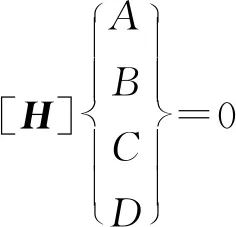
(3)
式中:
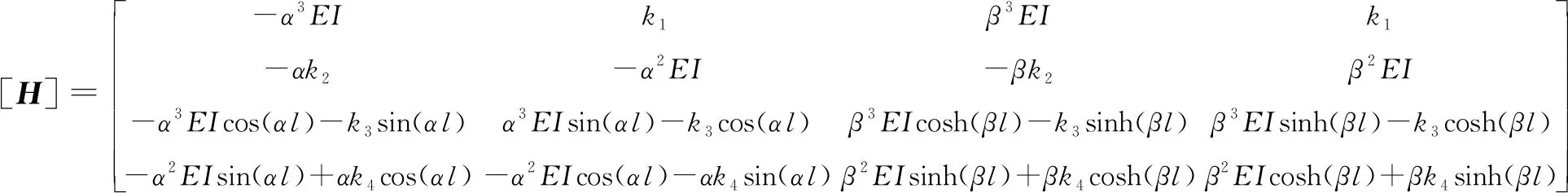
因为式(3)中A、B、C、D不能全为零,因此有:
|H|=0
(4)
实际的索结构除考虑铰支及固支的情况外,有时还需考虑弹性边界条件的情况。原因如下: ①拉索振动时,其锚具端部会承受部分弯矩,起弹性约束作用;②模态实验发现:拉索的振型为铰支与固支耦合形式,索的振动中既有铰支和弦的特征,又有固支的特征。
如图1所示,当k1、k3→+∞时,拉索两端弹性嵌固,此时边界条件可认为是耦合了铰支边界条件和固支边界条件。对于极端情况:当拉索两端转动弹性约束(k2=k4=0)时,边界条件为铰支;而当拉索两端转动弹性约束(k2、k4→+∞)时,边界条件变为固支;因此,用弹性边界来描述铰支与固支的耦合是合适的,其频率方程如下:
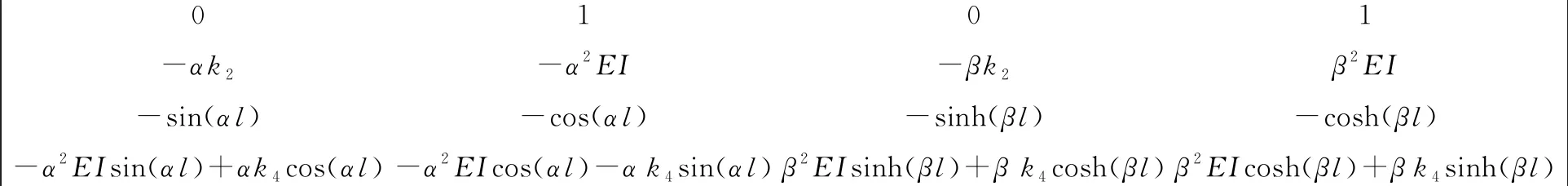
(5)
将式(5)写成多项式的形式为:
0
(6)
对于式(6),若k2=k4=0,则方程可简化成铰支边界条件下的索力计算公式;若k2、k4→+∞,则方程可简化为固支边界条件下的索力计算公式。这与理论模型边界条件的转化一致。因此,弹性边界同时包含了铰支与固支的情况,具有一定的普适性。
2 弹性边界的索力计算
弹性边界为铰支边界与固支边界的耦合,根据对称性,一般来说,式中支承刚度k2与k4相同,可将其统称为kr。因此,式(6)变为:
(7)
式(7)中包含了双曲函数因子cosh(βl)与sinh(βl),经计算发现,两双曲函数的值存在2个显著特征: ① cosh(βl)与sinh(βl)的值非常大,至少比αβ大10个数量级以上;②cosh(βl)与sinh(βl)的值极为相近,可认为两者相等。基于以上两点特征,将式(7)简化可得到:
(S2+2βS+2ζ2)tan(αl)-2αS-2γ2=0
(8)
(9)
与固支边界频率方程[2]成立的条件一样,式(8)也必须满足:
tan(αl)≥0
(10)
将式(8)代入式(9)可得:
(11)
将式(11)中α、β、ζ与S所包含的抗弯刚度设为EI0,并将其作为已知参数,将索力T作为变量,而等号左边的EI作为索力T的函数,频率ω取拉索基频,则式(11)变为:
(12)
定义一弹性支承刚度因子K:
K=lgkr
(13)
则
kr=10K
(14)
因此,本文通过式(12)及逆过程求解索力T。
3 索力计算方法验证
设计拉索振动实验,其中,拉索长l=3.0 m,线密度m=0.238 6 kg /m,实际拉力TSJ=2 940 N。拉索振动波形及频谱如图2所示。前14阶频率值如表1所示。

图2 3.0 m拉索模型振动波形及频谱图
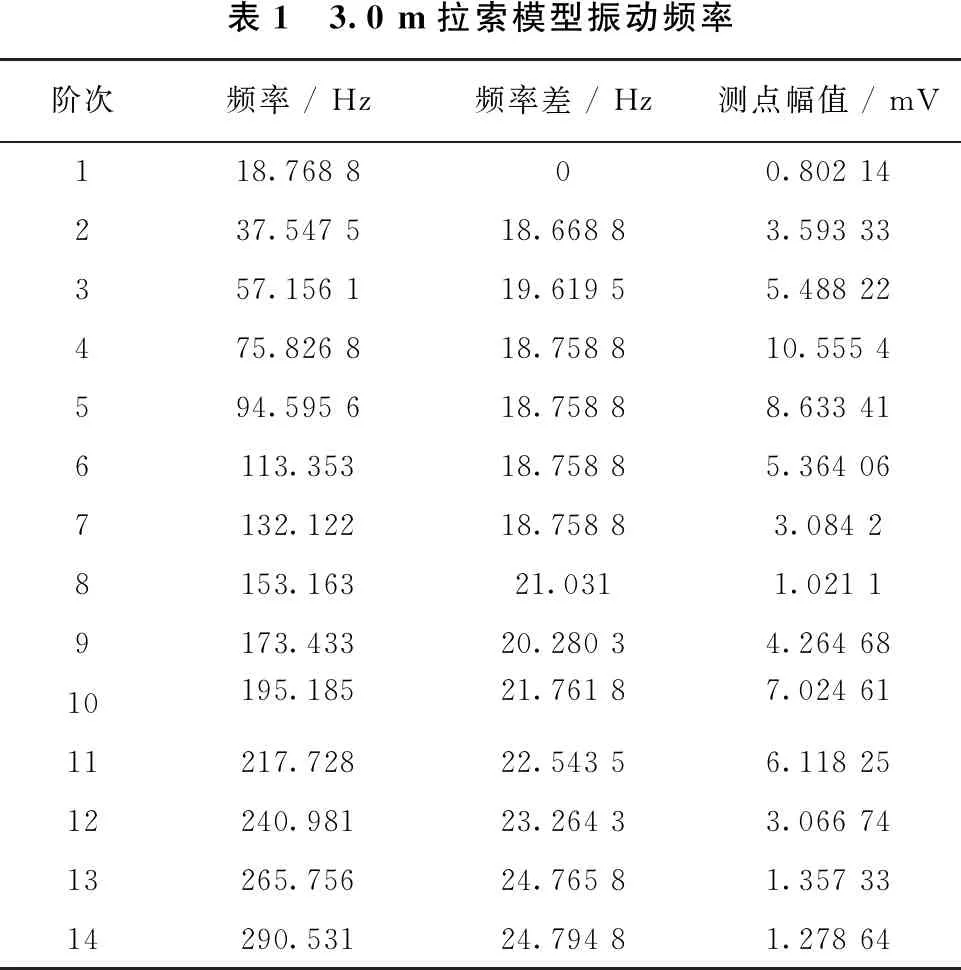
表1 3.0 m拉索模型振动频率阶次频率 / Hz频率差 / Hz测点幅值 / mV118.768 800.802 14237.547 518.668 83.593 33357.156 119.619 55.488 22475.826 818.758 810.555 4594.595 618.758 88.633 416113.35318.758 85.364 067132.12218.758 83.084 28153.16321.0311.021 19173.43320.280 34.264 6810195.18521.761 87.024 6111217.72822.543 56.118 2512240.98123.264 33.066 7413265.75624.765 81.357 3314290.53124.794 81.278 64
当EI0=2.42 N·m2时,可算得对应于不同支承刚度因子K的一组索力值,如表2所示,式(12)所描述的EI与T的关系曲线如图3所示。
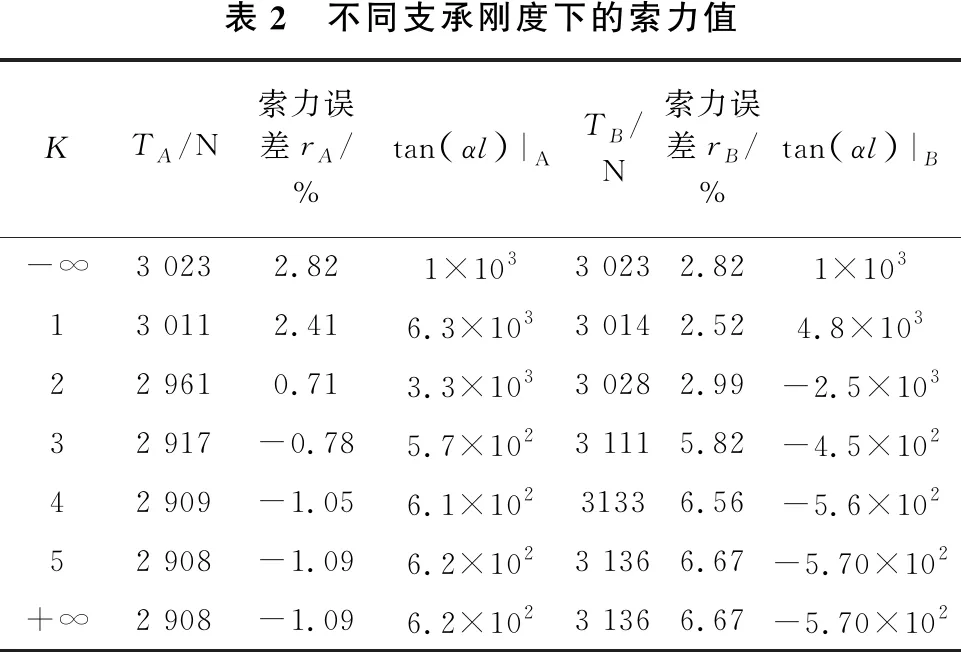
表2 不同支承刚度下的索力值KTA/N索力误差rA/%tan αl |ATB/N索力误差rB/%tan αl |B-∞3 0232.821×1033 0232.821×10313 0112.416.3×1033 0142.524.8×10322 9610.713.3×1033 0282.99-2.5×10332 917-0.785.7×1023 1115.82-4.5×10242 909-1.056.1×10231336.56-5.6×10252 908-1.096.2×1023 1366.67-5.70×102+∞2 908-1.096.2×1023 1366.67-5.70×102
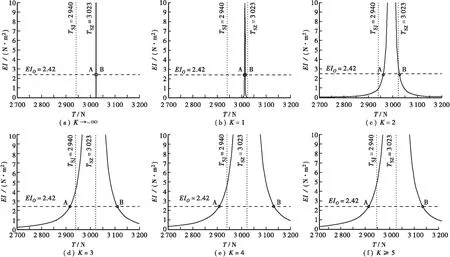
图3 弹性边界条件下的索力计算结果
当K→-∞即kr→0时,拉索变为铰支边界,直接使用铰支边界条件下的索力计算公式算得索力值TJZ=3 023 N,该计算结果符合表2结果。
由表2可知,索力计算值随支承刚度因子K增大而减小。但K超过5时,索力的计算值几乎不再变化。此时,该索力计算值与在固定边界条件下计算得到的索力值相等。由此可得,本文试验模型弹性支承因子K≥5时,可将其看作固支边界。当K非常小时,索力计算值TA、TB都能够满足式(10),但此时TA和TB几乎相等。所以,对于弹性边界条件下的索力计算,只需关注TA即可。
4 参数影响分析
对于弹性边界,索力与拉索抗弯刚度以及弹性支承刚度有关。因此,仍以上述拉索实验模型为例,设定区间K∈(0, 5],EI∈(0, 10],可绘出索力T与弹性支承刚度因子K、抗弯刚度EI的三维关系曲面,如图4所示。
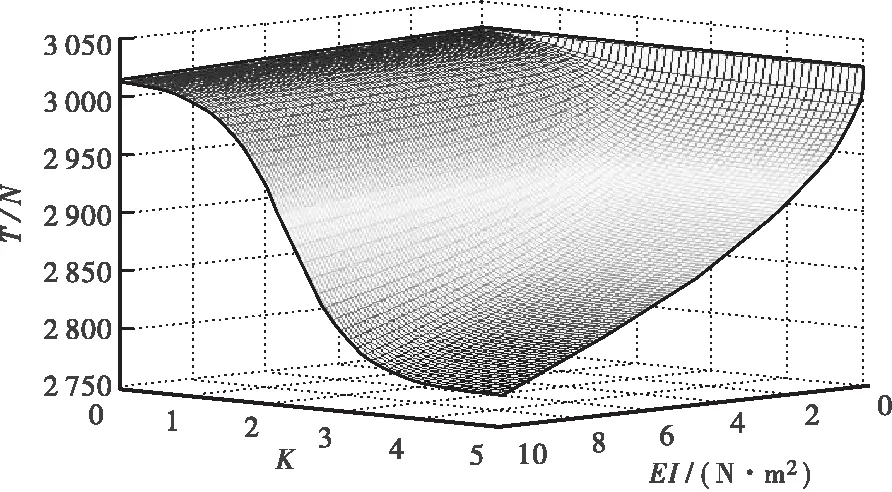
图4 T与K、EI的三维关系曲面
当K=0,1,2,3,4,5时,索力T与抗弯刚度EI的关系曲线如图5所示;当EI→0及EI=2,4,6,8,10时,索力T与弹性支承刚度因子K的关系曲线如图6所示。
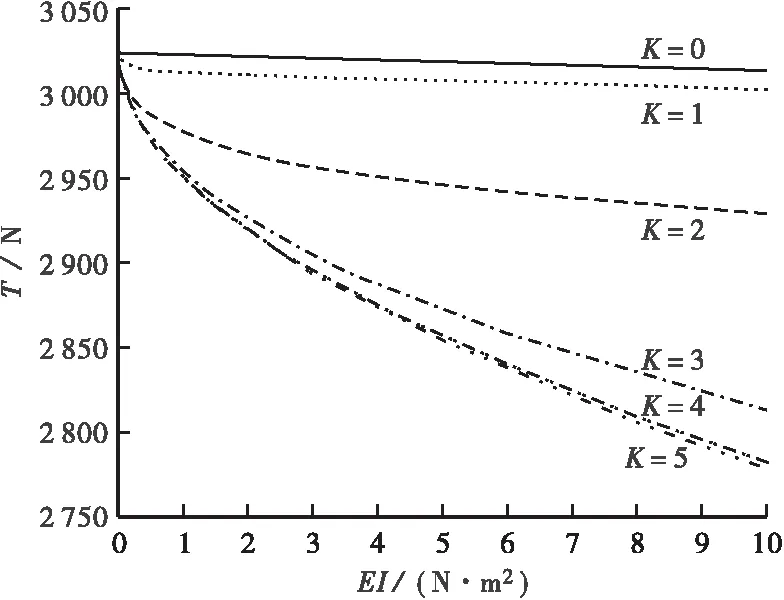
图5 T与EI的关系曲线
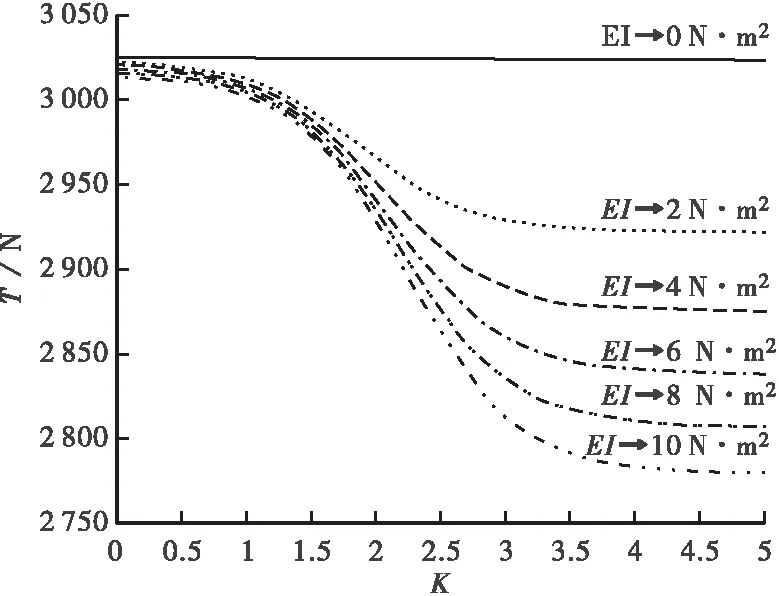
图6 T与K的关系曲线
根据图4~6可以得出结论:在确定的频率下,随着抗弯刚度EI增大,索力T减小;在确定的频率下,随着弹性支承因子K的增大,索力T同样减小;当K∈(1, 3.5)时,索力T变化较大,而K在该区间之外时,索力变化不大。弹性支承刚度因子K越大,索力T受抗弯刚度EI的影响越显著;抗弯刚度EI越大,索力T受弹性支承因子K的影响越显著。
5 结论
实际的索结构除考虑铰支及固支的情况,还需考虑弹性边界条件的情况。针对弹性边界条件下拉索索力计算问题,考虑弹性支承因子,给出了考虑弹性边界的索力求解方法。通过试验数据对计算方法进行验证,探讨了弹性支承刚度因子、抗弯刚度与索力T的关系。研究结果表明:
1) 本文所提出的索力求解方法具有较高精度,索力误差rA在3%以内。
2) 在确定频率下,随着抗弯刚度EI增大,索力T减小;在确定频率下,随着弹性支承因子K增大,索力T同样减小;
3) 当K∈(1, 3.5)时,索力T变化较大;当K在该区间之外时,索力变化不大。弹性支承刚度因子K越大,索力T受抗弯刚度EI的影响越显著;抗弯刚度EI越大,索力T受弹性支承因子K的影响越显著。
