压剪复合型弹性车轮轮轨接触关系研究

杨 阳，丁军君，李 芾，王孔明

(1. 中铁二院工程集团有限责任公司 科研院, 四川 成都 610031；2.西南交通大学 机械工程学院，四川 成都 610031)

轮轨接触关系是铁道车辆的独有特征，直接影响车辆的运行安全性，同样也是车辆、轨道系统中最基本、最复杂的问题[1-3]，对于轮轨接触关系学者主要关注的是轮轨接触几何关系及轮轨接触应力分布。

国内外学者对轮轨接触几何关系进行了大量的研究，早期的研究大多是将轮轨型面描述为直线或者几段圆弧，利用解析法获得轮轨几何约束关系。严隽耄[4]以三次样条函数为拟合曲线，采用最小距离搜索法研究任意轮廓形状的轮轨空间接触几何问题。王开文[5]等将车轮滚动圆上可能的接触点集合在一起形成一条空间迹线，代替轮轨接触几何关系中的实际踏面区域。Arnold[6]在轮轨接触计算的过程中引入接触点附近区域的变形，从而对实际的接触点进行修正和优化，使轮轨接触点的分布光滑连续。Sugiyama等[7]基于弹性接触理论，采用混合搜索算法研究轮轨接触点位置并应用于车辆系统动力学仿真。徐鹏等[8]利用对轮轨接触跳跃区域的二次扫描研究轮轨两点接触关系。对于轮轨接触应力分析最初主要是基于赫兹接触理论求得弹性解析解[9]，随着有限元分析技术的发展，学者开始采用有限元分析方法求解复杂工况下的轮轨接触应力问题。周素霞等[10]利用Ansys有限元分析软件建立轮轨三维弹塑性接触有限元模型，对其曲线通过性能及轮轨接触应力进行计算分析。

在前期的轮轨接触关系分析中，都是以传统刚性轮对为研究对象，即轮对中左右车轮和车轴是一个整体。但对于弹性车轮，由于轮毂和轮芯之间有橡胶元件且在运用过程中会发生变形，因此左右车轮和车轴不再是一个整体，相比刚性车轮，其轮轨接触关系更为复杂。本文以压剪复合型弹性车轮为例，研究弹性车轮的轮轨接触关系特点及影响因素，并与刚性车轮进行比较。

1 弹性车轮轮轨接触应力

1.1 弹性车轮基本结构

为了减振和降噪，压剪复合型弹性车轮的轮毂和轮芯之间设置橡胶元件，其结构见图1。弹性车轮的轮芯和轮毂是两个独立的部件，由橡胶元件提供连接刚度，同时左右车轮的轮芯均与车轴过盈配合，因此左右车轮的轮毂均相对于车轴或轮芯有6个自由度，即相对于x、y、z方向的平移自由度和旋转自由度。轮毂相对于轮芯在x、y、z方向的横移量分别为lx、ly、lz，在x、y、z方向的偏转角度分别为βx、βy、βz。对于刚性车轮，横移量和偏转角度均为0。

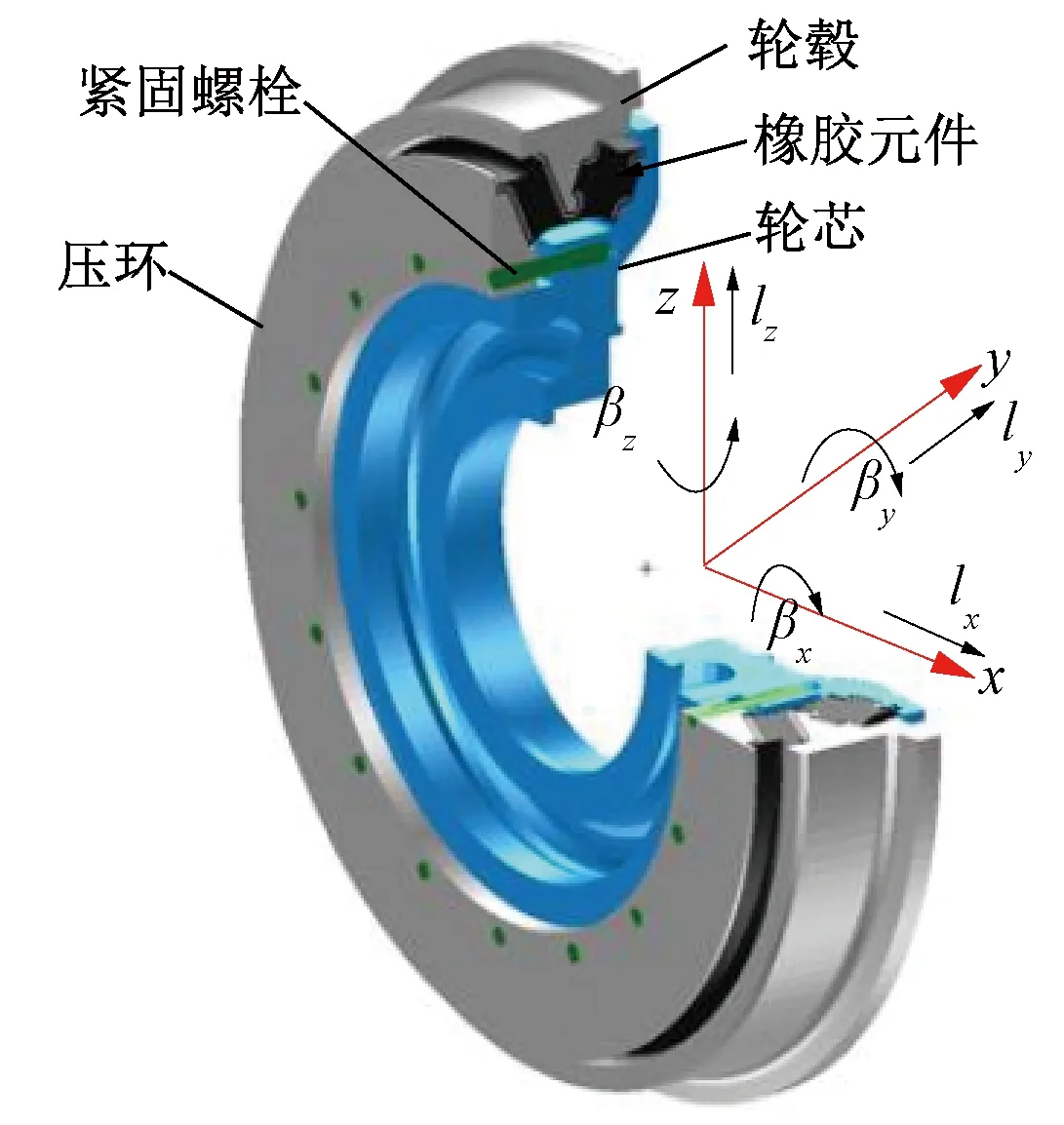
图1 压剪复合型弹性车轮结构示意图

1.2 轮轨接触应力计算模型

在轮轨接触斑内部应力较大，材料可能发生塑性变形，因此在进行分析计算时采用能够模拟材料塑性变形的双线性随动强化弹塑性模型[11]，屈服条件为Mises屈服准则。橡胶元件采用Mooney-Rivlin本构模型进行模拟。

基于Abaqus有限元分析软件建立弹性车轮有限元模型，见图2。

图2 弹性车轮有限元模型

国内某低地板有轨电车踏面及59R2槽型轨的轮轨接触应力分析模型见图3，为提高计算效率同时又不损失计算精度，轮轨接触区域及其附近的网格划分细密，其他区域的网格划分较为稀疏。

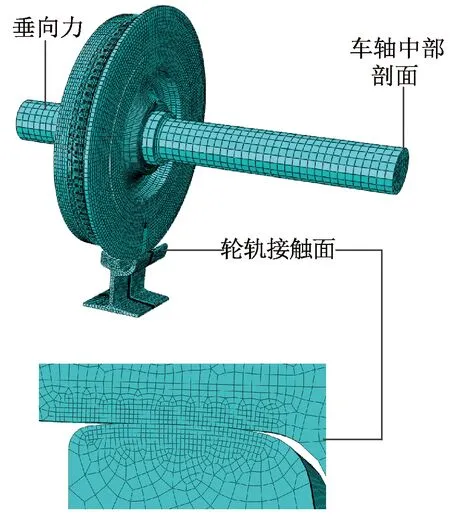
图3 弹性车轮轮轨接触模型

1.3 计算结果

车轮轮轨接触关系计算结果见表1，结果显示弹性车轮较刚性车轮轮轨接触斑面积增加16.87%。由于轮轨接触斑面积增加，弹性车轮较刚性车轮最大接触压力降低31.66 MPa，轮轨最大Mises等效应力降低19.91 MPa，即分别降低了3.54%和4.5%。这主要是由于弹性车轮轮芯和轮毂之前安装了橡胶元件，当在外力作用下弹性车轮轮毂相对于轮芯发生偏转，且弹性车轮踏面及轨面均为不规则形状，造成接触点变成两个，接触面积增加，见图4(a)，同时也造成了两个应力集中区域。刚性车轮无法发生倾斜，仅有一个应力集中区域见，图4(b)。

表1 轮轨接触仿真计算结果

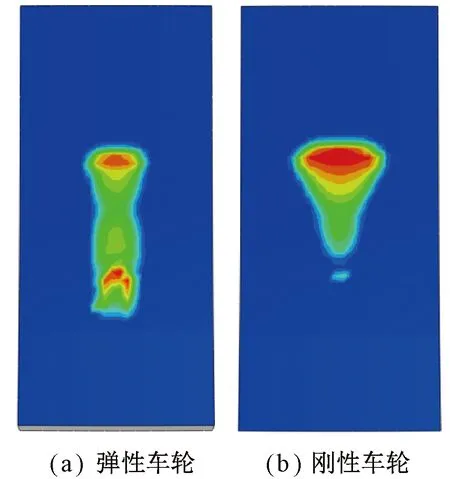
图4 最大接触压力分布

轮轨最大Mises等效应力分布见图5，刚性车轮等效应力较弹性车轮高应力区域分布更深，这主要是由于刚性车轮轮轨最大Mises等效应力较弹性车轮高造成的。

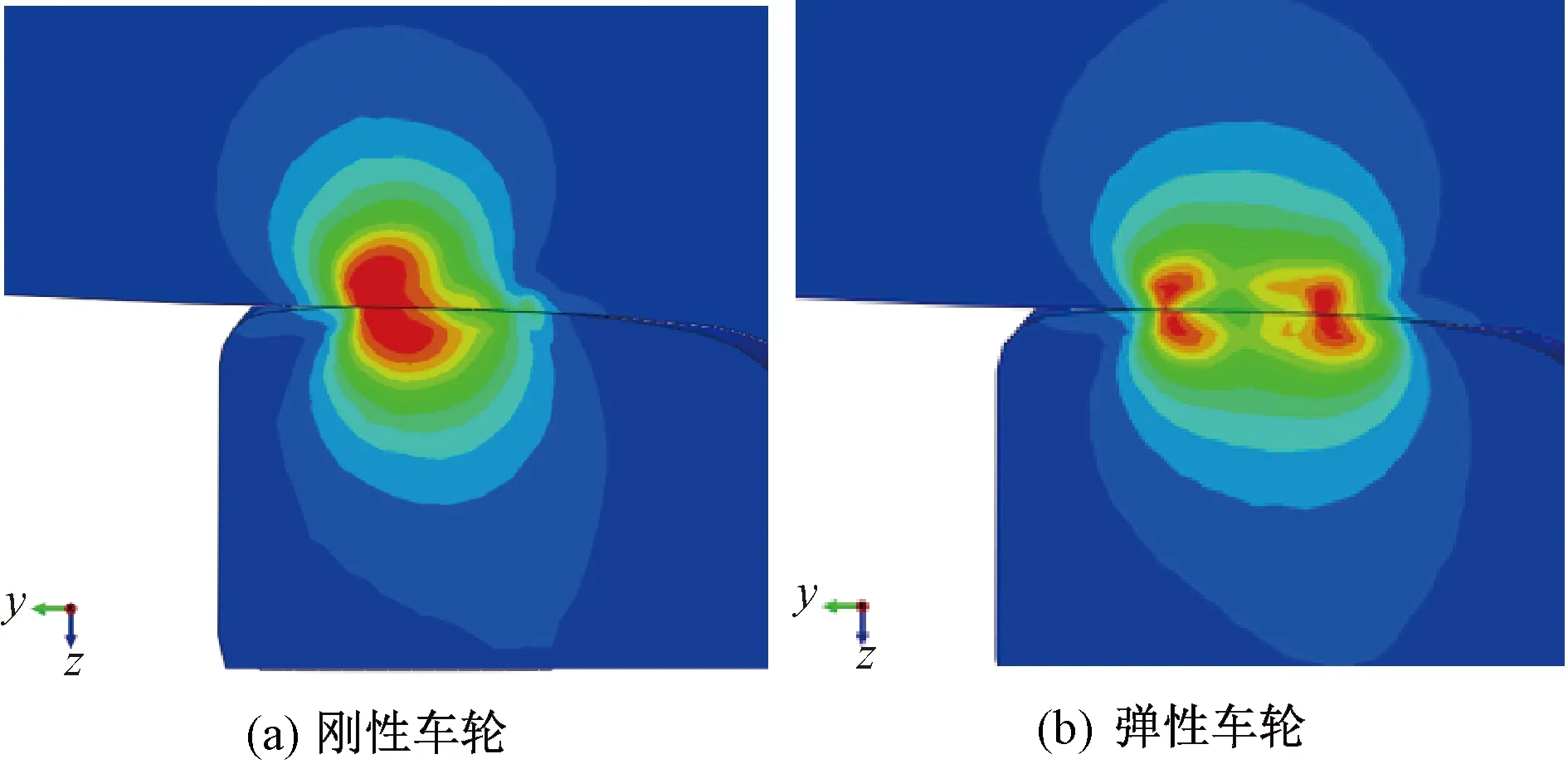
图5 Mises等效应力分布图

2 弹性车轮轮轨接触几何关系

2.1 轮轨接触几何关系的评估方法

轮轨接触几何关系主要包括单一轮轨接触点位置和大量接触点位置的累积分布，而在实际工程运用中，大量轮轨接触点位置累积分布的研究更有实际意义。因此，为了比较弹性车轮和刚性车轮对应的累积轮轨接触点位置分布特征，本文采用Pearson线性相关系数的方法进行评估。

Pearson相关系数被广泛用于度量两个变量m和n之间线性相关性的强弱[14-15]，其定义为

(1)

式中：γ为相关系数；E为变量的期望；μm和μn分别为变量m和n的均值；σm和σn分别为变量m和n的标准差。

通常|γ|≤1，且|γ|越接近1，表示两接触点分布曲线的相似性越高。当0<|γ|<0.3时成为微弱相关，0.3<|γ|<0.5时为低度相关，0.5<|γ|<0.8时为显著相关，0.8<|γ|≤1时为高度相关。

2.2 弹性车轮动力学模型

对于刚性车轮，影响车轮型面坐标的主要因素是轮对横移和侧滚等参数，而对于弹性车轮，除了轮对横移和侧滚外，还受轮芯和轮毂之间相对位移和偏转角度的影响。为获得车轮的运动数据，基于Simpack多体动力学软件建立弹性车轮的车辆动力学模型，见图6。其中弹性车轮的轮对动力学模型包括一根车轴、两个轮芯、两个轮毂和两个轴箱，见图7。轮芯相对于轮毂具有图1所示的6个方向自由度，轮芯和轮毂相互独立，通过力元体现橡胶元件的刚度特性。每个轮毂与车轴之间均有一个绕y方向旋转的自由度，并设置对应的扭转刚度，用于模拟左右轮毂相对于车轴有不同的扭转角度。为便于对比弹性车轮和刚性车轮的轮轨接触位置，可在图6中动力学模型的基础上，将弹性车轮更换为刚性车轮。

图6 车辆动力学模型

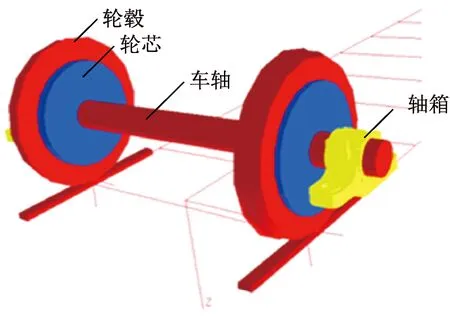
图7 弹性车轮动力学模型

根据弹性车轮的结构特点，橡胶元件在x方向和z方向的水平刚度相同，统称为径向刚度，y方向的水平刚度称为轴向刚度[16]。绕x方向和z方向的旋转刚度相同，统称为偏转刚度，绕y方向的旋转刚度称为扭转刚度。弹性车轮的各向等效刚度通过弹性车轮相关试验测量获得，具体见表2。

2.3 轮轨接触几何关系计算结果

2.3.1 直线上的轮轨接触关系对比

对采用弹性车轮和刚性车轮的车辆动力学模型在直线工况下进行仿真，运行速度为80 km/h，轨道激励为美国五级谱。以前转向架导向轮对为例，弹性车轮的轮对中心横向偏移量和轮轨横向力的均方根值(RMS值)分别为3.028 mm和2.21 kN，刚性车轮的分别为3.076 mm和2.74 kN，弹性车轮的轮轴横向力略小于刚性车轮，而轮对中心横向偏移量相差不大。

由于轮轨接触点位置随着轮对的运动随时发生变化，因此根据动力学计算结果，对所有的轮轨接触位置进行统计并映射到车轮和钢轨对应位置，分别见图8和图9。在直线工况下，橡胶元件变形对车轮和钢轨上接触位置分布的影响很小，车轮上接触位置分布在-7.5～28.5 mm之间，钢轨上接触点位置分布在6.5～26.5 mm之间，相关系数分别为0.983 2和0.989 7，均属于高度相关，因此，在直线上弹性车轮的轮轨接触关系无需考虑橡胶元件弹性变形的影响；刚性车轮对应的轮轨接触分布与弹性车轮十分接近，相关系数分别为0.995 4和0.999 1，均属于高度相关。

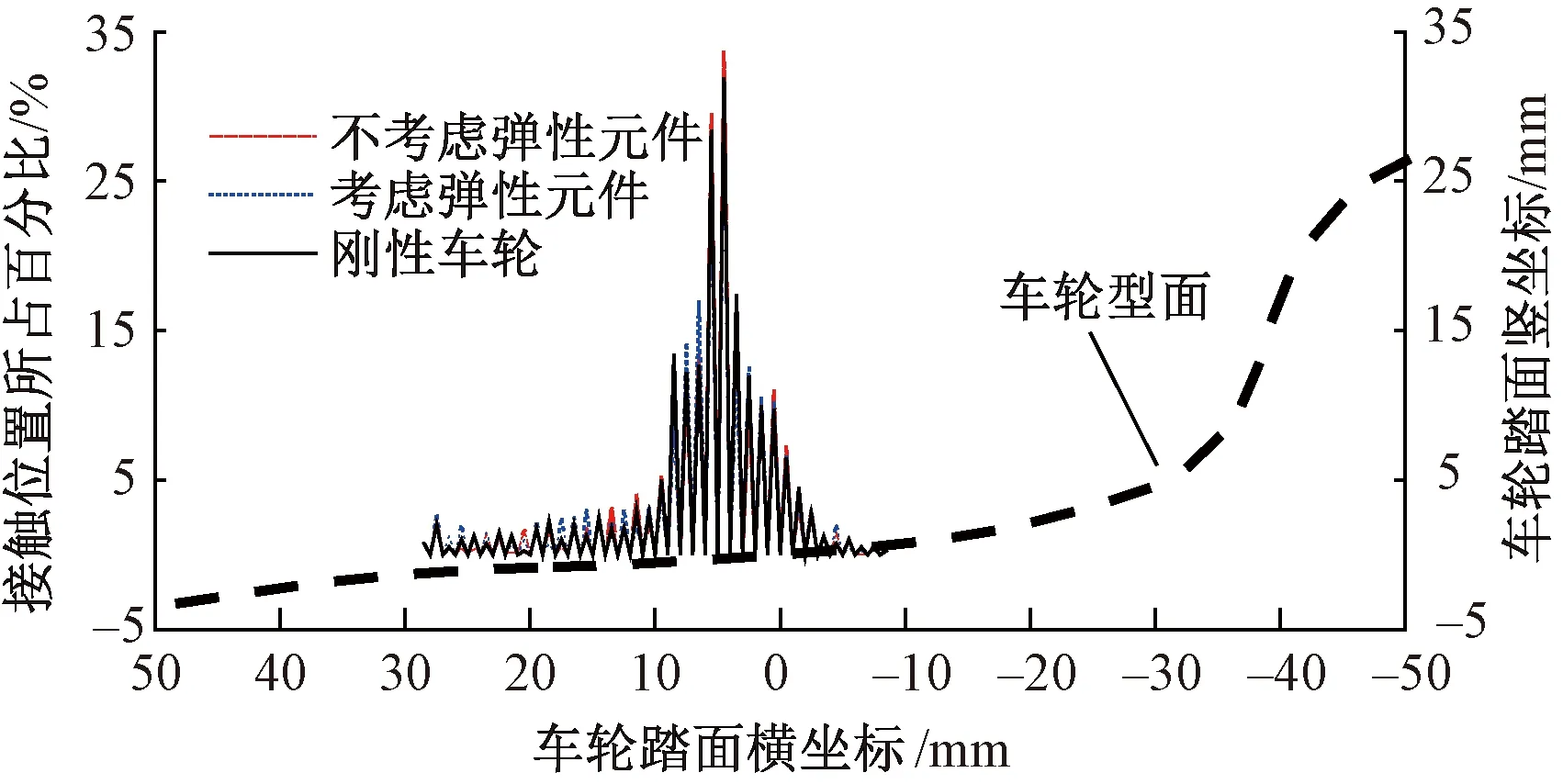
图8 直线上车轮接触位置对比

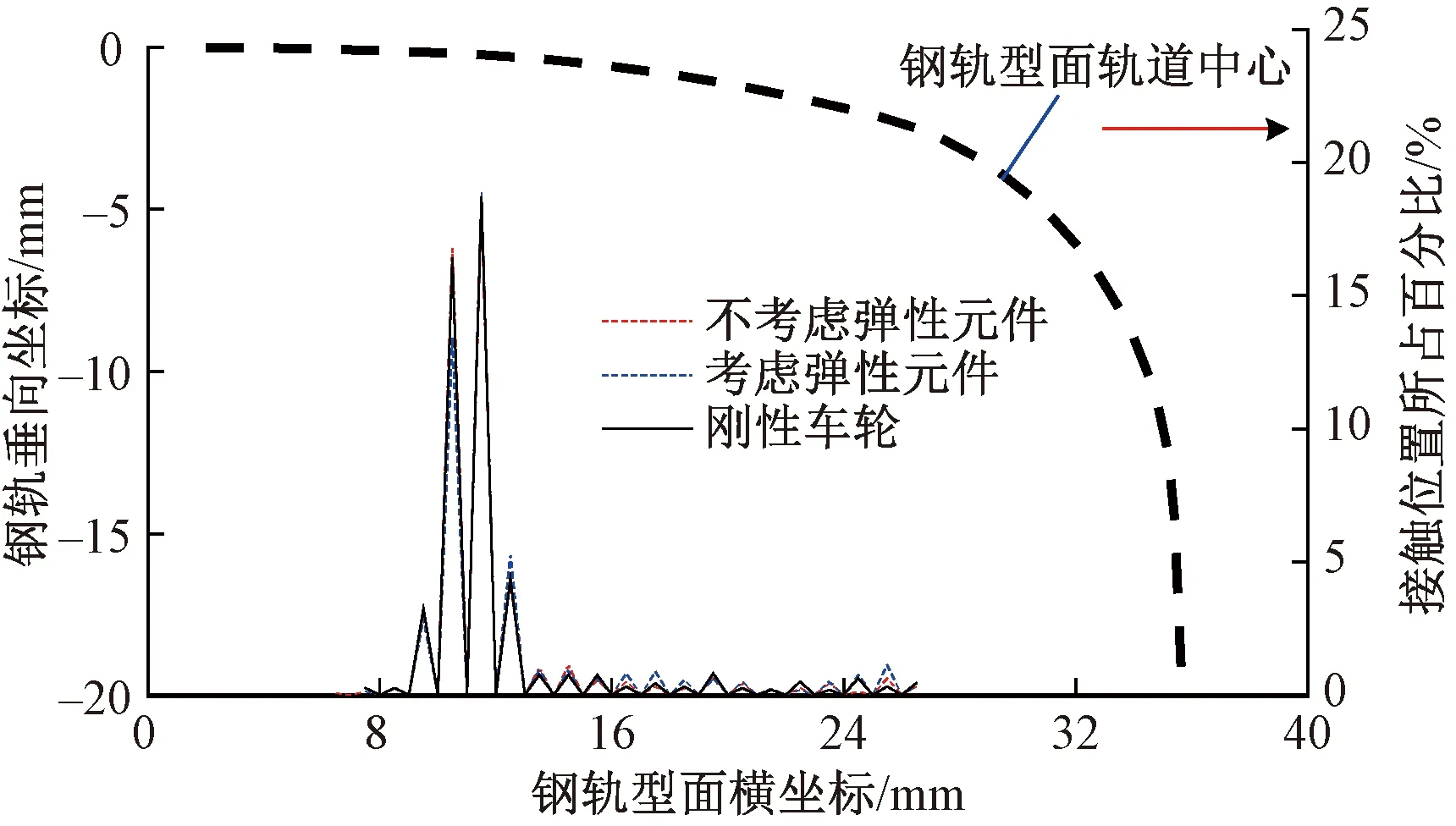
图9 直线上钢轨接触位置对比

2.3.2 曲线上的轮轨接触关系对比

当车辆以65 km/h在半径为300 m的曲线上运行时，其中轨道激励为美国五级谱，前转向架导向轮对的横移量和轮轴横向力，分别见图10和图11。与刚性车轮相比，弹性车轮的轮轴横向力有一定程度的下降，但轮对中心横向偏移量明显增大。在曲线中部，弹性车轮的轮对中心横向偏移量比刚性车轮大4 mm左右。车辆在通过曲线时受到较大的轮轨横向力，弹性车轮轮芯相对于轮毂之间发生较大的横向变形，造成了弹性车轮的轮对中心横向偏移量大于刚性车轮。同时轮对中心横向偏移量变大，导致轮轨接触关系发生较大变化。

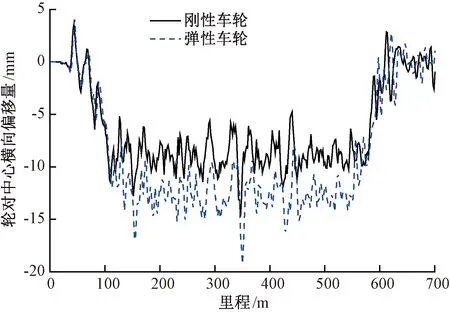
图10 曲线上的轮对中心横向偏移量对比

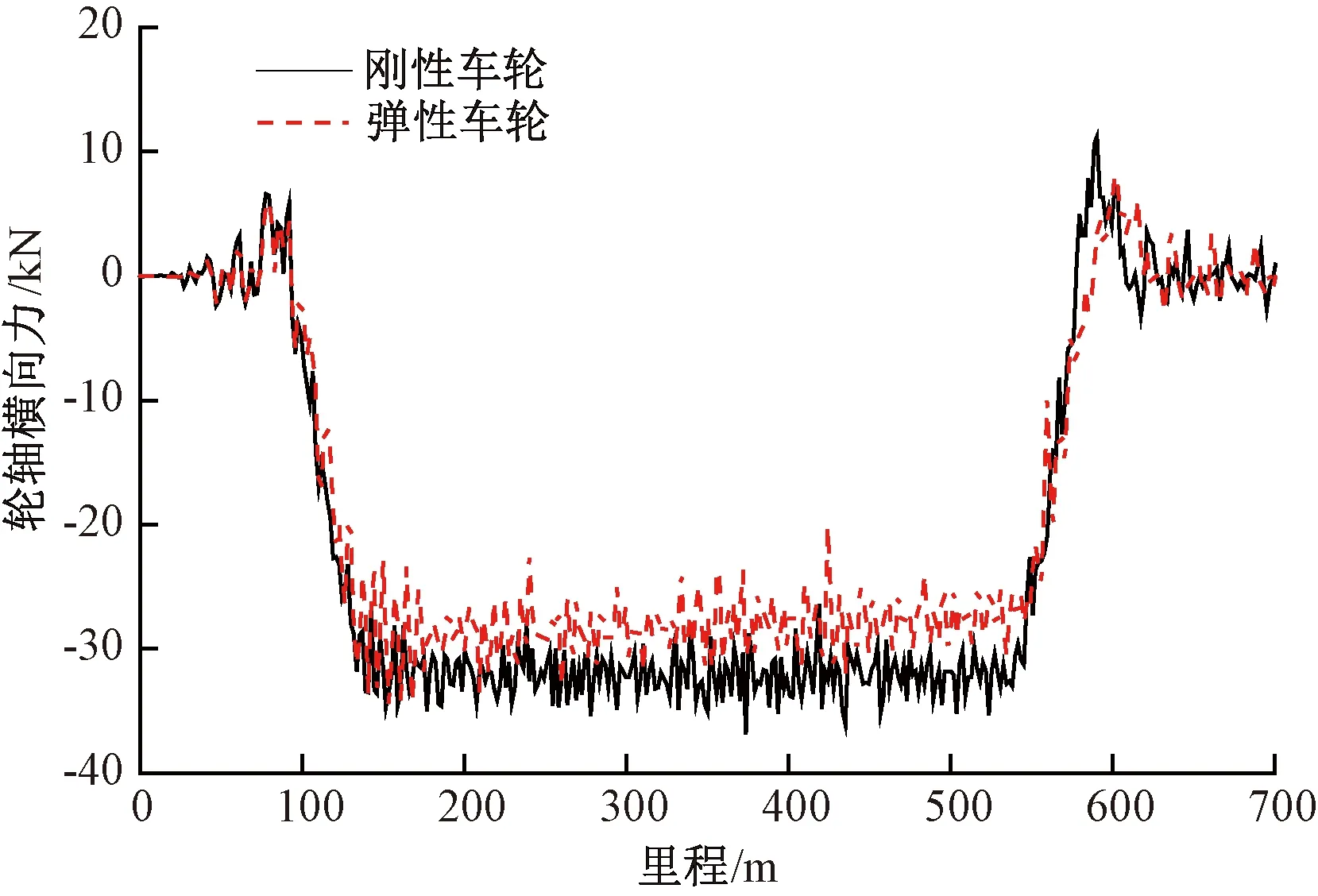
图11 曲线上的轮轴横向力对比

曲线上车轮和钢轨上的接触点分布范围分别见图12和图13。与直线工况相比，橡胶元件变形对轮轨接触关系已有一定的影响；在曲线外侧，车轮和钢轨上的轮轨接触分布相关系数分别为0.971 0和0.910 6；在曲线内侧，相关系数分别为0.964 1和0.843 8，同时不考虑弹性变形时的车轮接触点更加集中于踏面外侧(远离轮缘)。虽然曲线外侧和内侧的相关系数都大于0.8，属于高度相关，但是可以看到轮轨接触位置等已发生了变化，因此在轮轨接触关系分析中应考虑橡胶元件弹性变形的影响。

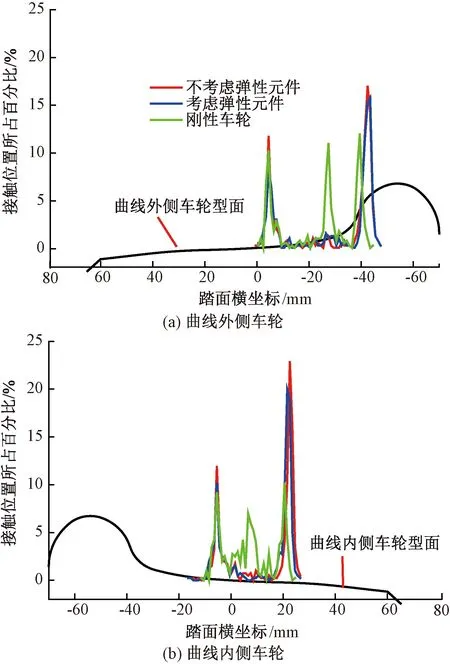
图12 曲线上车轮的接触点位置分布

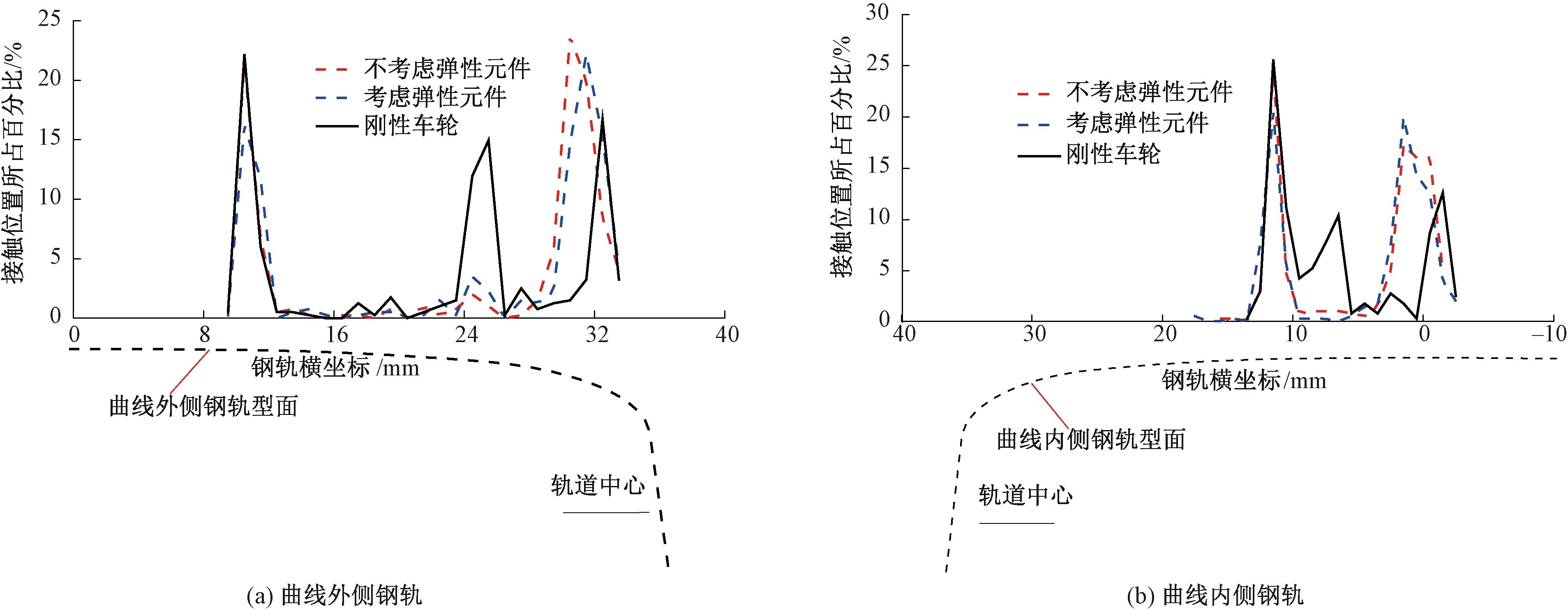
图13 曲线上钢轨的接触点位置分布

刚性车轮在曲线上的轮轨接触位置与弹性车轮有明显的区别，以曲线外侧的车轮为例，弹性车轮的接触点主要集中在-4.7、-42.7 mm，而刚性车轮的接触点主要集中在3个位置点：-4.7、-27.4、-39.5 mm；刚性车轮的接触点分布范围较弹性车轮明显收窄，值得注意的是，曲线外侧弹性车轮上的接触点更加靠近车轮轮缘，意味着更易发生轮缘磨耗和钢轨侧磨；刚性车轮与弹性车轮的对应的车轮上接触位置分布相关系数分别为0.192 7和0.248 6，属于微弱相关，对应的钢轨接触位置分布相关系数分别为0.343 4和0.415 8，均属于低度相关。

3 弹性车轮刚度对接触几何影响

根据弹性车轮的结构特点，对轮轨接触及磨耗产生影响的主要因素是橡胶元件轴向刚度和偏转刚度[17-18]。以车辆在曲线上运行为例，分析橡胶元件轴向刚度和偏转刚度对轮轨接触几何关系的影响。

3.1 轴向刚度的影响

弹性车轮轮对中心横向偏移量和摇头角随橡胶元件轴向刚度的变化，分别见图14和图15。轮对中心横向偏移量和摇头角的最大值和RMS值均随着橡胶元件轴向刚度的增大而减小，当刚度达到20 MN/m时，横移量和摇头角逐渐趋于稳定。

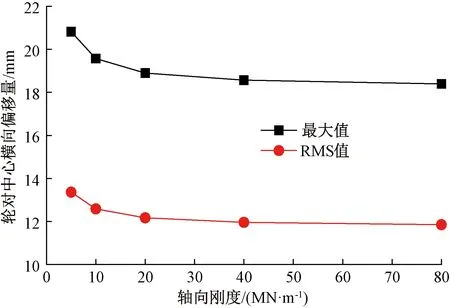
图14 轴向刚度对轮对中心横向偏移量的影响

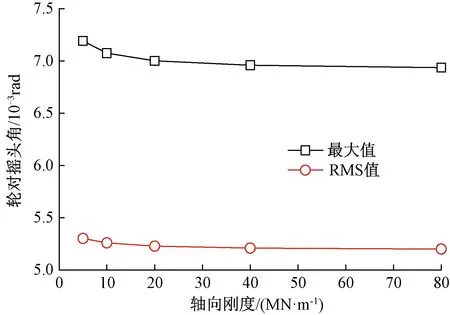
图15 轴向刚度对轮对摇头角的影响

在不同的轴向刚度条件下，橡胶元件变形因素对轮轨接触位置分布相关系数的影响见表3。随着轴向刚度的增加，曲线外侧车轮和钢轨上的轮轨接触分布相关系数均有明显的增加，而曲线内侧的相关系数增幅不大；当轴向刚度为5、10 MN/m时，曲线外侧车轮上的轮轨接触分布相关系数小于0.8，仅为显著相关；当轴向刚度在20 MN/m以上时，达到高度相关。

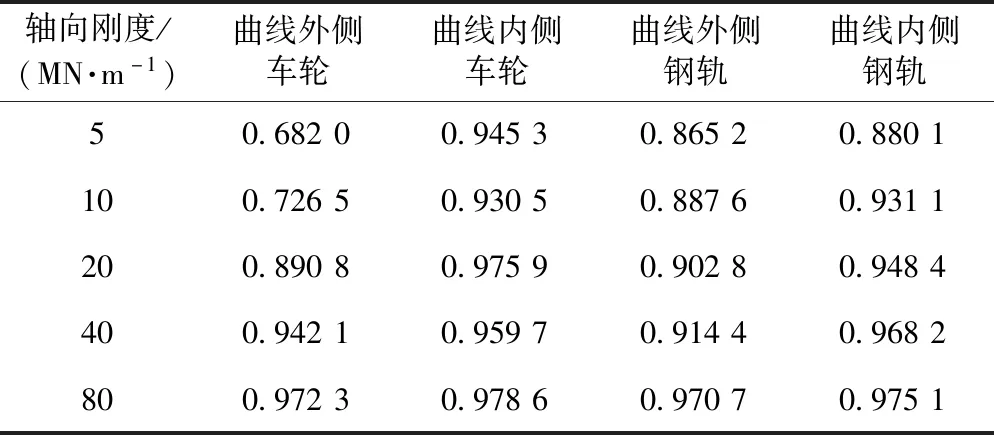
表3 轴向刚度对轮轨接触相关系数影响

不同轴向刚度下曲线外侧车轮的轮轨接触分布见图16。当轴向刚度较小时，橡胶元件变形对轮轨接触关系有较明显的影响，不考虑橡胶元件变形时的接触点位置更加靠近车轮轮缘，而当轴向刚度较大时，橡胶元件变形对轮轨接触关系影响较小。轴向刚度越小，车轮上的接触位置越靠近轮缘。

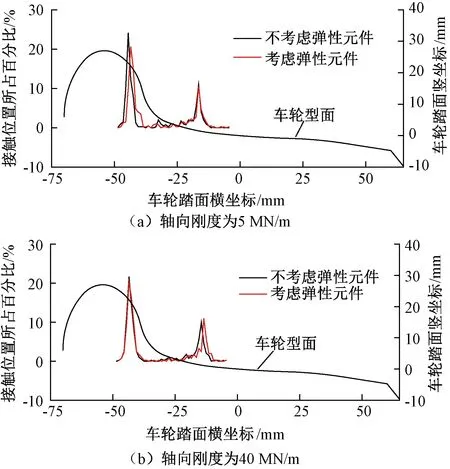
图16 不同轴向刚度下的轮轨接触位置分布

不同轴向刚度下曲线外侧车轮的磨耗功及脱轨系数见图17。随着轴向刚度的增加弹性车轮的磨耗功降低，脱轨系数增加。当弹性车轮轴向刚度从5 MN/m增加到80 MN/m时，脱轨系数仅增加了0.04，增加量较小，且脱轨系数最大值为0.48，即使弹性车轮刚度增加但是车辆的安全性仍然满足要求。综合考虑弹性车轮磨耗功、脱轨系数及轮缘贴靠问题，建议弹性车轮橡胶元件的轴向刚度取值为20～40 MN/m。

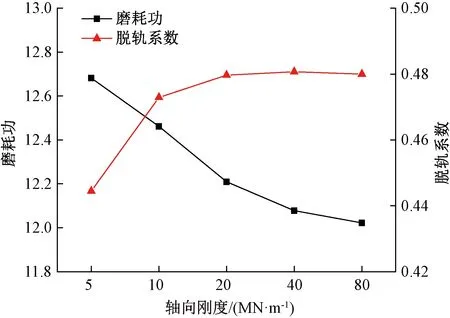
图17 不同轴向刚度下的磨耗功和脱轨系数

3.2 偏转刚度的影响

弹性车轮轮对中心横向偏移量和摇头角随轴向刚度的变化分别见图18和图19。轮对中心横向偏移量和摇头角的最大值和RMS值均随着橡胶元件偏转刚度的增大而减小，其减小的幅值随着偏转刚度的增加而逐渐减小。

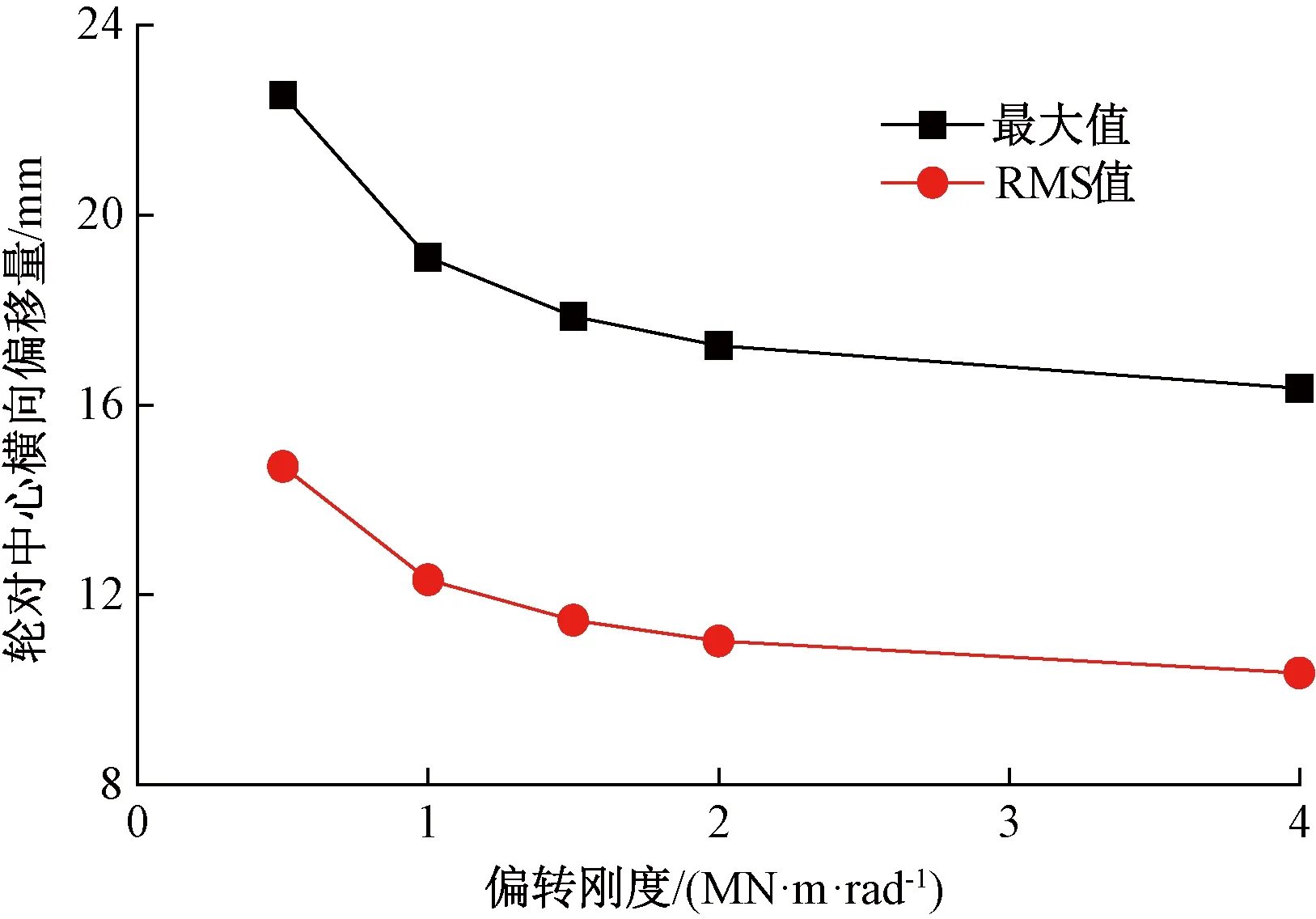
图18 偏转刚度对轮对中心横向偏移量的影响

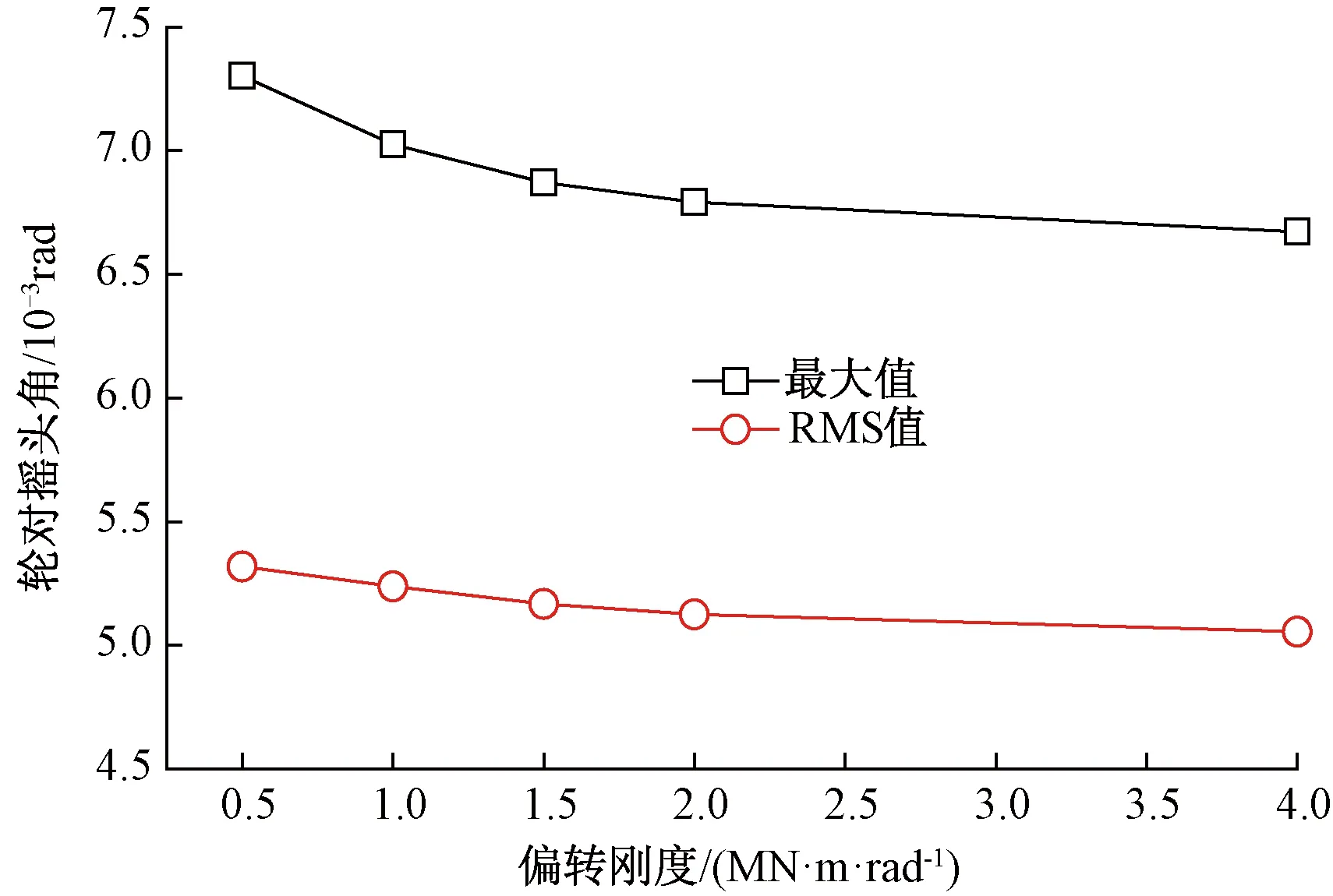
图19 偏转刚度对轮对摇头角的影响

在不同的偏转刚度条件下，橡胶元件变形因素对轮轨接触位置分布相关系数见表4。曲线外侧车轮和钢轨上的轮轨接触分布相关系数随着偏转刚度的增大均有明显的提高，而曲线内侧的相关系数增幅不大；当偏转刚度为0.5 MN·m/rad时，曲线外侧车轮上的轮轨接触分布相关系数小于0.5，仅为低度相关；当轴向刚度在1.5 MN·m/rad以上时，达到高度相关。

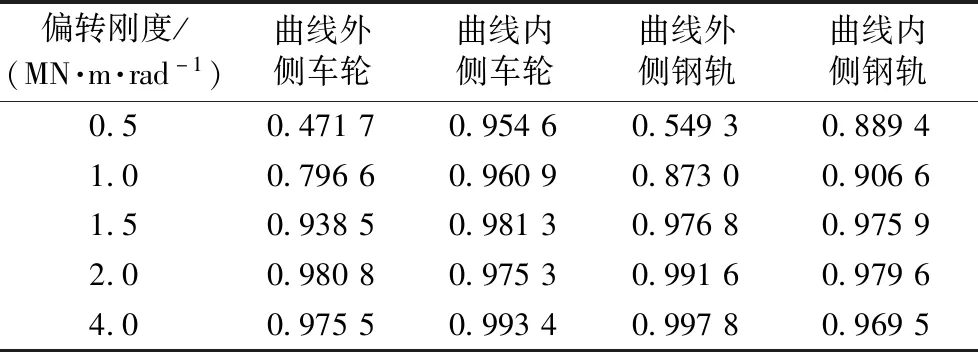
表4 偏转刚度对轮轨接触相关系数影响

不同偏转刚度下曲线外侧车轮的轮轨接触分布见图20。当偏转刚度较大时，弹性元件变形对轮轨接触关系影响较小，而当偏转刚度较小时，弹性元件变形对轮轨接触关系有较明显的影响，不考虑弹性元件变形时的接触点位置更加靠近车轮轮缘。偏转刚度越小，轮轨接触位置越靠近轮缘。

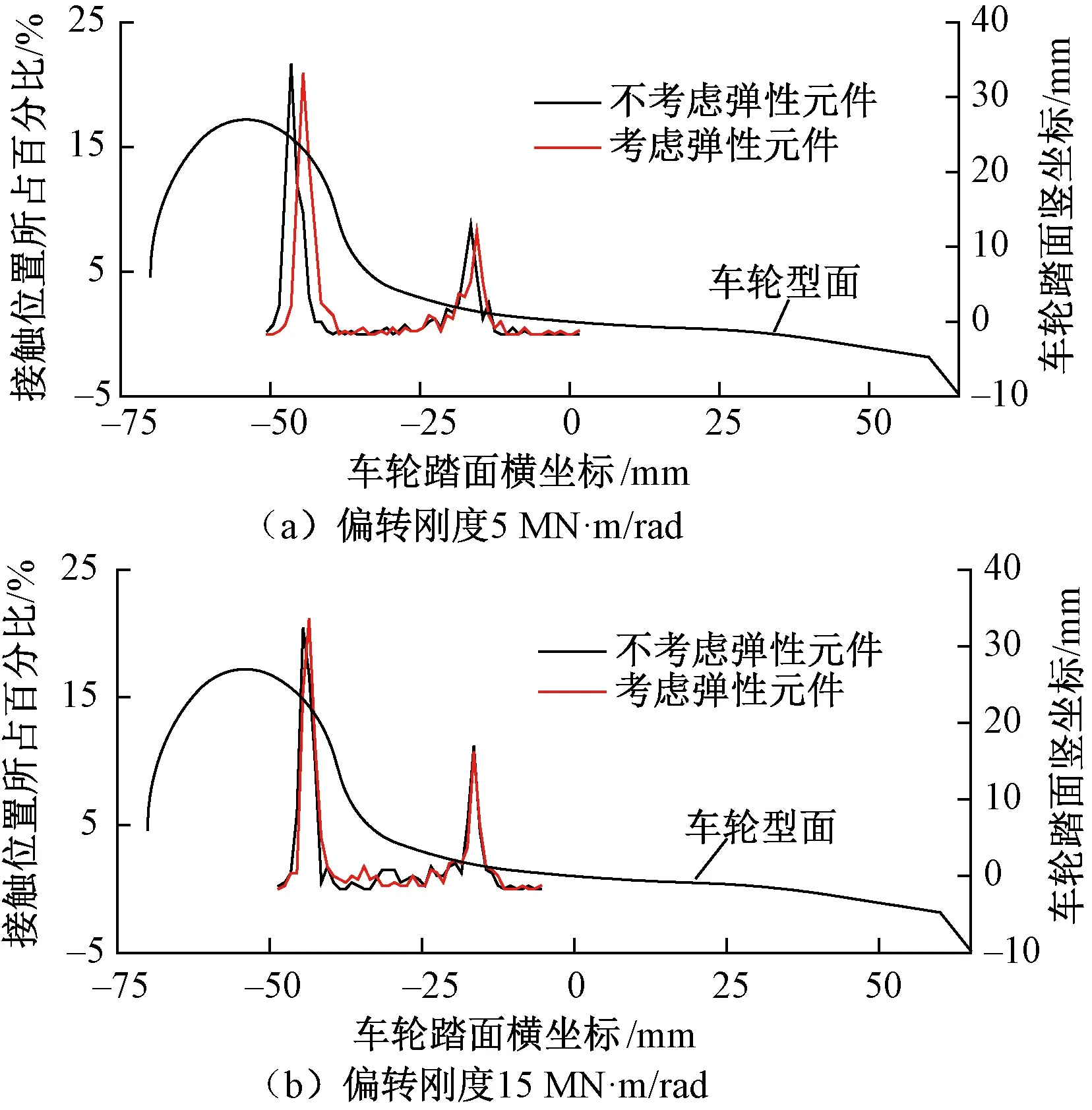
图20 不同偏转刚度下的轮轨接触位置分布

不同偏转刚度下曲线外侧车轮的磨耗功及脱轨系数见图21。随着偏转刚度的增加弹性车轮的磨耗功和脱轨系数均增加。当弹性车轮偏转刚度从0.5 MN·m/rad增加到4 MN·m/rad时，脱轨系数仅增加了0.07，增加量较小，且脱轨系数最大值为0.48，即使弹性车轮刚度增加但是车辆的安全性仍然满足要求。由于磨耗功评价的是整个踏面的磨耗情况，所以磨耗功无法单独体现当偏转刚度较小时轮缘贴靠造成的磨耗问题。综合考虑弹性车轮磨耗功、脱轨系数及轮缘贴靠问题，建议弹性车轮橡胶车轮的偏转刚度取值1.5 MN·m/rad以上。

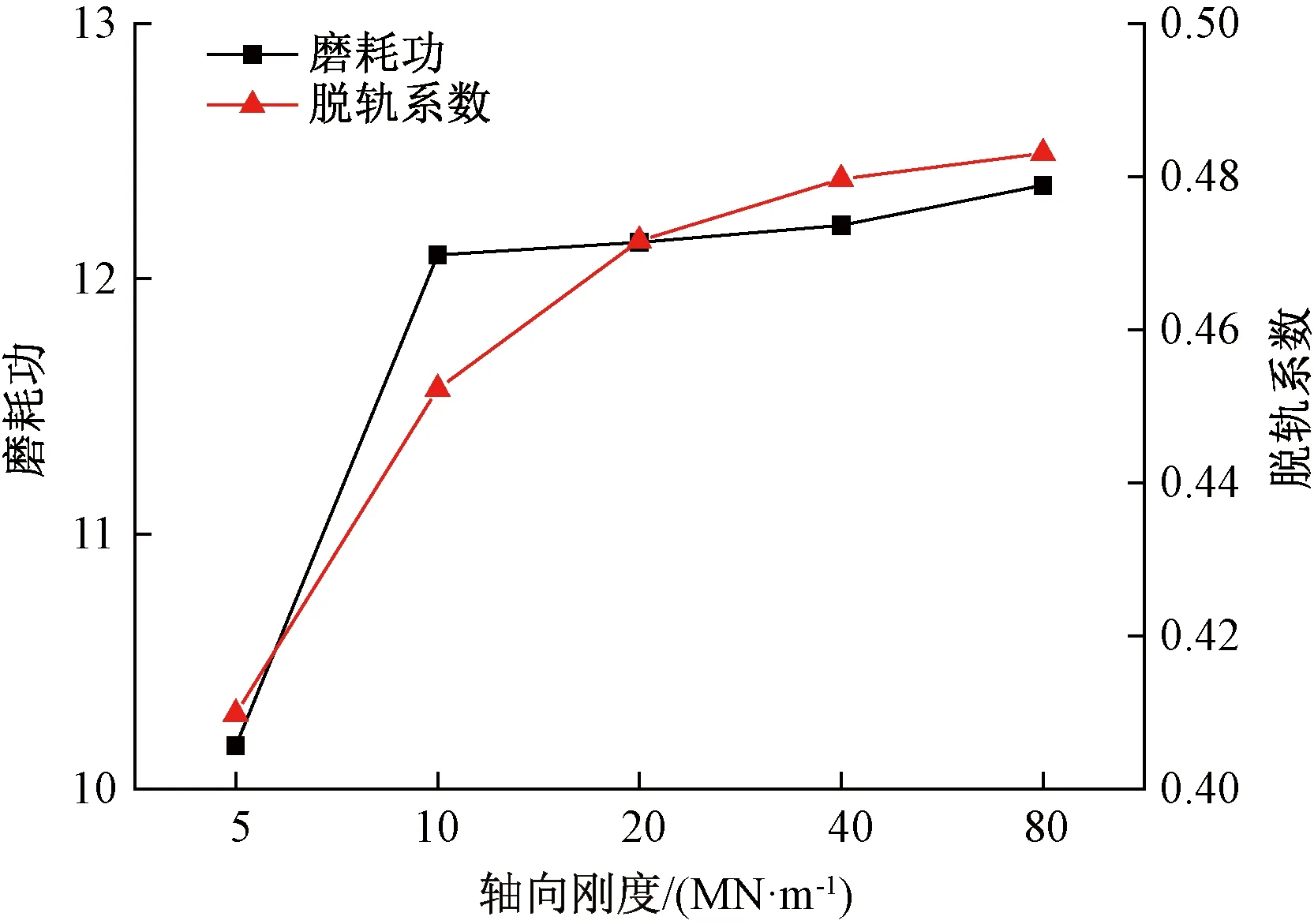
图21 不同偏转刚度下的磨耗功和脱轨系数

4 结论

(1)弹性车轮轮轨接触面积较刚性车轮接触面积增加16.87%，最大接触压力降低了3.54%，轮轨最大Mises等效应力降低4.50%。

(2)在直线工况下，弹性车轮与刚性车轮的轮轨接触分布高度相关，橡胶元件变形对弹性车轮轮轨接触位置的影响较小。

(3)在曲线工况下，橡胶元件变形对轮轨接触位置分布的影响取决于弹性车轮的轴向刚度和偏转刚度，当这两个刚度较小时，弹性元件变形对轮轨接触关系有较明显的影响，说明在进行车辆动力学计算时考虑橡胶元件的影响是十分必要的。同时弹性车轮与刚性车轮在曲线上的轮轨接触位置分布相关系数最低仅为0.192 7，属于微弱相关，而且弹性车轮在曲线外侧的接触点更加靠近车轮轮缘。

(4)曲线上弹性车轮虽然较刚性车轮能降低轮轴横向力，但较小的轴向刚度和偏转刚度会带来较大的轮对中心横向偏移量和摇头角，使轮轨接触位置更加靠近轮缘，为了避免异常轮轨磨耗，建议轴向刚度取值在20～40 MN/m之间，偏转刚度取值在1.5 MN·m/rad以上。若轴向刚度及偏转刚度取值不当将会造成掉轨、轮轨异常磨耗等问题，对车辆运行安全性、经济性造成一定的影响。