《GRADE在网状Meta分析不精确性的处理》文献解读
2021-03-12杨智荣王巍巍刘凤琪
李 戈 杨智荣 王巍巍 刘凤琪 李 沛 孙 凤
1 主要内容介绍
本指南项目组隶属于GRADE工作组,认为从不精确性角度对网状Meta分析(NMA)证据体的确定性进行评估与传统Meta分析证据分级遵循相同的基本逻辑,但是NMAs估计值的有效样本量估算方法不同,且可根据效应量大小决定是否有必要计算最佳信息样本量(OIS),并首次提供了NMAs的OIS实用算法,系统评价制作者应根据本指南评估网状Meta分析证据体的不精确性。
系统评价制作者在评估NMAs估计量的不精确性时需要兼顾具体场景、可信度评级的目标、预设阈值、95% CI与阈值的关系、效应量大小以及OIS。当95%CI包含预设阈值,可考虑降级;当95%CI不包含阈值且效应量大小适中时,无需考察OIS,不因不精确性而降级;当95%CI不包含阈值且效应量大时,需考察OIS,如满足OIS, 则不因不精确性而降级,反之因不精确性降级。
若不精确性是由另一个降级因素导致,应避免重复降级。
项目组提供了一份excel文档,系统评价制作者可采用其中的工作表计算NMA估计值的OIS和有效样本量。
2 重要观点及解读
系统评价制作者和指南制定者处理不精确性的通用步骤:
(1)明确关键信息,即根据系统评价目的及决策情境进行效应量阈值判断:零效应量(0)、小效应量(a)、中等效应量(b)及大效应量(c)。
(2)考虑效应量CI界值与情境阈值关系:当CI完全位于某个阈值的一侧或两个阈值之间,则更有信心确定疗效价值[1];而当CI包含特定阈值时,证据可信度降低。图1所示,根据最低情境法,即存在任何效应(CI未包括0阈值)进行评估:CI1-3均不因不精确性而降级;根据存在至少小效应量评估:则CI1降级,而CI2-3不降级;根据分步情境法,如果评级目标是小效应,则CI1或CI3因不精确性降级,而CI2不降级。但是,当CI包含阈值时是否对不精确性进行降级,取决于研究场景、可信度评估目标和所选阈值[1],如在等效试验中当评估目的为是否存在双侧轻微效应,抑或无差异,那么当CI4完全处于微小获益和微小伤害阈值之内时,则不因包含零阈值而降级。同理,系统评价制作者和指南制定者对相同估计值很可能会选择不同的阈值进行证据分级,最终导致对不精确性的判断不同。
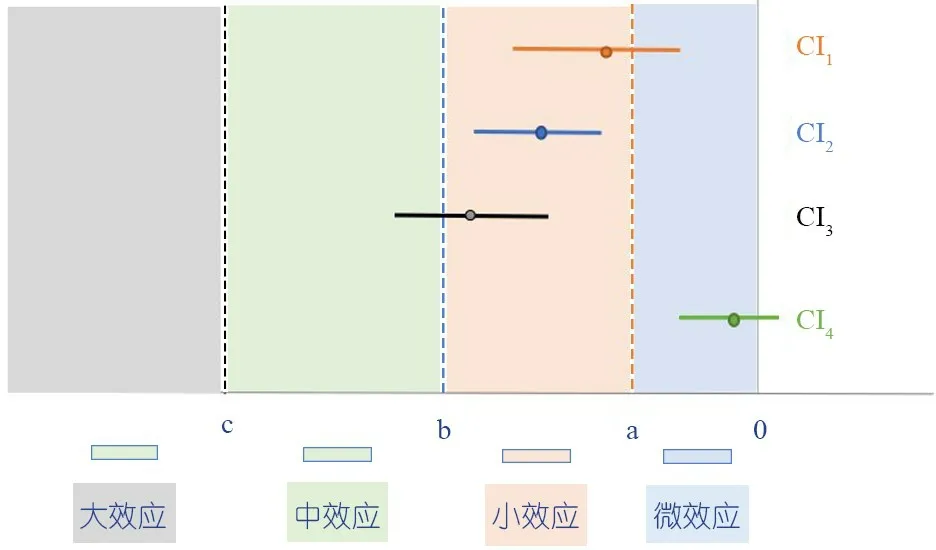
图1 效应量CI与阈值的关系
(3)考察研究样本量是否满足OIS。OIS是针对某具体问题而根据样本量的经典算法估算的所需研究对象人数,用于评估研究结果是否稳健。对于某一特定结局,当Meta分析纳入的样本量过小或结局事件数量少,即不满足OIS时, CIs将极不稳健,其位置会因增加少量数据而明显变动,故因不精确性降级。反之,意味着大量新证据不太可能使结果发生重大改变,不因不精确性而降级。
2.1 NMA不精确性的处理 对NMA证据分级遵从上述步骤和逻辑,但在考察OIS时有其特殊性,不同点在于:首先,以下两种情况无需考察OIS:①CI包含阈值,证据可信度因不精确性降低;②点估计值中等(如RR降低30%),且CI未包含阈值,则可推断样本量已经足够大,新证据不太可能推翻统计推断结论。其次,NMA效应量同时使用了直接证据和间接证据,因此不宜根据纳入的总样本量判断是否满足OIS,而通常需要估算NMA有效样本量(n),见表1。有效样本量是指忽略网状结构,也忽略直接证据和间接证据,将NMA估计量和CI看做单个研究的结果时,生成该效应量的等效样本量。第三,有时需要查看OR和RR的CI上、下界比值。

表1 考察OIS所用样本量信息
2.1.1 CI包含阈值时,根据不精确性降级 无论何种场景,当CI包含一个或多个阈值时,证据的可信度降级[2]。 当不精确性是唯一的降级考量时,考察CI的边界位置、包含多少个阈值,并按照GRADE指南[3]解释和评估降级后临床结论的恰当性。如果CI包含多个阈值,并且上、下界值分别代表了完全冲突对立的处理效应,如:下边界代表巨大获益,而上边界代表巨大的危害,则该结局所提供的信息量非常少。即便假定该证据体不存在其他严重问题,“可能获益”的结论也会存在误导,因此降3级,即证据可信度非常低[4],如此宽的CI常见于稀疏网状估计量[3]。
2.1.2 CI不包含阈值时,需查看NMA效应量大小 当相对效应大小适中(例如,相对风险降低或增加小于30%)时,并且CI较窄,不包含相关阈值,表明NMA估计值有足够的有效样本量,不需要因不精确而降级。
当CI过宽,不可能满足OIS,对于RR值,CI宽度可以用上、下界之比表示,比值>3时(OR值CI上、下界之比>2.5),则无论效应量大小、理论差异大小以及基线风险如何,均不可能满足OIS,则根据不精确性降2级。当CI特别宽,应考虑降3级[4]。
当CI很宽且不包含阈值,而点估计值很大且不太可信时,通常RR值95%CI上、下界比值<3,或在3左右(如:比值为2.7~3.3);对于OR值来讲该比值<2.5,或在2.5左右,无法直接降级,有必要评估NMA估计的有效样本量,并判断是否满足OIS,若不满足,只需因不精确性降1级。
对于连续变量结局指标,如均数差,无需根据CI界值给出降级结论,计算有效样本量并与OIS比较更为直观。
2.2 如何估算有效样本量和OIS 本文重要贡献在于给出了不同结局指标有效样本量的估算方法,并结合案例进行了实践模拟验证。
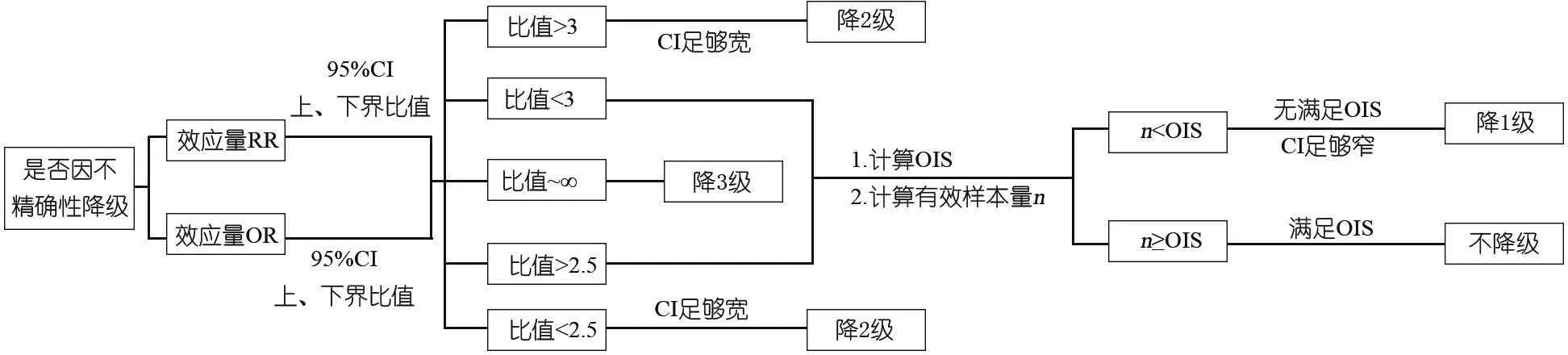
图2 根据RR值和OR值置信区间评估NMA不精确性降级决策路径
2.2.1 估计 NMA有效样本量 如前所述,若NMA估计量包含了直接证据和间接证据,只有当估计量与直接证据近似时,可以用纳入研究的总样本量估计NMA的有效样本量,否则要么低估了,要么高估了该估计量的有效样本量。作者根据结局指标不同(RR、OR或均值差)给出有效样本量的不同计算方法,本文将以RR值为例进行解读。有效样本量估算公式的推导基于3个基本假定和步骤:
(1)根据NMA估计量的CI上、下边界估算该指标的标准误:
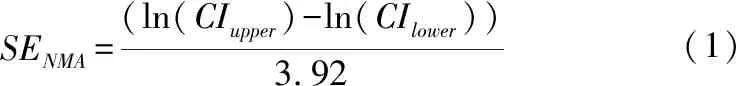
SENMA=(ln(CIupper)-ln(CIlower ))3.92(1)
(2)假定开展真实的两臂等样本研究,根据点估计值(RR、OR)、每组样本量、对照组结局发生率(Pc)、试验/观察组结局发生率(Pt)或合并标准差SD可以计算标准误(SEtrial),需注意计算过程中对RR值和OR值取以e为底的对数(ln):
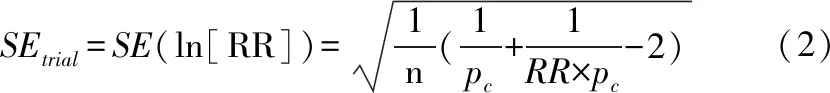
SEtrial=SE(ln[RR])=1n(1pc+1RR×pc-2)(2)
(3)假定NMA估计量来自于一个两臂等样本试验研究,另(1)和(2)中标准误对应相等,则可得到有效样本量公式:
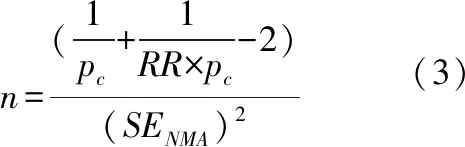
n=(1pc+1RR×pc-2)(SENMA)2(3)
2.2.2 估计OIS 虽然可信区间决定了研究的精度,但仍需考虑研究情境和相关预定阈值,根据估算有足够检验效能(如80%)的单个试验所需样本量OIS[5],基于不同场景和最小效应估算的OIS不同,导致相同的估计值不确定是否满足OIS[6]。因此,系统评价制作者选择生物学上合理的效应或最小重要差异,指南制定者基于全情境下的特定效应,将基于不同的OIS对不精确性做出不同的判断。
案例,关于预防龋齿疗效比较的NMA[7],1.23%的酸性磷酸盐氟化物(APF)凝胶与5%的氟化钠(NaF)清漆相比的RR值为0.67(95%CI:0.45-0.99),对照组龋齿合并风险(即基线风险)为77%。如果系统评价制定者认为RR降低33%这一效应量较大,则需要进一步评估NMA估计值有效样本量是否满足OIS,结果为:NMA估计的有效样本量(62)不满足OIS(184),因此根据不精确性而降级(表2)。

表2 有效样本量n和
2.3 其他考虑因素 当不精确性是由直接证据和间接证据之间严重不一致而产生的,只需对其中一个领域(不一致性或不精确性)降低评级[8],避免在不精确性方面重复降级。总之,NMA估计值的不精确处理须遵循与传统Meta分析相同的逻辑,也有其独特的考量角度,表3对文中案例降级判断给予了详细梳理。
3 主要启示和展望
NMA在干预性证据评价中有着重要价值,对其结果客观解读非常重要,GRADE证据评价可以推动我国临床研究者对NMA结论的整体认识,提高我国NMA研究的质量。
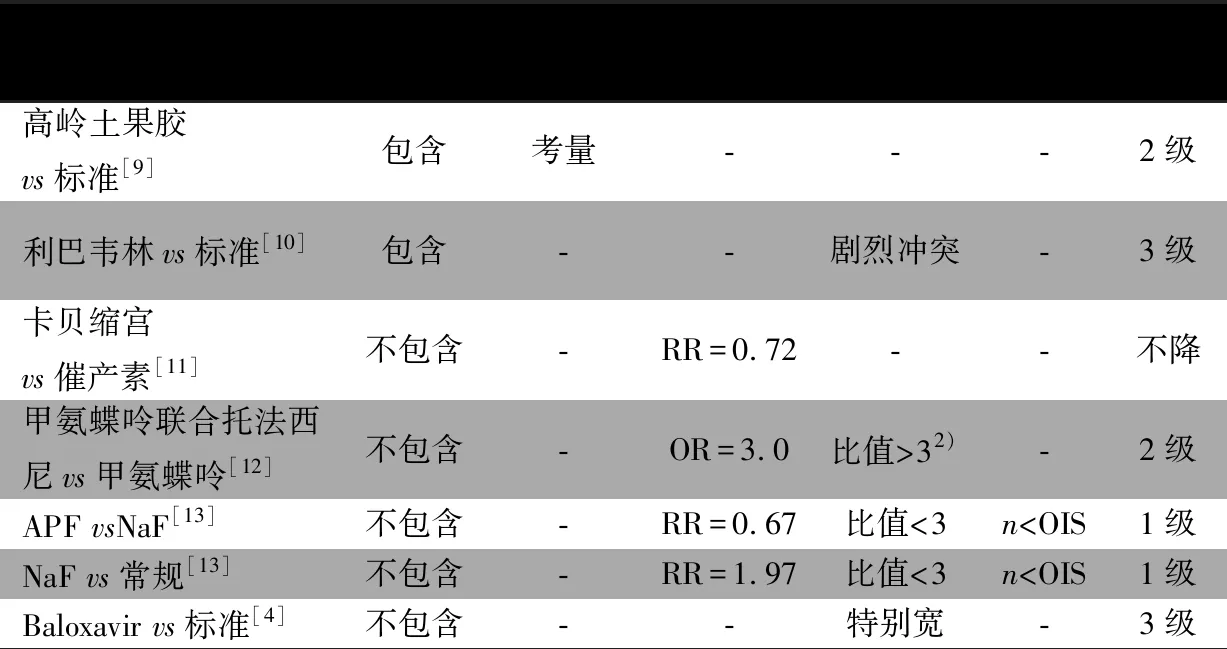
表3 案例梳理:NMA估计值不精确性处理相关因素1)
本次解读尽量结构化了关于NMA估计值不精确性评价的逻辑和方法,并对案例进行了全面梳理,但在实际制作系统评价和制定指南时,需要构建专业团队共同完成,以期为相关循证决策方提供有价值的决策依据。
