考虑气液混合流体时变特性的阀片式液压互联悬架建模*
2021-03-09谭博欢张邦基郭春杰
谭博欢,林 祥,张邦基,郭春杰,张 农,3
(1. 湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082;2. 博戈橡胶塑料(株洲)有限公司,株洲 412000;3. 合肥工业大学汽车与交通工程学院,合肥 230009)
前言
液压互联悬架是一种通过液压油传递压力、以惰性气体作为弹性介质、利用阻尼阀对油液的节流作用提供阻尼力的新型油气悬架[1]。它能够独立控制车轮相对车身特定的运动模态,因此能实现车辆的平顺性与操纵稳定性更好折衷[2-3]。
针对液压互联悬架系统,国内外学者及工程人员在动力学建模与分析领域开展了相关的研究[4-7],如周敏等[6]根据气体状态方程,建立液压系统单元数学模型;Ding 等[7]根据液压互联悬架系统的机械液压耦合边界条件,建立机械液压耦合系统动力学方程。但这些研究中为简化模型并提高计算效率,通常都做了一些假设,如将液压油视为不可压缩或具有固定流体特性的理想液体,将悬架系统阻尼阀简化为固定开口的节流孔等。
但在实际的工作过程中,液压互联悬架系统中的油液不可避免地会渗入气体,从而形成气液混合流体。随着液压缸中流体的压力不断变化,混合流体中的原始气体会不断被压缩/舒张,使流体的密度、体积弹性模量等物理性质具有时变特性[8-10],忽略混合流体物理性质的时变特性会对模型的准确度造成影响。
有别于传统减振器,液压互联悬架通常采用外置于液压缸的阀片式阻尼阀。阀片式阻尼阀通过叠加不同厚度与形状的阀片,改变预载荷等措施调节阀的节流特性,获得理想的阻尼特性[11]。阻尼阀是一个复杂的非线性部件,其阻尼特性受阀片厚度和变形量等多种因素影响[12]。因此将阻尼阀简化为固定开口节流孔的传统建模方法难以准确表征流体压力与阀片变形导致变开度间的相互作用。对此,有学者对阀片变形开展了研究[13-15]。Wang 等[15]提出了一种利用有限元方法求取修正系数以校正均布载荷作用下阀片变形方程的阻尼阀阀片堆变形量的工程估算模型。这一模型能较为准确地描述阀片变形量与压力之间的关系,但采用定常系数进行修正,难以准确描述变形量随半径变化的非线性关系。
本文中针对液压互联悬架系统,建立了考虑气液混合流体压缩时混合流体密度和体积弹性模量的时变特性的非线性数学模型,并提出一种非线性修正函数用以描述阀片变形量与半径间的非线性关系,针对同源单缸互联系统开展台架试验结果,验证提出的建模方法准确性,并讨论油气混合流体时变特性对系统特性的影响。
1 同源单缸互联悬架系统
互联悬架是指单个车轮运动导致其他车轮或车轮组弹簧力发生相应变化的悬架系统的总称[3]。液压互联悬架可以针对不同运动模式,配置悬架的阻尼与刚度,从而实现悬架刚度和阻尼的最优调节。图1 为抗侧倾双缸互联悬架,该系统由双作用液压缸、阻尼阀、管路、蓄能器等部件组成。当互联悬架两端同向跳动时,能够提供较大的阻尼力与较小的弹性力,异向跳动时能提供较大的抗侧倾刚度,因此在大多数工况都能保证车辆有较好的平顺性与操纵稳定性[4]。阀片式阻尼阀是决定悬架阻尼特性的关键元件,其阻尼力通过阀片对油液的节流效应而产生[15],阻尼阀物理构造如图2所示。

图1 抗侧倾双缸液压互联悬架系统

图2 阻尼阀物理构造
在对双缸互联悬架系统开展台架试验时,需要同时对两个液压缸进行作动控制,这对试验设备提出更高的要求。因此,需另辟蹊径寻求台架试验解决方案。图3 为单缸液压互联悬架系统示意图,该系统同样由液压缸、阻尼阀、管路、蓄能器等部件组成,与双缸互联悬架系统仅在互联方式上存在不同:单缸系统的上腔与自身的下腔相连;双缸系统的两缸上腔与彼此的下腔互连。可见,单缸系统与双缸互联系统具有相同的本构关系,且工作机理也相同,可以定义为同源系统。对于同源系统而言,建模原理和方法与双缸互联系统完全相同,因此,本文中针对这一同源单缸互联系统建立动力学模型,并开展台架试验研究。

图3 同源单缸互联悬架系统
2 单缸互联系统非线性模型
本文中考虑气液混合流体的时变特性和阻尼阀阀片变开度的影响,建立单缸互联系统非线性模型。
2.1 油液时变特性模型
液压互联悬架系统中,油液内含有少量空气,在时变流体压力的作用下,空气将与流体混合形成气液混合流体,从而使混合流体的密度与体积弹性模量呈现时变特性[8]。若忽略油液中气体的质量,压缩过程中气液混合流体的密度[16]可表示为

式中:ρh为理想液压油液密度;Vh0为混合流体中油液的初始体积;Vgt和Vht分别为混合流体中气体和油液的瞬时体积。
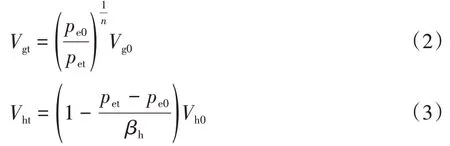
式中:pe0为初始平衡状态下流体压力;pet为动态过程中流体瞬时压力;Vg0和Vh0分别为混合流体中气体和油液的初始体积;βh为不包含空气的理想油液体积弹性模量。从而,混合流体中气体的时变体积分数可以表示为

式中:ς0为混合流体的初始体积分数,即ς0=Vg0/Vho;γ为气体多变指数,理想绝热状态下γ可取1.4,实际工作状态通常取1.2~1.3。
将式(2)~式(4)代入式(1)中可以得到混合流体时变密度与压力间的关系:
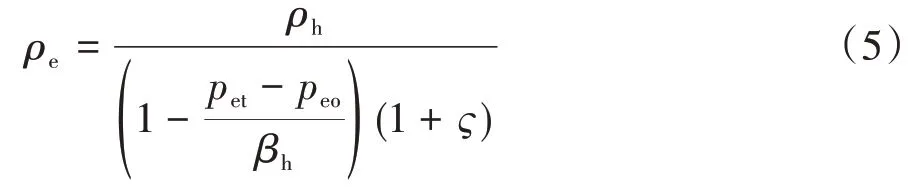
类似地,可以对混合流体体积弹性模量进行推导,从而得到体积弹性模量的计算公式为

2.2 阀片等效形变模型
基于圆形薄板弯曲变形理论,在极坐标下推导单个阀片的挠度ϑS与法向压力载荷pS之间的关系。根据弹性力学理论,阀片在如图4 所示的均布、连续压力下的弹性曲面方程在极坐标(rs,θs)下可表示为[17]
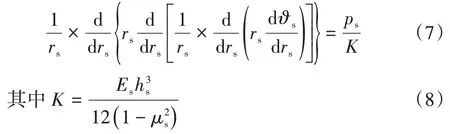
式中:K为单片圆形阀片的抗扰(弯曲)刚度;ES为阀片的弹性模量;hS为阀片的厚度;μs为泊松比。式(7)所示齐次微分方程的解可以表示为通解与特解的和:



式中:rf和rb分别为阀片外圆半径和内圆半径(见图4);hs为阀片的厚度或阀片堆的等效厚度(见图4)。

图4 单片环形阀片均匀分布压力载荷下的受力分析
将式(8)~式(16)进行恒等变形后可得

式(18)表达了均布载荷作用下阀片挠度与流体压力之间的关系。式中Cg为阀片变形系数,联立式(9)~式(18)展开可写为
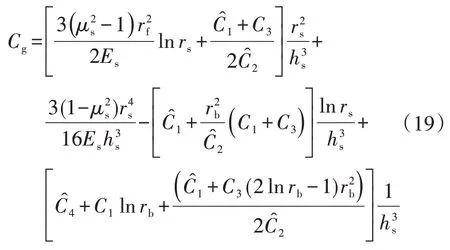
对于多片阀片堆砌而成的阀片堆,其等效厚度可定义为

式中h1、h2、h3、h4为各阀片的厚度。
从式(19)可见,阀片变形系数与阀片所受压力载荷无关,而与阀片材料属性(Es,μs)、阀片厚度hs和半径(rb,rf,rs)呈现复杂的非线性关系。这表明,阀片的变形与压力呈线性关系,而与半径呈非线性关系。而定常数的修正无法描述复杂载荷条件下阀片变形与半径之间的非线性关系。为此本文中在所推导的阀片变形方程基础上引入一个阀片形变非线性修正函数,校正载荷均布简化所带来的偏差,同时表达阀片变形与半径之间的非线性关系,其定义如下:
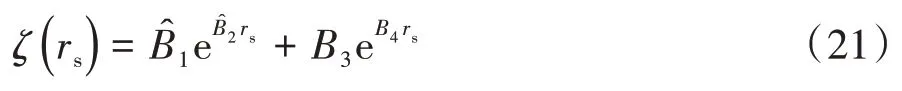

2.3 单缸系统流体力学模型
图3 描述了悬架跳动时系统内混合流体动力学变化关系。当活塞杆向上运动时,可定义液压缸无杆腔为压缩腔,有杆腔为伸张腔,不考虑温度变化对液压油动态特性的影响,由流体的可压缩性方程,可得液压缸压缩腔和伸张腔流量与压力之间的变化关系[10]:

式中:pi(i= c,r )为压缩腔或伸张腔的油液压力;Qi为压缩腔或伸张腔进出口的流出流入流量;Ac、Ar分别为活塞和活塞杆的截面积;ρi、βi分别为压缩腔或伸张腔内混合流体的时变密度和体积弹性模量,其值由式(5)和式(6)计算而得。Vcom和Vreb分别为压缩腔和伸张腔的体积变化量,可表达为

式中:Vc0和Vr0分别为压缩腔和伸张腔的初始体积;xh为活塞杆的位移。
活塞杆与液压缸的相对运动使压缩腔和伸张腔形成压差,这将促使油液从高压腔往低压腔产生泄漏,泄漏流量记为QL。泄漏量与压差呈线性关系[18],即

式中kq为泄漏中的压差系数。
忽略蓄能器中油液的可压缩性,已知蓄能器内油液压力与气体压力恒等,因此蓄能器油液压力与油液流量之间的关系[3]可以表示为

忽略油管的沿程损失与各接头处的流体压力损失,根据管路系统中流量处处相等可得
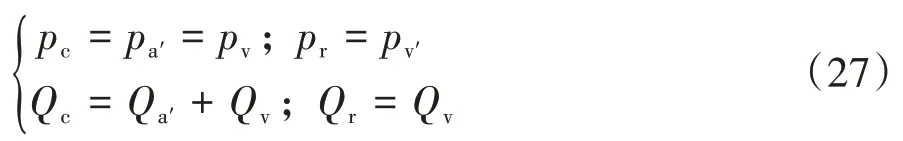
式中:Qc、Qr分别为由管路流至无杆腔、有杆腔的油液流量;Qv、Qa'分别为流经阻尼阀、蓄能器的油液流量;pc、pr分别为无杆腔、有杆腔的油液压力;pv'、pv分别为流经阻尼阀下端、上端的油液压力;pa'为蓄能器油液压力。
阻尼阀的节流特性取决于阀片的开度,即阀片变形量。基于式(22)阀片的变形方程可推导阻尼阀的流体力学方程,则压缩行程(ẋh≥ 0)阻尼阀的流量可表示为
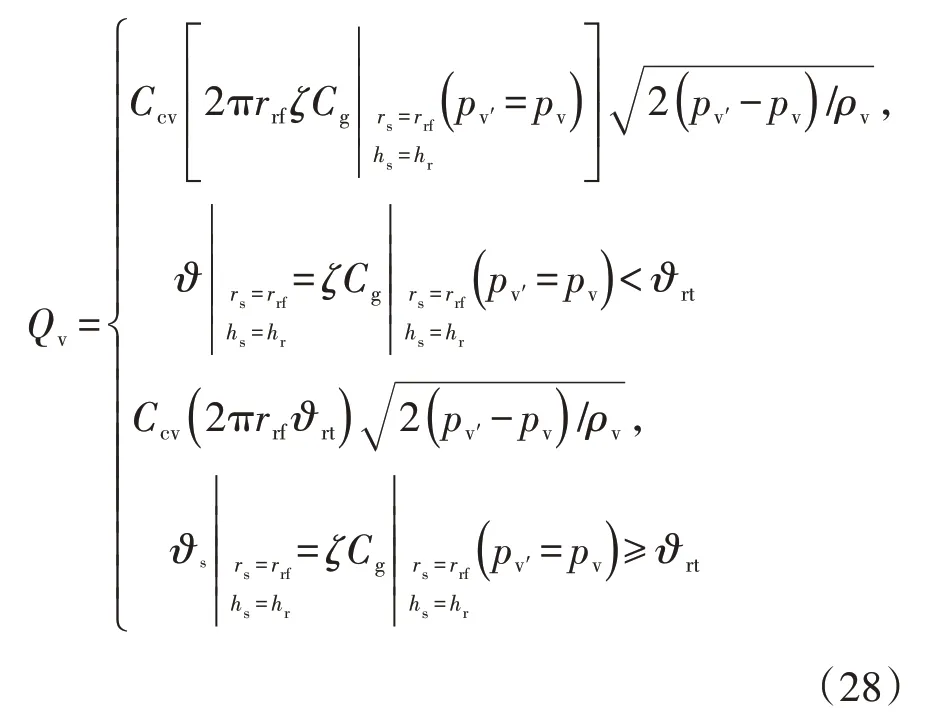
式中:Ccv为阻尼孔节流系数;rcf为压缩阀片边缘半径;hc为压缩阀片的等效厚度;pv和pv'分别为阻尼阀出入口压力(图3);ρv为油液密度;ϑct为压缩阀片变形的限位阈值,根据阀芯结构取ϑct=0.3 mm。同理,可推导拉伸行程流经阻尼阀的流量,选取拉伸阀片限位阈值ϑct=0.4 mm。限于篇幅,此处简略其公式推导。
联立式(23)~式(28)可求解系统的压力和流量。根据流体压力和液压缸运动的耦合关系,可得到液压缸输出力,即
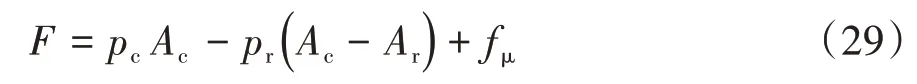
式中:Ac和Ar分别为活塞有效面积和活塞杆有效截面积;fμ为活塞与液压缸缸筒间摩擦力,主要由密封件引起。密封件与缸腔内壁间摩擦表现出黏滑、Stribeck 和迟滞效应。因此活塞的摩擦力可描述为库伦摩擦、Stribeck 摩擦和黏性摩擦的总和,且均是活塞运动速度的函数[19-20]:
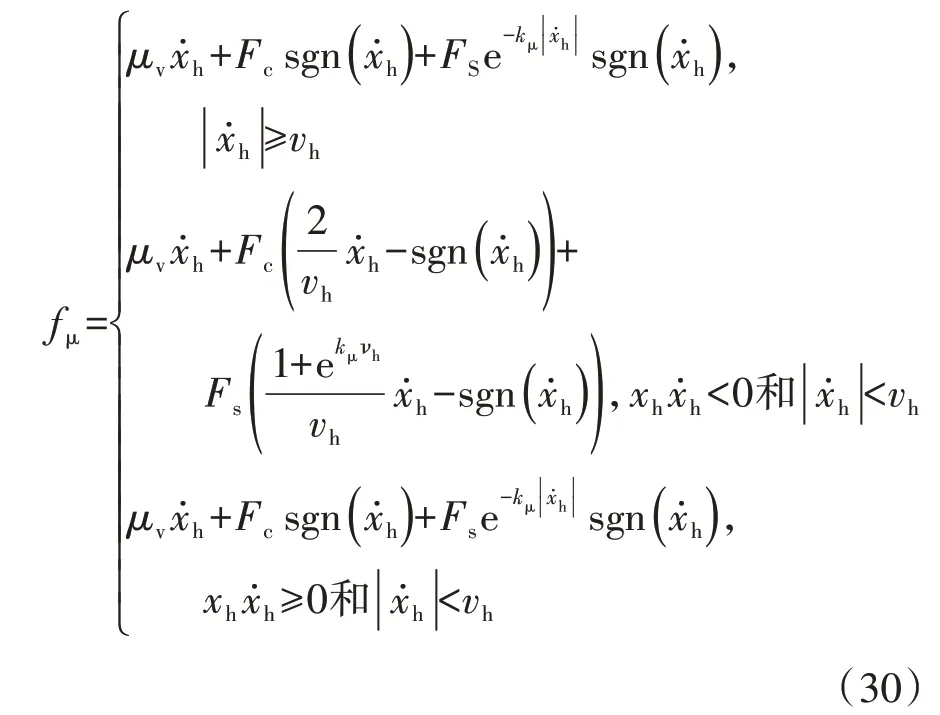
式中:μV为黏性摩擦系数;Fc为库伦摩擦力;Fs为静摩 擦 力 ;kμ为 Stribeck 系 数 ;vh为 迟 滞 临 界 转 换速度。
3 阀片形变参数识别
本文中采用有限元方法计算实际工况载荷下的阀片变形量,进而识别如式(21)所示的阀片变形非线性修正函数的待定系数。根据阀片在实际情况中受力情况,定义阀片的边界约束。由于三角垫片的限位,定义压缩阀阀片为三点式分散固定边界约束,内圈边缘定义连续固定边界约束;对于拉伸阀,将阀片内圈边缘定义为连续固定边界约束。结合阻尼阀阀芯结构,将阀片的载荷定义为单调递增压力,压缩阀和拉伸阀的载荷递增范围分别为[0.1,0.8]和[0.5,10]MPa。根据阀片的实际结构,定义阀片的弹性模量为2.12×1011Pa、密度为7 850 kg·m-3、泊松比为0.29,并进行有限元静态分析。图5 为通过有限元分析求解得到的阻尼阀阀片变形云图,由此可获得阀片在不同半径处最大形变量,并与2.2 节所建立的模型计算结果进行对比,辨识不同半径下的误差补偿系数ζˆ。本文中采用式(21)和式(22)拟合非线性修正函数辨识修正函数中的系数,辨识结果如表1所示。
针对本文中提出的包含非线性修正函数的阀片形变模型求解阀片变形位移等高线云图,并与有限元模型和文献[15]中的取定常数作为修正系数的模型进行对比,如图6 所示。图6 表明:引入阀片形变非线性修正函数后的模型计算结果与有限元分析结果高度吻合,能够等效描述实际工作状态下的阀片变形情况。这是因为非线性修正函数是以半径为自变量的函数,因此能够准确拟合阀片不同半径位置的变形量。而文献[15]方法采用定常系数进行修正,难以准确描述变形量随半径变化的非线性关系,因此在等高线图中与有限元结果表现出一定的差异。
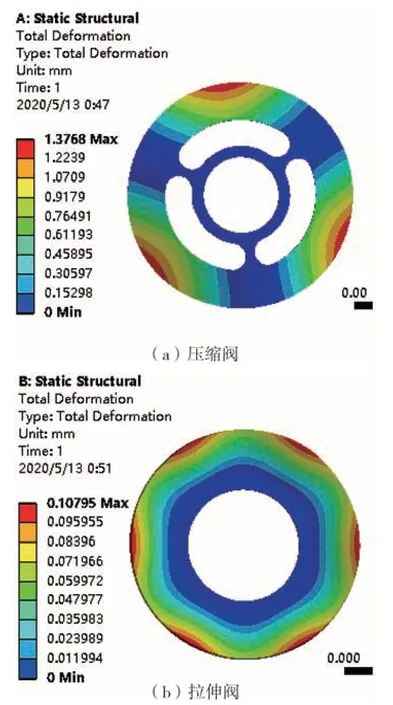
图5 阀片有限元变形云图

图6 阀片变形等高线云图

表1 阀片等效形变修正函数待定系数辨识
4 单缸互联系统仿真与验证
根据第2 节提出的建模方法建立考虑混合流体时变特性的单缸液压互联悬架系统数学模型,并识别阀片形变参数,将获得的模型与台架试验结果进行对比分析,以此验证建模方法正确性。同时,根据文献[3]和文献[21]中的未考虑混合流体性质的时变特性的传统建模方法,建立未考虑时变特性的单缸液压互联悬架模型。表2为数学模型物理参数。

表2 单缸互联系统理论模型物理参数
为验证所建立模型的准确性,针对单缸互联系统开展台架试验。按照汽车行业标准QC/T 545—1999《汽车筒式减振器台架试验方法》,搭建了单缸互联系统试验台架,如图7 所示。单缸互联系统按照图3进行搭建,其结构物理参数同样见表2。试验过程中,液压缸的动态输出力由MTS 试验机装载的力传感器进行采集,对应的加载位移和加载速度通过LVTD 位移传感器进行获取。选取正弦函数激励进行加载,加载幅值为50 mm,加载频率分别为0.16、0.41、0.83、1.24、1.66 Hz(对应的最大速度分别为0.05、0.13、0.26、0.39、0.52 m/s)。

图7 单缸互联悬架系统台架试验
图8和图9分别对比了理论模型(其中本文提出的考虑时变特性模型标记为“时变特性”,传统的模型标记为“时不变特性”)与台架试验动态输出力示功曲线与阻尼力曲线。观察图8 所示台架试验的示功曲线可以发现,台架试验与时变特性的示功曲线存在“回程”和“去程”关于平衡位置(位移为零)非对称的特性,其“回程”曲线段表现更为陡峭,而“去程”曲线段相对较为平缓,这是因为在液压缸被拉伸/压缩时,气液混合流体中的空气压缩/舒张,从而改变流体的物理性质,导致此种非对称性。压缩行程(去程)转变至拉伸行程(回程)后,有杆腔的流体压力由低向高攀升,导致气液混合流体中的气体被压缩且逐步溶解于液体中,最终到达饱和,因此气液混合物的密度和体积模量随着压力的升高而增加,并逐渐趋于恒定值(见式(5)和式(6))。此过程由于气液混合流体的特性改变致使图8 中左边曲线呈现“先缓后陡”趋势,而拉伸行程(去程)至压缩行程(回程)转变过程中去程压力变化较为缓慢,且混合流体溶解达到饱和状态,因此有别于图中左边曲线,右边曲线变化趋势较为平缓。这种变化趋势在图9 中也得到了印证。
图8 对比结果表明,由于本文提出的模型考虑了气液混合流体物理性质的时变特性,因此可以模拟示功曲线的非对称性,并能够更好地拟合试验曲线。而文献[3]和文献[21]中模型忽略了混合流体物理性质的时变特性,将流体密度、体积弹性模量和黏度系数视为定值,因此建立的模型得到的示功曲线关于平衡位置基本对称,这不符合实际系统的特性曲线,因此与试验结果出现了较为明显的偏差。

图8 单缸互联系统输出力示功曲线对比
图9 为阻尼特性曲线对比,结果表明台架试验的阻尼特性曲线中存在明显的迟滞现象,运动速度越大,曲线迟滞面积越大,这种曲线不重合现象与上述分析的非对称特性成因相同。此外,可以发现考虑时变特性曲线更符合试验结果,并能形成与试验曲线类似的迟滞。而时不变特性曲线结果在测试的速度范围内输出的阻尼力均高于试验结果,而且“回程”和“去程”曲线均与试验曲线存在较大的误差。由此可见采用本文提出的单缸液压互联悬架建模方法建立模型,与传统模型相比,能更准确反映实际情况下单缸液压互联悬架的动态特性。
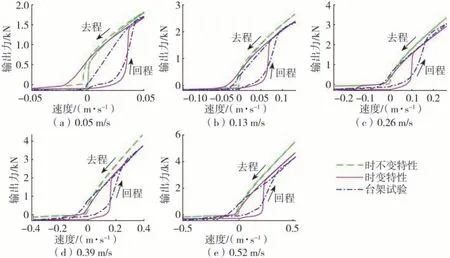
图9 单缸互联系统阻尼特性对比
5 结论
本文中考虑了液压互联悬架系统中气液混合流体物理性质具有时变特性,阻尼阀阀片变形量与阀片半径之间存在非线性关系的现象,建立单缸液压互联悬架系统非线性模型,并通过台架试验验证模型的准确性,本文中主要工作与得到的结论如下。
(1)推导了液压互联悬架中气液混合流体的时变特性模型,模型能够描述液压互联悬架系统中气液混合流体包括密度与体积弹性模量在内的物理性质的时变特性及对悬架特性的影响。
(2)提出一个阀片非线性形变修正函数,校正载荷均布简化带来的形变量的计算误差,并采用有限元方法识别修正函数系数。与有限元计算结果对比表明,相比于定常数修正因子,非线性形变修正函数的引入能更准确描述阀片形变与半径间非线性关系。
(3)气液混合流体在时变压力的作用下,流体中的气体不断被压缩或舒张,导致单缸液压互联悬架系统“输出力-速度”试验曲线出现明显的“迟滞”现象,且降低了阻尼力的峰值,这表明混合流体的时变特性会对悬架特性造成影响。
(4)与未考虑流体物理性质时变特性的模型相比,考虑时变特性的模型可以准确描述“迟滞”这一现象,且能更准确地拟合台架试验曲线。这表明本文模型能更准确地描述液压互联悬架的动态特性。
