考虑未知输入的主动悬架路面高程与等级识别研究*

丁仁凯，蒋 俞，汪若尘，刘 伟，孟祥鹏，孙泽宇

（1. 江苏大学汽车工程研究院，镇江 212013；2. 江苏大学汽车与交通工程学院，镇江 212013）

前言

路面作为外部激励源，直接影响主动悬架车辆的动力学性能（包括乘坐舒适性和行驶安全性）。对行驶路面信息进行识别能够为主动悬架控制提供准确、合理的先决条件，进而实现系统控制参数和工作模式的智能化切换。因此，实时感知路面信息对提高主动悬架控制系统性能有重要意义。

当前，对路面信息进行识别的方法主要可以分为3 类：直接测量法、非接触式测量法和基于车辆动力学响应的识别方法。直接测量法［1-4］须在车辆上安装路面不平度仪，并使其与地面保持接触，从而测得路面高程。该方法虽然测量精度较高，但无法应用到常规车辆进行车载实时测量，并且无法获得路面等级信息［5］。非接触式测量法［6-8］利用安装于车身上的各类传感器如激光传感器、超声波传感器扫描路面，直接测量路面高程。此方法识别精度较高，但成本高，且在复杂行驶环境下测量效果难以得到保证。基于车辆动力学响应的识别方法根据系统状态如车身加速度、车轮加速度间接获取路面高程信息［9-12］。该方法不需要借助额外的测量仪器或传感器，具有成本低、可移植性较高的优点，因此具有更广阔的研究前景。Uys 等［13］利用傅里叶变化进行路面高程功率谱密度分析，从而识别路面信息。Tudon‑Martinez［14］设计了 Y‑K 参数化的路面高程观测器，通过傅里叶变换由已获取的路面高程得到路面等级信息。顾亮等［15］通过车轮振动加速度信号对路面进行了识别。章新杰等［16］提出一种由悬架动行程信号区分路面等级的识别方法。

然而，现有依据车辆动力学响应估计路面高程信息进而识别路面等级，并以此对悬架进行控制的方法属于“慢切换”。而真实路面往往具有不确定性，如何在获取路面等级进行控制“慢切换”的同时，提取悬架瞬态响应，实现控制参数“快切换”，以提高悬架实时瞬态控制性能，目前鲜有研究涉及。总之，当前缺乏基于主动悬架车辆动力学响应的路面高程、等级和系统状态变量同时估计的方法研究。

针对上述路面识别方法的不足，本文中设计了考虑未知输入的主动悬架路面高程与悬架状态同时估计的方法和路面等级识别方法，从而为主动悬架工作模式/控制参数切换提供先决条件，实现各行驶工况下悬架系统综合控制性能最优。

1 主动悬架建模

选择1/4车辆线性模型作为研究对象，系统模型如图1 所示。根据牛顿第二定律，所建主动悬架模型的动力学微分方程可表示为

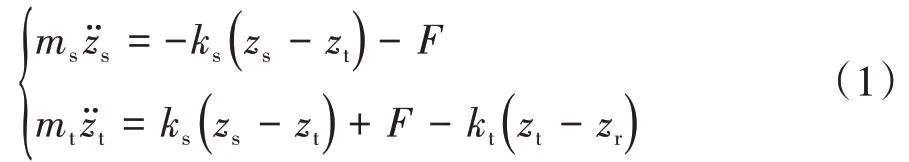
式中：ms为簧上质量；mt为簧下质量；ks为弹簧刚度；kt为轮胎刚度；F为悬架主动作用力。具体数值如表1所示。

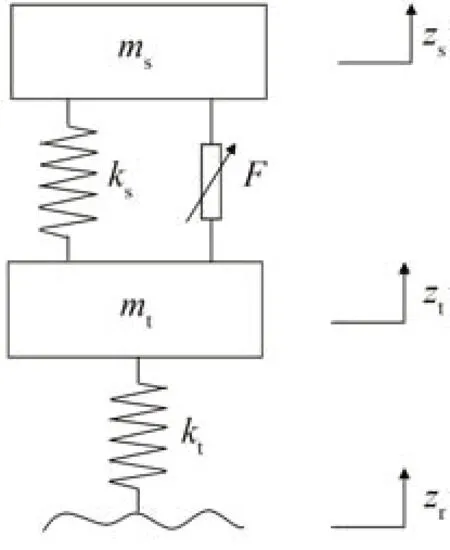
图1 主动悬架模型

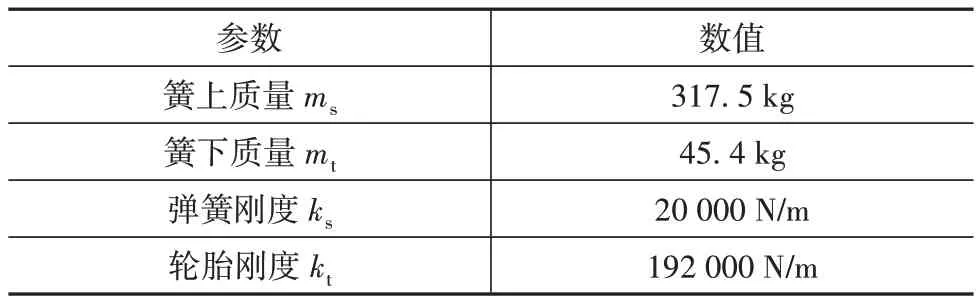
表1 1/4车辆模型参数

由文献［17］可知，主动悬架根据当前行驶工况进行适应性参数切换以达到预期控制目标，其切换条件可主要概括为两类：一是路面等级的变化，不同路面等级下，悬架整体性能需求有所不同，路面变化时悬架控制参数的切换即为慢切换；二是悬架瞬态响应的变化，真实路面激励下可能存在瞬态冲击，此时悬架瞬态响应随之变差，尤其是车轮动载荷（影响车辆行驶安全性），瞬态响应变化时的悬架控制参数切换即为快切换。因此，需要对路面等级和系统状态变量同时识别，而其首要条件是获取路面高程（位移）信息。

2 路面识别方法设计

2.1 路面高程估计

对主动悬架车辆的路面高程和悬架状态同时估计可归纳为含有未知输入（路面）的观测问题。传统观测方法是在明确当前系统状态变量的情况下对路面高程进行估计，或是在已知路面高程的情况下观测系统状态变量，其主要原因是因为路面高程与状态变量相互耦合。采用传统的单一观测器无法实现路面高程和系统状态变量的同时估计，因此本文中结合传统传感器获取理想作用力，实现状态变量与路面高程的解耦。

本文中提出一种考虑未知输入的卡尔曼滤波算法，对路面高程信息进行估计。对于式（1）所建立的1/4主动悬架系统，其状态方程可表示为

式中：w（t）为系统过程噪声；v（t）为测量噪声；A（t），B（t），C（t），D（t）为已知状态矩阵；X（t）为状态变量；U（t）为已知外部输入变量；Y（t）为测量变量。选取为状态变量，Y(t)=为测量变量。另外，为了区分可控作用力输入和路面输入，令U(t)=[F(t)]，U*(t)=[Zr(t)]，则系统离散控制方程可表示为

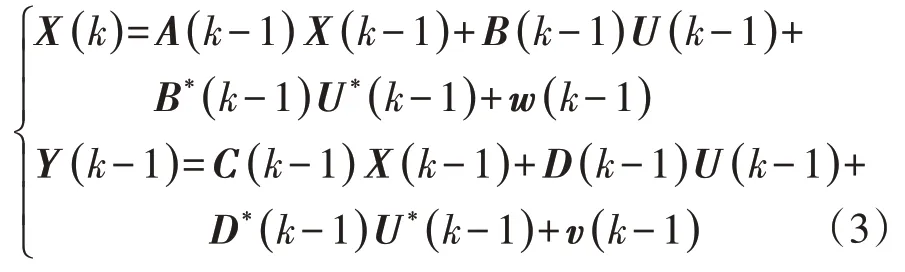
其中，假设w（k），v（k）为相互独立且服从正态分布的高斯白噪声，即：w（k）～N（0，Q（k））；v（k）～N（0，R（k））。其中，Q（k）为过程噪声的协方差，R（k）为测量噪声的协方差。

考虑未知输入的卡尔曼滤波算法［18］归纳如下。

状态估计时间更新：

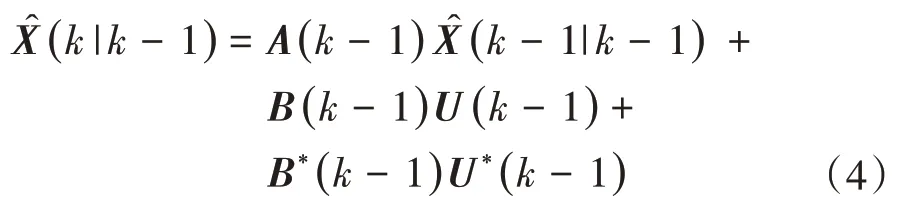
协方差矩阵时间更新：

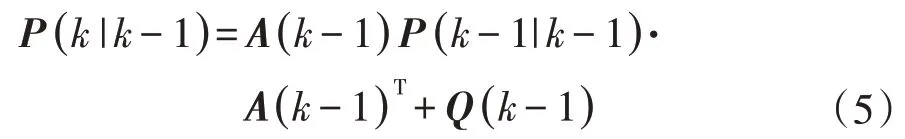
卡尔曼增益矩阵更新：

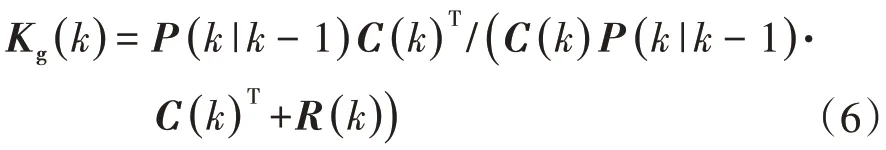
未知输入及其协方差估计：

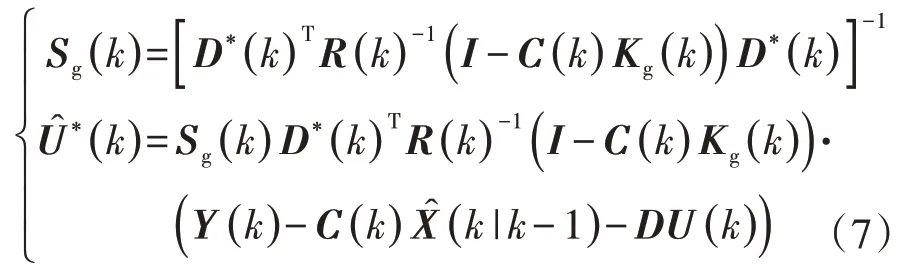
状态估计测量更新：

协方差矩阵测量更新：

根据式（7）可知，考虑未知输入的卡尔曼滤波对路面高程U*(k)进行估计的前提是已知理想作用力输入U(k)，U(k)由所采用的控制算法决定。本文中采用改进天棚控制算法［19］得到主动悬架理想控制力，并通过对车身/车轮加速度积分的方式获取理想改进天棚控制力需要的状态变量［20-21］。

估计出路面高程和车轮动位移后，可计算出瞬时车轮动载荷，这是进行“快切换”的先决条件。主动悬架的智能控制包括基于瞬态状态响应的“快切换”和基于路面等级的“慢切换”（见2.2 节）两部分，为使控制器在两部分之间合理切换，需要对“快切换”设定切换阈值。设定瞬态车轮动载荷超过车轮静载荷的4/5时，控制器进行“快切换”：

式中：Fdtl为估计的瞬态车轮动载荷；Fstat为车轮静载荷。另外，为了防止控制器频繁进行“快切换”，引入惯性环节：

式中τf≈0.007 s为时间常数。

2.2 路面等级分类

国际标准ISO/DID 8608给出了各路面等级分类标准，明确规定了各级路面不平度系数Gq（n0）的上/下限值和0.011 ～2.83 m-1空间频率范围内路面不平度均方根值qrms（σq）的上/下限值。因此，本文中将通过已获取的路面高程计算路面功率谱密度，再对路面功率谱密度进行积分，得到路面不平度均方根值，进一步提取兴趣频段内（0.011 ～ 2.83 m-1）的路面不平度均方根值（见图2），并依据等级分类标准实现路面等级分类。

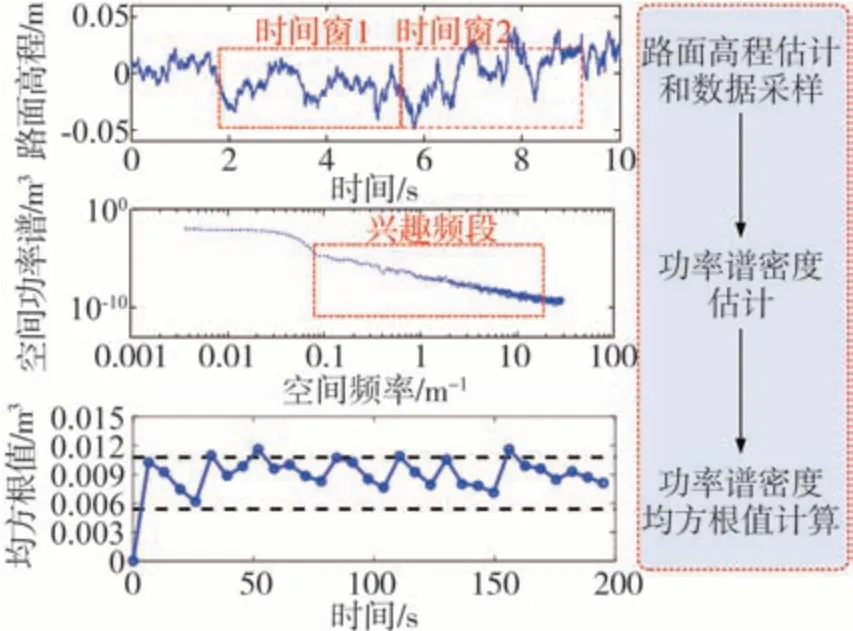
图2 路面等级分类原理

2.2.1 路面高程功率谱密度估计

采用AR 模型计算路面功率谱密度。假定随机序列x（n）可由线性差分方程表示的系统模型产生，即

式中w（n）为白噪声序列。对式（13）进行Z变换可得

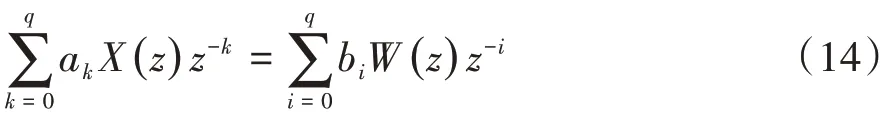
则系统传递函数可表示为

式中：z= ejw，则式（16）可简化为

由式（17）可知，当系数ak、bi和确定后，即可求解随机序列x（n）的功率谱密度。

当i＞1，bi=0时，式（10）可改写为

式（18）即 为 自 回 归 模 型 ，也 称 AR（Auto regressive）模型。对其进行Z变换可得

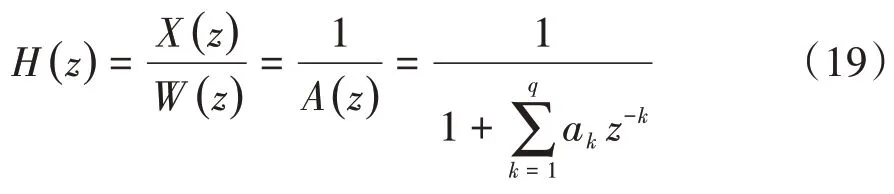
则AR模型的输出功率谱可表示为

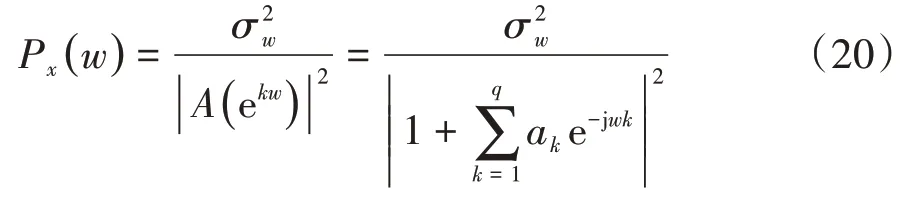
由式（17）可知，计算ak和就能够求解得到随机序列x（n）的功率谱密度。因此，采用AR 模型法进行功率谱密度估计的关键是模型参数估计。

设空间频域上的路面高程可表述为如式（21）所示的AR模型：

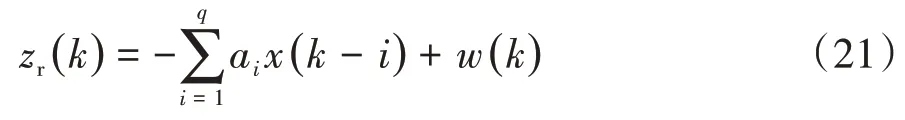
式中：ai为模型参数；w（k）为方差为的零均值平稳白噪声。

选取Burg 法进行模型参数估计，假设路面高程AR 模型的前向预测误差和后向预测误差分别为fp（k）和bp（k），即

式中：aps（s=1，2，…，p）为模型参数。

则前向预测误差和后向预测误差的功率之和可表示为

其中fp（k）和bp（k）的递推关系可表示为

式中：s=1，2，…，p，为模型阶次；hs为反射系数，并且有hs=ass，f0（k）=b0（k）=x（k）。

根据Burg法，使式（24）相对于反射系数hs最小，可得hs的估计值为

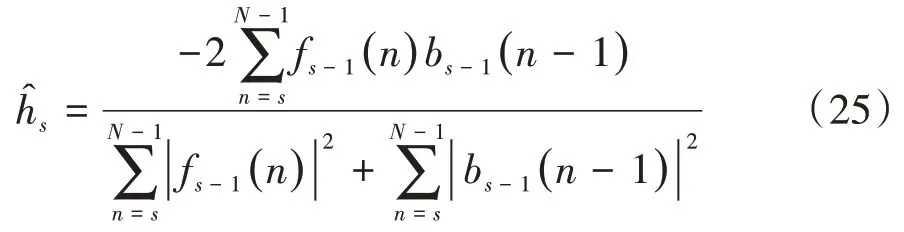
利用Levinson‑Durbin 递推算法可求得s阶次的AR模型的参数：

2.2.2 路面高程功率谱密度均方根值计算

实现路面等级分类还需要根据路面功率谱密度估计结果，计算0.011 ～2.83 m-1空间频率范围内的功率谱密度均方根值。而路面高程功率谱密度均方根值的计算可转化为对路面功率谱密度曲线下不规则图形面积的求解过程。另外，由AR 模型估计出的路面功率谱密度是时间频域的，因此，须结合行驶车速将所得路面时域高程功率谱密度均方根值转换到空间频域。短时间内，假设车速恒定不变。由此，提出了一种如式（27）所示的用于离散信号的功率谱密度均方根值计算方法。

式中：u为行驶车速；0 和j分别对应上截止频率（fL/nL）和下截止频率（fU/nU）的数据编号；f（x）为数据x对应的时间频率；Gq（f（x））为时间频率f（x）对应的路面功率谱密度。

采样时间（时间窗口）是决定路面等级识别精度的关键所在。本文中在选取一定时间窗口内的路面高程样本数据后，采用AR 模型估计其功率谱密度，再通过式（27）和式（28）计算兴趣频段内路面高程功率谱密度均方根值。时间窗口长度对路面高程功率谱密度均方根值估计精度的影响如图3 所示。时间窗口选取越长，样本数据越多，估计误差越小，但计算时间随之增加，即系统响应时间增加，反之相反。

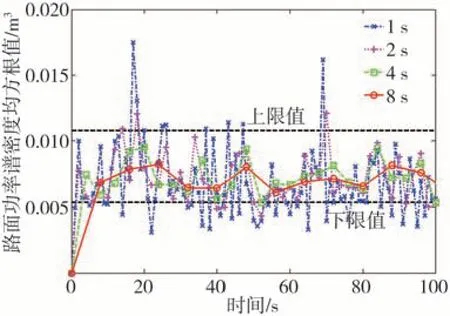
图3 时间窗口长度对估计精度的影响

为了协调系统响应时间与估计精度之间的矛盾，提出正确率评价指标来衡量估计精度的高低，其表达式为

式中：P为某时间窗口下超过实际路面高程均方根值限值的估计点数；N为路面高程均方根值估计总点数。图4 为B、C 和D 3 种等级路面下估计正确率随时间窗口长度的变化关系。可以看出，超过某一时间窗口长度后，其正确率无法得到有效提高，因此，确定时间窗口长度为6.5 s。

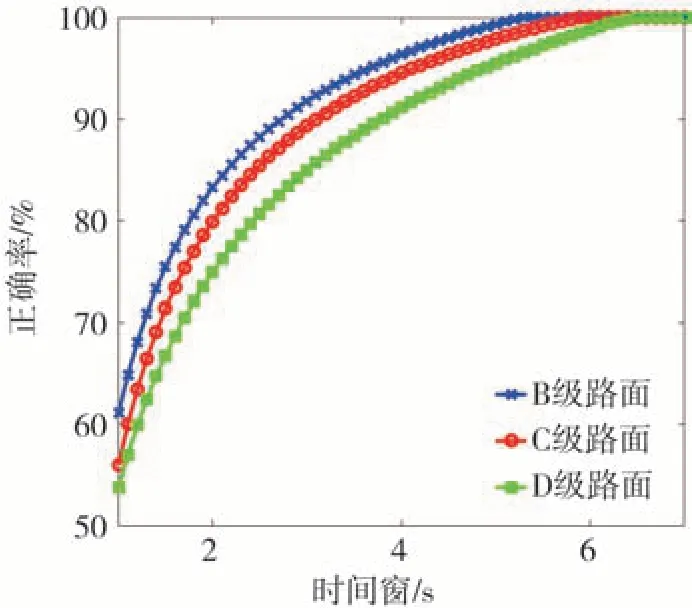
图4 估计正确率随时间窗口长度的变化趋势

3 仿真分析

车辆实际行驶过程中，路面等级、行驶车速和悬架控制参数始终在发生变化。因此，出于实际考虑，需进行路面等级、行驶车速和控制参数对路面高程和等级分类估计精度的影响分析，主要设置3 种仿真工况（参数见表2）：工况一是同一行驶路面下不同行驶车速（此时控制参数保持不变）；工况二是同一行驶路面下不同控制参数（此时行驶车速保持不变）；工况三是不同行驶路面下不同行驶车速与不同控制参数。

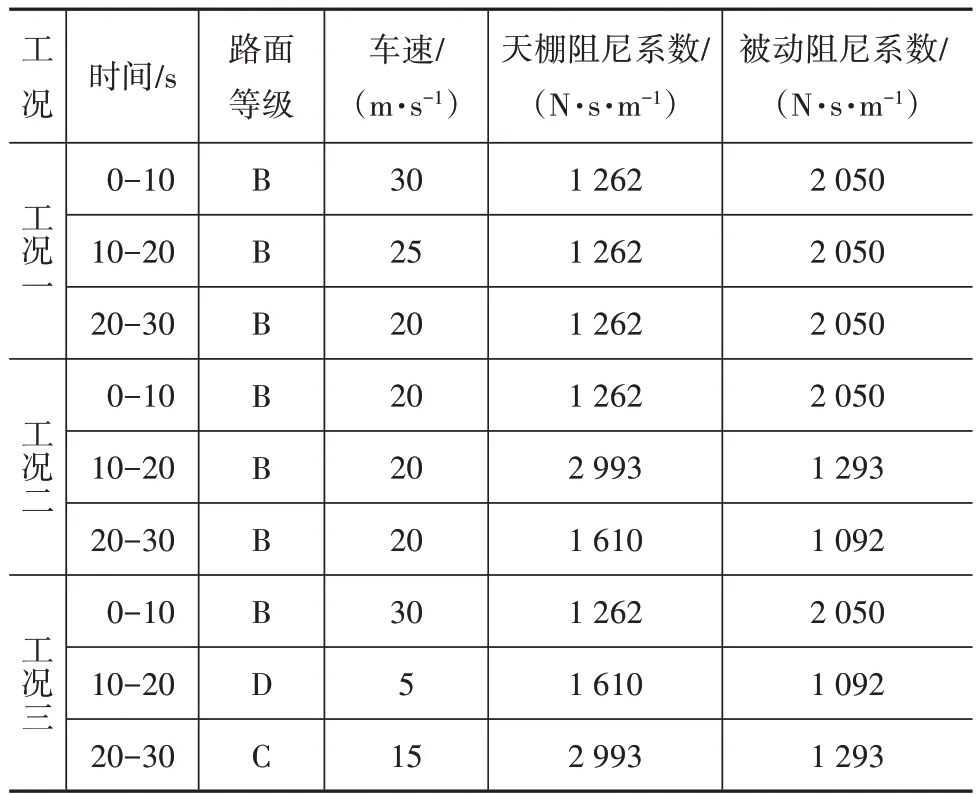
表2 3种仿真工况参数

3.1 路面高程估计方法验证

根据2.1 所述考虑未知输入的卡尔曼滤波算法，首先对系统初始值Q、R矩阵进行赋值：

为了更加准确地体现真实行驶路面，并检验所设计路面高程估计方法对瞬态性能的提取效果，在路面输入中加入了离散冲击信号，图5～图7 分别给出了3 种工况下的路面高程和车轮动位移估计结果。从图中可以看出，本文所提出的路面高程估计方法在各行驶工况下均能较为准确地跟踪实际路面高程和车轮动位移，从而为主动悬架的快切换提供了正确的判别条件。

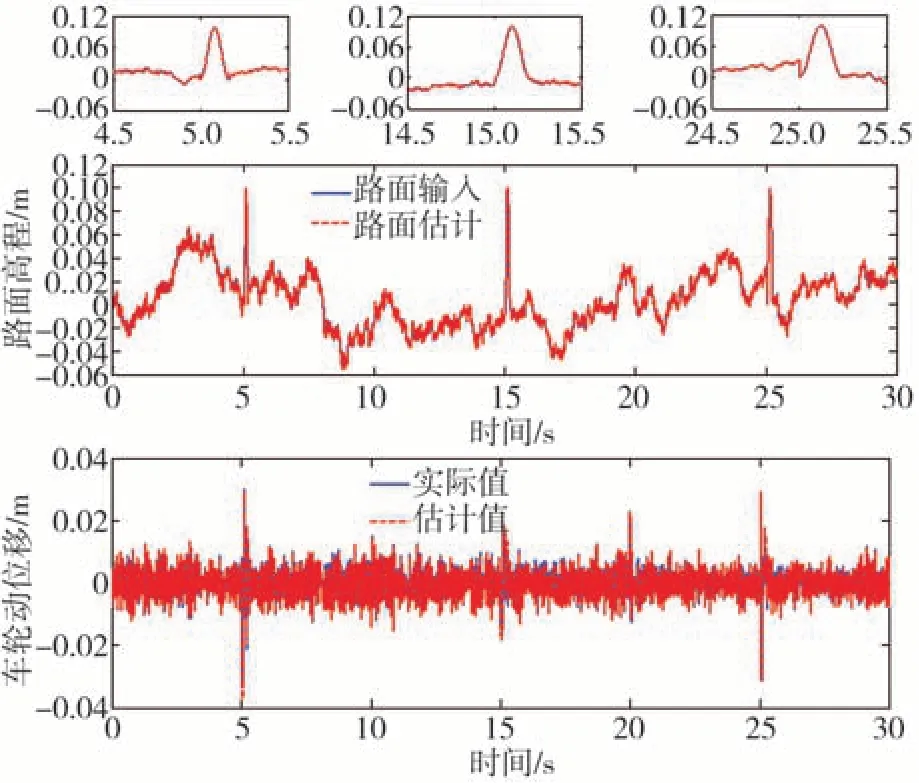
图5 工况一下路面高程与状态变量估计结果

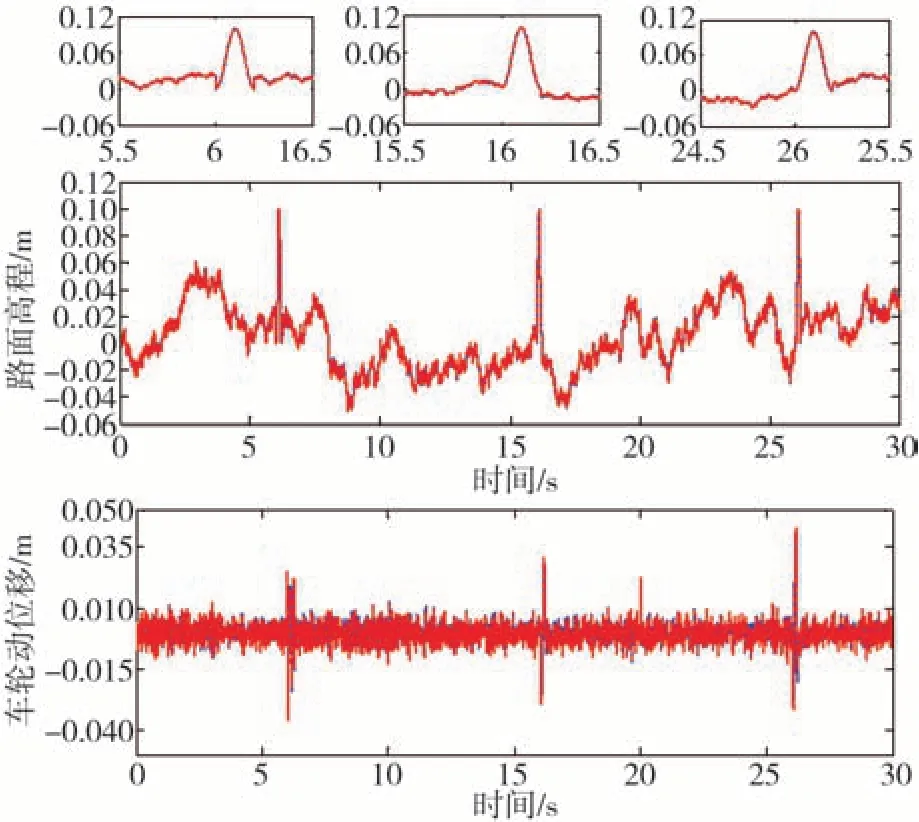
图6 工况二下路面高程与状态变量估计结果

图7 工况三下路面高程与状态变量估计结果

3.2 路面等级分类方法验证

图8～图10 给出了3 种工况下对路面高程、路面功率谱密度和路面等级的估计结果。为验证路面等级分类效果，路面输入未加入离散冲击信号。同时需要说明的是，由于路面等级并不会频繁变化，为了更加接近真实情况，增加了不同等级路面的仿真时长，即本节所设置的仿真时间与表2 是不同的。从图中可以看出，无论行驶车速、控制参数和路面等级如何变化，路面高程、路面功率谱密度都具有较高的估计精度，且所计算出的路面功率谱密度均方根值都分布在所对应路面等级均方根值的上下限值之间，由此可以准确地判断出路面等级。值得注意的是，当路面等级突然发生改变，由于存在一定的系统时滞，此时无法立即判断出路面等级（见图8）。

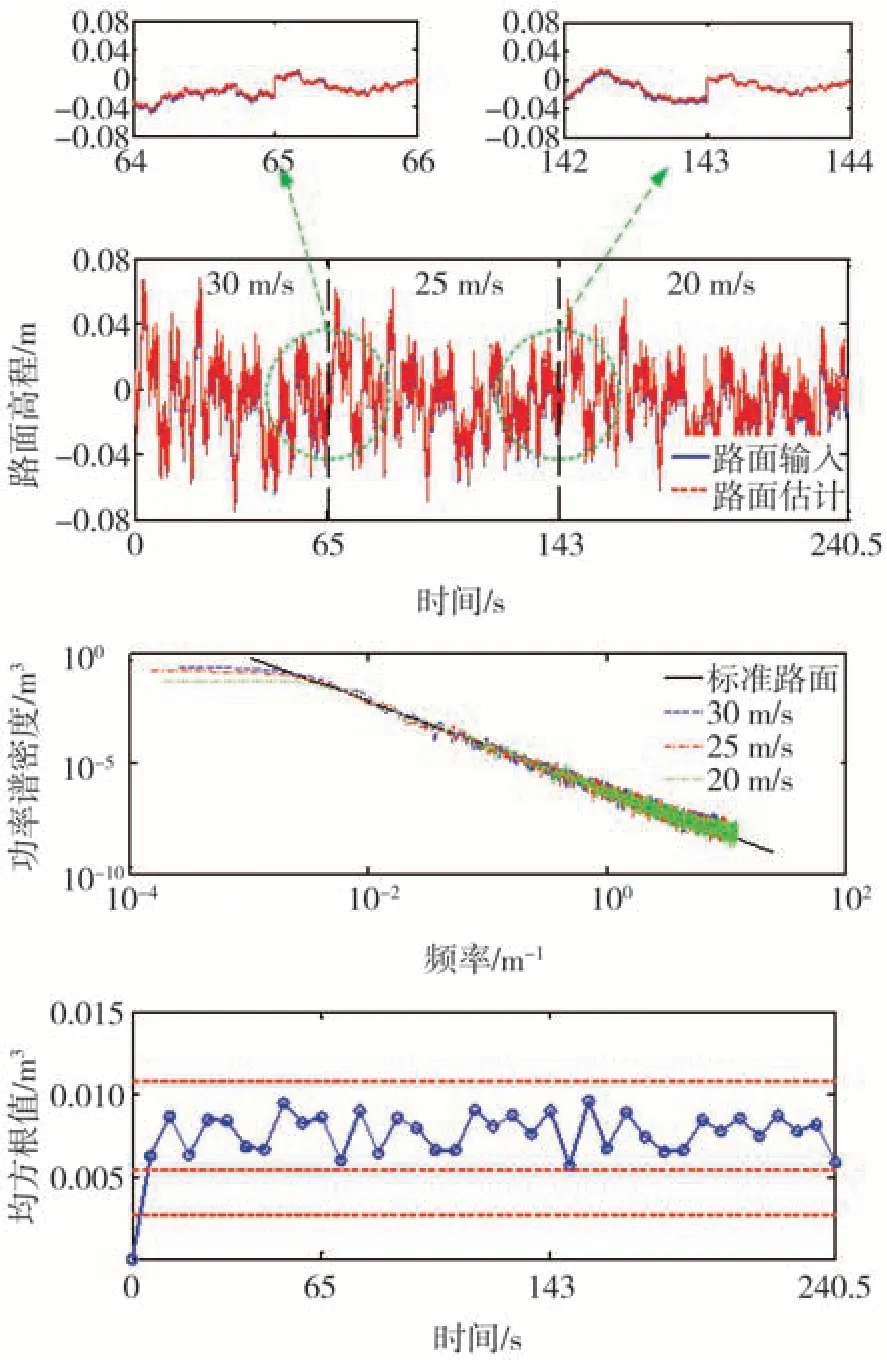
图8 工况一下路面等级估计结果

上述仿真结果表明，行驶过程中的“行驶变量”包括车速、控制参数和路面等级并不会影响对路面高程、悬架状态、路面功率谱密度和路面等级的估计精度。因此，上述仿真结果验证了本文中提出的路面高程和路面等级估计方法的正确性。

图9 工况二下路面等级估计结果

4 台架试验

搭建的主动悬架路面高程/等级识别控制系统如图11 所示。根据前文分析，控制参数的变化并不会影响路面高程/等级的估计结果，因此测试中控制参数不变。测试台架各模块功能如下：

图10 工况三下路面等级估计结果

（1）上位机建立悬架模型，定义仿真工况，监测仿真状态；

（2）dSPACE 用于运行悬架模型，传递悬架状态信号到控制器；

（3）控制器采用基于D2P（Development to proto‑type）的快速开发原型控制器，运行控制算法，输出控制信号到直线电机/磁流变阻尼器驱动器；

图11 路面高程/等级识别控制系统

（4）驱动器接收来自控制器的控制电压信号（PWM），驱动直线电机/磁流变阻尼器；

（5）INSTRON 8800 数控液压伺服激振台用于模拟悬架位移，并将作动器作用力信号反馈给dSPACE。

试验过程中采用图12所示的包含3种路面等级（B、D、C）的混合路面作为激励输入，3种等级路面下的行驶车速分别为20、5和10 m/s。

图12 混合路面激励输入

图13 和图14 为路面高程和路面功率谱密度估计结果。从图中可以看出，所设计路面识别方法对混合路面高程和功率谱密度都有较高的估计精度，并在此基础上计算出相应功率谱密度均方根值，进一步根据所得均方根根值进行路面等级识别（见图15）。从图15 中可以看出，识别的路面等级从整体来说与实际路面等级是一致的，但偶尔会存在误判的情况。此外，所设计路面高程/等级识别方法能够同时准确地估计出车轮动位移（见图16），由此，可实时监测悬架瞬态动载。

上述试验结果验证了路面高程/等级和系统状态变量估计方法的可行性和有效性，尽管路面等级识别偶尔出现误判的情况，但从整体估计效果来看，路面高程和车轮动位移估计精度达到90%以上，3种等级路面的估计精度达到了85%以上。由此说明，本文中提出的路面高程/等级和系统状态变量估计方法是可行且有效的。

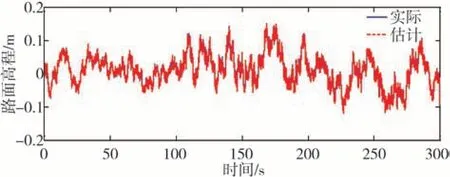
图13 路面高程估计

图14 功率谱密度估计

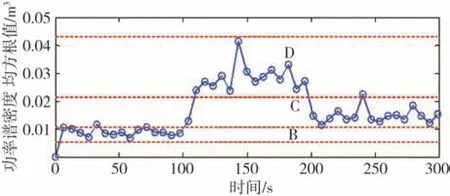
图15 均方根值计算

图16 车轮动位移估计

5 结论

本文中提出了一种结合传感器信息，采用考虑未知输入的卡尔曼观测器对路面高程和悬架状态同时进行估计的方法。基于获取的路面高程信息，利用AR 模型估计路面功率谱密度并计算其均方根值，进而对路面等级进行实时分类。仿真和试验表明，车辆行驶过程中的“行驶变量”（车速、控制参数和路面等级）不影响路面高程、悬架状态、路面功率谱密度和路面等级的估计精度。路面高程和车轮动位移估计精度均达到90%以上，路面等级识别精度达到85%以上。验证了提出的路面高程与等级识别方法的正确性和有效性，为实现主动悬架智能“快-慢”切换控制提供了理论基础。