模拟电路实验拓展之——混沌电路

秦玉娇，张新国

(1.曲阜师范大学实验教学与设备管理中心，山东 日照，276825；2.兰州大学信息科学与工程学院，甘肃 兰州，730000)

1 引言

模拟电路实验是电子类专业学生学习专业实验课程的基础，但教师在基础实验教学过程中，基本流于形式，对学生动手能力、观察能力和创新能力的培养略显不足。本文结合混沌系统理论特点，特将混沌电路引入到模拟电路实验的讲授中，作为模拟电路实验的拓展型实验。

混沌是20 世纪七十年代出现的重要理论，正如福特所说：“相对论消除了绝对时间、空间的臆断;量子力学消除了关于可控测量过程的牛顿式虚梦;而混沌则消除了拉普拉斯关于确定论式可预测性的幻想。”施莱辛格说：“二十世纪科学让人永远铭记的只有三件事，那就是相对论、量子力学和混沌学。”

混沌行为存在于许多自然系统中，如天气和气候。它也自发地发生在一些带有人造部件的系统中，例如道路交通。这些行为可以通过分析混沌数学模型或通过分析技术来研究。混沌理论在很多学科中都有应用，包括气象学，人类学，社会学，物理学，环境科学，计算机科学，工程学，经济学，生物学，生态学和哲学等。该理论形成了复杂动力系统，是混沌理论边界和自组装过程等研究领域的基础[1]。随着信息技术地不断发展，保密性需求不断提高，我们可以借助实验室电子线路模拟混沌现象，对实际问题进行理论分析，不断设计更符合实际现象的理论模型，进而对工程技术领域给出较为准确的预测。目前研究比较多的是蔡氏电路。

2 混沌电路原理及组成元件

2.1 混沌电路原理

混沌电路是一个由确定性运动方程所描述的确定性电路，由直流或确定性输入信号激励。产生混沌信号的方法主要包括：时间延迟、扰动输入、复杂系统。而针对混沌电路，其关键在于状态方程，且该方程应为自洽的，参数满足产生混沌的条件。在混沌理论分析的基础上，将状态方程中理论参数通过对应关系变换（比例变换、微分-积分变换、加减法变换等），最终将理论参数值转换为所需要的电路参数值，实现理论指导实践，设计混沌电路，验证混沌吸引子存在的可行性。

2.2 混沌电路基本组成原件

由于混沌理论属于非线性科学，组成混沌电路的元件一定包含非线性元件，主要为非线性电阻、非线性电容、非线性电感和运算放大器，其中运算放大器的基本单元有反向放大器、反向积分器、反相加法积分器等，见图1。所以弄清基本元件在非线性电路中的应用对于指导混沌电路设计至关重要。

图1 反向放大器、反向积分器、反向加法积分器

2.3 具体混沌电路实例

见图2 所示，这是一个具体的混沌电路，没有频谱要求，各个元件数值已在图中标注。混沌电路由6 个运算放大器A1-A6 构成，A3、A5、A6 是积分器，分别输出x、y、z，A2、A4 线性放大器，A1 是限幅非线性放大器。电路输出x、y、z 是与蔡氏电路完全相同的波形，但没有电感器，称为无电感蔡氏电路。

图2 优化的无电感蔡氏电路原理图

由电路图和改进的蔡氏电路方程[2]

可知电路状态方程是：

其中，表达式（2）中的参数并不是唯一的，此处为了表达的方便从实验中选取最优值α=10,β=13.24,α2=2.56,α3=4。f(x)是非线性部分

3 实验结果与分析

3.1 具体混沌电路仿真结果

电路运行结果的传统方法是搭建电路，使用示波器调试、测量很麻烦。在这里使用的软件有EWB、MultiSim、Matlab 等，使用EWB 软件仿真本电路的运行结果如图3 所示。注意图3 中z 输出端有一个附加的电路很重要，没有这一附加电路，混沌振荡无法开始。

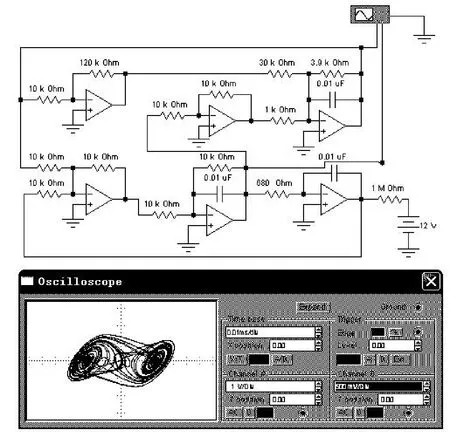
图3 EWB 仿真方法与结果

本电路已经经过物理电路实验验证，实验结果如图4、图5所示，是使用示波器测量，用照相机拍摄的照片。图2混沌电路有3个输出点，输出3个电压变量x、y、z，时序波形图如图4所示。分别将电压变量x、y、z其中的2个加到示波器的2个信号测量端，并将示波器工作方式置于李萨茹方式，结果称为相图，如图5所示。并且还得到当α取不同值时，V1-V2相图的演变关系，图6所示。

图4 物理电路输出的时序波形图

图5 物理电路输出的相图

图6 相图演变

3.2 结果分析

从可视化相图分析，变量与变量之间随着时间演化形成双旋涡模型，围绕两个吸引子来回游走，但是并不会相遇，符合混沌系统发生电路特点，是一个三维混沌系统信号发生电路。并且该电路元件种类较少，搭建比较容易，优于传统蔡氏电路。

4 结论

由混沌发生电路最基本的组成元件入手，层层引入，用一种简单明了的方式提出混沌电路，通过电路状态方程的确定、方程的数值计算以及数据处理，有效考察了编程能力、数值分析能力和逻辑思维能力，优化模拟电子技术教学内容，不断培育学生的创新能力。演示混沌效应同时，增强学生对于混沌内容的理解。