EAST上低漂移差分积分器的研制

王 勇，季振山，刘广君，王 枫

(中国科学院 等离子体物理研究所，安徽 合肥 230031)

在磁约束领域，托卡马克装置是最有可能实现受控核聚变的装置之一。先进超导托卡马克实验装置(EAST)[1-2]是中国科学院等离子体物理研究所自主研制的全超导非圆截面托卡马克核聚变实验装置，其设计目标是实现1 000 s等离子体放电。在托卡马克放电实验过程中进行等离子体反演时，要用到单匝环测量的极向磁通值[3]。单匝环信号测量有两种方法，一种为绝对测量法，该法对每个单匝环信号单独积分，在程序中将其他单匝环积分信号减去参考单匝环1的积分信号后用于计算控制；一种为相对测量法[4]，该法直接在单匝环信号源上扣除参考信号，将单匝环1作为参考，其他单匝环信号与其相减，再由积分器进行积分，然后进行反演计算。相对测量法的好处是可在信号源端直接去掉参考信号产生的磁通值，仅考虑相对变化量，这样即可用积分时间常数相对较小的积分器实现单匝环信号的测量，从而提高信号的信噪比。

单匝环感应到的是微分量，欲还原该信号，需使用积分器[5-8]。传统的模拟积分器均为单端输入形式，对共模信号基本无抑制能力，共模信号会被当作有效信号而积分，长时间积分会导致积分误差很大。而采用相对测量法时，参考单匝环会与其他单匝环相连并连接到后端的积分器，这种连接方式会形成很多地环路[9]，从而引入共模干扰。为较好地抑制共模信号对积分结果的影响，需采用差分输入形式的积分器。对于存在共模电压的电磁测量环境，差分积分器将对提高测量精度大有帮助。

本文拟通过分析差分积分器的工作原理，设计一具有高共模抑制能力的积分器，以提高单匝环相对测量的精度。

1 差分积分器设计

EAST有较完整的电磁测量系统，并有配套的积分测量系统[5]，之前使用的积分器均为单端输入，本工作将原积分测量系统中的单端积分器换为差分输入形式。

1.1 差分积分器原理

差分积分器与标准差分放大器类似[10]，仅将其中的两个电阻更换为电容，如图1所示。

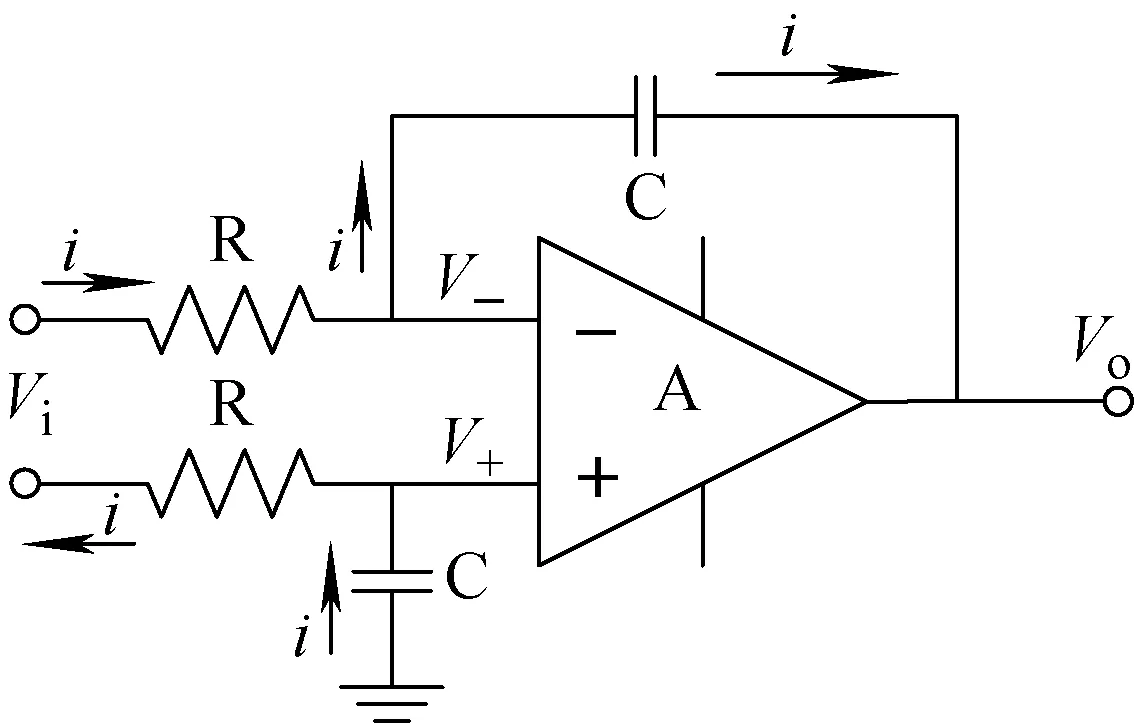
图1 差分积分器原理

由虚地原理可知：V-=V+，则流经电阻R的电流为：i=Vi/2R。

设电容C上的初始电压为0，且从零时刻开始积分，则有：

(1)

(2)

(3)

式中：V-为运放A负向输入端电压；V+为运放A正向输入端电压；Vi为差分积分器输入电压；Vo为差分积分器输出电压。

因此，差分积分器与单端积分器的功能相同，但在抑制共模信号方面有区别。图2为差分积分器抑制共模信号示意图。

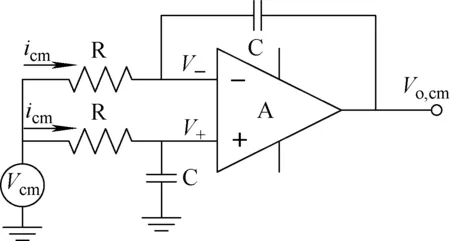
图2 差分积分器抑制共模信号示意图

假设输入端的共模电压为Vcm，由于V-=V+，则流经两个电阻R的电流相同，均为icm，则有：

(4)

(5)

由此可见，差分积分器对共模信号起到了很好的抑制作用。实际工作中，共模抑制效果还受电阻、电容的不一致性以及运放的影响。

1.2 差分积分器调零电路

差分积分器中运算放大器的“+”和“-”输入端电位均会随输入信号的变化而变化，很难直接用于调节积分漂移。而单端积分器存在“虚地”，可较方便地调节其漂移。因此，通过电阻分压的方式调节单端积分器的积分漂移输出，将它与差分积分器的输出由后端的仪表放大器相减，输出结果可持续抑制差分积分器的积分漂移，从而实现差分积分器调节积分漂移的目的，如图3所示。

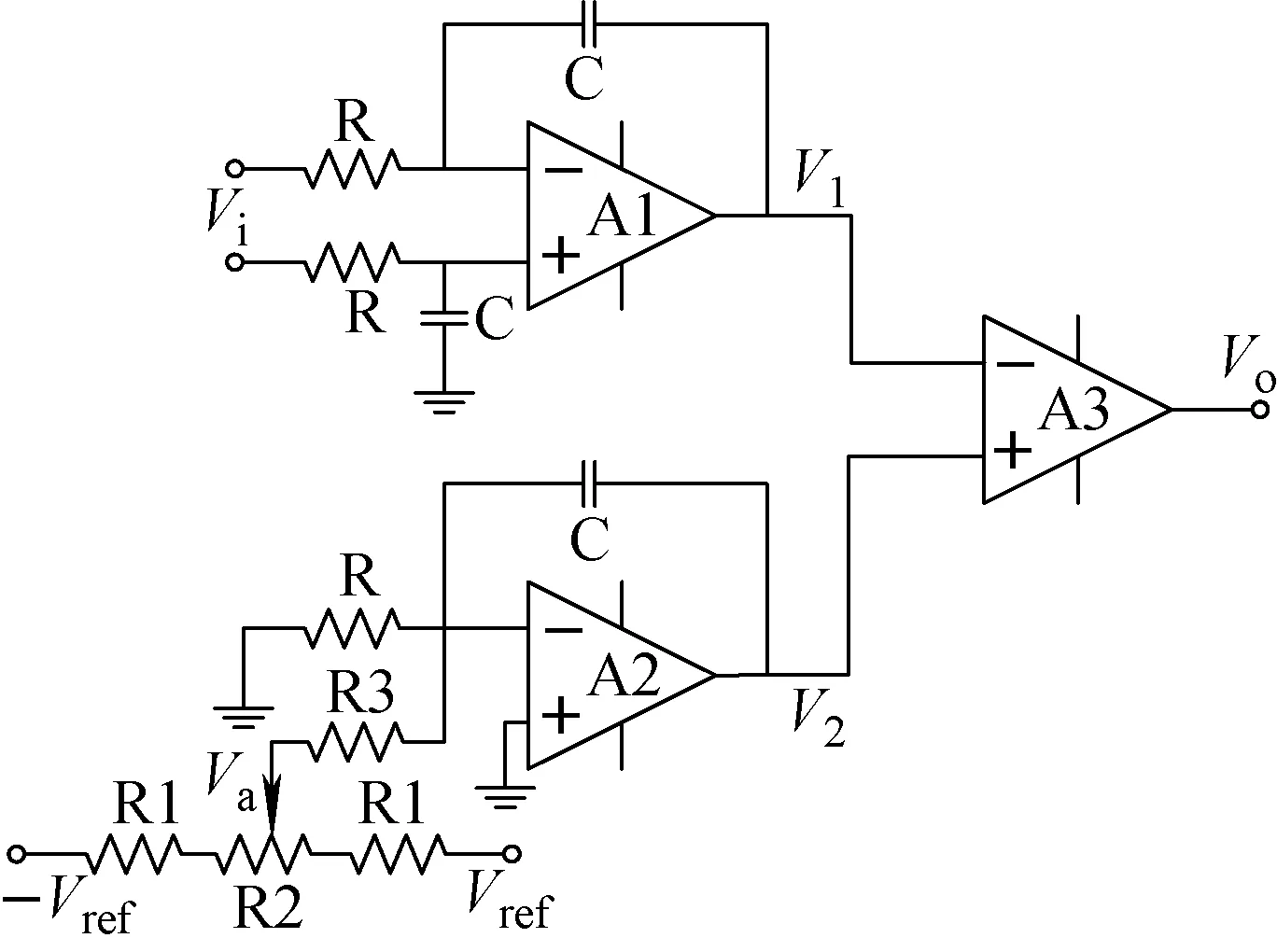
图3 差分积分器调零电路

差分积分器输出为：

(6)

其中，Vb1为运放A1的失调电压、失调电流以及外部干扰等引起的输入误差。

单端积分器输出为：

(7)

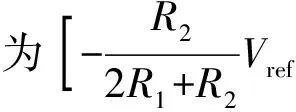
经过增益为1的仪表放大器A3后，Vo为：

(8)

则积分漂移由下式表示：

(9)

由于Vb1和Vb2在一定时间内是相对稳定的，因此可通过调节R2的阻值改变Va，使积分漂移接近于0，从而起到减小积分漂移的作用。

运算放大器A1和A2选择零漂移LTC1151运算放大器，其输入失调电压典型值为0.5 μV，失调电流典型值为±20 pA，失调电压漂移典型值为±0.01 μV/℃，相关参数较运算放大器OP07提高了1～2个数量级。仪表放大器A3选择高精度仪表放大器INA114，此外还采用具有低泄漏电流的聚苯乙烯电容和高精度、低温度系数的电阻，以尽可能减少器件带来的误差。

2 系统测试

对积分时间常数RC为20 ms的差分积分器进行了测试。将输入两端短路，测试其积分漂移，结果示于图4。由图4可见，通过调零电路调节其漂移后，100 s积分漂移约为0 V(图4a)，说明调零电路能有效调节积分漂移，且调节后积分漂移较稳定；当共模电压为0.13 V时，100 s积分漂移约为0 V(图4b)，说明0.13 V的共模电压对积分漂移基本无影响；当共模电压加大到1.5 V时，100 s积分漂移约为4 mV(图4c)，相当于80 μWb，说明1.5 V的共模电压对积分漂移有一定影响。

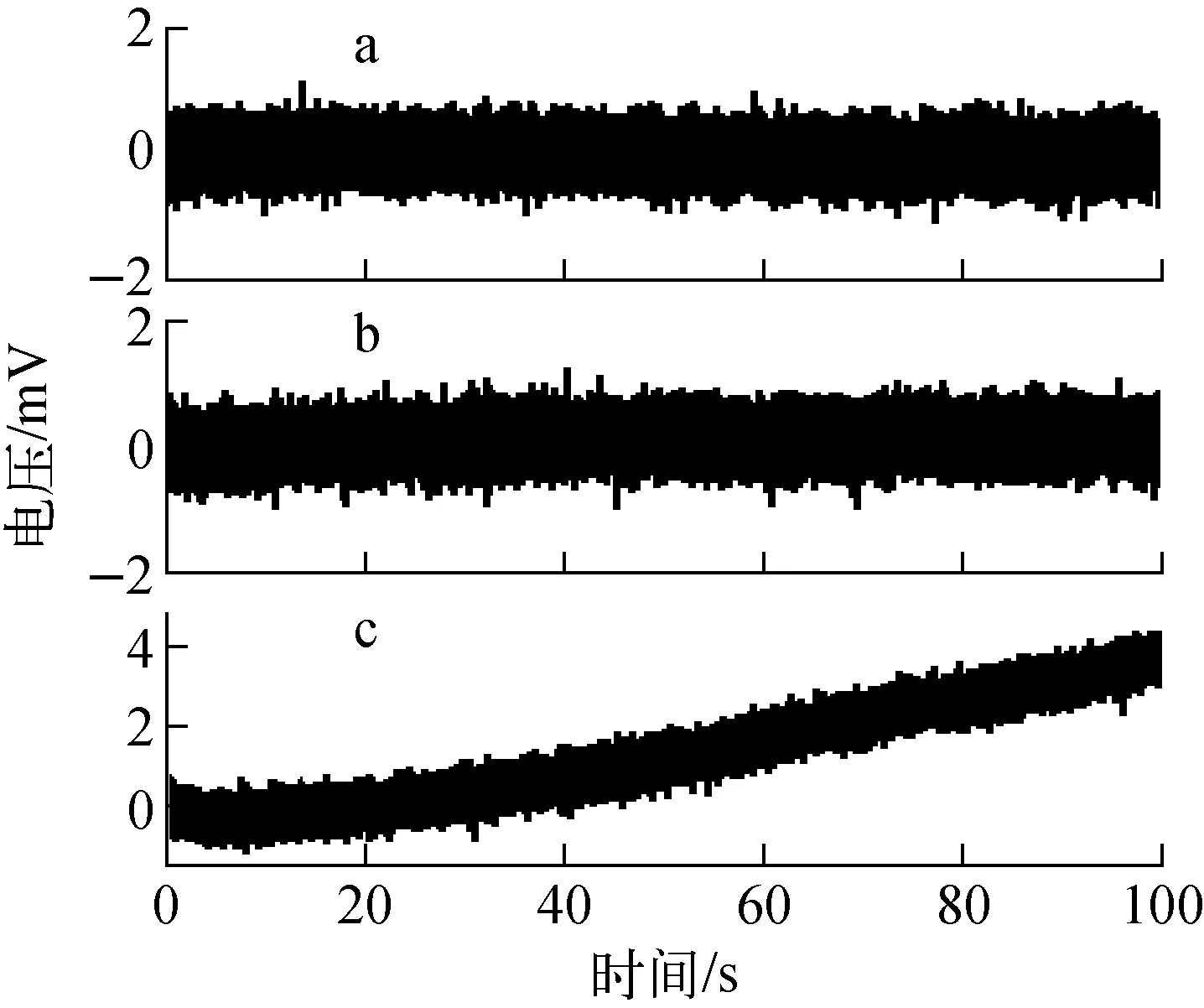
图4 共模电压分别为0 V(a)、0.13 V(b)和1.5 V(c)时20 ms差分积分器100 s积分漂移

套用差分放大器共模抑制比的概念，定义差分积分器的共模漂移抑制比为积分器对差模信号的积分漂移率Adf与对共模信号的积分漂移率Acf之比。即该差分积分器的共模抑制比CMRR为：

≈125 dB

共模抑制比越高越好。要提高差分积分器的共模抑制比，主要应提高差分积分器中前端两路积分器的一致性，即运放、积分电阻和积分电容的一致性。一般情况下，积分器输入端的共模电压在mV量级，其对差分积分器产生的影响可忽略。

3 应用

图5为单匝环相对测量法连接示意图。单匝环1作为参考，其他单匝环信号与其相减，再由积分器进行积分用于反演计算。这样连接的好处是可去除参考单匝环1产生的磁通值Φref，只需考虑相对变化量，如Φ2-Φref，Φ3-Φref等，这样即可用积分时间常数相对较小的积分器来实现，从而提高信号的信噪比。采用相对测量法时使用的是200 ms积分时间常数积分器，而采用绝对测量法时使用的是600 ms积分时间常数积分器。

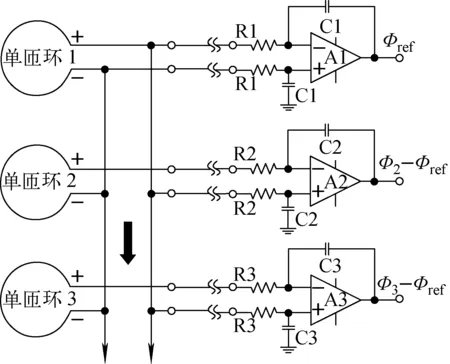
图5 单匝环相对测量法连接示意图

图6为采用图5方法连接后对极向场线圈进行预设波形通电测试得到的单匝环3的信号，其中，图6a为实际测量值，图6b为利用极向场线圈罗轲测量后的计算值。由图6可见，单匝环信号的计算值和测量值一致，说明差分积分器测量结果准确。

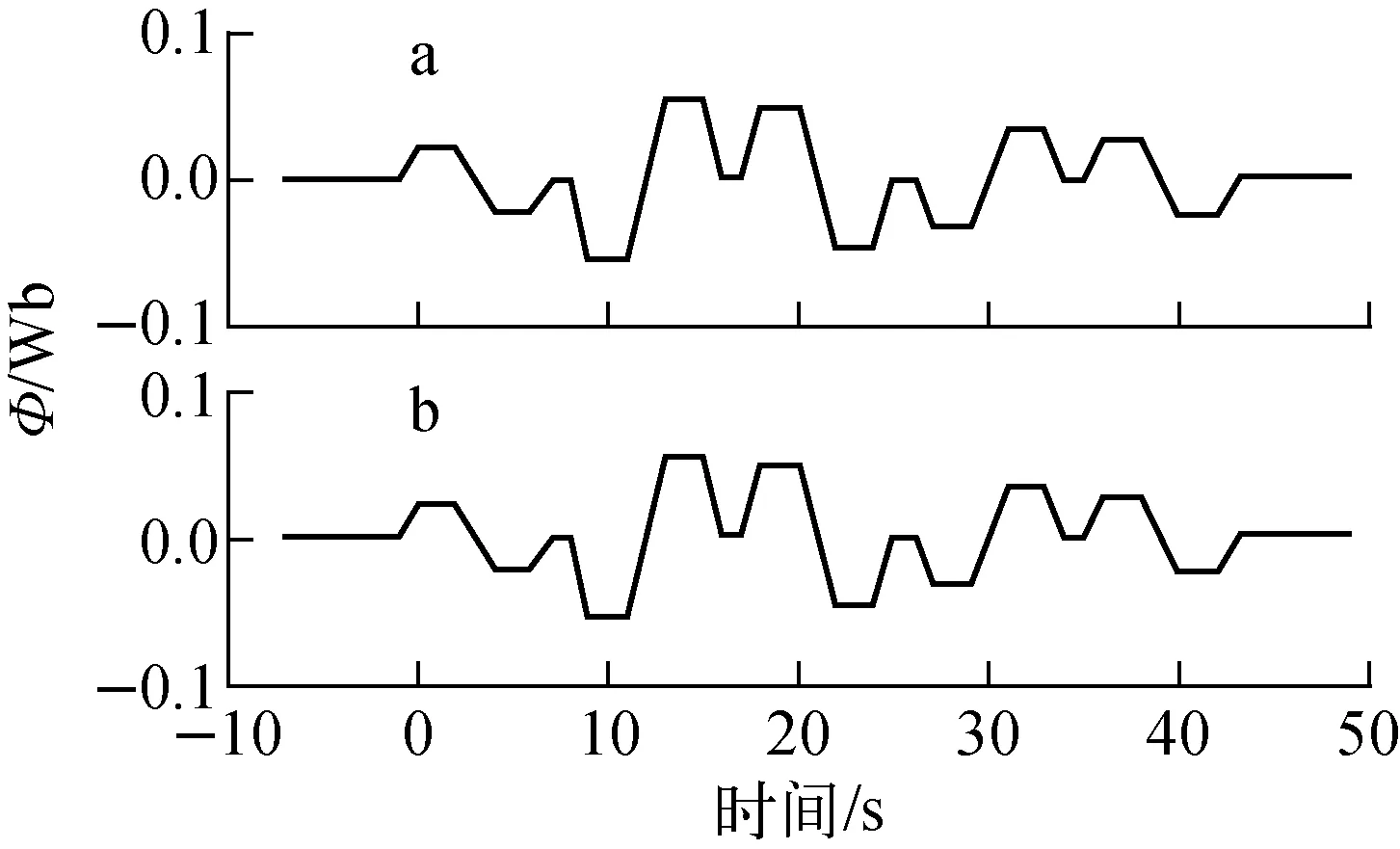
图6 单匝环3的测量值(a)与计算值(b)

如果单匝环相对测量法不采用差分积分器，而采用单端积分器，由于单端积分器的“+”端直接连接到信号地，并与单匝环1的公共端连接在一起，这样势必在连线上造成很多地环路，从而引入干扰。单匝环相对测量法采用200 ms单端积分器和差分积分器的测量结果示于图7。由图7可见，单匝环采用相对测量法时，以单匝环3为例，采用200 ms单端积分器测量，30 s漂移量达到2.2 mWb(图7a)，漂移较大且经常不稳定，难以调节。而采用200 ms差分积分器后积分漂移明显改善(图7b)，且较为稳定，易于调节。由此可见，在采用相对测量法时，差分积分器明显优于单端积分器。

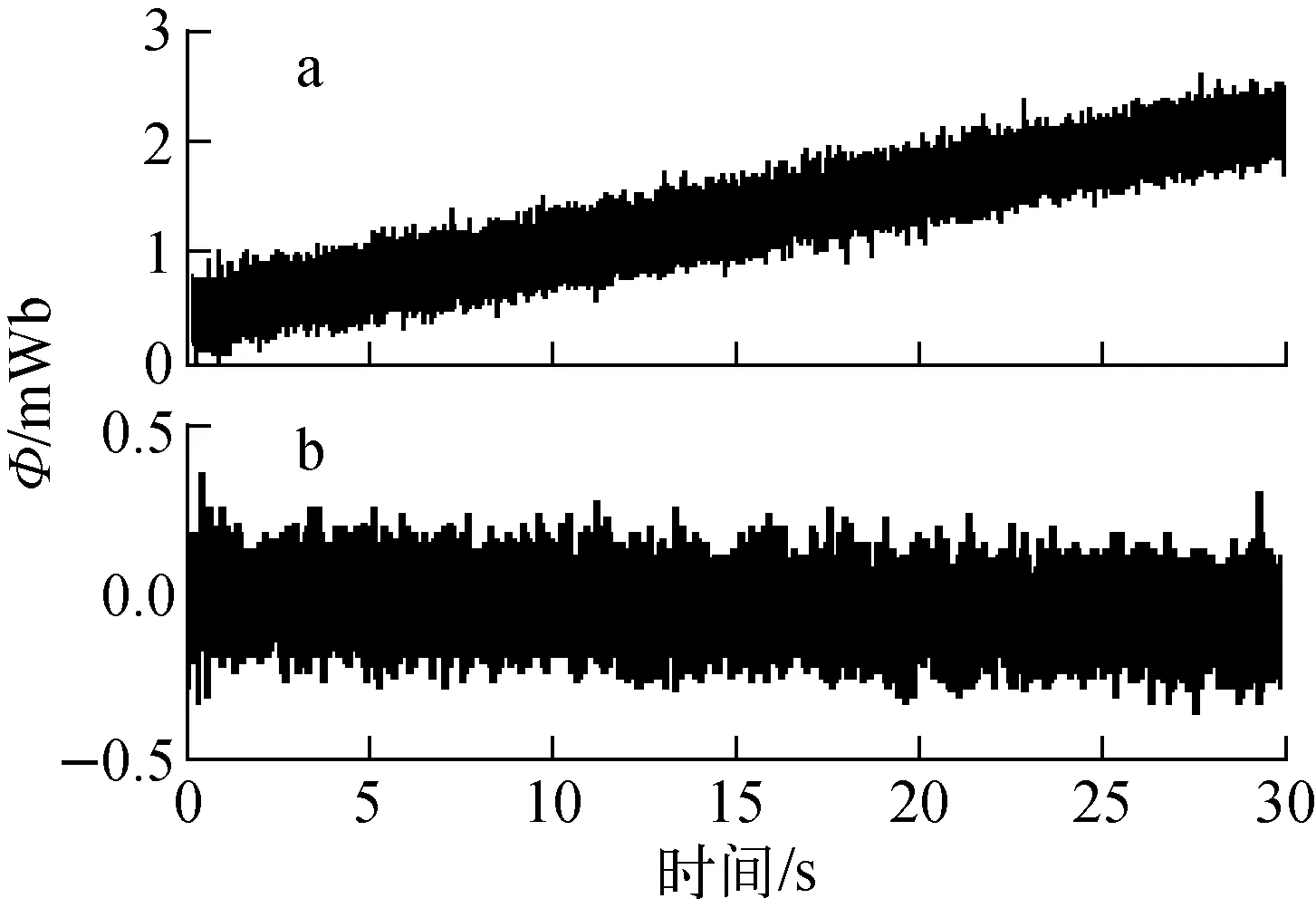
图7 单端积分器(a)与差分积分器(b)效果比较

4 结论

本工作研制的差分积分器实现了对差分输入信号积分及对共模输入信号抑制的功能，积分正确，积分漂移稳定且易于调节，在共模电压为1.5 V时，100 s积分漂移为80 μWb，共模抑制比高达125 dB。该差分积分器已成功应用于2012年的EAST实验中，效果明显优于单端积分器，表明其在今后托卡马克放电实验的电磁测量中有着较大的应用价值和前景。

参考文献：

[1] WAN Yuanxi, LI Jiangang, WENG Peide, et al. First engineering commissioning of EAST Tokamak[J]. Plasma Science and Technology, 2006, 8(3): 253-254.

[2] WU Songtao, EAST Team. An overview of the EAST project[J]. Fusion Engineering and Design, 2007, 82: 463-471.

[3] SHEN B, WANG B N, ZHANG X Q. Diamagnetic measurement on HT-7 superconducting Tokamak[J]. Fusion Engineering and Design, 2004, 70(4): 311-318.

[4] STRAIT E J. Magnetic diagnostic system of the DⅢ-D Tokamak[J]. Review of Scientific Instruments, 2006, 77(2): 023502.

[5] LIU D M, WAN B N, WANG Y, et al. A new low drift integrator system for the Experiment Advanced Superconductor Tokamak[J]. Review of Scientific Instruments, 2009, 80(5): 053506.

[6] 王勇，罗家融，季振山，等. 可变积分时间常数的长时间积分器[J]. 原子能科学技术，2010，44(3):368-371.

WANG Yong, LUO Jiarong, JI Zhenshan, et al. Long pulse integrator of variable integral time constant[J]. Atomic Energy Science and Technology, 2010, 44(3): 368-371(in Chinese).

[7] BAK J G, LEE S G, the KSTAR Project Team. Performance of the magnetic sensor and the integrator for the KSTAR magnetic diagnostics[J]. Review of Scientific Instruments, 2004, 75(10): 4 305-4 307.

[8] WERNER A. W7-X magnetic diagnostics: Performance of the digital integrator[J]. Review of Scientific Instruments, 2006, 77(10): 10E307.

[9] OTT H W. 电子系统中噪声的抑制与衰减技术[M]. 2版. 王培清，李迪，译. 北京：电子工业出版社，2003:65-66.

[10] 童诗白,华成英. 模拟电子技术基础[M]. 2版. 北京:高等教育出版社，2002:146-152.