一种混合式系留无人机高度伺服系统控制方法研究*

殷严刚

(桂林飞宇科技股份有限公司，广西 桂林，541004)

1 引言

多旋翼无人机具有结构简单、灵活机动等特性，用途非常广泛[1-3]，因此引起了研究者们的研究兴趣[4-6]。传统的无人机无法长时间驻留空中执行任务，将无人机和地面供电系统通过一条供电缆绳连接起来，可以实现无人机长时间驻留空中作业，可应用于室内定位[7]、视觉伺服[8]和公安监控等。收放缆伺服系统是整个系留无人机系统的关键环节，在无人机的飞行高度和升降控制中起决定性作用[9]，它通过伺服电机驱动传动机构带动绕线盘转动，对线缆进行绕线和排线，调整收放线的速度和长度。

所有控制系统在实际控制环境下都会受到来自内部或者外部的干扰，如何抑制扰动是控制的一个重要问题。系留无人机收放缆伺服系统除了受到摩擦力作用外，在空中悬停时，还易受到气流的干扰，从而引起位置变化和高度变化。同时，无人机自身姿态调整时，会使紧绷状态的系留缆绳的张力发生变化，并通过绕线盘和传动机构在电机转轴上形成变化的干扰力矩，此时的被控对象具有非线性特性和时变特性。文献[9]建立了系绳模型，基于该模型的基础上开发了飞行控制系统结构和自动着陆状态机，文献[10]建立了系统的全局动力学模型，并提出了一种在倾斜（非平坦）地面上着陆的控制方案。文献[11]将收放缆伺服系统视为恒张力控制系统并采用经典PID控制方法，但未考虑到经典PID控制应对非线性系统的局限性。文献[12]提出了基于二阶非线性跟踪-微分器自适应神经网络控制方法，对非线性系统具有较好的控制效果，但未能解决指令信号的二阶微分提取问题。本文提出采用有限时间收敛三阶跟踪-微分器来解决二阶微分提取问题，在借鉴自抗扰控制的主动抗扰原理的基础上，将系统不确定项视为总扰动并使用RBF神经网络对其进行逼近，使用基于前馈加扰动补偿的PD控制律应用于系留无人机收放缆高度伺服系统控制，提高系统控制精度和抗干扰能力。

2 系统描述

本系留无人机系统采用直流电机，忽略电枢电感,建立伺服系统的动力学方程为[11,13]：

其中，u(t)为控制输入，Ce为反电势系数，R为电枢电阻，Km为电机力矩系数，Ku为PWM功率放大器放大倍数，J为等效到电机转轴上的转动惯量，θ为电机转角，Tf(t)为干扰力矩，Ff(t)为黏性摩擦模型：

式(2)中，Fc为库仑摩擦力，sgn(∙)是符号函数，kv为黏性摩擦力矩比例系数。令θ=x，将式(1)中不确定项视为未知的非线性函数f(x)，即总扰动，视为建模确知部分并令其为f(x)，则式(1)可表示为如下二阶非线性系统：

设理想跟踪指令为θd，则误差为：e=θ d-θ=θd-x，E=[]T。

设计基于前馈加扰动补偿理想的PD 控制率[13]为：

将式(4)式代入(3)式中，得到误差方程为：

设计K=[k pkd]T，使(5)式的多项式s2+k ds+kp=0特征根都在复数域的左半平面，使得当t→∞时，e→ 0且→0，系统的输出会逐渐收敛于理想值。

3 自适应RBF 神经网络

若式(3)未知的非线性函数f(x) 未知，则控制率式(4)无法实现。RBF 神经网络对非线性连续函数具有较好的局部逼近效果[14]，可利用RBF 神经网络对f(x) 进行逼近，由此来解决式(4)扰动的补偿问题。RBF 神经网络是前向三层网络结构，隐含层数越多逼近效果越好，但计算量也会随之增加。取X=[]T作为网络的输入，经过实验反复调试，在能满足逼近效果的最低要求的提前下，取最终采用2-5-1 双输入单输出的RBF网络。设RBF 神经网络的高斯基函数的宽度向量为：，径向基向量为：H=[h1,h2,…,hj,…,hm]T，其中hj为隐含层第j个神经元的输出，即如公式(6)所示：

公式(6)中，bj为隐含层节点j的基宽参数且bj＞ 0，Cj为隐含层的的第j个节点的中心向量，，网络输出层的权向量为：

网络输出不确定项的估计值为：

为确保整个闭环系统的稳定性，基于Lyapunov 稳定性理论分析设计RBF 神经网络权重调节的自适应率为[13]：

式(9)中，γ是可调参数，，Q 为任意的2 ×2 正定矩阵，P 是满足如下Lyapunov 方程的对称正定矩阵：

4 有限时间收敛三阶跟踪-微分器

由式(4)可知，控制率中含有输入信号的二阶微分项，而采用差分法求解的方式误差太大。为了解决这个问题[15-16]，本文在此提出采用有限时间收敛三阶跟踪-微分器来实现理想跟踪指令信号θd跟踪、提取指令信号θd的一阶导数和二阶导数，其表达式如下：

上式中v(t)为待微分的输入信号，x1为输入信号的跟踪信号x1=θd,x2为输入信号一阶微分的估计x2=，x3=为输入信号二阶微分的估计，ε决定跟踪的快慢，仿真研究过程中发现ε过大时跟踪速度下降，ε过小则会造成输出信号品质变差，故需适当选取，本例中的经验取值范围：0.03～0.1。

5 仿真分析

为研究本文控制方法的性能特点，依次采用常规PD 控制和基于三阶跟踪-微分器与自适应RBF 神经网络补偿(RBFPD)控制，对系留无人机收放线缆伺服系统的电机转角动力学方程分别进行控制仿真分析。参考文献[11-13]，选取伺服系统参数为：Ce=0.6V/(rad/s)，R=3.8Ω，Km=3N ∙m/A，Ku=11V/V，Fc=10N ∙ m，kv=1Nms/rad，J=0.3kg ∙m2；Tf(t)的幅值范围：0～50N ∙ m，选取RBFPD 控制器参数：K=[5 200]T，ε=0.03，选取常规PD 控制器参数：kp=200,kd=5。

给定指令信号为单位阶跃信号下，由图1 单位阶跃响应局部放大图可见RBFPD控制的上升时间为0.057s，超调量为3.5%，PD控制下的上升时间为0.125s，无超调，在满足超调量要求的前提下，在系统响应速度上，RBFPD控制在PD控制基础上提高了1.19倍。由图2 误差曲线的局部放大图可知，RBFPD控制的最大稳态误差为0.005rad，PD控制的最大稳态误差为0.020rad，RBFPD控制的稳态误差在PD控制的基础上减小了0.75倍。

图1 单位阶跃响应测试

图2 单位阶跃响应误差曲线

图3 正弦信号位置跟踪

图4 正弦信号位置跟踪误差曲线

由图5 和图6 可见，采用标准的有限时间收敛三阶跟踪-微分器来实现指令信号θd跟踪，稳定的最大误差为0.006 rad，提取指令信号的一阶微分与理想值稳定的最大误差为0.036 rad，但其输出的二阶导数x3存在毛刺现象，初始微分值过大达62.80rad，稳定的最大误差为2.80rad。本文通过在其二阶导数输出端增加小时间常数的一阶惯性环节，其中T=0.05。通过滤除噪声后得到二阶微分信号x4，初始峰值为10.76rad，在原基础上减小了4.84 倍；稳定的最大误差为1.45rad，在原基础上减小了0.48 倍。由图6 局部放大图可见滤除噪声后有效改善了跟踪-微分器的二阶微分输出波形。

图5 指令信号跟踪和提取一阶微分

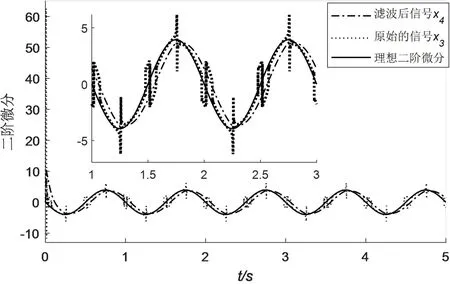
图6 改善的二阶微分输出波形

6 结语

本文针对系留无人机收放缆高度伺服系统非线性和时变特性，在借鉴自抗扰控制的主动抗扰原理的基础上，提出一种基于三阶跟踪-微分器与自适应RBF 神经网络补偿控制方法。通过仿真实验对比发现，具有扰动估计补偿能力的控制方法比传统PD 控制有更高的控制精度、更强的抗干扰能力，对提高系留无人机收放缆高度伺服控制系统的性能具有较好的应用价值。