利用试探波函数估计简谐振子基态能级*

伊 雯，邱环环，汪剑津

(江西科技师范大学物理系，江西 南昌 330013)

1 引言

量子力学作为物理系本科生的一门必修课程，由于涉及很多的数学以及与经典物理观念产生强烈的冲突常常被学生冠以难懂难学的名号。针对这种情况，学生唯有多做习题、勤加练习才能攻坚克难学好量子力学。正如樱井在他经典的《现代量子力学》序言中所说的那样：如果一个人学完全书但不会做练习那么他什么也没学到[1]。由此可见，习题的训练对学习量子力学的重要性。而实际上不仅仅对于量子力学，对于其他任何一门理工科课程都是如此。

通常来讲，量子力学主流的表述方法有三种，即波动力学，矩阵力学以及路径积分，它们的代表人物分别是薛定谔，海森堡，费曼。波动力学的核心是薛定谔方程，它的地位犹如经典力学中的拉格朗日方程或者哈密顿正则方程，规定了微观粒子如何运动。矩阵力学的核心是希尔伯特空间，希尔伯特空间即由系统正交归一化的能量本征态所支起来的空间，波函数可以理解为希尔伯特空间的一个向量。路径积分的核心是由作用量所定义的传播子和费曼图，路径积分在高能物理和量子场论中具有极其深远的影响。由于路径积分所要求的基础理论物理知识和数学知识要高于波动力学和矩阵力学，所以通常的本科学习阶段接触的主要是波动力学和矩阵力学。

如果说波动力学的核心是薛定谔方程，那如何求解形如下式的定态薛定谔方程是波动力学的核心任务：

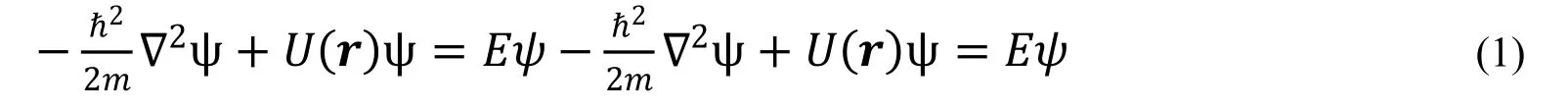
定态薛定谔方程的求解通常是困难的。能严格求解的也就几个模型，如常数势，简谐振子，二体中心力场模型。对于稍微复杂一点的情况如氦原子或者氢分子想要严格求解已是不可能。然而人的求知欲是不可能停止的，于是就发展出了微扰论和变分法。微扰论和变分法都需要一个能严格求解的模型为基础才能继续往下走。微扰论可以同时给出能级的修正和波函数的修正，修正的级数越高所得结果就越接近真实情况，同时，代价是计算过程也更加的复杂和冗长，通常能级到二级修正波函数到一级修正即可。微扰论要求作为微扰的能量项要足够小才行，否则修正级数再高也是于事无补。变分法对此没有要求或者说变分法中并没有微扰的概念，它只把哈密顿量分解为可解的部分和剩余的部分。对氦原子基态能级的估计是它的一个典型的应用。变分法的关键是构造出合适的试探波函数从而才能达到对系统基态能级的准确估计。而本文所要做的就是研究试探波函数对估计系统基态能级的影响，为试探波函数的构造提供一些建议。

在正式进入我们的研究之前，这里有必要先介绍一下变分法的原理，同时考虑到变分法在任何一本量子力学教材上都可以找到相应的内容，因此我们只做一简短的介绍。设ψ是任意一个归一化的波函数，它在系统能量本征态上的展开可以写为：

其中Ψn为对应能量为En的正交归一本征态，即有。这里我们约定Ψ0和E0为系统的基态波函数和基态能级。根据量子力学中力学量的期望值的定义我们有Ψ状态下的能量的期望值为：

其中积分遍及整个空间。把(2)代入(3)并利用Ψn的正交归一性可得能量的期望值为：

可以看到任意的波函数其能量的平均值总是会大于系统的基态能量。而变分法则体现在求出关于某个参数λ的极小值，即：

其中参数λ来源于试探波函数Ψ。根据以上的讨论可知变分法给出的是基态能级的上限。在利用变分法的时候有两点需要注意：一是试探波函数要先进行归一化处理；二是试探波函数需要包含两个参数，这是归一化和极值两个条件所限定的。

为了研究试探波函数对估算系统基态能级的影响，我们需要一个可以严格求解的模型作为基准来对照。而这一个模型很容易就可以想到的是简谐振子模型。不仅其能级具有简单的表达式，它的基态波函数也非常的简洁是一个高斯函数，非常适合本文的研究目的。通过研究，我们发现在使用变分法时除考虑到波函数的宇称性外若放弃波函数光滑性的严格要求反而能获得更好的估算结果，进一步发现，由于线性波函数的一次函数特性从根本上忽略了动能项对能量的贡献，因此无论如何也不能把作试探波函数选为线性函数的。我们的研究对于学生掌握变分法、试探波函数的选取、认识力学量需用算符表示的思想都将有所帮助，从而有助于他们量子力学的学习。

2 模型

首如前文所述，我们采用的是可解的简谐振子模型，针对我们所要研究的问题我们以一维的系统为例，其哈密顿量如下所示：

为了之后的讨论方便，我们首先对系统的哈密顿量做无量纲的处理，令m=ℏ=ω=1，于是得到无量纲的哈密顿量：

图1 用于估算基态能级的试探波函数

3 结果和讨论

3.1 试探波函数I

实由于简谐势没有奇异性，波函数需连续且光滑。为此我们首先考虑形如的波函数,该函数称为Lorentz函数，常用于功率谱的分析计算某一频率的波所受的散射强度的大小。它在全空间是连续且光滑的，其图形如图1中的“横-点点”线所示。接下来我们采用变分法来看一下它对基态能量的估计。

3.2 试探波函数II

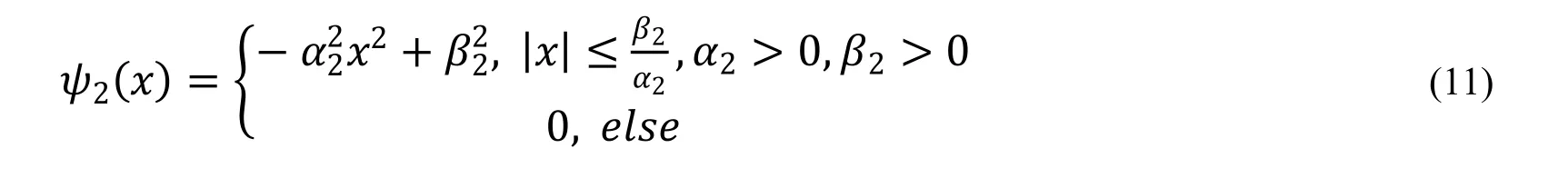
试探波函数II是分段波函数，由向下开口的抛物线和常数0构成。其形状我们用“横-点”线画在图1中。很明显的可以看到在x=2附近是不光滑的。同样的根据归一化条件，注意此时波函数是分段的需要改变一下积分限，，可以得到。再求能量的期望值：

3.3 试探波函数III:

试探波函数III也是分段波函数，由余弦函数和常数0构成。其形状我们用“横-横”线画在图1中。同样地可以看到在x=2附近也是不光滑的。根据归一化条件，同样注意积分限的变化，，可以得到。继续求能量的期望值：

利用α3和β3的关系得到，当且仅当时取等号。由此可知试探波函数给出的最好的结果是，它对真实能量的相对偏移度为。其估算结果相对于有了进一步的提高，粗略一点的话还是可以接受的。根据取最小值的条件可得到α3=0.754，β3=0.692。于是得到波函数为：

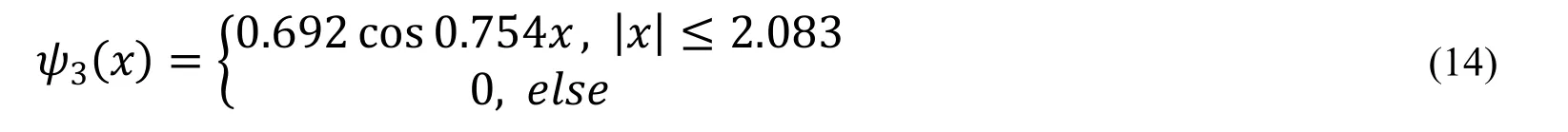
3.4 试探波函数IV

由于线性函数的一次特性，上式又可以写为：

可见线性函数直接忽略了动能项对能量的贡献。进一步求得能量的平均值为：

最后一步利用了k和b的关系。由最后结果可见线性波函数无法给出有意义的结果。证实了我们之前所说的线性波函数不能用作试探波函数的观点。

至此我们已经完成了4个试探波函数对基态能级的估计，我们把结果总结在了表1中。可以看到除不能作为试探波函数的线性函数外，两个不光滑的分段波函数给出的结果都比光滑的Lorentz试探波函数给出的结果要好，其中余弦给出的结果最接近真实基态能量。这也给我们一种启示是：在用变分法估算系统基态能级时，为了获得较好的估计结果，除考虑必要的对称性外是可以适当放宽波函数的光滑性要求的。

表1 试探波函数估算出的基态能量，相对于真实基态能量的偏离度γ，试探波函数与严格解高斯函数的相异度D。其中直线波函数给不出有意义的结果我们用横线表示

表1 试探波函数估算出的基态能量，相对于真实基态能量的偏离度γ，试探波函数与严格解高斯函数的相异度D。其中直线波函数给不出有意义的结果我们用横线表示

可以看见的是，试探波函数对基态能量估算的好坏和它们与严格解的契合度是直接相关的。从图1中可以看到Lorentz函数偏离严格解高斯函数是最大的，因此估算出的能量和真实能量相差也最大。对于余弦函数和抛物线函数不太好容易看出哪个偏离高斯函数多一点，于是我们定义一个物理量相异度D来刻画它们对高斯函数的偏离程度。D越大表示偏离程度越高，其定义如下：

考虑到波函数的对称性以及归一性D的定义又可以写为：

经过初步的理论计算我们发现该积分很难得到解析解，即使使用WolframAlpha也无济于事，于是我们寻求了数值计算。为了使用数值计算我们把积分进行了截断。把积分上限设定为100，积分步长设为10−4。经验证这一设定得到的精度已经足够高，继续增大积分上限或者减小积分步长带来的变化也是微乎其微的。数值计算结果显示在表1中的第4行。可以看到Lorentz函数，抛物线函数，余弦函数对高斯函数的相异度分别是0.176，0.153，0.107。这和预期是一致的。Lorentz函数偏离程度最大因此能量估算的结果最差，余弦函数偏离程度最低给出的结果也最好。

4 结论

我们以简谐振子模型为基础运用变分法研究了试探波函数对估算基态能量的影响。我们研究发现，在选取试探波函数的时除了要考虑必须的宇称性外是可以适当放宽波函数的光滑性要求的，否则限制太多未必能得到一个好的能量估算结果。进一步我们还发现，线性波函数是无论如何也不能用作试探波函数来估算基态能量的，这是因为它的一次函数特性本质上忽略了动能项对能量的贡献。因此选取试探波函数时可以完全把线性波函数排除在外。我们的研究对于学生掌握变分法、试探波函数的选取、量子力学中力学量需用算符表示的认识都将有所裨益，或许还可以提高他们对量子力学的学习兴趣从而激发他们量子力学的学习热情。