静质量波函数的周期性研究

罗广源

(广西大学机械工程学院，广西 南宁 530003)

1 引言

我们知道，狄拉克方程中的静质量项为零时，可将狄拉克方程拆成两个彼此独立的二分量方程，这是外尔方程的推导过程。宇称不守恒发现后，物理学家用二分量理论描述中微子，但后来中微子振荡实验证实了中微子质量不为零，中微子的波动方程应是四分量的狄拉克方程或马约拉纳方程，这似乎表明了宇称破坏应有更深层次的原因。我们知道，弱反应过程中W玻色子只和左旋的夸克和右旋的反夸克耦合，右手的W玻色子是不存在的。杨国琛等]1[曾提出W玻色子的一个理论，认为W玻色子是矢量象WV与轴矢象WA的线性组合

2 外尔方程的推导

设动能部分对应着自身的质量mk，频率νk，动量pk与波长λk，动能波群速度与粒子速度υ相同，根据德布罗意公式可以得到

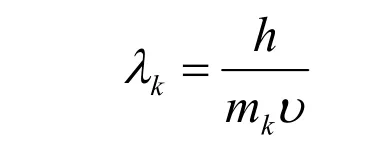
其中

由上可得动能波的形式为

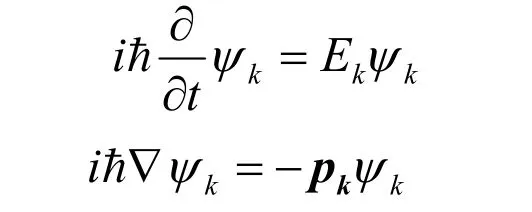
与传递电磁相互作用的光子，传递强相互作用的胶子及传递弱相互作用的Z玻色子不同，W玻色子的反粒子不是自身，而是相反电荷的W玻色子。中间玻色子动能写为

可以推导出玻色子的动能波动方程如下

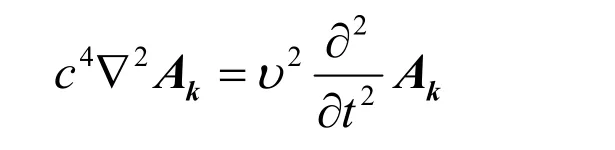
其中Ak为矢量。υ=c时，由上式即可得到我们熟悉的电磁波波动方程。

费米子的动能波动方程可以仿照狄拉克方程建立。由于电子波动方程是四分量的，其动能应写为

得到电子的动能波动方程

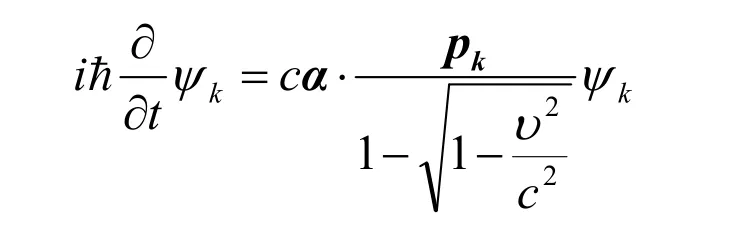
矩阵α与狄拉克方程矩阵相同，可以看到，费米子的自旋角动量与其动能部分有关，与静质量部分无关。该方程没有静质量项，即β-γ=0，有四个分量，没有破坏宇称，但由于没有静质量项，该方程本身具有拆成两个二分量方程的条件。在参与破坏宇称的弱相互作用时可以写成二分量形式

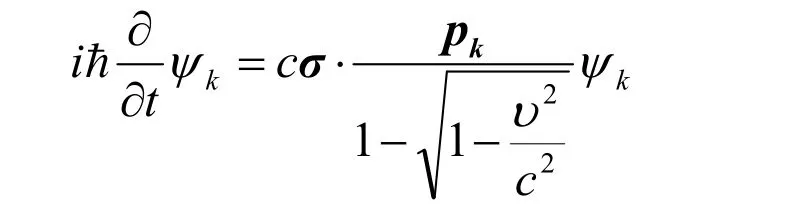
即当ψk与手性的W玻色子耦合时，只有上式二分量场参与相互作用（耦合为标量）。υ=c时，由该方程即可得到我们熟悉的外尔方程。

动能波函数ψk的平方是mk在空间中的分布函数，设粒子的静质量为m0对应的波函数为ψ0，ψk为粒子的旋量场，ψ为狄拉克方程中的旋量场，根据据质量守恒得到三者的关系式为

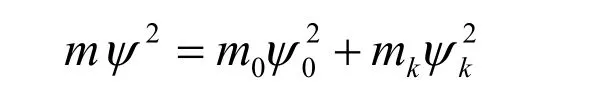
其中

3 静质量波函数的周期性探讨

ψ的频率为，ψk的频率为，设ν=νN0，，N,M均为正整数，为有理数，因此必为周期函数

ψ0可以看作频率为ν0整数倍的物质波叠加干涉，对于其中一个分波，，υ为粒子群速度，当ψ和ψ0的系数归一化时，通过傅里叶级数展开得到的各分波ψj的系数应自动满足归一化。

若电磁波的频率是ν0的整数倍，则量子场论中的相关积分计算只能代之以离散叠加，且电磁波波长只能取以下值

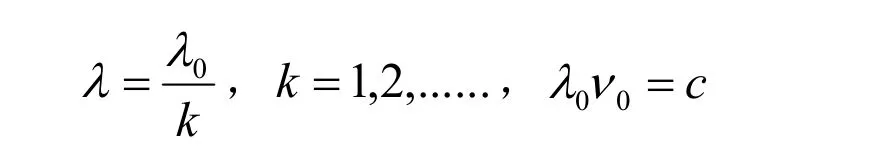
此前，我们没有关于研究物质波、电磁波频率是否连续的实验。建议在极低频(ELF)电磁波频段探测电磁波波长是否不连续，假设在波长λ1与λ2之间（λ1＞λ2）找不到任何电磁波，那么有

基本粒子的静质量下限

而希格斯场或其它潜在机制能否产生如此小的质量，决定自然界有无静质量为该数值的粒子。如果存在，根据标准模型，该质量可能对应中微子的一个质量本征态，且与中微子的质量顺序有关

最小静质量粒子相对应的速度只能取以下数值