关于主-从混沌蔡氏电路系统滞后同步的若干新判据*

卢雪菁，吴晓锋

（闽南师范大学数学与统计学院，福建漳州363000）

蔡氏电路系统是一类由三阶常微分方程描述并且可用简单的非线性电路实现的混沌系统[1-2]。多年来，它已成为研究混沌科学的一个基本模型。许多文献已证实，在特定的主-从反馈控制框架下，两个蔡氏电路系统可以实现混沌同步[3-33]。这些反馈控制框架包括线性状态误差反馈控制[3-20]、脉冲控制[21-23]、 采样控制[24-26]、 自适应控制[27-31]、基于观测器的控制和自适应滑膜控制等[32-33]。

本文研究线性状态误差反馈控制下的主-从蔡氏电路系统滞后混沌同步问题。所谓的线性状态误差反馈控制可描述为u（t）＝K（x-z），其中，x，z∈R3分别是主系统和从系统的状态变量，K∈R3×3为待定的常数控制增益矩阵。

文献[3]首先通过数值仿真证实了基于线性状态误差反馈控制的主-从蔡氏电路系统可以在控制增益矩阵K＝diag（k，0，0）、K＝diag（0，k，0）和K＝kI3等情况下达到混沌同步。文献[4]随后从理论上证明了控制增益矩阵K＝diag（k，0，0）情形下混沌同步的条件是反馈增益k＞6．4足够大，并且猜想控制增益矩阵K＝diag（0，k，0）情形也有类似的混沌同步条件。文献[5]进一步从理论上证明了这一猜想，但只得到了控制增益k在一个较小的区间内可保证混沌同步的保守结果。文献[6]改善了这一结果，证明了主-从蔡氏电路系统在控制增益矩阵K＝diag（0，k，0）情形下的混沌同步条件可以表示为k＞k*的形式。

许多研究者其后开始转向寻找所谓的代数型混沌同步判据，这种判据能够直观地用代数表达式给出由控制增益与蔡氏电路系统参数表示的混沌同步条件，因此很便于对控制器增益矩阵的设计。文献[7-17]证明了主-从蔡氏电路系统关于K＝（0，0，K3）∈ R3×3、K＝diag（k1，k2，k3）、K＝kI3和K＝diag（k，0，0）等控制增益矩阵情形下的代数型混沌同步判据，其中K3∈R3。

在主-从反馈控制框架中，主系统的状态变量信息传递到从系统端的控制器时客观存在有通道时延问题。文献[18-19]研究了主-从蔡氏电路系统在线性状态误差反馈控制下存在通道时延时的代数型滞后混沌同步判据，其中，控制增益矩阵为K＝diag（k1，k2，k3）和K＝diag（k，0，0）等情形。

上述对主-从蔡氏电路系统混沌同步的研究都是基于Lyapunov稳定性理论，因此，所获得的混沌同步判据都是充分条件。如何改进这些充分性混沌同步判据使它们更接近于混沌同步的必要条件，一直是混沌同步科学与技术领域的一个努力方向。本文基于文献[15-16]的频率域判据，采用多项式理论中的斯图姆定理和因式分解定理等工具，试图得到主-从蔡氏电路系统在线性状态误差反馈控制下达到滞后混沌同步的较少保守性的代数型判据，其中，混沌同步的滞后时间要求等同于主-从系统信息通道的时延时间，因此，这些新判据也适用于主-从系统通道时延为零的完全混沌同步问题。实例仿真表明，它们比现有的同类结果具有较少的保守性，即更接近于混沌同步的必要条件。

1 系统描述与同步框架

考虑如下无量纲形式的第一类蔡氏电路系统[1]：

和第二类蔡氏电路系统 ：

其中，a和b为正常数，r≥0，非线性项φ：R→R，且

m0和m1为满足m1＞m0的任意常数。

令x＝（x1，x2，x3）T∈R3，并引入属性参数α：当蔡氏电路属于第一类时，取α＝1；当蔡氏电路属于第二类时，取α＝0。那么，上述两类蔡氏电路系统可以表示为统一的矩阵形式：

其中，

并且，dα＝a（α＋m1），α∈｛0，1｝，非线性项σ：R→R满足

如果忽略蔡氏电路（1）或（2）中电感的电阻，那么r＝0。

把式（4）描述的系统作为主系统，如下的蔡氏电路系统作为从系统：

其中的A，B，C和非线性函数 σ：R→ R如式（5）或式（6）所示。在对从系统（7）施加一个控制u（t）后，可以得到一个由主-从蔡氏电路系统组成的同步框架：

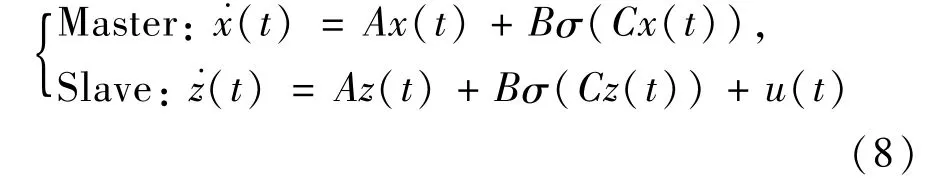
这里的u（t）选择为带有时延的线性状态误差反馈控制：

其中，K∈R3×3为待设计的常数控制增益矩阵，τ≥0是同步控制过程中主系统端的状态变量信号x（t）传输到从系统端的控制器时所可能存在的信号传输与处理时延，假设它为常值并且可能是未知的。显然线性状态误差反馈控制器（9）具有结构简单等优点。

我们的任务是设计控制增益矩阵K，使得对于主、从蔡氏电路系统的任意初始状态x（0）和z（0），下列极限被满足：

我们称满足条件（10）的主-从同步框架（8）达到滞后时间为τ的滞后同步。

令误差变量e（t）＝x（t-τ）-z（t）。由同步框架（8）可知该误差变量满足如下动力系统：

其中，非线性项η：R×R→R，并且

由于e（t）＝0时，η＝0，因此e（t）＝0是误差系统（11）的一个平衡点。显然，滞后同步问题（10）等价于误差系统（11）在平衡点e＝0的全局渐近稳定性问题。

定义1对于μ1＜μ2＜＋∞，称一维函数f（y）：R→R关于变量y∈R属于扇形[μ1，μ2]，如果对于任意的y∈R，

f∈F[μ1，μ2]＝｛φ∈ R：φ连续且

引理1由式（6）和式（12）确定的非线性项η关于变量Ce属于扇形[0，1]。

证明由式（6）描述的σ（y）可以表示为

显然，σ（y）关于变量y∈R是连续、非减的，并且对于任意y2＞y1∈R，（y1，σ（y1）和（y2，σ（y2））两点连线的斜率小于45°，即

（σ（y2）-σ（y1））/（y2-y1）≤1

因此，由式（12）描述的 η（Ce，Cz）关于变量Ce是连续的。

又当Ce＝0，即Cx（t-τ）＝Cz（t）时，η（Ce，Cz）＝0。

当Ce≠0，即Cx（t-τ）≠Cz（t）时，不妨先假设Cx（t-τ）＞Cz（t），那么必有

综上可知，η（Ce，Cz）关于变量Ce属于扇形[0，1]。

引理1表明，误差系统（11）是非线性项属于扇形[0，1]的Lur'e型系统。根据绝对稳定性理论[15]，如果Lur'e型的误差系统（11）在扇形[0，1]中是绝对稳定的，那么对于由式（6）和式（12）确定的η，对应的误差系统（11）在e＝0处就是全局渐近稳定的，这说明同步框架（8）达到（10）意义下的同步。因此，我们的任务转变为设计控制增益矩阵K，使得误差系统（11）在扇形[0，1]中达到绝对稳定。

2 主要结果

为了简化由（9）描述的控制器u（t）的结构，首先取控制增益矩阵K＝kI3。下面证明误差系统（11）在控制增益矩阵K＝kI3情况下达到绝对稳定的一个较少保守性的充分性判据。

首先，由文献[16]的定理1容易得到如下结果。

引理2令

其中，z为复变量，In为n×n维单位矩阵。令Rez为复数z的实部，λi（S）为实方阵S∈Rn×n的第i个特征值.如果Reλi（A-K）＜0，i＝1，2，…，n，并且

其中j2＝-1，那么误差系统（11）在扇形[0，1]中绝对稳定。

再令

定理1 误差系统（11）在控制增益矩阵K＝kI3情况下达到绝对稳定，即主一从同步框架（8）达到式（10）意义下滞后同步的条件是同时满足

并且，

①当蔡氏电路系统参数满足q＞0且l＞0时，同时满足

②当蔡氏电路系统参数满足q＞0且l＜0时，同时满足式（25）-（26）且

③当蔡氏电路系统参数满足q＜0且l＜0时，同时满足式（27）且

④当蔡氏电路系统参数满足q＜0且l＞0时，同时满足式（24）、式（28）-（29）。

证明 当控制增益矩阵K＝kI3时，令

注意到误差系统（11）属于扇形[0，1]，根据引理2，首先考虑矩阵A-K的特征值λ，它显然满足

根据矩阵理论中的 Hurwitz定理[34]，Reλ（AK）＜0当且仅当以下不等式同时成立：

由于系统参数a＞0，b＞0，r≥0，上述三个不等式同时成立的充要条件为式（19）-（21）同时成立。

又因为

其中Ω（·）由式（30）确定，因此，经过一些复数运算可以求得

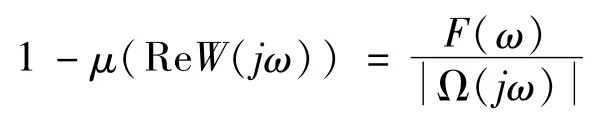
其中，表示复数的模，F（ω）＝ω6＋E1ω4＋F1ω2＋H1，E1，F1，H1分别由式（15）-（17）确定，误差系统（11）的扇形参数μ＝1。

由此可见，对于任意的μ（ReW（jω））＞0的充要条件F（ω）＞0。

令θ2＝ω。那么，不等式F（ω）＞0当且仅当

又因为多项式函数f（θ）＝θ3＋E1θ2＋F1θ＋H1关于θ∈[0，＋∞]是连续的，并有因此，不等式（31）成立的充要条件是f（0）＞0且f（θ）＝0在开区间（0，＋∞）上无实根。

由式（31）可知，f（0）＞0当且仅当H1＞0，或者在条件（21）下等价于不等式（22）成立。

又由多项式理论中的斯图姆定理可知[36]，f（θ）＝0在开区间（0，＋∞）上无实根等价于V（0）-V（＋∞）＝0，其中V（θ）表示关于f（θ）的斯图姆多项式序列在点θ∈[0，＋∞]上的符号变化次数[35-36]。

由f（θ）产生的斯图姆多项式序列为，其中，

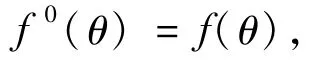
这里的E1，F1，H1，L1分别由式（15）-（18）确定。

由此可得到关于f（0）和f（＋∞）的斯图姆多项式序列如下：

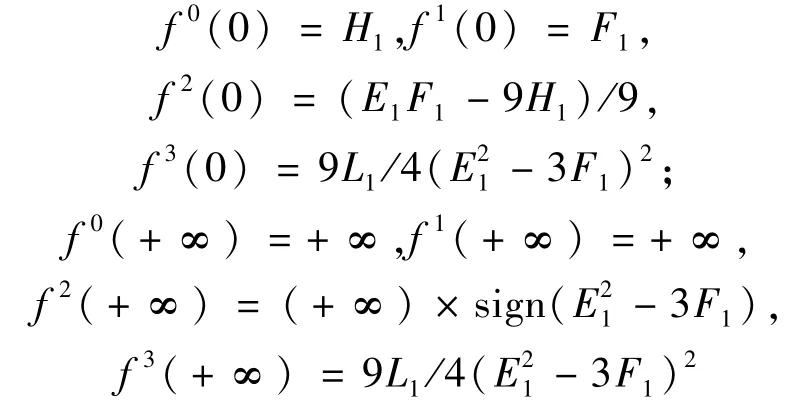
其中，sign（）表示符号函数。

由于要求H1＞0，关于f（0）的斯图姆多项式序列的符号序列为

关于f（＋∞）的斯图姆多项式序列的符号序列为

那么V（0）-V（＋∞）＝0成立当且仅当如下任一条件被满足：

条件1：V（0）＝V（＋∞）＝0，或等价于

条件2：V（0）＝V（＋∞）＝1，或等价于下列任一条件成立：

条件3：V（0）＝V（＋∞）＝2，或等价于下列任一条件成立：

由式（19）-（21）可知，上述同步条件中每个关于变量k的不等式都要得到形如k＞k*的解，才能保证与不等式（19）-（21）存在公共解。根据多项式因式分解定理[37]，这就要求每个不等式在变换成多项式不等式G（k）＞0的情形下，多项式G（k）关于变量k的最高次幂（有非零系数）的系数均要大于0。

由式（16）可知，多项式F1的最高次幂k4的系数为3，因此，我们应选择F1＞0的同步条件，这就排除了条件（34）、（37）、（40）-（41）作为同步条件的可能。

又由式（15）-（17）可知，多项式-3F1关于变量k具有非零系数的最高次幂为k2，其系数为q，多项式E1F1-9H1关于变量k具有非零系数的最高次幂为k4，其系数是2q，而由式（18）确定的多项式L1关于变量k具有非零系数的最高次幂为k6，其系数为16l。因此，

① 当q＞0，l＞0时，必须选择F1＞0，E21-3F1＞0，E1F1-9H1＞0，L1＞0作为同步条件，这时，只有条件（32）满足，这等同于不等式（23）-（26）同时成立。

② 当q＞0，l＜0时，应该选择F1＞0，E21-3F1＞0，E1F1-9H1＞0，L1＜0作为同步条件，这时，只有条件（33）满足，这等同于不等式（23）和（25）-（27）同时成立。

③当q＜0，l＜0时，应选择F1＞0，E21-3F1＜0，E1F1-9H1＜0，L1＜0作为同步条件，这时，只有条件（38）满足，这等同于不等式（23）和（27）-（29）同时成立。

④ 当q＜0，l＞0时，应该选择F1＞0，E21-3F1＜0，E1F1-9H1＜0，L1＞0作为同步条件，这时，只有条件（39）满足，这等同于不等式（23）-（24）、（28）-（29）同时成立。

综上所述，得证定理1。

下面进一步讨论一种更简单的控制增益矩阵K＝diag（k，0，0）的混沌同步判据。

令

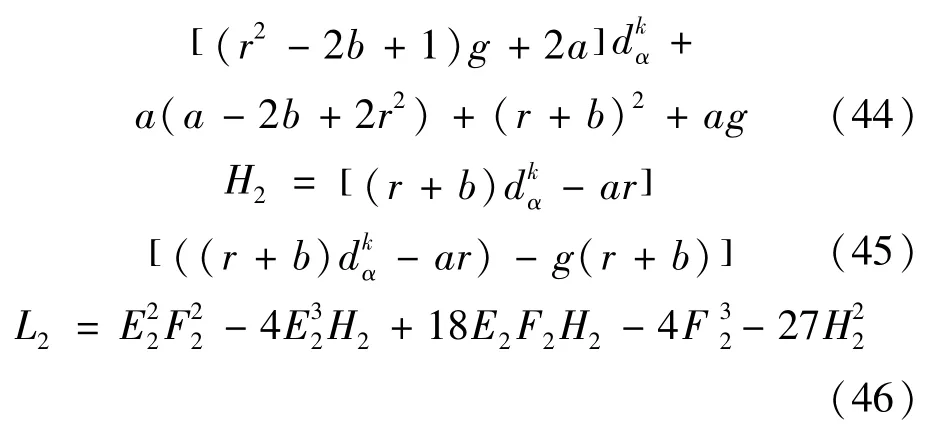
定理2误差系统（11）在控制增益矩阵K＝diag（k，0，0）情况下达到绝对稳定，即主一从同步框架（8）达到式（10）意义下滞后同步的条件是同时满足

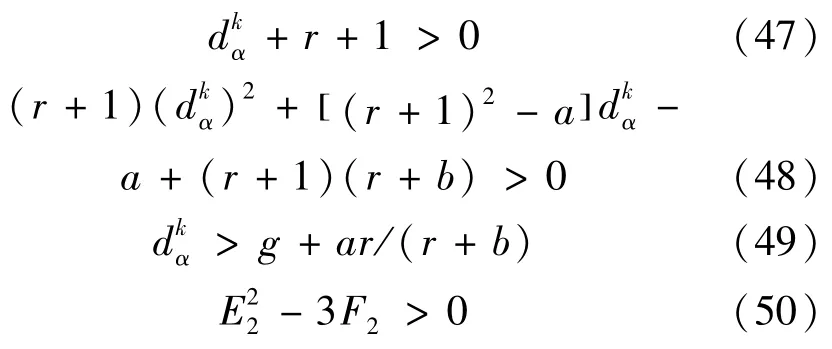
并且

①当蔡氏电路系统参数满足4b＜（r-1）2时，同时满足

②当蔡氏电路参数满足2（r2＋1）＞4b＞（r-1）2时，同时满足式（51）-（52）且

③当蔡氏电路参数满足4b＞2（r2＋1）时，同时满足式（54）且

证明在式（14）-（18）中令＋dα，h2＝1，h3＝r便可以得到对应于K＝diag（k，0，0）且由式（43）-（46）确定的E2，F2，H2和L2。

简单计算可以知道，多项式的最高次幂k4的系数为1，多项式F2的最高次幂k2和多项式E2F2-9H2的最高次幂k4的系数均为（r2＋1-2b），多项式L2的最高次幂k8的系数为（r2-1）2-4b（r＋1）2。那么，类似于定理1的证明方法可以得证本定理。

应该注意到同步目标（10）中的混沌同步滞后时间τ等同于主-从蔡氏电路系统的通道时延τ，而上述同步判据都与时延τ无关。这说明只要满足上述同步判据，主-从混沌蔡氏电路系统对于任意的通道时延τ都可以达到滞后同步，并且同步滞后时间自然地跟随主-从系统的通道时延。这个性质为工程应用带来了便利，同时也表明这些同步判据同样适用于如文献[3-17]所涉及的不考虑通道时延（即τ＝0）的主-从蔡氏电路系统完全混沌同步问题。

3 实例分析

关于主-从蔡氏电路系统在控制增益矩阵为K＝kI3和K＝diag（k，0，0）的线性状态误差反馈控制下的混沌同步判据已有一些结果[9，12，14，16-18]。本节将进一步地把本文得到的新的混沌同步判据与这些结果进行实例仿真比较。

文献[17]研究了主-从的第一类蔡氏电路系统在控制增益矩阵K＝kI3情况下的同步判据。令第一类蔡氏电路系统的参数值为：

再令主蔡氏电路系统的初始条件为x（0）＝（0.1，-0.2，-0.3）T，从蔡氏电路系统的初始条件为z（0）＝（-10，-5，-5）T。第一类主蔡氏电路系统的多螺旋混沌轨迹如图1所示。

图1 第一类主蔡氏电路系统的混沌轨迹Fig.1 The chaotic orbits of the first class of the master Chua's circuits

文献[17]证明了控制增益矩阵K＝kI3情况下的同步判据，由文献中的式（27）-（30）、（33）确定。根据该判据可以求得主-从蔡氏电路系统在上述参数值条件下的同步条件为：k＞6.4。文献[9]的定理4给出了另一个关于控制增益矩阵K＝kI3的同步判据，由此也可以求得主-从蔡氏电路系统在上述参数值条件下的同步条件：k＞40.41。

现在，我们考虑本文定理1中的判据。对于第一类蔡氏电路系统，dα＝a（1＋m1）。不难验证，在上述参数值情况下，q＝-56.75＜0，l＝-2.007×103＜0。因此，同步判据由式（19）-（23）、（27）-（29）确定。通过计算，可得到这些判据不等式的解依次为：k＞-1.4；k≥0.23；k≥-4.65；k≤-4.66或k≥3.85；任意实数k；任意实数k；k≤-6.2或k≥5.2；任意实数k。取这些解的交集可得关于控制增益矩阵K＝kI3的同步条件为：k≥5.2。显然，本文得到的同步条件优于文献[9]和[17]的结果。

图2 主—从蔡氏电路混沌系统在控制增益矩阵K＝5.5I3下的同步过程Fig.2 The synchronization evolution of the master-slave Chua's circuits by K＝5.5I3

取k＝5.5，它满足本文得到的同步条件，但不满足文献[9]和[17]得到的同步条件。图2显示了主—从蔡氏电路混沌系统在控制增益矩阵K＝5.5I3情形下的同步过程。

现在考虑控制增益矩阵K＝diag（k，0，0）的情况。

文献[16]研究了主-从的第二类蔡氏电路系统在控制增益矩阵K＝diag（k，0，0）情形下的同步问题，得到了文献中式（19）、（22）和（25）所示的3个同步判据。如果取第二类蔡氏电路系统的参数值为：

那么，由该3个判据得到的控制增益矩阵K＝diag（k，0，0）情形下的同步条件分别为：

现在采用本文定理2中的判据，此时dα＝am1。对于由式（58）给定的参数值，显然有2b＞r2＋1。因此，同步判据由式（47）-（50）、（54）-（56）确定。通过计算可以得到这些判据不等式的解依次为：k≥-3.571；k≥4.71或k≤-1.85；k≥-2.57；k≥1.29或k≤-2.58；k≤1.28或k≥9.166；k≤-2.47或k≥1.297；k≤-3.17或k＞1.23。取这些不等式解的交集，可以得到关于控制增益矩阵K＝diag（k，0，0）的同步条件为：k≥9.166。该条件显然优于上述文献[17]得到的3个结果。

令主蔡氏电路系统的初始条件为x（0）＝（0.1，-0.2，-0.3）T，从蔡氏电路系统的初始条件为z（0）＝（-10，-5，-5）T。取k＝10，它满足本文得到的同步条件，但不满足文献[16]得到的同步条件。图3和图4分别显示了第二类主蔡氏电路系统的混沌轨迹和主—从蔡氏电路系统在控制增益矩阵K＝diag（10，0，0）情形下的同步过程。

图3 第二类主蔡氏电路系统的混沌轨迹Fig.3 The chaotic orbits of the second class of Chua's circuits

文献[12，14，17-18]考虑了主-从的第一类蔡氏电路系统在控制增益矩阵K＝diag（k，0，0）情形下的同步问题。文献[12]得到的同步判据由其定理1描述；文献[14]得到的同步判据由其式（25）表达；文献[17]得到的同步判据由其式（36）确定；文献[18]得到的同步判据由其推论2描述。如果取蔡氏电路系统的参数值如式（57）所示，那么，文献[12，14，17-18]的同步判据所得到的控制增益矩阵K＝diag（k，0，0）情形下的同步条件分别为：k≥12.7λ（λ＞1）；k＞12.7；k≥18.40；k＞12.7。现在取本文定理2中的判据，此时dα＝a（1＋m1）。由于式（57）给定的参数值满足2b＞r2＋1。因此，同步判据由式（47）-（50）、（54）-（56）确定。通过计算可以得到这些判据不等式的解依次为：k＞-4.2；k≥5.3或k≤-2.61；k＞-3.2；k＞2.7或k＜-3.2；k≥11.77或k≤2.68；k≥2.73或k≤-3.13；k≥2.52或k≤-3.71。取这些不等式的交集，可以得到关于控制增益矩阵K＝diag（k，0，0）的同步条件为：k≥11.77。该条件显然优于文献[12，14，17-18]得到的上述结果。

图4 主—从蔡氏电路系统在控制增益矩阵 K＝diag（10，0，0）下的同步过程Fig.4 The synchronization evolution of the master-slave Chua's circuits by K＝diag（10，0，0）

图5 主—从蔡氏电路系统在控制增益矩阵K＝diag（12，0，0）情形下的同步过程Fig.5 The synchronization evolution of the master-slave Chua's circuits by K＝diag（12，0，0）

令主蔡氏电路系统的初始条件为x（0）＝（0.1，-0.2，-0.3）T，从蔡氏电路系统的初始条件为z（0）＝（-10，-5，-5）T。取k＝12，它满足本文得到的同步条件，但不满足文献[12，14，17-18]得到的同步条件。图5显示了主-从蔡氏电路系统在控制增益矩阵K＝diag（12，0，0）情形下的同步过程。

4 小 结

本文采用多项式理论中的斯图姆定理和因式分解定理，严格证明了主-从蔡氏电路系统在线性状态误差反馈控制下存在通道时延时的若干滞后混沌同步判据，其中涉及控制增益矩阵K＝diag（k，0，0）和K＝kI3等情形。实例分析表明，本文得到的同步判据比文献[12，14-15，17-19]的同类判据更少保守性。这一方法也可用于寻找其它控制增益矩阵或其它主-从混沌系统的同步判据。

[1]CHUA L O.Global unfolding of Chua's circuit[J].IEICE T Fund Electronics Commun Comput Sci，1993，76（5）：704-734.

[2]CHUA L O.Chua's circuit 10 years later[J].Int J Circuit Theory Appl，1994，22（4）：279-305.

[3]KAPITANIAK T，SEKIETA M.Monotone synchronization of chaos[J].Int J Bifurc Chaos，1996，6（1）：211-217.

[4]WU C W，CHUA L O.A unified framework for synchronization and control of dynamical systems[J].Int J Bifurc Chaos，1994，4（4）：979-987.

[5]WANG，X F，WANGZQ，CHEN G.A new criterion for synchronization of coupled chaotic oscillators with application to Chua's circuits[J].Int J Bifurc Chaos，1999，9（6）：1169-1174.

[6]ZHENG Y，LIU Z，ZHOU J.A new synchronization principle and application to Chua's circuits[J].Int JBifurc Chaos，2002，12（4）：815-818.

[7]WANG X F，WANG Z Q.Synchronization of Chua's oscillators with the third state as the driving signal[J].Int J Bifurc Chaos，1998，8（7）：1599-1603.

[8]LIU F，REN Y，SHAN X M，et al.A linear feedback synchronization theorem for a class of chaotic systems[J].Chaos Solitons Fractals，2002，13（4）：723-730.

[9]LIAO X X，CHAO G R.Some new results on chaos synchronization[J].Control Theory Appl，2003，20（2）：253-257.

[10]JIANG G P，ZHENG W X，CHEN G R.Global chaos synchronization with channel time-delay[J].Chaos Solitons Fractals，2004，20：267-275.

[11]WU X F，ZHAOY.Frequency domain criterion for chaos synchronization of Lur'e systems via linear state error feedback control[J].Int J Bifurc Chaos，2005，15（4）：1145-1154.

[12]LIAOX X，CHEN GR，XUB J，et al.On global exponential synchronization of Chua circuits[J].Int J Bifurc Chaos，2005，15（7）：2227-2234.

[13]JIANG G P，TANG W K S，CHEN G.A simple global synchronization criterion for coupled chaotic systems[J].Chaos Solitons Fractals，2003，15（5）：925-935.

[14]JIANG G P，TANG W K S.A global synchronization criterion for coupled chaotic systems via unidirectional linear error feedback approach[J].Int JBifurc Chaos，2002，12（10）：2239-2253.

[15]CURRAN P F，CHUA L O.Absolute stability theory and the synchronization problem[J].Int J Bifurc Chaos，1997，7（6）：1375-1382.

[16]WU X F，ZHAOY.Frequency domain criterion for chaos synchronization of Lur'e systems via linear state error feedback control[J].Int J Bifurc Chaos，2005，15（04）：1445-1454.

[17]WU X F，CAI JP，ZHAOY.Some new algebraic criteria for chaos synchronization of Chua's circuits by linear state error feedback control[J].Int J Circuit Theory Appl，2006，34（3）：265-280.

[18]JIANG G P，ZHENG W X，CHEN G.Global chaos synchronization with channel time-delay[J].Chaos Solitons Fractals，2004，20（2）：267-275.

[19]SUN J.Global synchronization criteria with channel time-delay for chaotic time-delay system[J].Chaos Solitons Fractals，2004，21（4）：967-975.

[20]王建根.非恒同主从耦合混沌系统一致同步的判据[J].中山大学学报（自然科学版），2005，44（2）：19-22.WANG J G.Uniformly synchronization criterion for non-identical coupled master-slave chaotic system[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2005，44（2）：19-22.

[21]SUN J T，ZHANG Y P.Impulsive control and synchronization of Chua's oscillators[J].Math Comput Simul，2004，66（6）：499-508.

[22]LI Z G，WEN C Y，SOH Y C，et al.The stabilization and synchronization of Chua's oscillators via impulsive control[J].IEEE T CAS-I，2001，48（11）：1351-1355.

[23]WANG Y W，WEN C，XIAO J W，et al.Impulsive synchronization of Chua's oscillators via a single variable[J].Chaos Solitons Fractals，2006，29（1）：198-201.

[24]ZHANG C K，JIANG L，HE Y，et al.Asymptotical synchronization for chaotic Lur'e systems using sampleddata control[J].Commun Nonlinear Sci Numer Simul，2013，18（10）：2743-2751.

[25]WANG Y Y，SHI P.On master-slave synchronization of Chaotic Lur'e systems using sampled-data control[J].IEEE T CAS-II，2016（99）：1.

[26]LEE T H，PARK J H.Improved criteria for sampleddata synchronization of chaotic Lur'e systems using two new approaches[J].Nonlinear Analysis：Hybrid Systems，2017，24：132-145.

[27]LIAO T L，LIN SH.Adaptive control and synchronization of Chua's circuits[J].Asian J Control，1999，1（2）：75-87.

[28]YASSEN M T.Adaptive control and synchronization of a modified Chua's circuit system[J].Appl Math Comput，2003，135（1）：113-128.

[29]YAOYAOL A N.Adaptive control for synchronization of Chua's circuit[J].J Comput Inform Systems，2013，9（14）：5751-5759.

[30]SALARIEH H，ALASTY A.Adaptive chaos synchronization in Chua's systems with noisy parameters[J].Math Comput Simul，2008，79（3）：233-241.

[31]SIDERSKIY V，KAPILA V.Parameter matching using adaptive synchronization of two Chua's oscillators[J].Int J Bifurc Chaos，2014，24（11）：212-3470.

[32]解玲丽，周毅.基于同步方法的观测器设计[J].中山大学学报（自然科学版），2008，47（5）：5-10.XIE L L，ZHOU Y.Observer design based on some synchronization technique[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2008，47（5）：5-10.

[33]YAN J J，LIN J S，LIAO T L.Synchronization of a modified Chua's circuit system via adaptive sliding mode control[J].Chaos Solitons Fractals，2008，36（1）：45-52.

[34]廖晓昕.稳定性的理论、方法和应用[M].武汉：华中科技大学出版社，2010.

[35]李师正.多项式代数[M].济南：山东教育出版社，1983.

[36]JACOBSON N.Basic algebra I[M].San Francisco：W H Freeman and Company，1974.

[37]王住登.高等代数[M].北京：国防工业出版社，2009.