基于PSO-LSSVM的矿井冲击地压分级预测研究

吕鹏飞，邱 林

(内蒙古科技大学 矿业研究院，内蒙古 包头 014010)

冲击地压是自然地质因素与工程扰动因素耦合作用下的一种非线性煤岩动力响应[1]。近年来，随着煤炭开采强度与深度增加，以冲击地压为代表的矿井动力灾害发生的频率和强度越来越大，因此在工作面开采之前实施必要的预测和防治措施对保障煤矿安全生产意义重大。以往的冲击地压预测主要以单因素预测方法为主，但日趋复杂的煤矿作业环境使单一指标预测法难以满足冲击地压预测的准确性要求，数值模拟和相似材料模拟也不能完全真实反映现场情况。因此，一些学者提出冲击地压预测的多因素耦合智能算法，例如：陈刚等[2]构建了基于神经网络与退火算法的冲击地压预测模型，这是国内较早的冲击地压智能预测模型；朱志洁等[3]针对ELM冲击地压预测模型中的权值误差和隐含层偏差问题，将GA算法引入ELM模型中，提出了具有较高预测精度的GA-ELM预测方法；尹光志等[4]利用混沌算法优化了神经网络模型，构建了冲击地压预测的CO-BP新模型；兰天伟等[5]提出了矿井冲击地压模式辨识概率预测方法，准确性较高。

以上冲击地压预测方法虽有一定优势，但可归纳出两点不足：一是预测指标体系不完善，专家学者在预测中往往选择对冲击地压影响较大的少数指标；二是多数算法要想获得更高的预测精度，就需要较长的训练时间，预测效率低。基于以上研究成果，综合考虑冲击地压发生的10个典型影响因素，提出基于PSO优化LSSVM模型的冲击地压预测方法，该方法预测中只需优化LSSVM模型中的核参数σ和惩罚因子f，具有计算效率高、预测精度高、操作简便等优点。

1 构建冲击地压分级预测指标体系

冲击地压危险等级划分和分级管理对煤矿安全生产至关重要。按照微震等级将冲击地压危险等级划分为5级：Ⅰ级为震级大于3.0级的冲击地压，属于特别重大灾害；Ⅱ级为震级2.0～3.0级的冲击地压，属于重大灾害；Ⅲ级为震级1.4～2.0级的冲击地压，属于较大灾害；Ⅳ级为震级0.6～1.4级的冲击地压，属于一般灾害；Ⅴ级为震级小于0.6级的冲击地压。不同等级的冲击地压灾害是不同量级的冲击地压影响因素耦合作用的结果，故综合考虑冲击地压影响因素是准确预测其危险程度的必要前提。预测指标如下：

1)开采深度：煤体承受自重能力与开采深度呈正比关系，故开采深度越大发生冲击地压的强度越高。

2)煤厚变化：煤层厚度变化位置的应力集中系数及弹性能都较大，因此冲击地压危险等级一定程度上取决于煤层厚度变化[6]。

3)最大主应力：最大主应力对冲击地压的发生具有控制作用，故矿井所处的构造应力场越强烈，表现出来的最大主应力对冲击地压发生的影响越严重[7]。

4)煤层倾角变化：煤层倾角变化反映煤层经历的构造运动强度，煤层倾角变化剧烈的位置多是构造运动剧烈的位置，诱发冲击地压的可能性必然较大。

5)与断层距离：断层等地质构造对冲击地压起到一定控制作用，故断层活化作用是诱发冲击地压的重要影响因素[8]。

6)顶板岩层厚度：顶板岩层厚度越大，断裂释放能量越大，发生冲击地压的危险程度越高[9]。

7)煤的坚固性系数：煤的坚固性系数是评价煤体抵抗载荷能力的重要指标，煤的坚固性系数越高，抗压能力越强，煤体发生冲击性破坏时释放的能量越大。

8)开采工艺：开采工艺不同，冲击地压诱发作用也不同，炮采对围岩扰动大于普采和综采，放顶式开采对围岩扰动大于一次采全高[10]。

9)顶板抗压强度：顶板岩石强度越大，断裂释放的能量也越大，诱发冲击地压的概率越高[11]。

10)底板抗压强度：底板岩层抗压强度对底鼓型冲击地压发生起关键作用，底板岩石强度越大，底板鼓起和破坏释放的能量越大[12]。

2 冲击地压分级预测原理

2.1 粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)是在搜寻范围内快速迭代寻求最优粒子的算法，并把寻优粒子当作优化问题的解。迭代过程中，两个“极值”不断变化，粒子随之不断更新，其中一个粒子作为已经搜索到的最优解p1，另一个粒子作为当前搜寻范围内的种群最优解p2。粒子的位置和速度随最优解不断更新，最终找到符合条件的最优解[13]。粒子寻优方式如下：

(1)

式中：vk为第k次偏移量；w为动量系数；c1、c2为搜索参数；r1、r2为修正系数；p1、p2为前后相邻两次迭代的最优解；xk为第k次迭代结果。

2.2 最小二乘支持向量机模型

最小二乘支持向量机(Least Squares Support Vector Machine，LSSVM)算法是对标准SVM算法的改进，LSSVM用等式约束和线性求解代替SVM中的不等式约束和非线性求解[14]，其算法过程如下：

假设有n个样本，则LSSVM描述的问题为：

(2)

式中：J为目标函数；w为样本权向量；ξ为样本松弛变量；t为惩罚因子。

LSSVM的Lagrange方程为：

(3)

式中：b为算式偏置；α为Lagrange乘子；φ(xi)为样本函数；xi为样本，i=1，2，…，n。

通过参数求解可得LSSVM决策函数g(x):

g(x)=sgn[αK(σ,f)+b]

(4)

式中：K(σ,f)为满足Mercer的核函数，K(σ,f)=φ(σ)φ(f)；σ、f为核函数的核参数和惩罚因子。

LSSVM核函数对预测模型起决定作用。选择径向基核(RBF)函数作为冲击地压预测的核函数，因为RBF函数结构简单、泛化能力强，能够满足对核参数σ和惩罚因子f的快速寻优。

2.3 PSO-LSSVM模型的预测流程

直接影响PSO-LSSVM预测模型精度的是RBF核参数和惩罚因子的选取。PSO算法能快速找到最优的核参数和惩罚因子，减少了繁琐的参数调整环节。PSO-LSSVM算法流程如图1所示。

图1 PSO-LSSVM算法流程

3 冲击地压分级预测实例

搜集多个矿区共计55组冲击地压历史数据，从中随机挑选40组数据作为本次预测的训练样本，其余15组数据为测试样本。训练样本中1～6组数据采集于大安山煤矿中区后槽，该煤层为急倾斜煤层，位于向斜构造附近，多次发生煤炮等动力显现；7～9组数据采集于木城涧煤矿+570 m水平，该区域为多煤层开采且间距小于30 m，顶底板为坚硬岩层，对煤层开采及巷道掘进影响较大；10～14组数据采集于忻州窑煤矿八采区，该区域煤层上覆留有煤柱，顶底板为坚硬岩层，具备较高的应力集中条件；15～19组数据采集于东滩煤矿六采区，该区域可采煤层范围不连续，褶皱与断层较发育，断层落差最大超过 50 m；20～25组数据采集于鲍店煤矿十采区，该区域回采时先采上部3上煤层后采下部3下煤层，3下煤层回采时直接顶裂隙发育，局部破碎严重；26～30组数据采集于红阳三矿西二采区，该区域开采深度超过1 000 m，顶板为坚硬特厚岩层；31～35组数据采集于红阳三矿西一采区，该区域整体上为相对孤立的块段，应力高度集中；36～40组数据采集于平顶山十矿二水平，该区域处于向斜构造轴部附近且断层较多，顶板断裂带范围较大，冲击危险程度高。预测指标体系中，不能量化的指标采用数字处理，例如煤厚变化程度采用数字“1”“2”“3”分别表示煤厚变化大、一般和小；煤层倾角变化用“1”“2”“3”“4”分别表示煤层倾角变化程度剧烈、严重、一般和基本无变化；普采、炮采和综采分别用“1”“2”“3”表示。训练样本和测试样本数据如表1和表2所示。

表1 训练样本数据

表1(续)序号开采深度/m煤厚变化/m最大主应力/MPa煤层倾角变化/(°)与断层距离/m顶板岩层厚度/m煤的坚固性系数采煤工艺顶板强度/MPa底板强度/MPa冲击等级40769223.1341591.622.2298.487.6Ⅲ

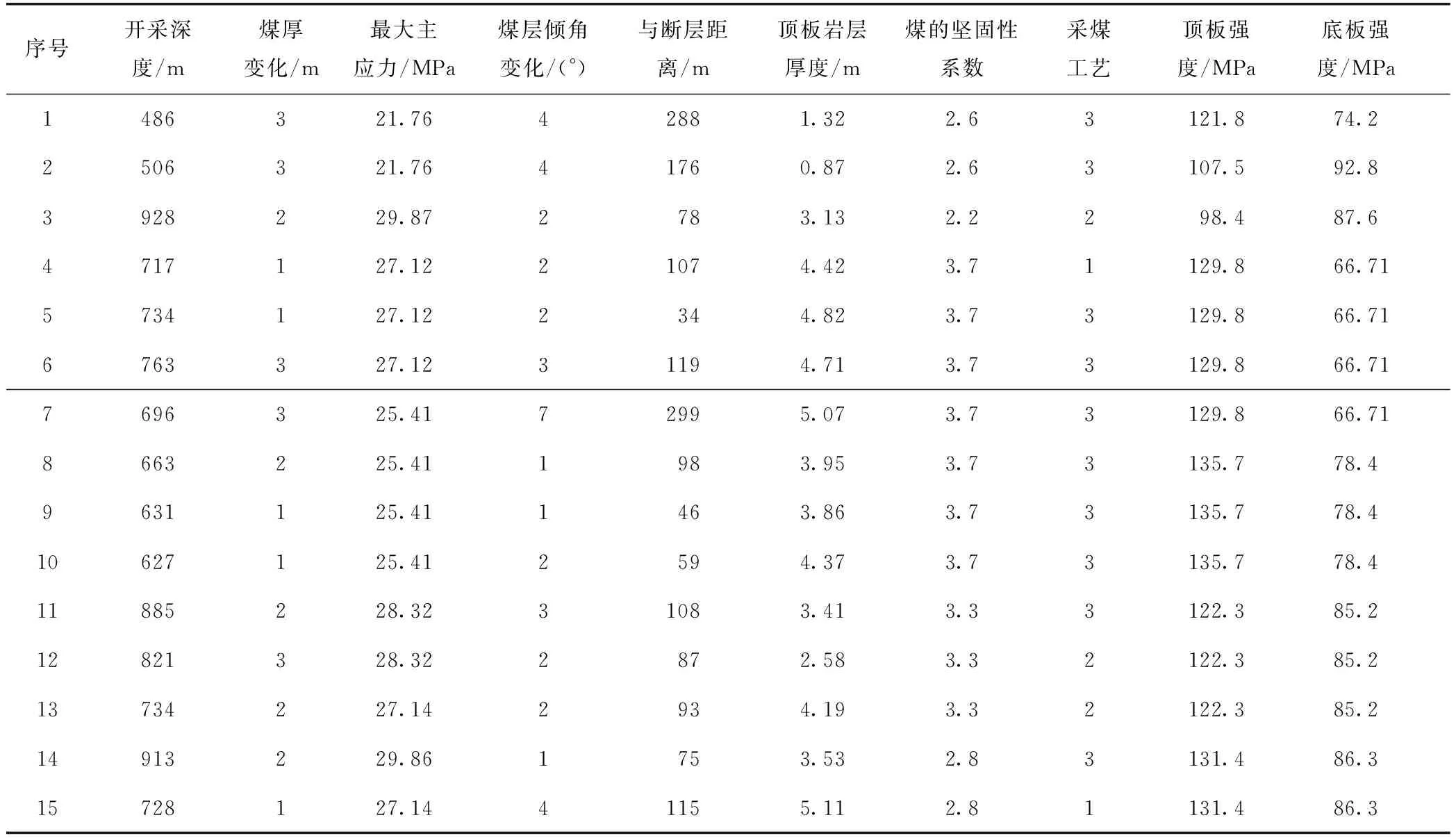
表2 测试样本数据

采用MATLAB2014b软件编写PSO优化程序源代码，借鉴文献[15]所述的参数设定方法，本次预测中将PSO模型参数设定如下：设定粒子群规模m=20，粒子向量维n=2，搜索参数c1=1.5，搜索参数c2=2，迭代次数设置为100。经运算得到惩罚因子f=119.736 2，核参数σ=19.158 4。再将其输入LSSVM模型中进行训练，待训练完成后将测试样本数据输入训练好的LSSVM模型中进行预测，LSSVM预测模型主要程序代码如下：

load data0.mat

[train_x,trps]=mapminmax(train_data′,0,1)

[test_x]=mapminmax(′apply′,test_data′,trps)

[train_y,tr1ps]=mapminmax(train_result′,0,1)

train_x=train_x′;train_y=train_y′

test_x=test_x′;bestmse=0.1

type=′f′;gam=500;sig2=0.45

kernel =′RBF_kernel′;proprecess=′proprecess′

model=initlssvm(train_x,train_y,type,gam,sig2,kernel,proprecess)

model=trainlssvm(model)

[train_predict_y,zt,model]=simlssvm(model,train_x)

train_predict=mapminmax(′reverse′,train_predict_y,tr1ps)

test_predict=mapminmax(′reverse′,test_predict_y,tr1ps)

trainmse=sum((train_predict-train_result).^2)/length(train_result)

testmse=sum((test_predict-test_result).^2)/length(test_result)

PSO-LSSVM模型预测结果如图2所示。可以看出，测试集预测结果与真实结果完全吻合，误判率为0，说明基于PSO-LSSVM的冲击地压分级预测方法准确率较高。

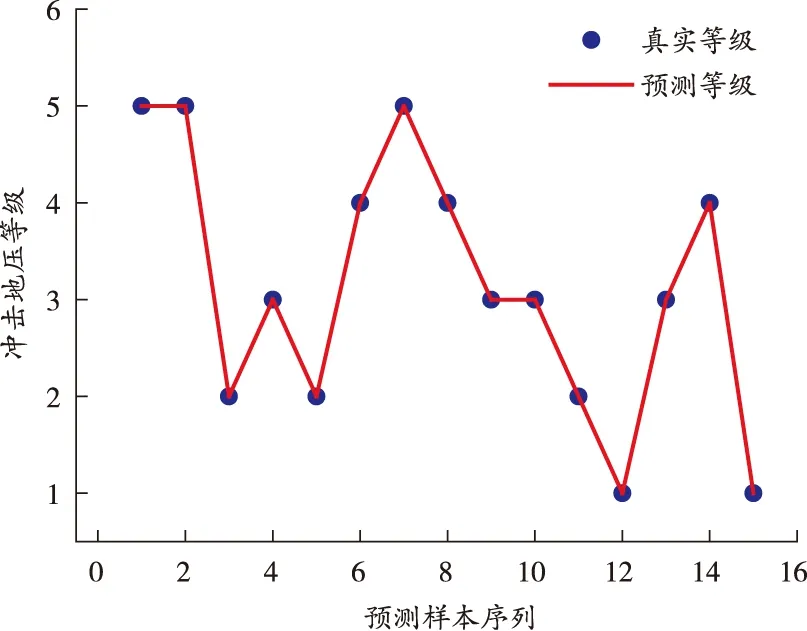
图2 PSO-LSSVM预测结果

为进一步确定PSO-LSSVM方法的准确性和实用性，将PSO-LSSVM方法的预测结果与BP、SVM、LSSVM和GA-LSSVM方法的预测结果进行对比，如表3所示。

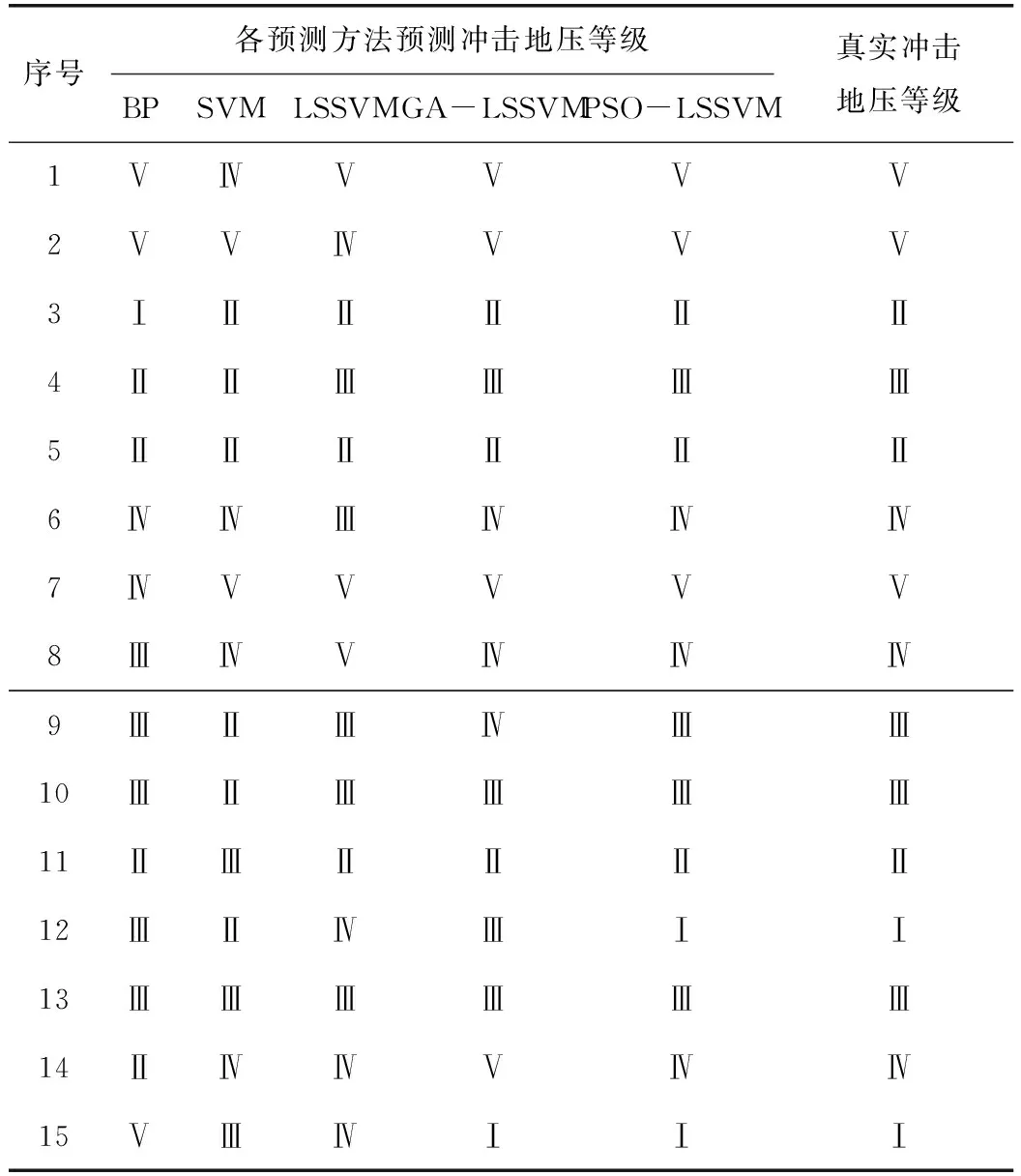
表3 预测结果对比

由表3可以看出，PSO-LSSVM预测未出现误判情况，其他4种预测方法都有一定的误判率，其中GA-LSSVM方法误判率为20%，LSSVM算法误判率为33%，SVM算法和BP算法的误判率都为47%。此外，PSO-LSSVM算法操作简便，只需将预测区指标参量输入模型，即可得到结果。实例分析表明，冲击地压分级预测的PSO-LSSVM方法最优。

4 结论

1)分析了冲击地压影响因素，提取10项对冲击地压发生起关键作用的影响因素，建立了冲击地压预测指标体系。

2) 采用PSO优化了LSSVM模型中的核参数和惩罚因子，在此基础上提出了冲击地压预测的PSO-LSSVM方法，并进行了实例预测。

3) 将冲击地压预测的PSO-LSSVM方法与BP、SVM、LSSVM、GA-LSSVM方法的预测结果进行了对比，表明PSO-LSSVM方法相较其他同类方法具有更高的预测精度。