递推法和数学归纳法在解决抽象概率计算中的应用
2021-02-14姜培华
姜培华 童 慧
(安徽工程大学数理与金融学院,安徽 芜湖 241000)
一、引言
概率论与数理统计(简称“概率统计”)是全国高等院校数学系与统计系的基础课,也是一些工科专业的数学类公共基础课。这门课的任务是以丰富的背景、巧妙的思维和有趣的结论吸引学者,使学生在浓厚的兴趣中学习和掌握概率统计的基本概念、基本方法和基本理论[1]。概率统计也是一门应用性极强的数学分支之一,它在工程技术、科学研究、经济管理、企业管理和经济预测等众多领域都有广泛的应用[2]。概率统计和其它数学分支有着紧密的联系(如数学分析、高等代数、实变函数和测度论等),是近代数学的重要组成部分。但这门学科的概念比较抽象,理论和方法具有很强的逻辑性,很多高校学生学习这门课程普遍感到比较困难。张德然和侯新昌分别在文献[3]和文献[4]中介绍了递推法在概率解题中的应用。旨在通过对一些抽象概率问题的计算进行剖析,展示如何利用全概率公式、递推法和数学归纳法来求解这类问题。通过对典型例题的分析、求解和方法凝练,加深学生对概率统计课程的认识,体验概率统计课程之中蕴含的“数学之美”,并在此基础之上开拓学生思维,激发学生学习兴趣,以期达到提高教学效果的目的。
二、相关知识
递推法和数学归纳法是解决数学问题的两大法宝,在求解复杂概率计算问题时,这两种方法一般不能单独使用,需要和全概率公式完美结合才能有效解决问题。全概率公式是概率论中一个重要公式,它提供了计算复杂事件概率的一条有效途径,使一个复杂概率的计算问题化繁为简、化难为易。下面我们简要给出递推法、数学归纳法和全概率公式的相关定义。
定义1 递推法[3]:在一个与自然数有关的问题里,通过寻找递推关系,由初始值递推获得所需结果的方法称为递推法。
定义2 数学归纳法:数学归纳法是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。除了自然数以外,广义上的数学归纳法也可以用于证明一般良基结构,例如:集合论中的树。这种广义的数学归纳法应用于数学逻辑和计算机科学领域,称作结构归纳法。

(1)全概率公式的最简单形式,设0 例1(结绳成圈问题) 将n根绳子的2n个头两两相接,求恰好接成n个圈的概率。 解 分析可知,如果已知一根绳子接成圈了,要使得n根绳子接成n个圈就等价于考虑剩下的n-1根绳子接成n-1个圈,如此下去很容易看出,利用条件概率会有一个明显的递推关系存在。为此,设事件An为“恰好接成n个圈”,记pn=P(An),又记事件B为“第一根绳子的两头相接成圈”,则由全概率公式可得 注意到 所以可得递推公式 由此可得 例2[5](交换抽球问题) 甲袋中有m-1个白球和1个黑球,乙袋中有m个白球,每次从甲、乙两袋中分别取出1个球并交换放入另一袋中去,这样经过了n次,求: (1)黑球仍在甲袋中的概率是多少? (2)讨论当n→∞时的情况下,黑球仍在甲袋中的概率是多少? 解 (1)设事件An为“经过n次交换后,黑球出现在甲袋中”,记pn=P(An),当n≥1时由全概率公式可得 注意到 所以可得递推公式 又因初始条件p0=1,由递推关系并利用等比级数求和可得 例3(轮流掷骰子问题) 甲、乙两人轮流掷骰子,先由甲掷。每当某人掷出1点时,则交给对方掷,否则此人继续掷。试求第n次仍由甲掷的概率。 解 设事件Ai为“第i次由甲掷骰子”,记pi=P(Ai),i=1,2,…,由全概率公式可得 注意到 可得 由此可得递推公式 将初始条件p1=1,带入上式可得 例4(天气预测问题) 假设天气变化只有两种情况:有雨或无雨。若已知今天的天气情况,明天天气保持不变的概率为p,改变的概率为1-p.设第一天无雨,试求第n天也无雨的概率。 解 设事件A1为“第i天无雨”,记pi=P(Ai),i=1,2,…,由全概率公式可得 注意到 p(An|An-1)=p, pn-1+(1-p)(1-pn-1=(2p-1)pn-1+(1-p),n≥2 可得 pn=ppn-1+(1-p)(1-pn-1) =(2p-1)pn-1+(1-p),n≥2. 由此可得递推公式 将初始条件p1=1,带入上式可得 以上例子之所以能够利用递推法求解,一则因为随机试验与自然数有关, 二则由题意可知其前后试验具有密切的关联性。因而可断定它们必存在某种内在联系,这就是能用递推法求解的根本所在。但不同的是,利用全概率公式在寻找递推关系时,对“条件事件”的选取要因题而异,值得思考和辨析。在有些情况下, 由于试验比较复杂 直观看前后次的试验有关系,但获得递推关系式难度较大,有时即使获得了递推关系式, 式中仍参差杂着其它未知参数,这就需要我们从纷繁复杂的事件关系或初始条件中设法确定出此参数,否则,递推公式就失去了意义。 通过例子1-4的分析,利用递推法求解抽象概率问题需要注意下述三点: (1)恰当选择“条件事件”是基础。如:例1 是对“初次事件B”取条件,而例2-4是对“相邻事件An-1”取条件,恰当选取“条件事件”很重要,否则后面的“条件概率“不易求出,进而影响着能否顺利解决问题。 (2)“条件概率”的计算是难点,它是利用全概率公式寻求递推关系的前提。 (3)利用递推关系,结合初始概率p1最终求解是关键。 例5(循环取球问题) 有个口袋,每个口袋中均有a个白球、b个黑球。从第一个口袋中任取一球放入第二个口袋,再从第二个口袋中任取一球放入第三个口袋,如此下去,从第n-1个口袋中任取一球放入第n个口袋。最后从第个口袋中任取一球,求此时取到的球是白球的概率。 pk=P(Ak) 故由归纳法可知: 例6(抽球出现早晚问题) 口袋中有a个白球、b个黑球和n个红球,现从中一个一个不放回地取球。证明:白球比黑球出现早的概率为a/(a+b),与n无关。 解 记事件A为“第一次取出白球”,B为“第一次取出黑球”,C为“第一次取出红球”。易知,事件A,B,C互不相容,且A∪B∪C=Ω.又设En为“有n个红球时,白球比黑球出现得早”,记pn=P(En),下面对n用归纳法: pn=P(A)P(En|A)+P(B)P(En|B)+P(C)P(En|C) 注意到P(En|A)=1,P(En|B)=0,P(En|C)=P(En-1)=pn-1,代入可得: 由归纳法可知,结论成立。 例7[6](波利亚坛子问题) 设一坛子装有b个黑球、r个红球,任意取出1个球,然后放回并再放入c个与取出的颜色相同的球,证明: (1)任一次取出黑球的概率是b/(b+r),任一次取出红球的概率是r/(b+r),与n无关; pk=P(Ak) 事实上,我们把k次取球分为两段:第1次与后面k-1次取球。当第1次取到黑球时,罐中增加c个黑球,这时从原罐中第k次取到黑球等价于从新罐(含b+c个黑球,r个红球)中第k-1次取到黑球,故有 (2)先证当m=1时,对一切n(n>m)命题成立。设Bj为“第j次取到黑球”,由结论(1)得: P(B1Bn)=P(B1)P(Bn|B1) 这表明当m=1时,对一切n(n>m)命题成立。 设m=k-1时对一切n(n>m)命题成立,现证明m=k时对一切n(n>m)命题仍然成立。 因为 事实上,概率P(BkBn|B1)等于从装有b+c个黑球和r个红球的袋中第k-1次与第n-1次都取得黑球的概率,由归纳假设得 同理有 由归纳法知,结论成立。 通过对例子5-7的分析,利用数学归纳法求解抽象概率问题需要注意下述两点: (1)恰当选择“条件事件”是基础。如:例6和例7 是对“初次事件”取条件,相反例5是对“相邻事件Ak-1”取条件,恰当选取“条件事件”至关重要,否则后面的“条件概率”不容易求出,进而影响能否顺利解决问题。 (2)“条件概率”的计算是难点(某些情况下很抽象,不容易求出,如例7),它是利用全概率公式和归纳假设顺利解决问题的的关键。 总之,古典概率的计算一直是概率统计中的一个重点和难点问题,其方法灵活,技巧性强,学生难于掌握。抽象概率问题的计算更为困难,其一,问题叙述一般比较抽象复杂,整个事件的发展变化过程不太直观;其二,所求解的概率问题往往都与“次n数”有关,大都具有不确定性,很难一一枚举列出。通过文中的典型实例分析,不难发现,处理这类抽象概率问题时,如果能够把递推法、数学归纳法和全概率公式巧妙结合起来,会有效解决问题,具有“事半功倍”的效果。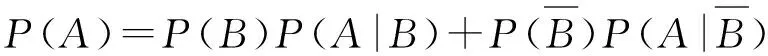

三、递推法求解抽象概率问题举例





四、用数学归纳法求解抽象概率问题举例

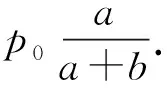
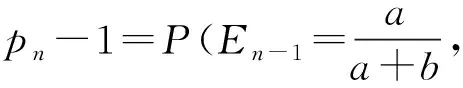





五、结语
