基于COMSOL的线性压缩机动力学仿真与实验验证

孔家煊，赵钦宇，晁春阳，周文杰，王 博，程 路，甘智华*，徐 军

（1.浙江大学制冷与低温研究所 浙江省制冷与低温技术重点实验室，杭州 310027；2.杭州电子科技大学能量利用与自动化研究所，杭州 310018；3.日照华斯特林科技有限公司，山东 日照 276800）

0 引言

近年来，由于红外技术和超导领域的持续发展，低温制冷机的需求日益增长[1−2]。斯特林制冷机作为低温制冷机的重要分支，具有本征效率高、稳定性好、结构紧凑和使用寿命长等优点。斯特林制冷机的驱动源是高频的交变压力，压缩活塞和气缸间的侧向力不利于延长寿命和减小噪声，因此使用直线电机驱动压缩机，不但可以省去运动转换装置；同时能通过调节电压来调节活塞行程[3]。

建立合理的数值模型对斯特林制冷机以及线性压缩机的设计非常重要，许多研究者已经开展了相关工作。Clark将线性压缩机的机械常量、电参数、动子质量等效到一个电路等效模型中，以匹配一台斯特林制冷机为例，通过非线性静磁场的有限元方法，以最小线圈电阻损耗和最小设备体积为目标，对线性压缩机进行了设计[4]。Almajri等[5]用COMSOL建立了斯特林制冷机的计算流体力学（CFD）模型，通过实验验证后使用该模型研究了相角、孔隙率、回热器长度对制冷量的影响。上海技术物理研究所的邓伟峰等[6]采用Maxwell建立了自由活塞式线性压缩机电磁−机械−声耦合模型，模拟了不同负载条件下压缩机电磁参数和动力特性的瞬态变化规律。

目前，在回热式低温制冷机设计领域，一维数值计算软件SAGE在制冷机端较为完善，而在压缩机端仅提供了几个简单的接口，简化了电磁场的计算[7]，无法对压缩机的设计起到良好的指导作用。为了弥补SAGE在压缩机建模上的不足，本文采用COMSOL对线性压缩机进行建模仿真，并通过实验对仿真模型进行验证，以期为线性压缩机的设计和优化改进提供一种简易有效的方案。

1 建模

高频回热式低温系统中各状态量在时域中都可看作交变的正弦波[8]，基本的表示形式为：

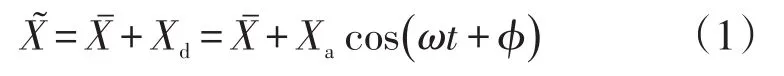
利用欧拉公式改写式中动态项Xd：

其中：表示交变的物理量，可根据正弦波的定义将其分解为Xˉ与动态Xd。对于制冷系统，运行过程中存在多个交变量，在时域中无法直观的表现各物理信号之间的关系。一种更常用且直观的做法是将时域上的交变信号映射到频域中。在复平面中，动态项映射的结果是以幅值Xa为长度，ωt+φ为方向的向量。

基于以上原理，在复平面内建立压缩活塞的质量−弹簧−阻尼模型，该模型在复平面中某一时刻的受力分析如图 1 所示[9]，其中点折线箭头表示此时刻位移、速度和加速度的相位，实线箭头表示压缩活塞在工作状态下所受的力，表示电机推力，表示弹性力，表示惯性力，表示阻尼力，表示气体力。

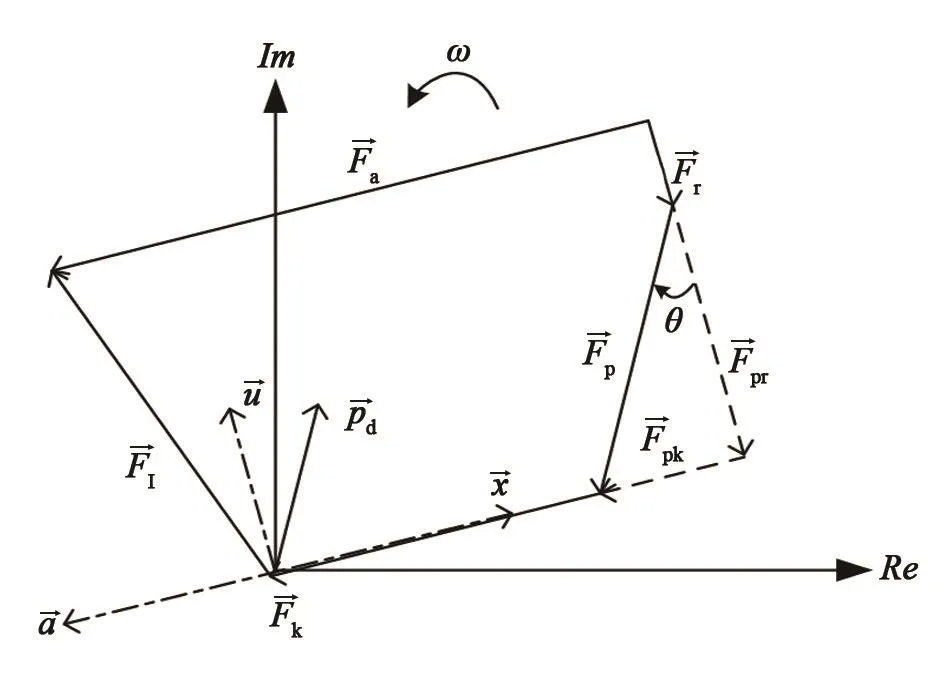
图1 复平面活塞受力分析图Fig.1 Force analysis of piston in the complex plane

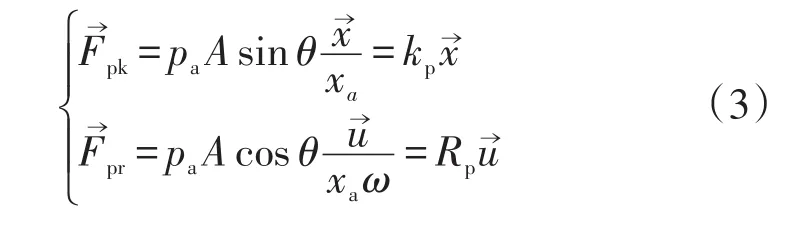
式中：pa和xa分别为压力和位移在时域中的幅值，A代表活塞截面积；ω为线性压缩机的角频率；θ为回热器热端质量流领先压力波的相位角，对于斯特林制冷机，实际设计中应将其控制在40°至45°，从而减小回热器损失；kp和Rp为合并常数项后的结果，分别代表气体弹性刚度和气体阻尼系数。二者表征了制冷机侧对线性压缩机的影响，通过改变压力幅值和相位角可以模拟压缩机在连接不同工况制冷机时的运行情况。

COMSOL是一款基于有限元方法的多物理场仿真软件，通过其内置的模块可以便捷地实现对电磁学、流体流动、传热学等领域的仿真和对不同物理场的耦合。本文采用COMSOL对一款商用Cryo S 100斯特林制冷机动磁式线性压缩机工作过程中的电磁场及压缩机在电磁场中的运动状况进行了动态分析。

线性压缩机的装配模型与仿真模型的对应关系如图2所示，运动活塞由板弹簧支撑，与气缸内壁形成间隙密封；永磁体2是活塞的一部分，位于内定子1和齿形磁轭3之间的气隙内。当齿形磁轭包裹的线圈4中通入正弦电流时，永磁体会受到交变的轴向电磁力从而带动活塞做往复直线运动。

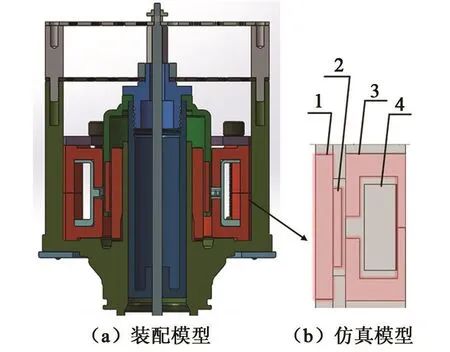
图2 线性压缩机装配模型与仿真模型对照图Fig.2 The assembly model and simulation model of linear compressor

建立仿真模型的参数如表1所示。为了提高计算效率，对装配模型进行以下的假设和简化：

（1）忽略模型在径向上的运动；

（2）简化活塞的完整形状，将所有的质量和受力集中到永磁体上；

（3）假定板弹簧对活塞提供的轴向力与位移是线性相关的，且摩擦因素被简化为固定的机械阻尼系数；

（4）使用相对磁导率为1的气体介质填充模型组件以外的区域。

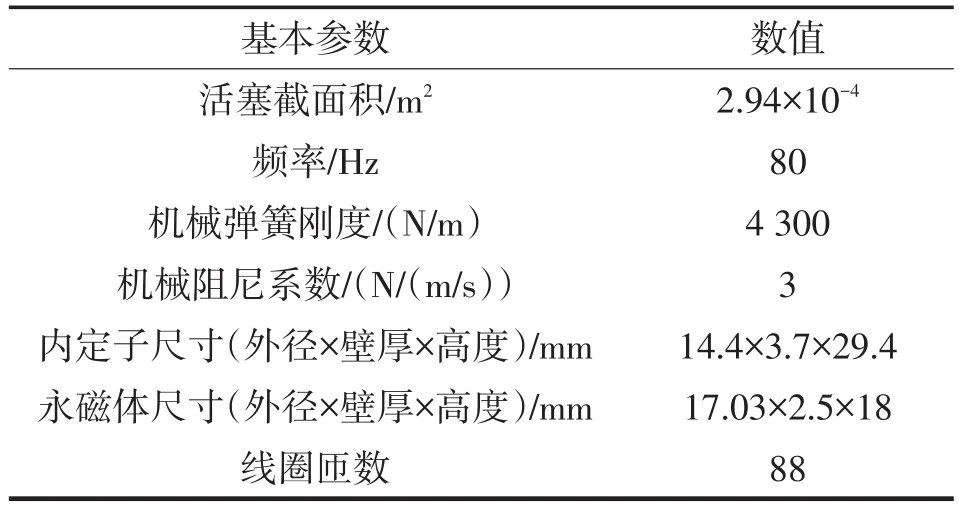
表1 线性电机的基本参数Tab.1 Primary structure parameter of linear motor

使用不同的磁性本构关系描述磁场中软磁材料和永磁体的磁性特征。对于内定子和磁轭使用的Somaloy软磁材料，通过导入图3所示的外部的材料磁化属性表，对其磁性能进行了描述。对于永磁体，指定了剩余磁感应强度关系式，如式（4）所示，其中表示剩余磁感应强度，μ0表示真空磁导率，μr表示永磁体的相对磁导率，表示径向矫顽力。对应该系统中使用的永磁体，μr=1.02，

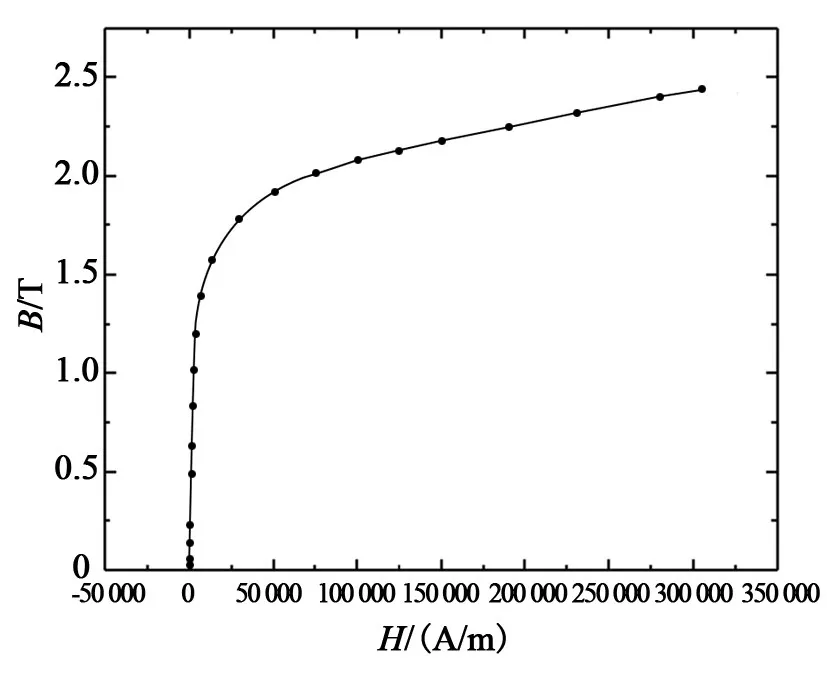
图3 软磁材料B-H曲线Fig.3 B-H curve of Somaloy

根据图1，使用“全局常微分和微分代数方程”接口导入带气体力的运动方程描述活塞的机械运动。电磁场和运动方程通过位移量x和电磁力FI相互耦合，在线圈内指定输入电流，可以求解电磁力、位移量和速度量随时间的变化关系。

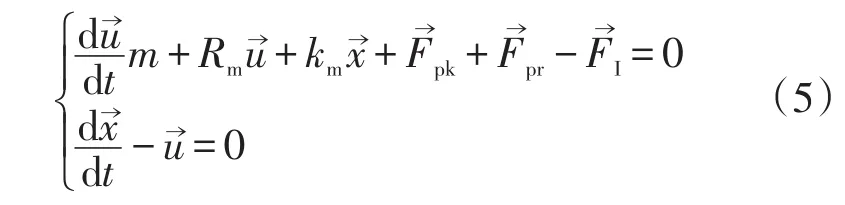
为仿真模型添加移动网格时，考虑到运动部件只有活塞，可以将模型如图4所示分为内定子、永磁体和包裹线圈的磁轭三个部分。仅在中间的永磁体区域使用移动网格接口。在该区域内，将图4中红色线框所包裹的永磁体和其周围的一部分气体作为整体，指定其轴向位移为微分方程接口求解得到的位移量x，上下方的气体域设置为被动变形的自由变形域，并使用了映射网格来减少由于网格划分带来的计算误差，防止发散。

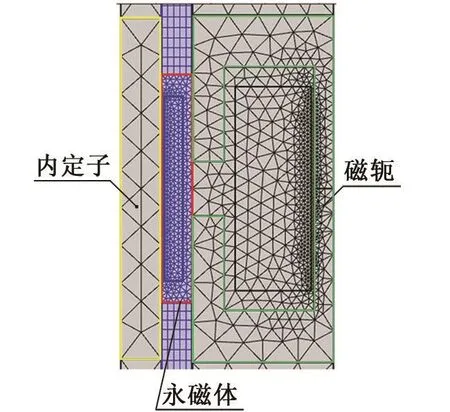
图4 模型网格剖分Fig.4 model meshed geometry

电磁场的模拟必须使用麦克斯韦应力张量对活塞受到的电磁力进行精确的求解，因此在永磁体和气隙部分绘制了更为精密的网格。同时为了更好地保证移动域和非移动域之间物理量的连续性，在二者相交的边界上，移动域一侧必须进行更精细的边界单元划分。最终网格的平均质量为0.82。经无关性验证，进一步加密网格对求解结果的影响不超过5%，求解器步长设置为0.001 s。

2 实验流程

2.1 空载实验装置

图5为测试空载工况活塞位移的装置示意图，线性压缩机由变频电源驱动，可直接读出输入电压、输出电流和有效功率；压缩机活塞板簧轴向上方装有激光位移传感器，能对活塞板弹簧的运动进行实时测量，活塞板弹簧的中心孔通过紧固螺母和活塞相连接，二者的运动始终具有一致性；在空载条件下设置输出电压和频率为80 Hz、7 V，记录此时压缩机活塞的位移结果，与仿真结果进行对比。

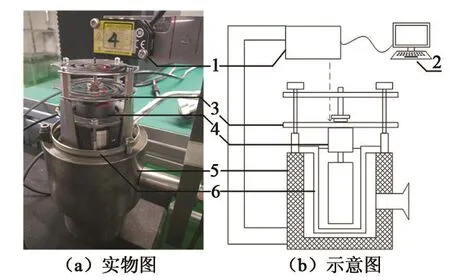
图5 空载工况下活塞位移测试装置实物图和示意图Fig.5 Physical diagram and schematic diagram of piston displacement test device under on-load condition

2.2 比推力实验装置

将压缩机直线电机平稳放置在拉压力测试仪的托盘中心。直线电机由直流电源驱动，可以直接读出输入电压和输入电流；拉压力测试仪在压缩活塞轴向上方连接有压力触头，可以通过手轮控制的限位机构精确限制压缩活塞的位置，并对活塞的推力进行测量。

测量时，设置直流电源输出电流依次为1 A、2 A、3 A、4 A、5 A；记录活塞在不同限位条件下推力与电流的变化关系，从而对仿真结果进行对比验证。

3 讨论

3.1 空载实验

在模型中输入与实验相同的空载工况，对活塞的位移情况进行了计算。采用测试装置对多台压缩机进行了空载测试，测试结果如图6所示。在随机抽取的50台线性压缩机中，有四台压缩机的活塞位移与计算值出现较大偏差，其余样机的测试结果平均分布在计算值附近。进一步比较后发现，出现较大偏差的四台线性压缩机的活塞与排出器之间的位移相位差远大于其余线性压缩机的位移相位差，推测是在装配过程中零件安装不当产生的影响。剔除错误样本后，测试值与计算值的平均偏差为3.49%。

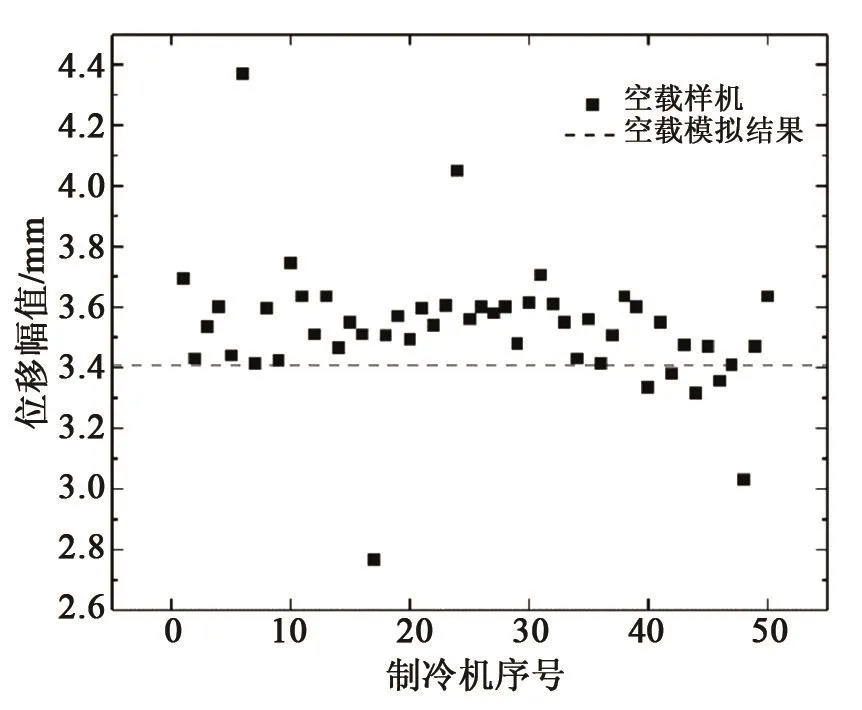
图6 空载工况下活塞位移的结果分析图Fig.6 The result of displacement in no-load condition

3.2 比推力测试

在SAGE模型中，压缩机端的影响是通过指定比推力引入的，为验证压缩机模型的合理性，使用前文所述测量方式，依次测量了活塞在距离平衡位置0 mm、1 mm、2 mm、3 mm、4 mm处的比推力。同时在模型中将压缩活塞的永磁体固定在对应的位置，设定线圈的电流参数，从稳态的角度对压缩活塞在不同位置上的比推力进行求解，结果如图7所示，实测值略大于计算值，最大偏差出现在离初始位置1 mm处，为7.2%；最小偏差出现在离初始位置4 mm处，为4.37%，无论是实测值还是计算值，比推力的最大变化不超过0.4 N∕A。在模型中进一步增大与初始点的距离后，发现当压缩活塞位移超过6 mm时，活塞会由于逐渐脱离线圈生成的磁场，导致比推力迅速衰减。

3.3 负载条件下与Sage模型比较

该模型中，制冷机侧的影响被简化为气体力，为了验证这种方法的可行性，使用SAGE模型计算了该款制冷机在100 K、193 K、253 K和293 K四个工况点下的动态压力幅值、压缩机出口的压力−质量流相位、阻抗等参数，将它们换算为气体力的形式输入COMSOL模型进行计算，并对比了用两种模型计算的活塞位移幅值。该制冷机使用表1所列的线性电机。计算结果如图8和表2所示，在不同的冷头极限温度下，对压缩活塞位移的计算结果均吻合的较好，最大偏差不超过3%。

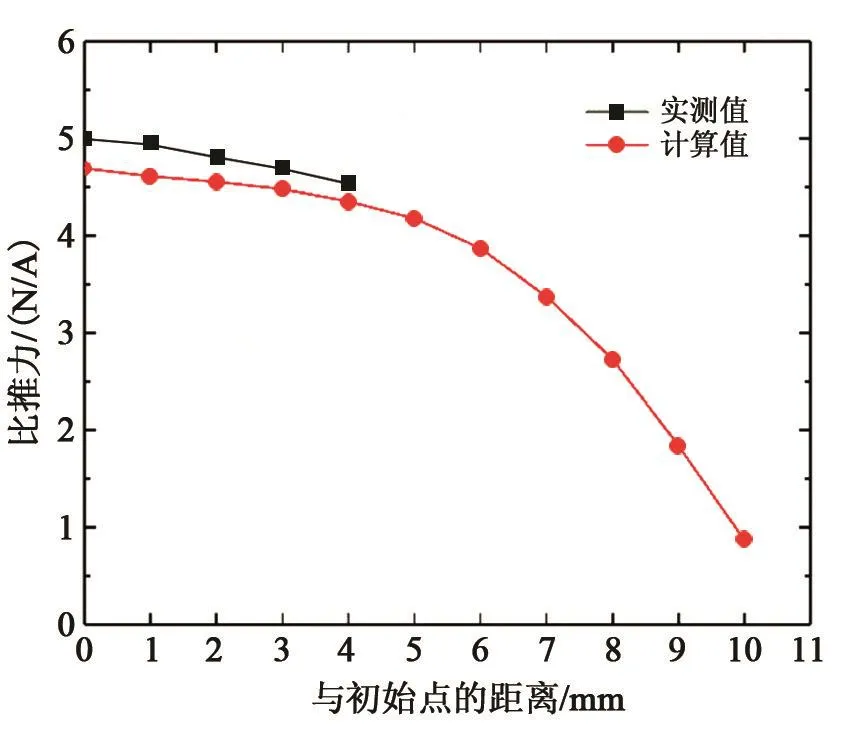
图7 比推力随位移的变化关系比较曲线Fig.7 The measurement and simulated result of specific thrust vs.displacement

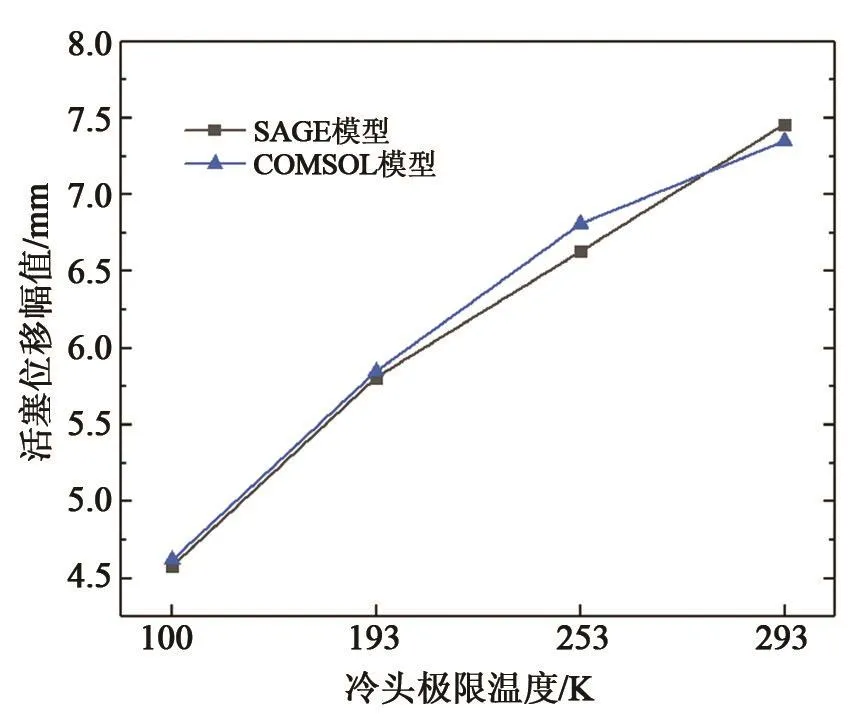
图8 两种模型计算结果对比曲线Fig.8 Comparison of displacement in two models

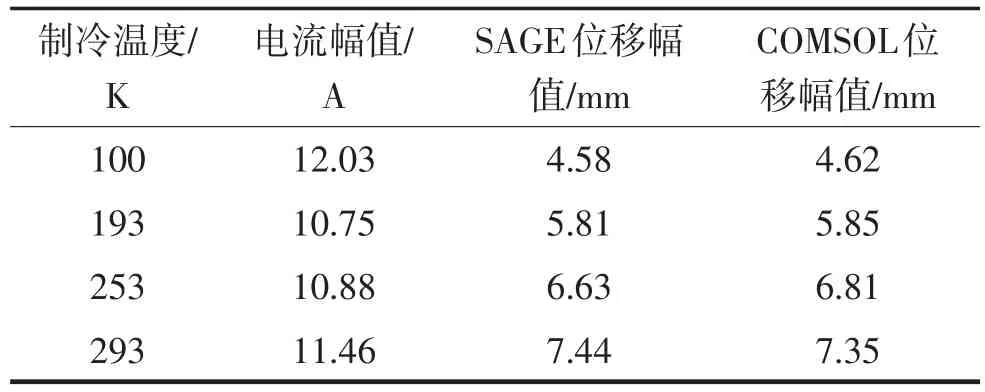
表2 基于压力幅值的位移幅值比较结果Tab.2 Comparison of displacement base on pressure amplitude

4 结论

本文基于斯特林制冷机电−机械−声的耦合原理，将声阻抗拆分为位移和速度方向分量，建立了带负载条件的直线电机COMSOL模型，并进行了空载测试、比推力测试和与SAGE模型的对比验证。其中空载测试的50台电机中，测试值与计算值的平均偏差为3.49%；对位于磁场不同位置处活塞的比推力测试表明，测试值和计算值的最大偏差出现在距离平衡位置1 mm处，为7.2%，最小偏差出现在距离平衡位置4 mm处，为4.37%。计算结果表明，当压缩活塞距离平衡位置6 mm以上时，比推力将迅速衰减；在不同负载条件下，该模型的活塞位移计算结果和SAGE的计算结果均吻合良好，最大偏差不超过3%。