感压膜片预张力对电容薄膜真空规输出特性的影响

贾春旺，陈叔平*，成永军，孙雯君，裴晓强，孟 岳，金树峰，杨 雯，赵高逸

（1.兰州理工大学石油化工学院，兰州 730050；2.兰州空间技术物理研究所，兰州 730000）

关键字：电容薄膜真空规；感压膜片；预张力；有限元分析；输出电容

0 引言

随着我国科学技术的发展，科学试验和生产工艺对真空测量准确度的要求越来越高，这对真空度测量与校准提出了更高的要求，准确测量真空度显得尤为重要[1]。电容薄膜真空规（CDG）相比其他试件模型，具有使用方便、延迟小、精度高、测量结果与气体种类无关、重复性能好的优点[2]，作为中、低真空测量最重要的真空规之一，被广泛用于航空航天、工业生产、重大科学仪器等领域的低真空测量，并可作为粗低真空的副标准和传递标准[3−5]。

对于薄膜器件，使用中若不施加或施加较低数值的预张力，会导致薄膜出现褶皱，承载后易出现变形过大的现象，并且在外界激励作用下，容易发生振动；而预张力过大，会增加安装难度，薄膜承载后，会造成应力过大等缺点。因此，为保证薄膜的平整度及承载能力，增加其稳定性，往往先使薄膜受到均匀的张力，然后再对其边缘加以固定[6]。感压膜片是电容薄膜真空规的核心部件，通常具有较大的宽厚比[7]，安装时亦须施加预张力。预张力大小会影响感压膜片的挠度，进而影响真空规的输出特性，因此，必须考虑预张力对真空规性能的影响问题。

本文以电容薄膜真空规电容感应模块为研究对象，结合COMSOL Multiphysics软件及电容器电容理论计算方法，对受预张力的感压膜片所构成的电容感应模块进行建模分析，研究预张力对电容薄膜真空规输出特性的影响，为后续的研究及设计提供一定的参考。

1 理论模型

图1为电容薄膜真空规基本结构。主要由进气管、感压膜片、固定极板、固定基底、外壳体等组成。感压膜片与进气管连接一侧为测量室，另一侧为真空腔。

电容感应模块主要包含感压膜片、固定极板及真空腔，感压膜片为上极板，固定极板为下极板，两极板间为真空状态。电容薄膜真空规基于变极距式平行板电容器结构制作，当感压膜片受到压力p作用时发生形变，导致两极板初始间距d减小，电容增大，电容值与压力一一对应，通过电容检测电路检测微小电容变化量，然后使用适当的测量转换电路将电容的变化转换为电压信号，完成压力的测量[8−9]。

1.1 初始电容

初始电容是指无外界压力作用时电容薄膜真空规输出的电容值，此时，感压膜片挠度为零，与固定极板平行。电容按平行板电容器计算，表达式为：

式中：C0为初始电容，pF；ε0为真空介电常数，数值为8.85×10−12F∕m；b为固定极板半径，mm。

1.2 可变电容

当受到外界压力作用时，感压膜片发生形变，致使两极板间距减小，输出电容发生变化。膜片的形变遵循一定的挠度曲面方程，设膜片位于r，θ平面，膜片形变后与固定极板之间的电容可按下式计算：

式中：C为可变电容，pF；εr为介质的介电常数，真空条件下εr=1；S为极板相对面积，mm2；r为膜片中心到膜片上任意一点的距离（0≤r≤b），mm；ω（r）为膜片变形后的挠度轮廓，可根据挠度形状函数确定[9]：

式中：ω0为膜片中心挠度，mm；a为膜片半径，mm。

将式（3）代入式（2）得：

由上式可知，计算可变电容不仅要知道真空介电常数、极板相对面积与极板间距，还须知道感压膜片的中心挠度。施加预张力的感压膜片在均布载荷作用下其中心挠度可由式（5）求得[10]：

式中：p为薄膜所受压力，Pa；E为弹性模量，GPa；μ为泊松比；t为薄膜厚度，mm；σ0为施加于感压膜片的预张力，MPa。

2 电容薄膜真空规输出电容仿真

电容薄膜真空规的输出电容仿真包含了电场和力场两个物理场，必须通过耦合场来分析，与其他有限元分析软件相比，COMSOL专注于多物理场耦合的建模与仿真，将多个物理场封装成不同的模块，使得分析结果更加贴近实际。选择COMSOL中的机电模块（emi）建立几何模型，它同时包含了静电场、力场和移动网格功能，无须考虑各个物理场之间的耦合。与理论计算过程相比，COMSOL仿真能同时获得输出电容、电势分布、挠度分布、应力应变分布等结果，并且能够很好地解决感压膜片在压力作用下的非线性问题。本文所建的几何模型分为三部分：感压膜片、真空腔和固定极板。

2.1 模型建立

以现有的测量上限为1.33 kPa的电容薄膜真空规为对象，取感压膜片直径为72 mm，厚度为45μm，材料选用Inconel 600合金；固定极板直径为39 mm，厚度为3μm，材料选用Ag；两极板间距为250μm。可变电容仿真主要涵盖力场和电场，设置材料的弹性模量、密度、泊松比及相对介电常数，由于电容值的大小与两极板介电常数无关，故对两极板介电常数不作设置，表1为材料参数。采用用户控制网格方式建立网格划分模型，通过设置单元最大尺寸，形成扫掠网格。该有限元模型主要以六面体网格为主，网格单元数为68 429，结点数为98 713，电容感应模块的网格划分模型如图2所示。

表1 电容感应模块材料参数Tab.1 Material parameter of capacitive sensing module

图2 电容感应模块网格划分模型Fig.2 Mesh model of capacitive sensing module

2.2 边界条件

针对上述网格划分模型，应用COMSOL软件机电模块模拟施加预张力的感压膜片输出电容随压力的变化。边界条件分为力场边界条件与电场边界条件，力场边界条件包括约束与载荷的大小及位置，电场边界条件包括终端电势与接地设置。对于施加预张力的感压膜片，张拉膜片的外边界是获得均匀张力的有效方法，在膜片外边界施加指定位移约束，将预张力等效为膜片的径向位移。在薄膜上下两侧施加压力，一面为待测压力，一面为参考腔压力。理论情况下，参考腔为真空状态，但实际情况下，由于材料表面的气体附着及长时间静置，腔体会有一定程度漏气，故参考腔压力一般维持在10−4Pa。在压力作用下感压膜片中心挠度远大于膜片厚度，为大挠度模型，故在分析前启用非线性命令，以准确描述膜片在大挠度情形下的应变情况。将感压膜片接地，电势为0 V，设置固定极板终端电压为10 V，两者构成电容器。

3 结果分析

3.1 不同预张力下输出电容

为便于分析预张力对输出电容的影响，分别对感压膜片施加30 MPa、40 MPa、50 MPa、60 MPa、70 MPa的预张力。针对每组预张力，在0～1 330 Pa内，以0 Pa为起点，133 Pa为步长，选取10组待测压力分别施加于感压膜片，并通过理论计算，得到不同预张力下输出电容的理论解，并与COMSOL软件求得的仿真解进行对比验证。不考虑寄生电容及电场边缘效应的影响，仿真所得到的不同预张力下输出电容的仿真解（C1、C2、C3、C4、C5）与用式（4）求得的理论解（C1′、C2′、C3′、C4′、C5′）对比，并求得相对误差（δ），如表2所列。当待测压力为0 Pa时，输出电容为初始电容，仿真结果为42.88 pF，通过式（1）求得的理论结果为42.27 pF，相对误差为1.44%。

由表2可知，当待测压力变化时，输出电容仿真解与理论解的最大误差为16.6%，最小误差为2.2%，总体表现为压力越大，相对误差越大；预张力越大，相对误差越小的趋势。这是由于在电容理论计算式中，电容的准确计算取决于挠度形状函数的准确性，而式（3）所示的挠度形状函数为近似函数，只能近似描述预张力膜片的挠度分布；另一方面是由于压力越大，膜片非线性形变越大，而仿真计算过程中网格数量有限，计算精度下降，故产生累计误差。

仿真同时得到了不同预张力下感压膜片的中心挠度，与用式（5）求得的理论解对比，挠度的最大误差为7.1%，最小误差为2.5%，总体表现为压力越大，相对误差越小的趋势。综上所述，所建立的有 限元分析模型合理可用。

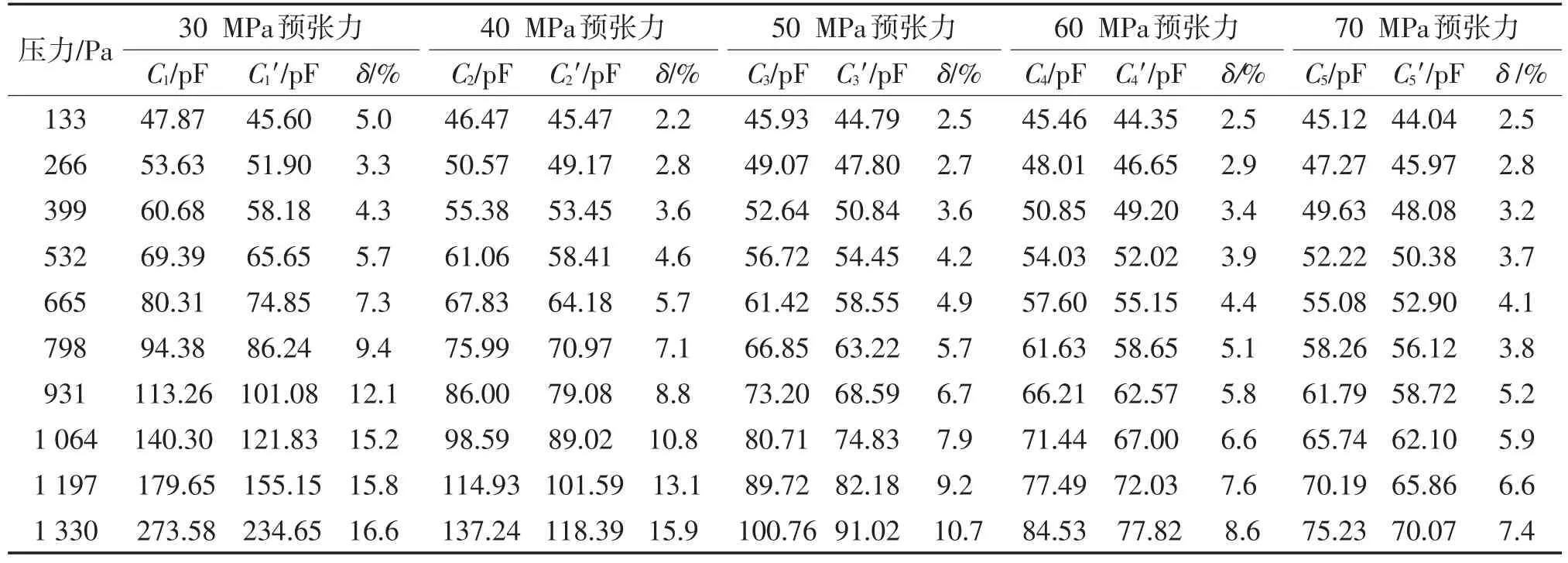
表2 不同预张力情况下输出电容比较Tab.2 Comparison of output capacitance under different pretensions

图3、图4分别为不同预张力下感压膜片中心挠度及输出电容随压力的变化曲线。由图3可知，感压膜片中心挠度随压力呈非线性增大；预张力增大，中心挠度减小。

图3 不同预张力下感压膜片中心挠度随压力的变化曲线Fig.3 The curve of center deflection with pressure under different pretensions

由图4可知，同一预张力下，随待测压力的增大，输出电容增大。同一压力下，增大预张力会导致输出电容减小，减小幅度随预张力的增大而逐渐降低。随预张力的增大，输出电容−压力曲线逐渐趋于线性。压力大于1 000 Pa时，单位压力下输出电容增量快速增大，特别当预张力为30 MPa时，增长最为明显，这是由于等效电极距离减小、速度加快所致。在实际使用中，要尽量避免待测压力值接近真空规量程上限。

图4 不同预张力下输出电容-压力特性曲线Fig.4 Output capacitance-pressure characteristic curve under different pretensions

3.2 预张力对真空规性能的影响

真空规的性能评价指标主要有灵敏度、线性度、分辨率、迟滞差、重复性及稳定性等，预张力主要影响其线性度及灵敏度。真空规灵敏度的定义为，稳态工作下，输出变化量与输入变化量之比，用S表示。理想情况下，真空规的输出特性曲线为一条直线，灵敏度是一个常数，但在实际过程中，输出特性曲线并非直线，每点的灵敏度均不同。因此，在实际计算中，灵敏度可以用近似直线的斜率来表示，即S=ΔC∕Δp，ΔC为量程内输出电容的变化量，Δp为待测压力的变化量。采用最小二乘法分别对各预张力下的电容−压力特性曲线进行拟合，拟合后得到的拟合直线与原特性曲线的电容最大偏差与满量程输出电容的百分比，即为真空规的线性度。不同预张力下真空规的灵敏度与线性度如表3所列。

表3 不同预张力下电容薄膜真空规的线性度及灵敏度Tab.3 Linearity and sensitivity of capacitance diaphragm gauge under different pretensions

由表3可知，感压膜片预张力增大，真空规的线性度提高，但灵敏度降低，故在真空规其他结构尺寸确定的情况下，必须准确控制薄膜预张力的大小，使其灵敏度与线性度均表现良好。预张力过大，会使真空规灵敏度变差，导致其对微小压力的变化感知不灵敏，造成测量结果不准确；而预张力过小，会使真空规非线性误差增大，稳定性变差，并增加后续信号处理及电测线路的设计难度。对于有限元模型，当预张力为50 MPa，气压在0～1 330 Pa内变化时，输出电容的变化为42.88～100.76 pF，真空规的线性度为7.3%，灵敏度为0.0433 pF∕Pa，后续通过电路补偿可进一步提高线性度。文献[3]中设计了一种基于二极管桥的检测电路，采用负反馈的方法，将非线性误差从7.27%降低到0.662%。因此采用该种电路补偿方法，当预张力为50 MPa时，可获得较好的线性度与灵敏度。

为保证电容薄膜真空规能正常工作，必须考虑Inconel 600感压膜片在量程内允许最大负载情况下的强度，因此通过COMSOL软件计算膜片在受压情况下的应力分布情况。图5是预张力为70 MPa，气压为1 330 Pa下感压膜片的应力分布情况。

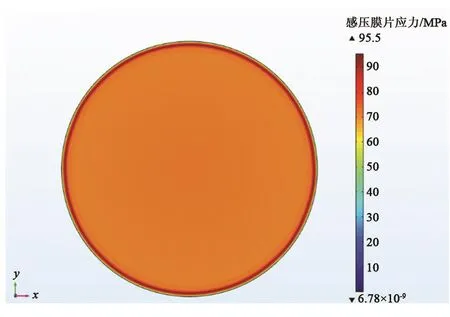
图5 量程内允许最大负载情况下感压膜片应力分布图Fig.5 Stress distribution under the maximum load allowed in the range

图5结果显示，最大应力分布在薄膜边缘，最大应力值为95.5 MPa，而Inconel 600合金的屈服强度为240 MPa，能够满足工作要求。

4 结论

本文以电容薄膜真空规电容感应模块为研究对象，建立了预张力薄膜挠度及电容感应模块输出电容的理论模型，选用COMSOL软件中特有的机电模块进行了模拟仿真，得到不同预张力条件下，真空规输出电容及感压膜片中心挠度随压力的变化关系，仿真结果与理论结果基本相符，COMSOL软件能对不同预张力薄膜的挠度及输出电容进行有效分析，为后续薄膜的设计提供了参考。预张力对真空规的输出特性影响明显，预张力一定时，输出电容随待测压力的增大而增大；随预张力的增大，输出电容减小，真空规的线性度提高，但灵敏度会随之降低，可见电容薄膜真空规的线性度与灵敏度相矛盾。在后续设计安装时，在满足强度要求下，设计者必须合理控制感压膜片预张力的大小，平衡线性度与灵敏度两者的关系。